单金属密封间隙两相流动及密封性能研究

张敏佳 ,马 艺,2* ,孟祥铠,2 ,彭旭东,2 ,王玉明

(1.浙江工业大学 机械工程学院,浙江 杭州 310023;2.浙江工业大学 过程装备及其再制造教育部工程研究中心,浙江 杭州 310023)

单金属密封作为牙轮钻头常用密封形式之一，具有耐高温、耐磨损和抗振动等特点，对钻头轴承系统起到了良好的保护作用.井下工作时，单金属密封面临着高温高压、频繁振动和复杂多相环境等恶劣工况，其使用寿命受到严峻挑战，尤其是受外界稠密多相流环境影响，携带高浓度固体颗粒的钻井泥浆极易侵入密封端面，加速端面磨损，进一步造成密封失效和钻头破坏[1-2].因此有必要开展多相环境下单金属密封端面微流场及密封性能研究.

目前，国内外针对金属密封已开展相关理论、模拟和试验研究.Xiong等[3]建立第一代单金属密封(SEMS)稳态数值模型，研究膜厚、液膜压力和泄漏率等密封参数的变化规律；Carre等[4]和Grimes等[5]结合国外钻井案例对比分析了第一代单金属密封(SEMS)和第二代单金属密封(SEMS2)的结构特点及性能差异；张毅等[6-7]利用有限元法分析了SEMS2端面接触应力分布和磨损形貌，针对高压工况进行了结构参数优化设计；Zhou等[8]、Huang等[9]和Zhang等[10]研究了双金属密封(DMES)中橡胶圈的应力分布及磨损规律；马艺等[11-12]和陈宇涛[13]建立SMES2热流固耦合数值模型，考察多场作用下密封端面变形规律和混合润滑机理，并进一步研究了振动工况下液膜形状及性能演变规律.总体来说，单金属密封的研究主要集中于端面热力变形、多场耦合作用及结构参数优化，尚未有单金属密封端面间隙两相流体流动特性的相关研究.部分学者针对机械密封两相流动的研究可为单金属密封间隙微流场分析提供一定的参考，如彭旭东等[14-15]分别开展了机械密封端面气液两相和固液两相流的研究，分析了端面流动特征及磨损状态；李世聪等[16]和李双喜等[17]基于动压型机械密封油气两相热流固耦合模型，考察了不同工况下动态密封性能的变化规律；Salant等[18]、Blasbalg等[19]、Wang等[20]和杨笑等[21]提出考虑相变和空化的机械密封两相数值模型，预测了两相密封对轴向扰动的瞬态响应；陈汇龙等[22]对液固两相工况下机械密封端面特征及沉积状态开展了相关研究.但上述研究方法并不完全适用于单金属密封特有的变压振动工况及润滑油-钻井泥浆的双腔多相工作环境.

本文中基于单金属密封热流固耦合数值模拟结果，建立单金属密封端面三维非均一液膜模型，采用Fluent软件模拟两相条件下单金属密封微流场特性及密封性能，分析不同环境压力和转速下密封间隙液膜压力、泥浆体积分布、泄漏率和摩擦力等性能参数的演化规律，并在此基础上，联合用户自定义函数和动网格技术，进一步研究周期性振动条件下单金属密封间隙动态流场特性，探讨振动工况对密封界面泥浆侵入特性的影响机理，为高可靠性钻头轴承金属密封系统的设计与开发提供理论依据.

1 模型建立及条件设置

1.1 几何模型

单金属密封结构主要包括金属动环、金属静环、O形橡胶圈和橡胶支撑垫，如图1所示.井下工作时，单金属密封的内径侧介质为润滑油，外径侧介质为钻井泥浆.金属动环随主轴转动，由于弹性元件和流体介质压力所形成的闭合力与端面液膜开启力的作用，静环与动环端面形成微米级润滑油膜，以阻止润滑油泄漏和钻井泥浆侵入轴承区域.

Fig.1 Structure of single metal seals 图1 单金属密封结构示意图

结合多场耦合数值计算结果[11]，建立多个不同工况对应的单金属密封非均一三维液膜模型.为提高计算效率，考虑到单金属密封间隙流体膜厚沿周向具有一致性，选取密封间隙的十八分之一(20°)作为本文中的计算域.计算域沿径向方向分为楔角区Ⅰ (29 mm≤r<31 mm)、密封区Ⅱ (31 mm≤r<34.3 mm)和倒角区Ⅲ (34.3 mm≤r≤34.5 mm)，以充分考虑钻井泥浆侵入密封端面间隙的过程.单金属密封主要结构参数和工况参数列于表1中.

表1 单金属密封结构和工况参数Table 1 Structural and operating parameters of single metal seals

1.2 湍流模型和两相流模型

为简化单金属密封液膜模型，作如下假设：(1)密封间隙具有连续性；(2)两相流体互不相容，均为不可压缩的均质流体，密度恒定；(3)忽略压力对流体黏度的影响；(4)不考虑金属密封环与液膜的滑移问题.

由于存在压差和动静环间相对运动，密封间隙流体运动呈压差剪切流形式.采用流动因子ε[23]判断密封间隙流体流动状态，计算得到 ε<1，即理论上密封间隙流体应处于层流状态.但由于内外径侧楔角与倒角的渐变结构特征，两处容易出现涡旋等湍流特征，并可能对密封区Ⅱ产生影响.另一方面，在计算所涉及工况的模型中，相对粗糙度最低可达到8.3%，对密封间隙内流体流动的影响不容忽视[24].因此，综合上述考虑，采用标准k-ω湍流模型计算单金属密封间隙流体域的压力场和速度场.该模型考虑低雷诺数及剪切流修正，对存在逆压梯度的流动求解精度较高，同时考虑分离与转捩[25].

因两相流体互不相容，采用基于欧拉-欧拉法的表面跟踪模型—Volume of Fluid模型(VOF).VOF模型通过求解单一的动量方程并跟踪，能够较好得到两相流体间的交界面，在液-液两相流动方面已经得到了成熟的应用[26-27].该模型中不同流体组分共用一套动量方程，所涉及的控制方程除该方程外还有质量守恒方程和物性方程，具体方程如下所示[28]：

式中：u为流体速度；ρm为混合流体密度；▽为哈密顿算子；p为流体压力；μm为混合流体动力黏度；g为重力加速度；FSV为表面张力等价体积力；F为相函数；Φ代指流体黏度等物性参数.

润滑油的黏度μoil采用黏温方程表示[29]：

式中：T0为参考温度；μoil-0为参考温度T0下的润滑油黏度；λ为黏温系数.

钻井泥浆是由水、膨润土和各种固体颗粒等形成的高分散体系，可视为伪均质流[30]，其黏度μmud采用API石油协会推荐形式[31]：

式中：T0为参考温度；μmud-0为参考温度T0下的钻井泥浆黏度；k为温度系数.

选取参考环境压力po=69 MPa，对应参考温度T0=180 ℃，两相流体物性参数为润滑油黏度μoil-0=0.0016 Pa·s，泥浆黏度μmud-0=0.0227 Pa·s，润滑油密度ρoil=861 kg/m3，泥浆密度ρmud=1742 kg/m3.

1.3 网格划分及边界条件

采用ICEM软件对单金属密封计算域进行六面体网格划分，边界条件设置如图2所示.进口压力pi为密封环内侧润滑油压力，出口压力po为外部钻井泥浆所处环境压力，动环端面设置转速为n的旋转壁面.VOF模型参数设置为第一相为密度ρoil和黏度μoil的润滑油，第二相为密度ρmud和黏度μmud的钻井泥浆，进、出口处钻井泥浆的体积分数分别为0和100%.

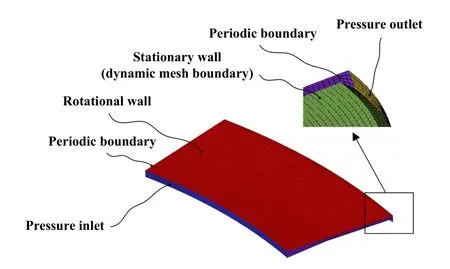
Fig.2 Boundary conditions of calculation domain for single metal seals 图2 单金属密封计算域边界条件

根据钻头振动形式[32]，动态计算时将静环端面设置为具有位移振幅为A、振动频率为f的正弦形式的运动壁面，施加轴向振动形式为xy=Asin(2πf·t).选取基于网格比例的分层模型(Dynamic layering)作为动态网格的更新方法.

1.4 求解流程和算法设置

给定结构参数和操作工况参数，根据单金属密封热-流-固多场耦合计算结果，构建单金属密封间隙流体域模型并划分网格.在Fluent软件中设置计算模型和边界条件后进行初始化赋值，通过求解相应控制方程得到单金属密封间隙稳态两相流场分布.在稳态基础上使用用户自定义函数(UDF)与动网格技术模拟静环的轴向周期性振动.使用SIMPLEC算法进行压力速度耦合，梯度计算采用Least squares cell based，压力插值选用Body force weighted.

2 网格无关性及方法准确性验证

2.1 网格无关性验证

在一定工况条件下(po=69 MPa、Δp=0.5 MPa、n=200 r/min、σ=0.1 μm)，选取不同网格数的模型开展单金属密封计算域的网格无关性验证.不同网格数量时密封间隙内润滑油泄漏率Q和密封间隙内总泥浆体积Vmud的变化规律如图3所示.由图3可以看出，随着网格数量由3.7 W增加至121.1 W，单金属密封的泄漏率和泥浆体积变化幅度逐渐降低.当网格数达到35 W时，单金属密封泄漏率和泥浆体积的变化率分别小于1.4%和0.6%.综合考虑计算精度与计算时间，选取网格数为35 W、尺寸为0.04 mm的计算模型来开展后续单金属密封间隙两相流动的模拟研究.

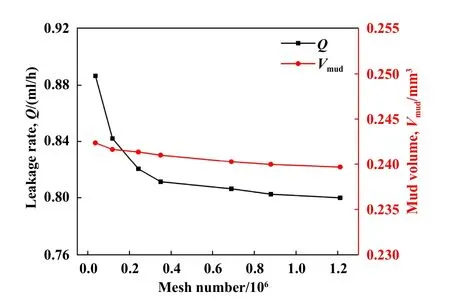
Fig.3 Verification of grid independence of calculation domain 图3 计算域网格无关性验证

2.2 计算方法准确性验证

为验证本文中计算方法的准确性，在相同工况参数、三种不同环境压力下，计算单金属密封间隙液膜压力径向分布，并与文献[11]结果进行对比，如图4所示.由图4可以看到，三种不同环境压力下密封区液膜压力的变化趋势与文献所得趋势一致，数值基本吻合，两者的最大偏差不超过0.05%.

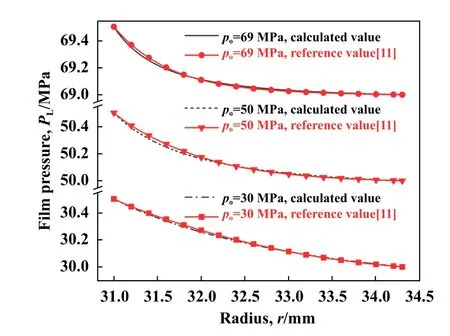
Fig.4 Comparison of film pressure of single metal seals between calculated values and reference values[11] 图4 单金属密封液膜压力计算值与文献值[11]对比

3 结果分析与讨论

3.1 密封间隙两相流动特征及密封性能

3.1.1 液膜压差及泥浆侵入特性

图5所示为不同环境压力po下单金属密封间隙内液膜压差与泥浆体积分数的曲线图.图6所示为不同环境压力po下密封区Ⅱ的液膜压差和泥浆体积分数分布云图.由图5可知，在整个密封间隙内，楔角区Ⅰ和倒角区Ⅲ的液膜压力pL分别与润滑油压力pi和泥浆压力po保持一致，密封区Ⅱ内液膜压差(pL-po)沿径向逐渐下降.随着环境压力po的增大，密封区Ⅱ同一径向位置的液膜压差不断减小，液膜压差曲线由近似线性变化变为斜凹型.分析原因主要是因为环境压力改变使得O形圈形态和端面液膜均发生变化.当环境压力由3 MPa增加至30 MPa之后，钻井泥浆压力克服O形圈对静环的支撑作用，静环受力方向和端面液膜状态发生了改变.

由图5所示泥浆体积变化可以看出，稳态条件下泥浆能够侵入密封区Ⅱ外侧和倒角区Ⅲ.这主要与动环旋转产生的剪切流动有关.结合图5(b)倒角区流线细节图可知，由于倒角结构和两相流体间相对运动的存在，倒角区内流体流动形成涡旋，使得外径侧泥浆具有一定速度从而进入密封间隙内.当动环转速为零时，密封间隙内流体流动仅为压差流动，外径侧泥浆无法侵入相对高压的密封区；当动环施加转速后，流体流动改为压差剪切流动.在动环旋转带动下，外径侧泥浆克服压差侵入到相对高压的密封端面.同时，泥浆侵入区域呈“喇叭口”型分布，泥浆体积分数αm沿膜厚方向先增大后减小.以环境压力po=69 MPa下密封区Ⅱ和倒角区Ⅲ的交界点r=34.3 mm为例，泥浆体积分数的变化幅度可达18.3%.这是因为越靠近动环端面，泥浆获得的流体旋转速度越大，越容易侵入密封区.而在靠近动环壁面区，泥浆体积分数受黏性阻碍作用存在一定下降.

由图6可以看出，随着环境压力po和对应环境温度的增加，受金属动、静环热力变形影响，密封区液膜由收敛型变为发散型，在环境压力po=69 MPa时，密封区膜厚沿径向变化梯度尤为明显，在外径侧增至0.90 μm.当环境压力po从3 MPa升高至69 MPa时，泥浆侵入半径由r=32.8 mm外扩至33.8 mm，密封区外径侧r=34.3 mm处的泥浆体积分数从95.4%降至68.3%.泥浆侵入密封间隙的程度随着环境压力增加而降低.这是因为当环境压力升高时，端面液膜平均膜厚增加，而且密封区内液膜压差整体下降，润滑油向外泄漏流动增强.另外，环境温度随之升高使得润滑油黏度大幅下降，流动产生的内摩擦力下降.在上述因素的共同影响下，高压环境下润滑油在密封间隙内的径向速度大幅增加，两相流体因相对运动产生的内摩擦力增加，泥浆侵入密封间隙的能力反而减弱.

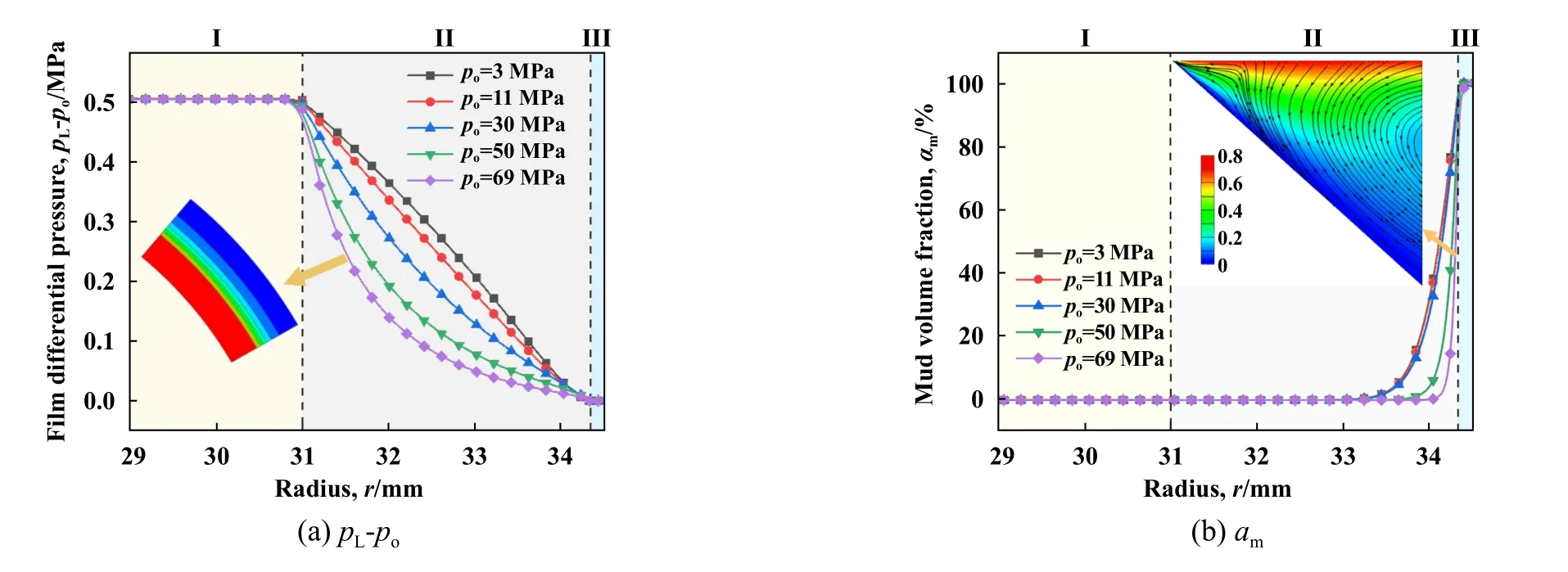
Fig.5 Radial distribution of film differential pressure and mud volume fraction in sealing gap under different environmental pressures (n=200 r/min)图5 不同环境压力下密封间隙液膜压差与泥浆体积分数径向分布(n=200 r/min)

图7所示为不同转速n下单金属密封间隙内液膜压差与泥浆体积分数曲线图.图8所示为不同转速n下密封区Ⅱ的液膜压差和泥浆体积分数分布云图.由图7可以看出，随着钻头转速n由200 r/min提高至1000 r/min，密封间隙内部液膜压差pL-po的变化趋势并不明显.结合图7放大图可知，靠内径侧液膜压力随转速升高而降低，外径侧液膜压力随转速升高而增加.这一现象主要与膜厚径向变化有关.由图8可知，当环境压力po=69 MPa时，端面膜厚沿径向方向逐渐增大，发散程度随转速增大而提高.在径向r≤32.4 mm区域内，受密封端面热变形占比增大影响，端面膜厚随转速增加而减小；在r>32.4 mm区域内，膜厚随转速升高而迅速增加.由于高速旋转使得内外侧温差增大，密封端面径向热变形梯度增大，使得液膜发散程度增加.当钻头转速n从200 r/min提高至1 000 r/min时，泥浆侵入密封端面的径向临界点从r=33.8 mm内移至33.1 mm，各径向位置处泥浆体积分数随转速升高而升高，密封区Ⅱ外侧r=34.3 mm处的泥浆体积分数从68.2%升高至87.5%.经统计，密封间隙内泥浆总体积随转速增加增幅1.2%.这是因为被涡旋带入的泥浆随动环转速的提高而具有更高的动能，更能克服逆压差流动的压差能和流动阻力，侵入高压密封端面的程度随之增强.

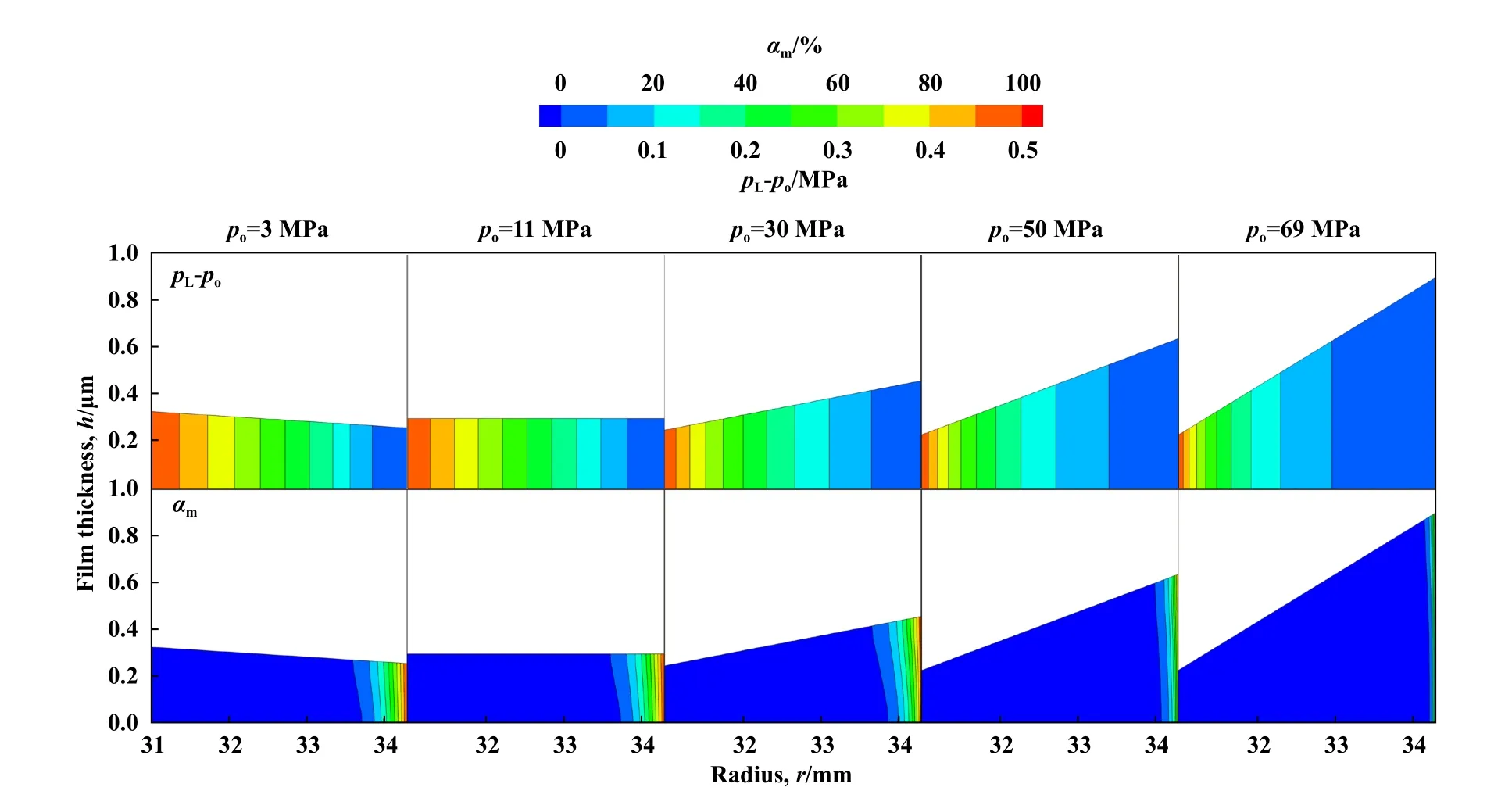
Fig.6 Distribution of film differential pressure and mud volume fraction in sealing area Ⅱ under different environmental pressures图6 不同环境压力下密封区Ⅱ液膜压差和泥浆体积分数分布云图(n=200 r/min)

Fig.7 Radial distribution of film differential pressure and mud volume fraction in sealing gap under different rotational speeds图7 不同转速下密封间隙液膜压差与泥浆体积分数径向分布(po=69 MPa)

3.1.2 两相环境下单金属密封性能

图9所示为不同环境压力po和转速n下单金属密封性能变化规律.由图9(a)可以看到，在转速一定时(n=200 r/min)，单金属密封泄漏率和液膜开启力均随环境压力的升高而增大，液膜摩擦力则刚好相反.当环境压力po从3 MPa提高至69 MPa时，泄漏率和开启力分别增至48.2倍和21.3倍，摩擦力降为0.6%.结合液膜特性及泥浆分布规律可知，环境压力po的增大伴随着对应地层温度的升高，密封端面间隙平均膜厚不断增加，且润滑油黏度降低.因此，单金属密封润滑油泄漏率的增长幅度显著，开启力受膜压影响也呈正相关增长趋势.另一方面，结合图6可知，高压环境下泥浆侵入密封间隙的程度减弱，而且环境温度随之升高使得润滑油黏度大幅下降，单金属密封的摩擦力进而逐渐变小.由图9(b)可知，在环境压力一定时(po=69 MPa)，当钻头转速n由200 r/min提高至1 000 r/min时，开启力基本不变，而单金属密封泄漏率和摩擦力分别增长了15.4%和4.6倍.这主要是因为转速变化对密封区Ⅱ的液膜压力影响较小，但对液膜平均膜厚和泥浆侵入程度影响显著.在该环境压力下，泥浆黏度大于润滑油黏度，因而混合流体黏度随转速升高而增加，造成密封端面摩擦力增大.

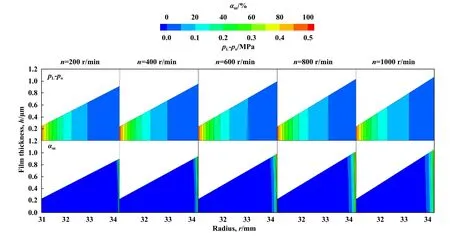
Fig.8 Distribution of film differential pressure and mud volume fraction in sealing area Ⅱ under different rotational speeds图8 不同转速下密封区Ⅱ液膜压差和泥浆体积分数分布云图(po=69 MPa)

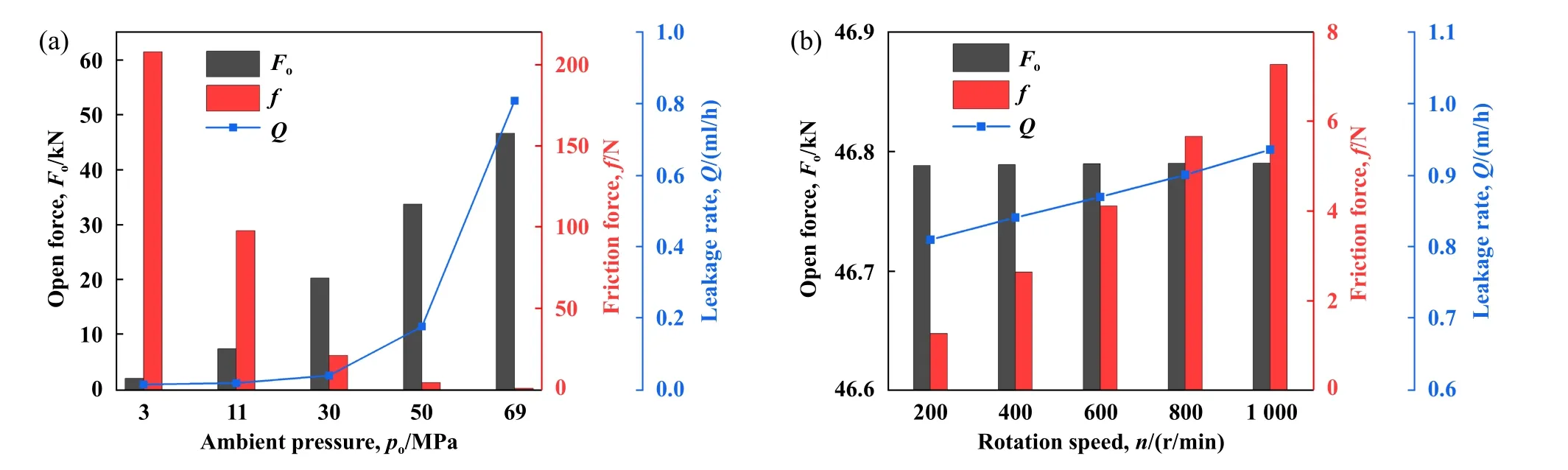
Fig.9 Variation of sealing performance of single metal seals under different environmental pressures and rotational speeds图9 不同环境压力和转速下单金属密封性能变化规律

3.2 振动工况下密封间隙流场及性能演化

图10所示为不同环境压力po和转速n下周期性振动对单金属密封间隙内泥浆体积分布的影响.由图10可以看到，周期性振动条件下泥浆侵入密封间隙内部的体积分数不断波动.在同一转速条件下(n=200 r/min)，当环境压力po≤30 MPa时，随着振动时间的增加，泥浆体积分数的周期性振动波型呈逐渐上升趋势，泥浆侵入密封区的径向临界点向内径侧移动愈发明显，即外部泥浆侵入区域随钻头工作时间的延长不断扩大，但变化过程相对缓慢.这使得泥浆逐渐在密封界面累积，极易导致密封端面磨损加剧，加速失效.当po>30 MPa时，泥浆体积分数波型基本保持一致，径向临界点变化不明显.这是因为当静环向动环靠近时，液膜压力因挤压作用增强而升高；当静环远离动环时，液膜压力因挤压作用减弱而降低，液膜压力的周期性变化导致泥浆体积分数随时间不断波动.在po≤30 MPa时，小膜厚下挤压效应强烈，液膜压力波动幅度较大，在密封区内交替形成高压区(pL>pi)和低压区(pL30 MPa时，大膜厚下液膜压力波动幅度较小，始终保持沿径向逐渐降低的规律，泥浆侵入与挤出行为处于动态平衡状态.在同一环境压力条件下(po=69 MPa)，随着转速n提高至1 000 r/min时，泥浆侵入区域和泥浆体积分数随振动时间的变化明显大于其他转速，泥浆体积分数振动波峰波谷均呈上升趋势，最终在动环高速旋转影响下，密封间隙内泥浆侵入量与挤出量短暂振荡后随时间延长逐渐平衡.

图11所示为不同环境压力po和转速n下周期性振动对单金属密封泄漏率和泥浆体积的影响.由图11可以看到，振动工况下泄漏率和泥浆体积的周期性波动形式相反.当环境压力po由3 MPa提高至69 MPa时，泄漏率呈整体增大趋势，且振幅由波动均值的57.4%降低到11.5%.这主要是由于密封区内液膜压力波动随环境压力增加而整体减弱，液膜压差振幅降低所致.在环境压力一定时(po=69 MPa)，随着转速的增加，泄漏率均值及最大振幅均增加，但在转速n=1000 r/min时泄漏率波动幅值随时间延长不断衰减.对于侵入密封间隙的泥浆体积来说，其均值随环境压力增加呈先升后降的变化趋势，泥浆体积随转速升高不断增加，而波动振幅随环境压力增加而逐渐增大，其受转速影响变化不大.这主要与不同工况下膜厚和泥浆侵入程度的差异有关.结合图6与图8可知，出现这种现象是因为在环境压力po≤30 MPa下，当受静环振动密封区存在低压(pLpo)，泥浆流动为逆压差流动，但由于密封端面液膜压力升高，侵入密封区的泥浆受压差影响开始向外流动，同时外径侧泥浆仍可受涡旋和剪切流动影响侵入密封区，只是侵入幅度下降.同一个周期内上述两个过程直接导致泥浆侵入和挤出量不同，进而在密封区内产生泥浆积累现象.当po>30 MPa时，泥浆侵入程度随环境压力增大快速衰减，泥浆侵入体积量总体减小，而在高压高转速(po=69 MPa、n=1000 r/min)条件下，随着泄漏率振动幅值逐渐下降，泥浆体积量不断累积，容易导致密封端面润滑状态恶化及泥浆侵入磨损加剧.

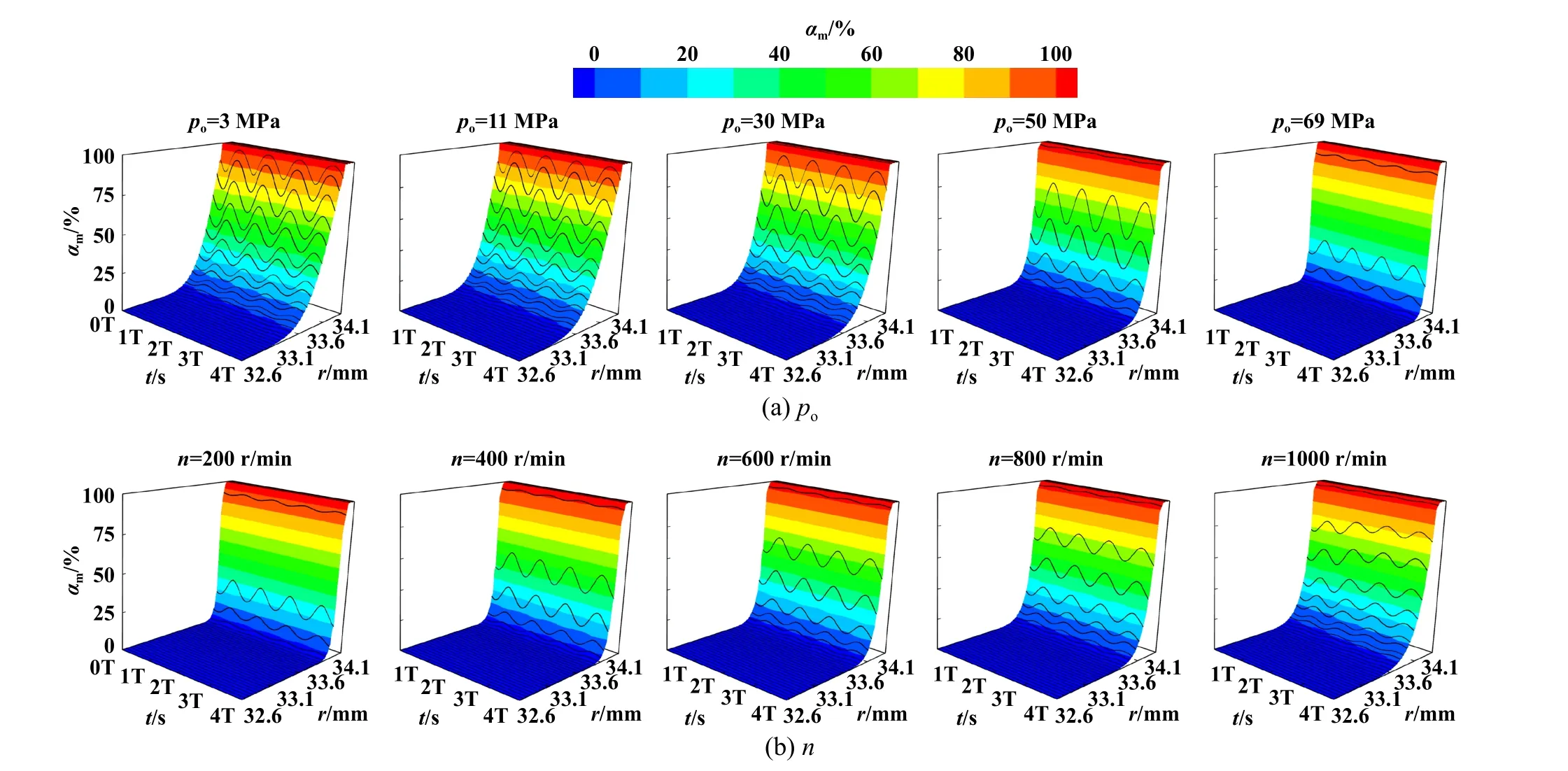
Fig.10 Influence of periodic vibration on mud volume distribution under different(a) environmental pressures and (b) rotational speeds图10 不同(a)环境压力和(b)转速下周期性振动对泥浆体积分布的影响

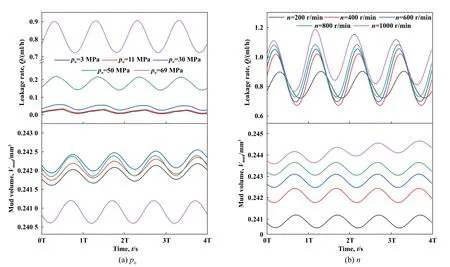
Fig.11 Dynamic changes of leakage rate and mud volume under different environmental pressures and rotational speeds 图11 不同(a)环境压力和(b)转速下周期性振动对泥浆体积分布的影响

图12所示为不同环境压力po和转速n下周期性振动对单金属密封液膜开启力和液膜摩擦力的影响.由图12可知，随着环境压力的增加，开启力均值增大而摩擦力均值降低，且两者的振幅均逐渐减小.当环境压力po从3 MPa增加至69 MPa时，开启力和摩擦力波动幅度分别由均值的2.1倍和3.3%几乎降为零.这是因为环境压力较低时振动挤压效应明显，密封区内液膜压差和体积分数波动剧烈，使得开启力和摩擦力振幅均较高.由图12可知，当环境压力po=3 MPa时，摩擦力波动曲线缓慢下降，结合图10可知，此时泥浆逐渐累积于密封界面，密封间隙混合黏度降低，从而使得摩擦力波峰略有减小.在同一环境压力(po=69 MPa)下，开启力均值与振幅随转速增加变化较小，而摩擦力均值和振幅均呈增长趋势.特别是在转速n=1000 r/min时，开启力的波峰和波谷值开始衰减，摩擦力的波峰和波谷值逐渐递增.这主要与密封界面泥浆累积和两相黏度变化有关，显然该现象对于密封间隙液膜的稳定保持是不利的.

4 结论

a.稳态工况下单金属密封端面泥浆侵入区域主要集中于密封区Ⅱ外侧和倒角区Ⅲ，侵入程度随环境压力升高和转速降低而减弱.在沿膜厚方向的速度梯度及涡旋作用下，动环端面外侧更易受泥浆侵入影响而发生磨损.

b.周期性振动过程中，较低环境压力(po≤30 MPa)下密封区泥浆侵入区域因动态挤压效应不断扩大且产生累积现象.

Fig.12 Dynamic changing regularity of opening force and friction force under different environmental pressures and rotation speeds图12 不同环境压力和转速下开启力和摩擦力动态变化规律

c.单金属密封稳态泄漏率随环境压力和转速增加而显著增加，液膜摩擦力随环境压力降低和转速增加而增大.周期性振动工况下摩擦力均值及振幅随环境压力增加而减小，随转速升高而增大.