复数中最值与范围解答策略

李佩荷

(山东省青岛西海岸新区第一高级中学)

复数中的最值问题主要是模的最值与参数的最值,常用以下几种方法求解.

1 利用二次函数的性质解题

即a2＝9－9b2.从而

故选B.

2 利用点在平面坐标系中的位置解题

A.(－∞,0)∪(1,＋∞) B.(0,1)

C.(－∞,－1)∪(1,＋∞) D.(－1,1)

在平面坐标系中,若点(a,b)在第一象限,则若点(a,b)在第二象限,则若点(a,b)在第三象限,则若点(a,b)在第四象限,则

3 利用三角形两边之和大于第三边的性质解题

当z1＝－1,z2＝1,z＝3时,有

此时|z|＝3,所以|z|max＝3,故选B.

4 利用圆的性质解题

则1≤|z－(－1－i)|≤,即复数z对应的点Z到点C(－1,－1)的距离d满足.设P(1,1),|z－1－i|表示复数z对应的点Z到点P(1,1)的距离,结合图1可知|z－1－i|的最大值为

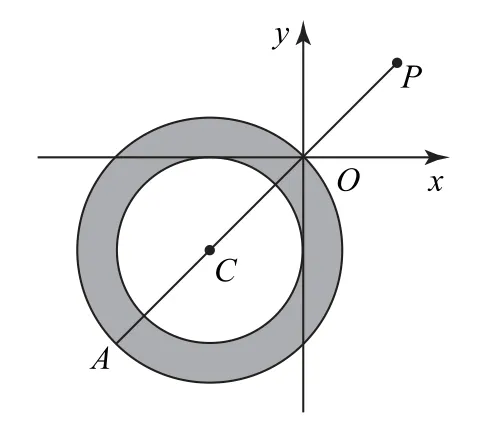
图1

5 利用三角函数的性质解题

A.3 B.4 C.5 D.6

由－1≤sin(φ－α)≤1,可得

则|z＋1|的最小值为3,故选A.

6 利用基本不等式解题

C.的最大值为2 D.没有最大值

7 利用|z1|－|z2|≤|z1±z2|≤|z1|＋|z2|解题

方法2因为z＋i＝(z－4＋5i)＋(4－4i),所以|4－4i|－|z－4＋5i|≤|z＋i|≤|4－4i|＋|z－4＋5i|,从而,故|z＋i|的取值范围为.

(完)