Fisher正则化的最小二乘孪生支持向量机
2023-03-11陈素根
张 萌,陈素根
(安庆师范大学 数理学院,安徽 安庆 246133)
20世纪90年代,VAPNIK等[1]提出了支持向量机(Support vector machine,SVM)算法,其是一种借助于统计与优化方法来解决机器学习问题的强有力工具[2],被广泛应用于分类和回归等各种实际问题中。然而,SVM具有较高的计算复杂度等问题,限制了它的实际应用。为了克服SVM存在的问题,人们开展了大量研究并提出了许多SVM 改进算法[3]。2006 年,MANGASARIAN 等提出了一种多平面近端支持向量机[4],该算法不仅有较低的计算复杂度,而且可以有效地解决异或问题。受其启发,JAYADEVA等提出了孪生支持向量机(Twin support vector machine,TWSVM),其仅仅求解两个规模较小的二次规划问题,且训练速度大约是传统SVM 的4 倍[5]。2009 年,KUMAR 等[6]在TWSVM 基础上提出了最小二乘形式的孪生支持向量机(Least squares twin support vector machine,LSTSVM),并利用等式约束代替TWSVM中的不等式约束,将问题转化为求解线性方程组,从而使得LSTSVM相对于TWSVM具有计算简单和训练速度快的优势。2011 年,陈小波等[7]提出了投影孪生支持向量机(Projection twin support vector machine,PTSVM),该算法寻找两个最优的投影方向以代替两个非平行平面。受PTSVM 启发,2012年邵元海等[8]提出了最小二乘形式的投影孪生支持向量机(Least squares projection twin support vector machine,LSPTSVM)。从此,非平行平面支持向量机算法被广泛研究,且取得了丰硕的研究成果[9-13]。
虽然LSTSVM具有较快的求解速度,但其在求解线性方程组过程中可能存在矩阵奇异问题。同时,训练过程会受每个训练样本影响,这使得其泛化性能较差。2018年,吴青等[14]对LSTSVM进行改进,并提出了最小二乘形式的大间隔孪生支持向量机(Least squares large margin twin support vector machine,LSLMTSVM),该算法在LSTSVM 的优化目标函数中引入间隔分布,提高了算法的泛化性能,但LSLMTSVM 仍存在参数选择困难等问题。为进一步提升LSTSVM 性能,受Fisher 正则化思想[15]的启发,本文提出了Fisher 正则化的最小二乘孪生支持向量机(Fisher regularized least squares twin support vector machine,FLSTSVM)。FLSTSVM 算法的优点有:(1)引入双Fisher 正则化项,增强获取判别信息的能力,提高了算法的泛化性能;(2)基于结构风险最小化原则,解决了求解过程中可能出现矩阵奇异的问题;(3)FLSTSVM具有相对较快的训练速度。
1 相关工作
考虑n维实数空间中的一个二分类问题,假设给定的训练集T={(,yj)|i=1,2,j=1,2,3,…,mi},其中,m1+m2=m,yj∈{+1,-1 }∈Rn表示第i类、第j个输入样本,A∈表示m1个n维的正类样本,B∈Rm2×n表示m2个n维的负类样本。
1.1 TWSVM
线性TWSVM寻找两个非平行的超平面fi(x)=+bi=0,i=1,2,使每一个超平面尽可能靠近一类样本点并且远离另一类样本点,其原始优化问题为
其中,c1>0,c2>0是惩罚参数,ξ1,ξ2是松弛变量,e1,e2是分量全为1的适当维数的向量。
引入拉格朗日函数,并利用KKT(Karush-Kuhn-Tucker)条件,将优化问题(1)和(2)转化为对偶形式:
其中,α和γ是拉格朗日乘子,求解公式(3)和(4),得到w1,b1,w2,b2。
对于任意x∈Rn,i=+1,-1,根据公式(5)进行分类:
这里 |· |表示数据点到超平面的垂直距离。对于非线性TWSVM,选择合适的核函数将原始数据映射到高维特征空间,类似于线性TWSVM构造非线性模型,可参见文献[5]。
1.2 LSTSVM
LSTSVM 也是寻找两个非平行超平面fi(x)=+bi=0,i=1,2,其是TWSVM 的一种改进算法。它基于平方损失函数,并利用等式约束代替不等式约束,线性LSTSVM的原始优化问题为
对于优化问题(6),将等式约束代入目标函数,关于w1和b1求偏导数且令其等于零,整理得
令E=[A e],F=[B e],化简可得
对于优化问题(7),同理可得
求得w1,b1,w2,b2后,可得超平面fi(x)=+bi=0,i=1,2。对于任意x∈Rn,i=+1,-1,根据公式(11)进行分类:
这里 |· |表示数据点到超平面的垂直距离。对于非线性的LSTSVM算法,可见参考文献[6]。
2 Fisher正则化的最小二乘孪生支持向量机
2.1 线性的FLSTSVM
为了提高LSTSVM的判别能力,本文引入双Fisher正则化项对LSTSVM进行改进。Fisher正则化的最小二乘孪生支持向量机也寻找两个非平行的超平面:
给定正类样本对应的矩阵A和负类样本对应的矩阵B,记
正类Fisher正则化项[15]定义如
负类Fisher正则化项[15]定义如
正类Fisher正则化项和负类Fisher正则化项统称为双Fisher正则化项,其中公式(15)和(16)中的第一项为相应的类内散度,第二项是相应的类间散度。
于是,对于给定的训练样本集,考虑如下两个优化问题:
其中,c1,c4>0表示正则化参数。公式(17)式和(18)的目标函数中第一项是样本点到相应类的超平面距离平方和,最小化这一项可使这一类样本点聚集在此超平面周围。目标函数的第二项为双Fisher正则化项,最小化这一项可使类内散度最小化和类间散度最大化。然而,优化问题(17)和(18)是非凸的,不易求解。因此,对优化问题(17)和(18)的目标函数和约束条件进行改进,同时在目标函数中引入新的正则项以实现结构风险最小化原则。于是,线性FLSTSVM原始优化问题为
其中,c1,c2,c3,c4,c5,c6>0为参数,ξ1,ξ2表示松弛变量,e1,e2是分量全为1的适当维数的向量。
对于优化问题(20),将等式约束代入目标函数以得到无约束问题:
由公式(25)和(28)求得w1,b1,w2,b2后,可得超平面(12)。对于任意x∈Rn,i=+1,-1,根据公式(29)进行分类:
综上分析,本文给出了线性FLSTSVM的算法步骤。
2.2 非线性FLSTSVM
将线性FLSTSVM扩展为非线性模型,对于非线性情况,首先令C=[A;B],选择合适的核函数K,寻找两个非平行超曲面:
与线性情况类似,分别记
类似于线性情况,非线性FLSTSVM的原始优化问题如
类似于线性FLSTSVM 的求解过程,将等式约束代入目标函数以转化为无约束问题,并分别关于wi,bi(i=1,2)求导,经过一系列化简,求得
求解公式(37)和(38),可得
由公式(39)和(40)求得w1,b1,w2,b2后,可得两个非平行超曲面,如公式(30)。于是,对于任意测试样本x∈Rn,i=+1,-1,根据公式(41)进行分类:
非线性FLSTSVM算法的求解过程与线性FLSTSVM算法非常相似,唯一不同的是先选择合适的核函数K,并将数据映射到高维空间。
3 实验结果与分析
为验证本文所提FLSTSVM算法的有效性,在2个人工数据集和9个UCI数据集上开展实验,并分别与TWSVM[5]、LSTSVM[6]、PTSVM[7]、LSPTSVM[8]和LSLMTSVM[13]对比。实验均以MATLAB R2016a 为环境,硬件配置为Windows10操作系统,6 GB内存的计算机。在实验过程中,使用逐次超松弛技术来求解各算法中的二次规划问题。对于非线性算法,核函数选择RBF 核K(x,y)=,μ为核参数。最优参数均采用10-折交叉验证和网格搜索的方法进行选择,参数都取自集合{2i|i=-8,-7,-6,…,8 }。每个实验重复10次,并将实验结果的平均值和方差作为最后结果。
3.1 人工数据集
在两个人工数据集XOR和复杂XOR数据集上进行实验,其中,XOR包含240个样本(120个正类样本和120 个负类样本),而复杂XOR 包含172 个样本(90 个正类样本和82 个负类样本)。图1 给出了XOR和复杂XOR数据集的散点分布。图2给出了本文所提线性FLSTSVM算法在两个数据集上的分类效果。不难发现,线性FLSTSVM算法能够较好地解决XOR和复杂XOR数据分类问题。同时,表1给出了各线性算法在XOR和复杂XOR数据集上的实验结果,并用粗体表示最好的分类结果。
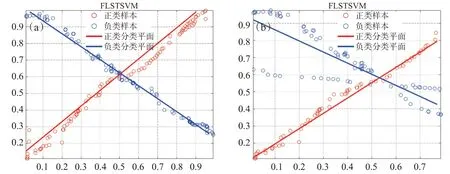
图2 线性FLSTSVM算法在XOR和复杂XOR数据集上的分类效果。(a)XOR数据集;(b)复杂XOR数据集

表1 线性算法在XOR和复杂XOR数据集上的分类结果
从表1可看出,本文算法在XOR和复杂XOR数据集上均取得了最好的分类准确率,故验证了算法的有效性。需要指出的是,与其他算法相比,虽然FLSTSVM分类准确率都是最好的,但并不能明显提高分类准确率,这可能是因为在XOR和复杂XOR数据集上非平行平面孪生支持向量机算法都具有相对较好的性能。另外,实验中的复杂XOR数据集规模不大,FLSTSVM算法增强获取判别信息的能力没有得到充分体现。
3.2 UCI数据集
为了进一步验证算法有效性,本文在UCI 数据集上进行实验,并分别与TWSVM、LSTSVM、PTSVM、LSPTSVM 和LSLMTSVM算法进行比较,表2和3分别给出了线性和非线性算法实验结果。可以看出,本文所提出的FLSTSVM算法在大部分数据集上都取得了较好的分类准确率,验证了该算法的有效性。在表2 可以发现,线性FLSTSVM 算法在大多数数据集上的准确率要优于其它算法。例如,在Votes数据集上,线性FLSTSVM准确率为96.39%,而TWSVM为95.86%,LSTSVM为95.86%,PTSVM为95.73%,LSPTSVM为95.97%,LSLMTSVM为95.19%。表3结果与表2相似,验证了非线性算法的有效性。例如,在Breast数据集上,非线性FLSTSVM的分类准确率为77.98%,比TWSVM高1.15%,比LSTSVM高0.47%,比PTSVM高1.09%,比LSPTSVM高0.87%,比LSLMTSVM高0.76%。另外,表2和3的最后一行用“W-T-L”(win-tie-loss)比较了FLSTSVM与其他算法的分类准确率。可以看出,在大部分情况下,FLSTSVM有较高的分类准确率。在线性情况下,FLSTSVM仅仅比LSMTSVM的性能稍微差一点,“W-T-L”的结果为4-0-5;在非线性情况下,FLSTSVM与所有算法的“W-T-L”比较结果都要好一点。

表2 各线性算法在UCI数据集上的分类结果
图3和4分别给出了在线性和非线性情况下各算法运行一次的时间图,可以发现FLSTSVM在大部分情况下都有较快的训练速度,仅比LSTSVM 运行时间长,比其他算法的运行时间都短,进一步验证了本文所提算法的有效性。实际上,本文所提FLSTSVM 算法是在LSTSVM算法的基础上引入了Fisher正则化项,求解过程与LSTSVM 相似,但是在具体计算过程中需要多计算一些矩阵乘法运算。相较其它算法,TWSVM 和PTSVM需要求解二次规划问题,求解速度要慢一点;同时LSPTSVM 和LSLMTSVM虽然也是求解线性方程组问题,但都需要进行一系列矩阵乘法运算。

图3 线性算法在UCI数据集上的运行时间
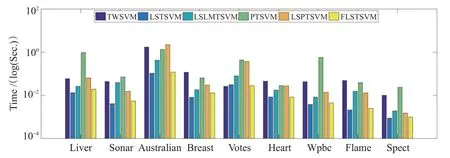
图4 非线性算法在UCI数据集上的运行时间
4 结束语
本文基于双Fisher正则化项提出了一种新的最小二乘孪生支持向量机分类算法,有效提升了算法获取判别信息的能力。同时,该算法是基于结构风险最小化原则,克服了LSTSVM求解过程中可能出现的矩阵奇异问题。在人工数据集和UCI 数据集上验证了本文所提FLSTSVM 算法的有效性,结果显示FLSTSVM 算法在大多数数据集上具有较高的分类准确率和相对较快的训练速度。将FLSTSVM 算法推广到多类分类和半监督分类可作为今后的研究。
