基于遗传算法的腔体滤波器耦合参数提取

王 鹏，宋娅雯，潘 盼，段凯月，黄立场，章 曼，靳宝坤

（1.安庆师范大学 电子工程与智能制造学院 安徽 安庆 246133；2.安徽大学 计算智能与信号处理教育部重点实验室，安徽 合肥 230601）

当前环境中频谱资源日益拥挤，伴随着各种噪声以及不同频段之间的干扰，高性能的微波滤波器的需求量不断增加。随着5G时代的到来，无源器件的发展也在面临着诸多挑战，如追求小型化、高选择性、带外抑制能力等方面。腔体滤波器是无线通信基站和卫星通信系统的关键器件，被广泛应用于卫星系统和无线通信系统的射频前端，其性能直接影响着通信质量[1-3]。由于材料特性的变化和加工生产的误差，滤波器的性能可能会发生变化，因此对滤波器的调试必不可少，随着大批量生产的开展，以往利用人工调节螺杆来进行调试的高度专业化导致工作效率低下，成本增加。基于以上原因，本文通过提取交叉耦合腔体滤波器的耦合参数来加速滤波器的调优过程。

交叉耦合腔体滤波器的耦合参数至关重要，从良好谐振状态或严重失调状态提取与滤波器频率响应相对应的耦合矩阵对快速辅助调试会产生显著影响。提取不同状态下的耦合矩阵，并比较其与目标矩阵在相同拓扑结构下的差异，可以更好地帮助技术人员确定调试的方向与幅度[4-7]。

很多学者针对耦合矩阵提取方法开展了研究。蒋廷利等在研究过程中引入了遗传算法，基于该方法对初始数据进行处理，并在去除相位加载后拟合Y参数来得到所需的耦合矩阵[8]。WANG等[9]通过全局优化与矢量拟合相结合的方式来有效消除了由于滤波器的输入输出端口负载传输线引起的模拟或实测Y参数的相移效应。尽管此类方法可以达到一定效果，但是这些方法对于变量的个数以及目标参数的要求高，依赖于多种算法或者参数组合，增大了应用难度。WANG等[10]成功得到了Y参数的特征多项式，并采用柯西法，利用复数极点以及Y参数的残差，得到了对应实际的滤波器物理耦合拓扑结构所需的CM以及每个谐振腔的空Q。李里[11]深入研究了滤波器无载Q值过时提取精度不佳的问题，并通过柯西预处理方法进行优化，运用MATLAB GUI平台设计了机辅系统。然而，柯西法同样存在缺陷，其取样点必须在通带附近，否则会带来二阶效应，且在高阶时容易产生病态矩阵。

本文首先运用遗传算法拟合得到滤波器最优传输零点位置，再对耦合矩阵非零值进一步确定以得到耦合矩阵的目标函数。采用该方法对腔体滤波器实测数据进行参数提取，结果发现S参数曲线结果吻合良好，验证了方法的有效性。通过比较理想耦合矩阵与实际耦合矩阵，可以指导滤波器的快速调试。

1 拟合传输零点

滤波器可以看成二端口网络，其中反射系数S11、传输系数S21可描述为[12]

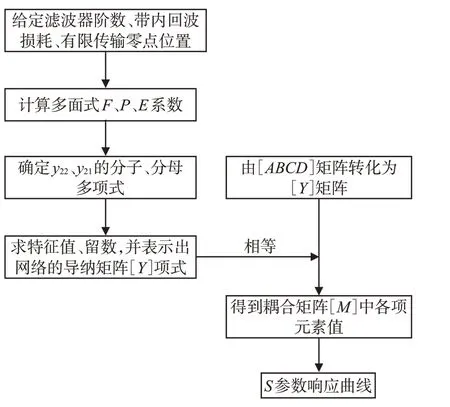
图1 滤波器耦合矩阵综合流程

2 最终耦合矩阵

基于上述过程得到了传输零点位置，再加上滤波器阶数等信息，即可实现对S参数的提取。然后，执行迭代过程，基于Fobj取值可以确定goals_S和S参数的一致性，如果其值较小，则意味着二者的一致性程度较高，此时根据适应度最小值即可确定有限传输零点。该方式得到的耦合矩阵M0仍然难以满足准确性的要求。对此可继续进行处理，以M0为辅助矩阵，并通过遗传算法进行计算，由此得到最终的耦合矩阵。具体采用N+2型耦合矩阵，对应的元素数目可达到(N+2)2，所以通过遗传算法计算需要花费较多时间，难以满足效率要求。为了解决上述问题，可对矩阵内的非零元素位置进行确定，从而有助于提升目标函数收敛性。对矩阵元素进行遍历，通过for 循环，检索出满足精度要求的非零元素。M、count分别是矩阵维度、非零元素数目。通过deta间接表示非零元素值，根据求解结果以确定最佳deta值，在此基础上进一步得到各个非零元素值。实现该功能的关键代码见图2，整个方法见图3。

图2 确定最终耦合矩阵关键代码

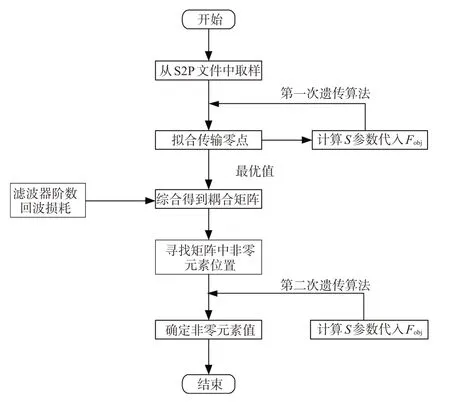
图3 基于遗传算法的参数提取流程

3 微波腔体滤波器耦合参数提取应用实例

针对微波腔体滤波器的耦合参数提取的不同策略，以六阶对称传输零点的交叉耦合带通滤波器和9阶3零点交叉耦合滤波器为例，通过矢量网络分析仪对滤波器的S参数特征数据进行采集，提取了不同状态下的耦合矩阵并得到实际耦合矩阵，通过比较提取的耦合矩阵和目标矩阵在相同拓扑结构下的差异，验证S参数曲线结果是否吻合良好，从而判断该方法的有效性并指导滤波器的快速调试。

3.1 六阶交叉耦合带通滤波器耦合参数提取

该部分采用六阶对称传输零点的交叉耦合带通滤波器来验证本文方法的有效性。该滤波器采用CT型拓扑结构，其参数指标要求：滤波器带宽为200 MHz，中心频率为5 200 MHz，带外有限传输零点为5 076.5 MHz 和5 326.5 MHz。为了获得本文方法的有效性，首先分析了文献[9]中所提方法的有效性。表1是S参数特征多项式的计算结果，表2是利用S参数特征多项式提取的耦合矩阵。表2与表3的计算结果基本一致，其中表3是采用CST Filter Designer软件得到的计算结果。显然，表2的实验结果验证了文献[9]所提方法的可靠性和准确性，保障了在完成耦合参数提取后的后续工作。由分析可知，文献[9]所提方法也具有一定的局限性。这是由于每个谐振腔都与源和负载之间存在着耦合，这在实际的滤波器物理结构中是没有办法实现的，所以需要后续对耦合矩阵进行转换，方可实现物理结构的耦合矩阵。本文所提算法获得的耦合矩阵如表4所示。

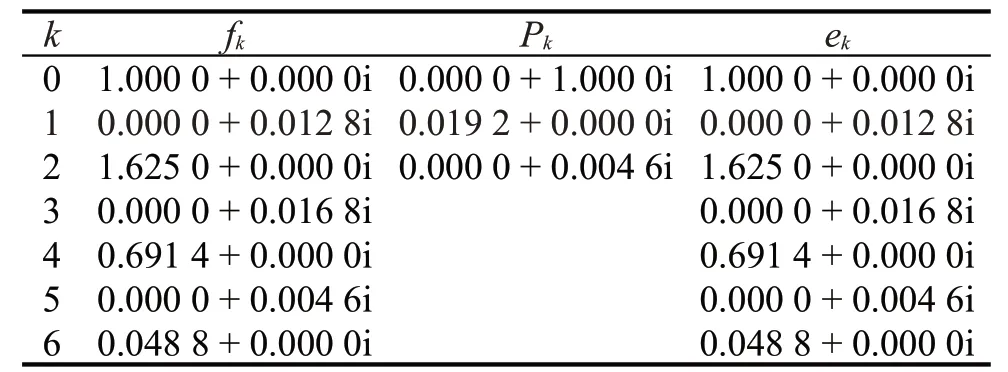
表1 六阶腔体滤波器归一化特征多项式系数

表2 初始耦合矩阵

表3 CST Filter Designer软件计算结果

表4 最终提取的耦合矩阵

提取的S参数如图4所示，可见满足滤波器200 MHz带宽和中心频率为5 200 MHz的要求。滤波器群时延曲线如图5所示，通带内群时延和幅度基本一致，保证了输出信号失真度不超过允许范围。对应单腔频率（MHz）为[5 314.755 2,5 081.127 7，5 088.690 7，5 306.609 9，5 152.962 2，5 243.500 5]。从上面数据分析可知，本文所提方法在耦合滤波器参数提取效率方面明显优于文献[9]所提方法。

图4 读取S参数

图5 群时延

3.2 九阶交叉耦合滤波器耦合参数提取

为了进一步验证本文所提方法的性能，采用交叉耦合滤波器（9阶3零点）来进行实验验证。图6为交叉耦合滤波器S参数采集平台，可实时采集本文所提算法的耦合参数。采用矢量网络分析仪（VNA）对交叉耦合滤波器（9阶3零点）进行S参数的实时采集，通过实时数据采集程序得到S2P 文件。该滤波器采用Floded 折叠型拓扑结构，通过读取S2P 文件可以判断出滤波器的带宽为74 MHz、中心频率为924 MHz。选取滤波器的9个点所对应的单腔频率分布见表5。

表5 滤波器单腔频率/MHZ

图6 交叉耦合滤波器S参数实时采集

图7 是拟合传输零点后的S曲线，可知，本文方法提取的理论参数S11曲线下部峰值保持齐平，幅度为-25 dB，符合切比雪夫滤波器的波纹特性；拟合出的最优传输零点在[-1.435 7,-1.296 2,-1.233 8]，三个零点与读取数据基本吻合，从而验证了所提方法的有效性。

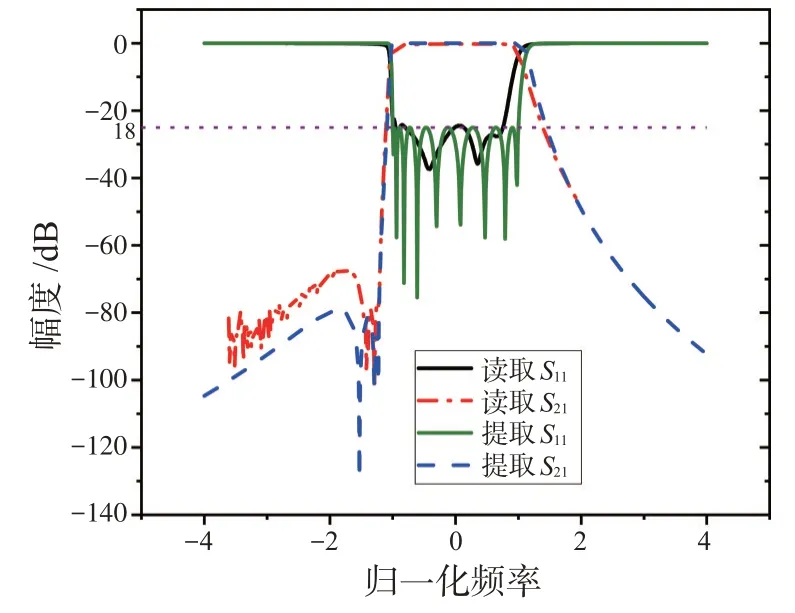
图7 拟合传输零点后S曲线

图8是拟合的最终响应曲线，可以看出，S11、S21在幅度上基本一致；在低频处存在一定差异，其主要原因是由于噪声干扰，而且传输零点又十分接近。图9给出了该滤波器群的时延曲线，可以看出，该滤波器群时延最高约为230 ns，其值在可控范围内，较好满足了相位不失真条件。表6是理想耦合矩阵，表7是最终提取的耦合矩阵，对比数据可知，最终提取的耦合矩阵非常接近理想耦合矩阵，因此本文方法提取的耦合矩阵可使滤波器获得良好的性能。同时，最终提取的耦合矩阵可以指导滤波器的辅助调试。

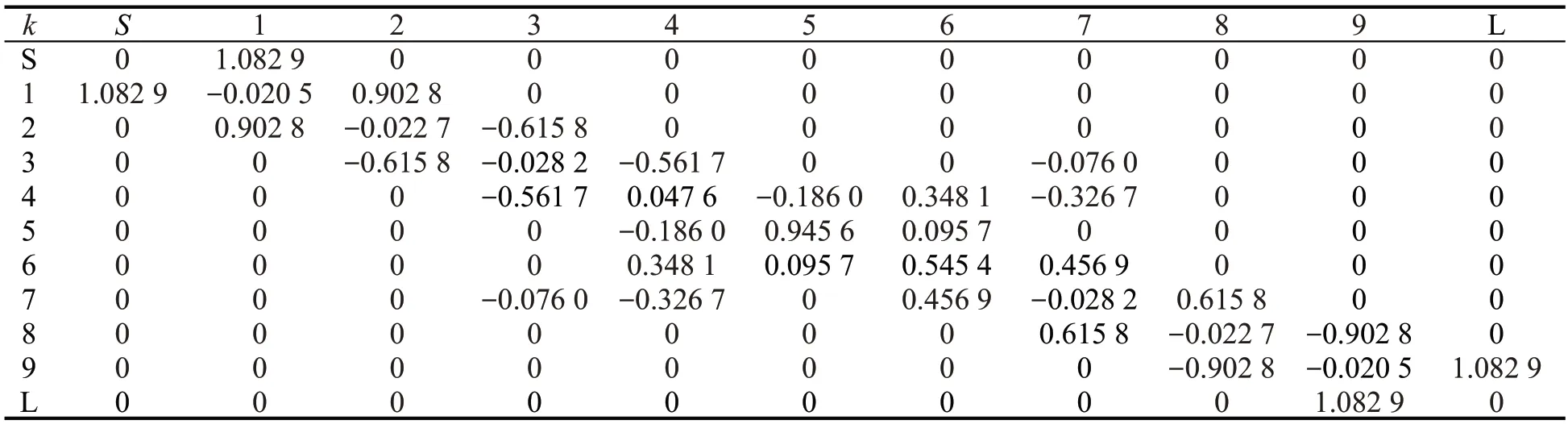
表6 理想的耦合矩阵

表7 最终提取的耦合矩阵

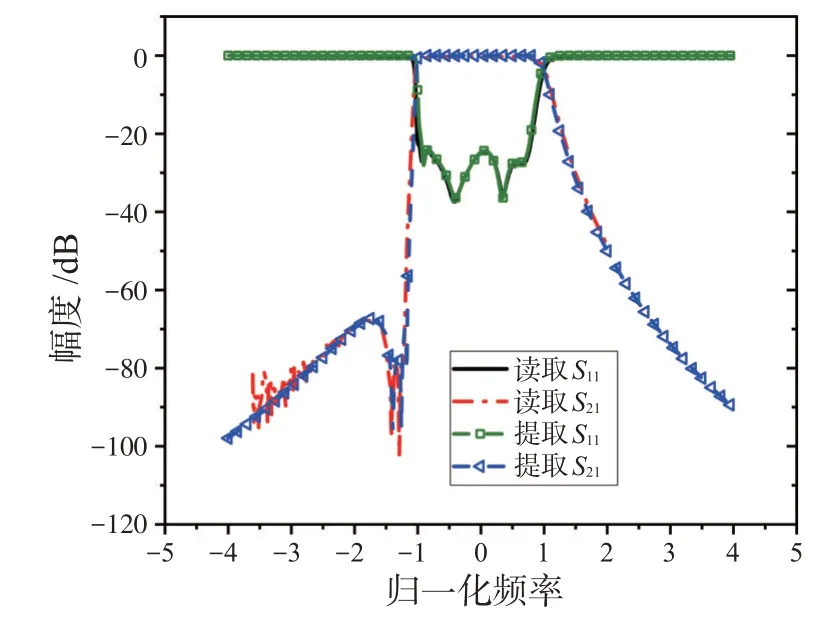
图8 最终参数提取S曲线

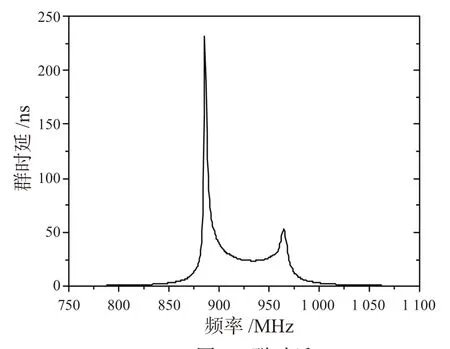
图9 群时延

由实验结果分析可知，本文所提方法在滤波器的群时延、S曲线提取、耦合矩阵等关键指标的获取方面表现良好，具有较强的有效性和适用性。

4 结束语

本文运用遗传算法来优化传输零点以及耦合矩阵，解决了传输零点未知的问题。通过读取S参数文件进行取样，作为遗传算法的初始种群，结合寻找最优传输零点位置以及耦合矩阵的目标函数，实现了九阶三零点的交叉耦合滤波器的耦合参数提取。结果显示，理论分析得到的S参数曲线和读取数据曲线吻合较好。相对于手动调优方法而言，该方法有助于滤波器的快速调试，以便实现交叉耦合结构腔体滤波器电性能达到理想指标，满足实际需求。