具有非局部竞争的Holling-Tanner捕食模型的稳定性分析

杨尤伟，伍代勇

（安庆师范大学 数理学院，安徽 安庆 246133）

针对捕食者-食饵种群相互作用的问题，学者们建立了各种捕食者-食饵的数学模型。例如，YAMADA[1]建立了具有齐次狄利克雷边界条件的扩散捕食模型，并通过讨论非负平衡点的稳定性来描述栖息在同一有界域内的食饵和捕食者种群密度的演化。DUBEY[2]建立了具有恐惧效应和反捕食行为的捕食模型，并揭示了食饵种群密度不仅受捕食者直接捕杀的影响，而且食饵对捕食者的恐惧也会使其降低繁殖率。此外，ZHANG[3]建立了食饵趋化模型，并研究了食饵趋化对系统动力学行为的影响。继LOTKA 和VOLTERRA 的开创性工作后，为了研究猞猁和兔子种群之间的相互作用，Holling-Tanner 捕食者-食饵模型被提出[4]。在Holling-Tanner模型基础上，学者们结合捕食者趋向性[5]和Allee效应[6]等进行了深入研究。

在经典的种群动力学模型中，许多学者倾向于在局部意义上对种群竞争进行建模，即位于x处的种群竞争强度仅依赖于x处的种群密度。然而，在复杂生态环境中，大家逐渐认识到位置x处的个体生长速度会受到其他空间个体的影响。FURTER等[7]提出了种群个体可以通过视觉或化学手段进行交流。在数学上，局部食饵竞争-u2(x,t)用非局部食饵竞争来代替，其中G(x,y)表示核函数[8]，Ω 表示物种栖息地。近几年来，也有众多学者开展了关于非局部食饵竞争的研究。CHEN等[9]考虑了具有Neumann边界条件的非局部相互作用捕食者-食饵系统，并认为Hopf分岔更可能发生在非局部食饵竞争中，而正常稳态的稳定周期轨道分岔可能是空间非齐次。此外，非局部效应可导致多种空间模式。例如，空间非齐次周期解可能由非局部效应所引起[10]。WU等[11]研究了非局部食饵竞争对具有Holling II型功能反应的扩散Rosenzweig-MacArthur模型动力学行为的影响，且表明了非局部食饵竞争可以产生Turing斑图，而原始模型是不可能发生的。SHI等[12]研究了广义的种群系统Turing分岔和Hopf分岔的存在性，并证明了非局部食饵竞争可以诱导空间非齐次的周期模式。

由于河流、水深、经度、纬度等都可以被抽象为一维空间，同时为便于数学分析，本文在文献[4]基础上，提出了在一维空间下具有非局部食饵竞争的Holling-Tanner捕食模型。

其中，所有参数为正常数；u和ν分别表示t时刻x处的食饵和捕食者的种群密度；d1和d2分别表示食饵和捕食者的扩散系数；α是捕食者对食饵的攻击率；b是半饱和常数；β是捕食者的内禀增长率。

1 模型的平衡点和稳定性

注1当α ≤4b时，非局部食饵竞争模型（1）不会发生由扩散导致的空间齐次Hopf分岔。

接下来，讨论当n∈N时，Tr0(u*,ν*)、Trn(u*,ν*)和Dn(u*,ν*)的符号。

引理1如 果β＞β*，那么Tr0(u*,ν*)＜0；如果β=β*，那么Tr0(u*,ν*)=0；如果β＜β*，那么Tr0(u*,ν*)＞0。

2 局部模型与非局部模型比较

接下来，主要分析非局部项对模型稳定性的影响。类似本文第1节计算可得，局部食饵竞争模型对应雅可比矩阵的迹和行列式为

通过与非局部食饵竞争模型对应雅可比矩阵的迹和行列式比较，得到

注3通过以上分析，有如果局部食饵竞争模型和非局部食饵竞争模型的稳定区域都存在，那么非局部食饵竞争模型在共存平衡点E*(u*,ν*)处对应的稳定区域则包含于局部食饵竞争模型对应的稳定区域。因此，非局部项使得共存平衡点E*(u*,ν*)失稳。

3 数值模拟

本节主要通过数值模拟来验证理论结果可行性。选取初值u0(x)=0.289+0.001cos和ν0(x)=0.289+0.001cos。固定参数α=1.200、b=0.200、d1=0.500、d2=0.100和l=1.000。计算得到，非局部食饵竞争模型（1）的共存平衡点E*(0.289,0.289)、l2-＜0、β*=0.130 和1.050，同时得到β**=1.050。选取β=1.200 ＞1.050，由定理1 可知，非局部食饵竞争模型（1）的共存平衡点E*(0.289,0.289)呈现局部渐近稳定，如图1所示。

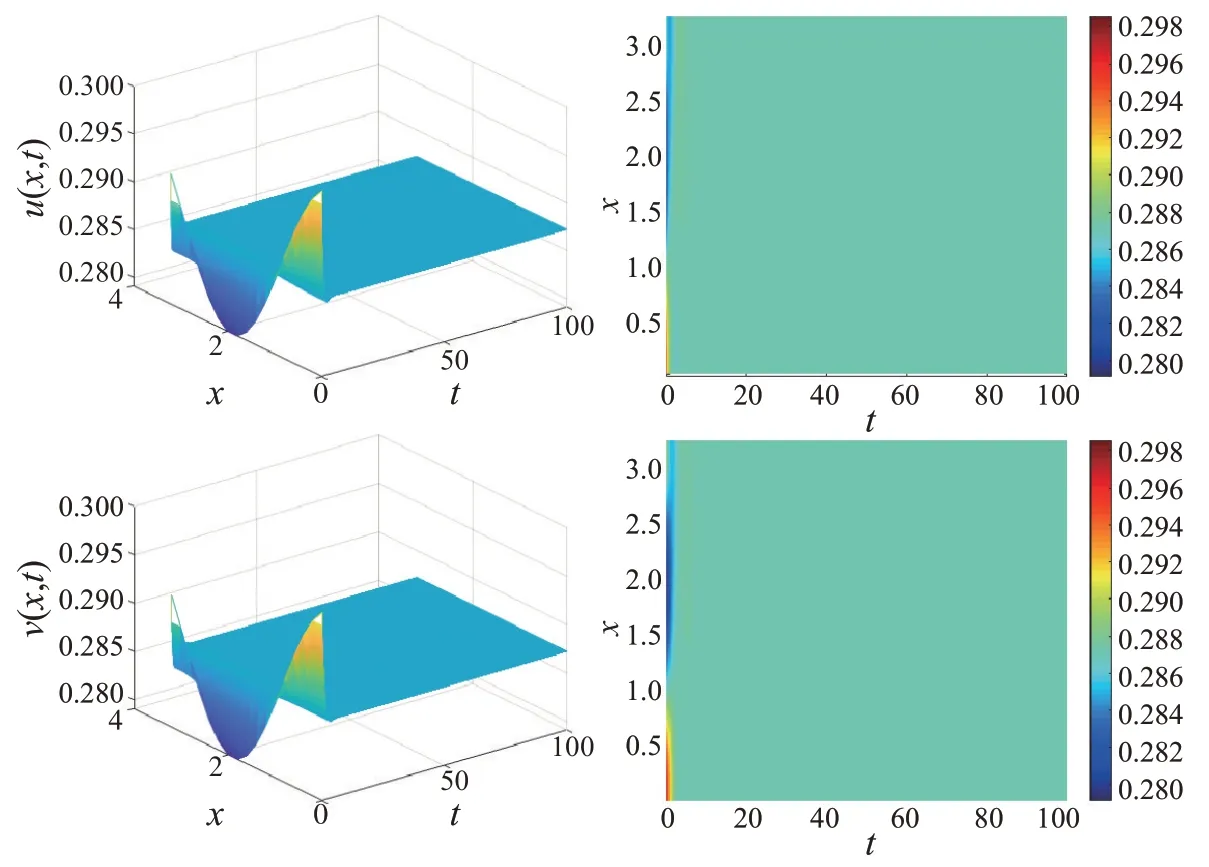
图1 非局部模型β=1.200对应的捕食者-食饵种群时空分布

固定参数α=1.200、b=0.200、d1=0.500、d2=0.100 和l=1.000，计算得到非局部食饵竞争模型（1）的共存平衡点E*(0.289,0.289)、β*=0.130 和=0.084。选取β=0.130，在共存平衡点E*(0.289,0.289)附近，非局部食饵竞争模型（1）经历空间齐次Hopf 分岔，如图2所示。比较图1和图2发现，随着捕食者内禀增长率的减小，非局部食饵竞争模型（1）由稳定转化为周期性振荡。

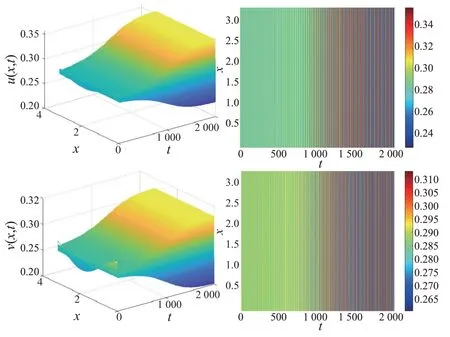
图2 非局部模型β=0.130对应的捕食者-食饵种群时空分布

本文在相同参数下比较了局部食饵竞争模型与非局部食饵竞争模型的差异性。固定α=1.200、b=0.200、d1=0.200、d2=0.050、l=2.000 和β=0.120。图3 表明局部食饵竞争模型对应的食饵和捕食者在空间上呈现均匀分布；而图4 表明非局部食饵竞争模型对应的食饵和捕食者在空间上是非均匀分布的。比较图3 和图4 可知，非局部食饵竞争导致了空间非齐次周期解的出现。

图3 局部模型对应的捕食者-食饵种群时空分布

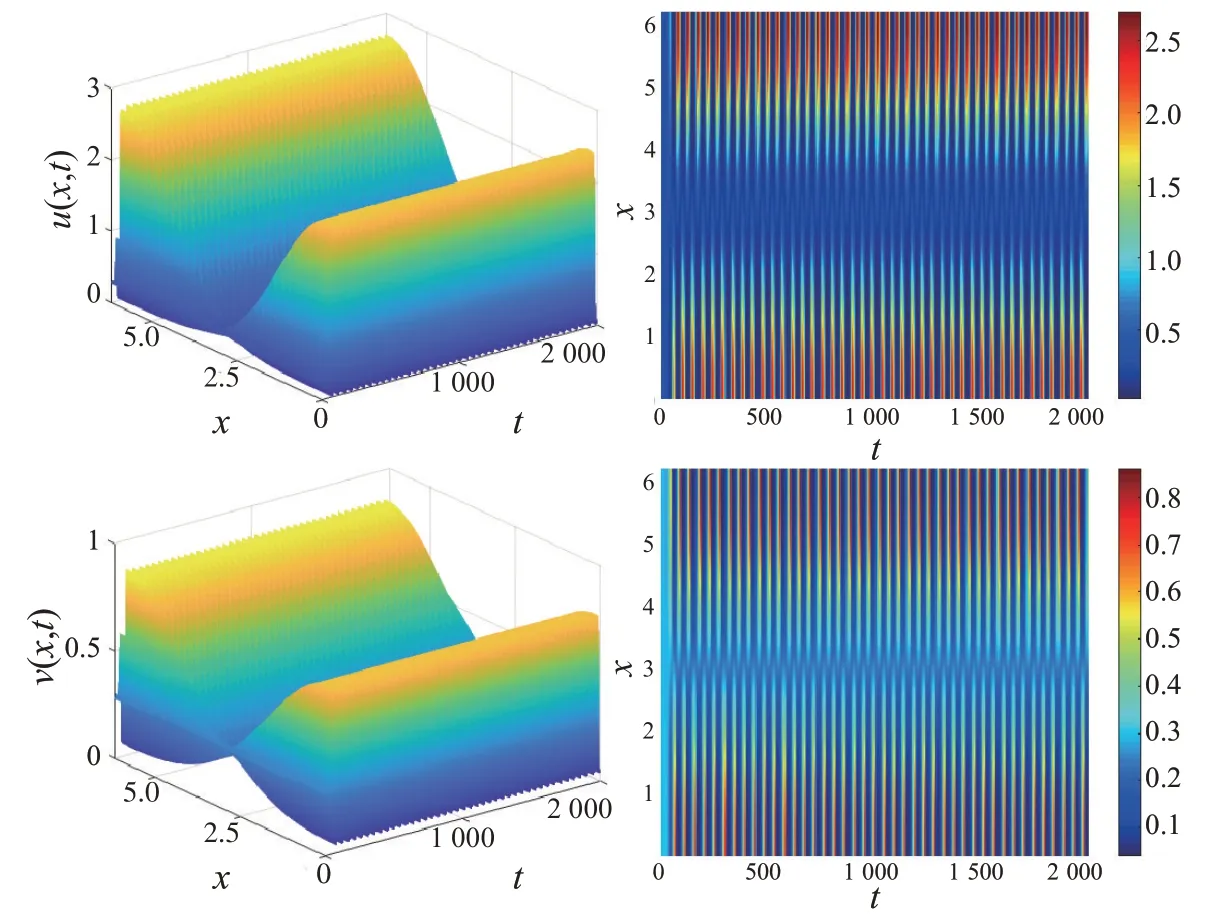
图4 非局部模型对应的捕食者-食饵种群时空分布

4 结束语

本文研究了具有非局部食饵竞争的捕食者-食饵模型，从生态学角度来讲，该模型描述了物种之间的竞争不仅依赖于某处位置的种群密度，而且还依赖于该位置附近的种群密度。在理论分析部分，本文给出了非局部食饵竞争模型共存平衡点稳定的充分条件。结合注3，我们发现非局部项可以使共存平衡点失稳。在数值模拟部分，比较图3与图4有，在相同参数下，非局部项使得物种在空间上的分布由均匀变为非均匀，可见非局部项对于物种的空间分布及稳定性都具有重要的影响，可使捕食者-食饵模型的时空动力学行为更加丰富。非局部食饵竞争模型的探讨为物种进化研究提供了新思路。