冷备系统剩余寿命近似计算方法

赵 骞, 谭 尧, 吴 波, 蒋 平,*, 郭 波

(1. 国防科技大学系统工程学院, 湖南 长沙 410005; 2. 国防科技大学信息通信学院, 陕西 西安 710106)

0 引 言

冗余是提高系统可靠性的重要技术,在工业和军事装备上被广泛应用[1-3],其可被进一步划分为热备、温备与冷备3种。热备指的是工作部件与备份部件处于相同的工作状态,冷备则认为备份部件在贮备期间不工作,失效率为零,而温备的部件失效率介于热备和冷备之间。n中取k冷备系统共由n个部件组成,至少需要k个部件正常工作才可以保证系统的正常运行。当工作位置部件发生故障,备份部件依次替换失效的工作部件继续工作,直至系统中能够正常工作的部件总数小于k时,冷备系统失效。

从装备质量特性与管理的角度,常常会关心当前正常工作的装备产品还能继续运行的时间,这就是产品的剩余寿命。准确的剩余寿命预测对于工业系统、装备系统任务完成、维修以及更换而言均意义重大，因而对复杂装备系统的剩余寿命预测具有极大的经济价值和战略意义。然而，因冷备系统结构复杂,对其剩余寿命估计的研究却相对较少。

许双伟等[4]通过分析部件状态之间的关系,并基于最小割集理论提出了一种计算可靠度和平均故障间隔时间的仿真算法。同时,基于不确定性理论,推导了3种不可修冷备系统的可靠度和平均失效时间(mean time to failure, MTTF)的解析表达式[5]。利用极大似然原理、Bayes估计和经验Bayes估计,部件服从Gamma分布的冷备系统失效率、可靠度以及平均寿命的估计方法可参见文献[6-7]。广义近似置信限以及E-Bayes方法在文献[8]中进行了研究。但是以上研究只针对n中取1冷备的特殊情况,并且缺少对剩余寿命估计的讨论。更进一步,Eryilmaz[9]通过计算得到了一个冷备部件的表决系统平均剩余寿命,但是当部件寿命分布复杂时,该方法同样面临局限性。应用Farlie-Gumbel-Morgenstern Copula函数完成对可靠度和MTTF的估计可参见文献[10-11]。事实上,这些研究也仅考虑了部件服从指数分布的情况。

虽然对于冷备系统剩余寿命的研究较少,但是对其可靠度的估计方法的研究相对较为成熟。周仲夏等[12]通过推导得到了n中取1的冷备系统可靠度的闭合表达式,类似研究也可参见文献[13]。通过运用马尔可夫过程,2n+1中取n的特殊冷备系统在文献[14]中进行了研究,类似研究还可参见文献[15-17]。这些方法的优势是可以获得闭合表达式,但是以上结论必须基于部件均服从相同指数分布这一假设。

由于计算较为复杂,数值计算和Bayes理论等方法得到了进一步应用。Levitin等[18]提出了基于通用生成函数获取n中取k的冷备系统可靠度函数的方法。这也为本文进行剩余寿命估计奠定了重要基础。事实上,在部件寿命已知的情况下,冷备系统可靠度可以通过卷积进行计算,但是往往由于计算复杂,无法或者难以通过推导得到冷备系统可靠度的解析表达式。Amari等[19]通过梯形法实现了卷积的近似计算。一些学者尝试运用Bayes理论进行可靠度估计[20-22]。Jia等[23]基于马尔可夫链-蒙特卡罗方法获得可靠度Bayes估计。

综上所述,对于n中取k的冷备系统剩余寿命的估计比较困难,特别是当部件服从复杂分布时,相关研究更为缺乏。基于此,本文首先研究了剩余寿命估计与可靠度函数之间的关系,证明了剩余寿命计算的核心是获得系统可靠度,然后通过研究给出解析方法、数值方法以及仿真方法,获得了冷备系统任意时刻的可靠度,在此基础上基于组合辛普森公式,提出一种基于任意时刻可靠度近似计算剩余寿命的方法,高效、准确地获得了冷备系统剩余寿命的点估计与区间估计。

1 基于可靠度函数的剩余寿命预测方法

1.1 剩余寿命的概率密度函数

假设T为产品寿命,F(t)、f(t)和R(t) 分别表示产品失效时间的累积分布函数(cumulative distribution function, CDF)、概率密度函数以及可靠度函数。则该产品在工作到当前时刻τ时,剩余寿命分布函数FL(t)[9]为

(1)

式(1)对t求导,可得剩余寿命概率密度函数为

(2)

1.2 可靠度函数与剩余寿命

τ时刻,剩余寿命点估计Eτ(TL)为

(3)

将式(2)代入(3)可得

其中,

将其代入式(3)可得剩余寿命点估计为

(4)

假设剩余寿命100(1-α)%置信水平下的双侧区间为[μL,μH],则μL与μH需满足:

(5)

也可记为

(6)

从式(4)和式(6)均不难看出,要得到冷备系统剩余寿命的点估计与区间估计,核心是获得该系统可靠度。本文将在第2节,针对冷备系统组成部件寿命分布的不同情况,依次介绍解析方法、数值方法以及仿真方法3种可靠度计算方法。

2 可靠度的计算

2.1 解析方法计算可靠度

对于部件服从相同指数分布的情况,根据已有文献研究,可以通过解析推导得到冷备系统可靠度的闭合表达式。

例如n中取1的冷备系统,假设n个部件的寿命为X1,X2,…,Xn,相互独立且均服从失效率为λ0的指数分布,则冷备系统的可靠度可以表示为

R(t)=1-P(X1+X2+…+Xn≤t)

由拉普拉斯变换及逆变换[12]可得

(7)

更一般地,对于n中取k冷备系统,部件仍服从失效率为λ0的指数分布,可靠度[24]为

(8)

文献[25]推导了该种情况下τ时刻冷备系统剩余寿命的闭合表达式为

(9)

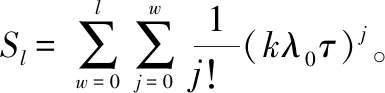
(10)

式(9)与式(10)的推导结果将在算例中进行运用,作为该种情况下的理论值与本文第2.2节所提方法进行对比。

2.2 数值方法计算可靠度

由于指数分布相对简单,可以推导得到对应的冷备系统剩余寿命闭合表达式,对于更为复杂的情况,数值方法提供了新的解决思路。设k个工作部件中第i个(1≤i≤k)工作部件和对应该位置的备份部件寿命分布CDF分别为Fi(t)和Hi(t),令Gi, j(t)表示第i个部件所在的位置至少有j个部件已经失效。不难得到

Gi, j(t)=Gi, j-1(t)*Hi(t)

(11)

式中：Gi,1(t)=Fi(t)。并且，

(12)

关于式(11)中的卷积,可以将积分区间划分为m个子区间,采用梯形法则进行数值计算,计算精度随着m的增大而提高[19]。令Pi, j(t)表示t时刻在i个部件所在位置上正好发生j个失效的概率,因而

Pi, j(t)=Gi, j(t)-Gi, j+1(t)

(13)

且Pi,0(t)=1-Gi,1(t)。

令Pj(t)表示t时刻系统中共有j个部件失效,容易看出Pj(t)可由所有位置的Pi, j(t)计算得到。则当系统失效个数小于n-k+1时,系统正常工作,所以冷备系统的可靠度为

(14)

值得一提的是,上述数值计算方法要求同一位置上工作的部件需要服从相同分布,因而也面临一定局限性。

2.3 仿真方法计算可靠度

对于更为复杂的情况,可采用仿真抽样从而得到任意时刻的可靠度,抽样算法如算法1所示。

算法1 冷备系统可靠度估计抽样方法已知:给定系统n个部件寿命分布概率密度函数fi(t)(1≤i≤n) 和抽样次数S,任意工作时刻τ,令count=0。步骤1 由fi(t)(1≤i≤n)分别抽样得到部件寿命样本L1,L2,…,Ln,令工作位置的累计寿命CLi=Li(1≤i≤k),p=1;步骤2 寻找到所有CLi (1≤i≤k)中的最小值,在该CLi上增加Lk+p,并令p=p+1;步骤3 重复步骤2,(n-k)次后,可以得到最终k个CLi值,则系统寿命Ls=miniCLi(1≤i≤k);步骤4 If Ls≥τ, then count+1;步骤5 重复步骤1～步骤4 S次,τ时刻的可靠度近似值为R(τ)=countS。

需要指出的是,仿真方法适用于分布更为复杂的情况,在实际应用中,仅需要将算法进行对应调整即可,本文在算例中也将进行详细分析。

3 剩余寿命的近似计算

3.1 组合辛普森公式

第2节讨论了不同情况下获得冷备系统任意时刻可靠度的方法。由式(4)可知,要对分子中的积分进行计算，相对复杂,很多情况下难以推导得到闭合表达式,即使获得了冷备系统可靠度的解析表达,由于其形式复杂,积分计算工作量也很大,因此本节基于组合辛普森公式引入近似计算方法。近似计算方法简单高效,适用范围广,表现出了更大的优势。利用可靠度函数与剩余寿命的关系,在通过解析、数值、仿真方法获得任意时刻系统可靠度的基础上,可以通过求解得到剩余寿命的点估计与区间估计。

对于式(4),本文采用组合辛普森公式进行计算。

如果f(x)∈C4[a,b],则存在ξ∈[a,b],使得[a,b]上w个子区间的组合辛普森公式和截断误差项[26-27]满足:

(15)

式中：h=(b-a)/w;f(4)(ξ)为f(x)在ξ的四阶导数。

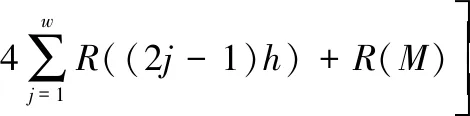
(16)

式中：M为足够大的正数;w为划分的区间个数,且h=(M-τ)/ω。显然,M的取值对结果会产生影响,相关分析见第4.1.1节。

3.2 误差分析

上述方法计算剩余寿命的误差主要存在于采用梯形法则近似计算卷积产生的误差,采用辛普森公式求解积分产生的截断误差以及将无限区间的积分转化为有限区间积分所产生的截断误差。一般地,区间划分个数m,ω越大,以及所选有限区间[τ,M]中的区间上限M越大,计算精度越高,误差也越小。剩余寿命方差推导如下:

(17)

其中,

(18)

所以,随机变量TL的方差为

(19)

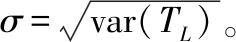
4 算例分析

4.1 部件服从指数分布的冷备系统

以5中取2的冷备系统为研究对象,假设部件完全相同并且相互独立,均服从失效率λ0=0.01h-1的指数分布。

4.1.1 区间的确定

由式(10)和式(19),可得寿命分布的期望为E(TL)=200 h,方差为var(TL)=1×104h2。表1展示了在积分区间上限M的不同设定下,寿命的点估计计算结果。

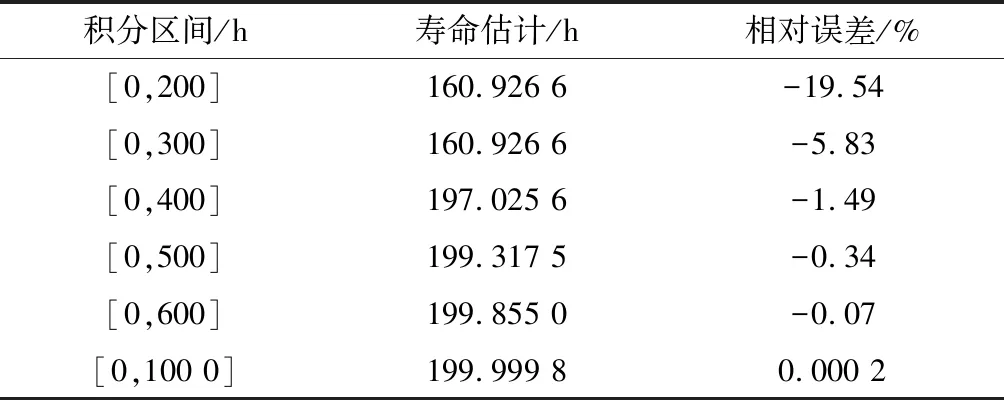
表1 不同积分区间下的相对误差

由表1可知,一般情况下,取值区间上限M越大,计算所得到的寿命以及剩余寿命点估计值越准确。分析表1可知,积分区间上限为E(TL)+4σ时,误差已经明显降到1%以下,因而可确定剩余寿命积分区间范围为[τ,E(TL)+4σ]时,能基本满足误差要求,当然在计算时间允许范围内,M的取值越大,估计结果越精确。

4.1.2m的确定

在确定积分区间上限M的基础上,需要研究使用梯形法则时,区间划分个数m的确定方法和原则。为了更清晰地进行比较,首先利用式(1)和式(8)获得当前工作时刻为τ=20 h时剩余寿命的理论CDF,然后通过本文提出的数值方法,分别画出m分别取10,100,500时,剩余寿命的CDF图像，如图1所示。

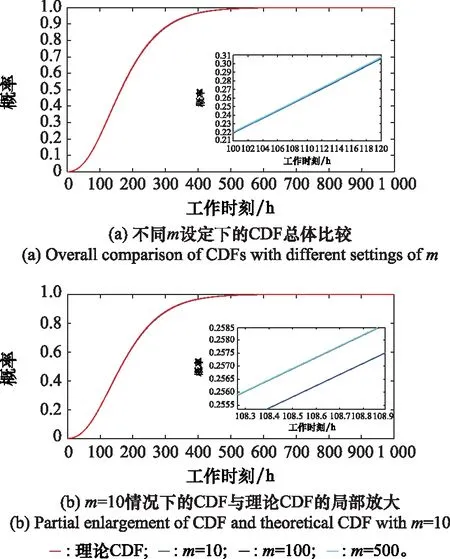
图1 不同m设定下的CDF比较Fig.1 Comparison of CDFs with different m

需要说明的是,为了便于对比,图1(a)和图1(b)均插入了局部放大图,且放大比例依次增大。通过分析图1(a)可以看到,在3种m设定下,误差均比较小。但在继续局部放大得到图1(b)后可以发现,m=10所对应的CDF图像与理论CDF图像存在较明显的偏差,但是m=100和m=500所得到的两条曲线仍然没有明显区别。因而一般情况下,m值越大，结果越准确,考虑计算成本,令m=100更好。

4.1.3w的确定

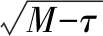
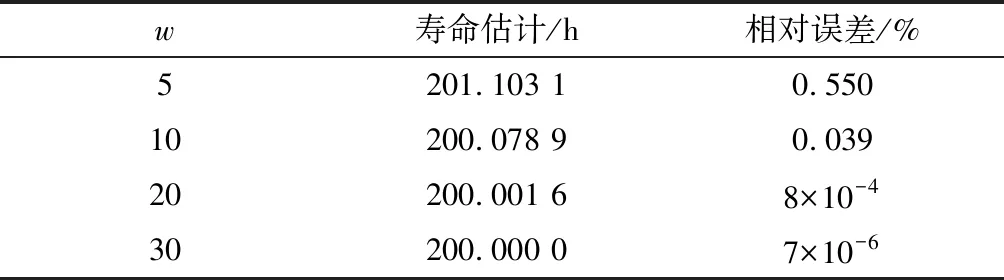
表2 不同w下的相对误差表

4.1.4 剩余寿命验证

第4.1.1至第4.1.3节先后研究了影响近似计算方法精度的因素,为了进一步验证在部件服从相同指数分布情况下,n中取k的冷备系统剩余寿命估计方法的准确性,改变参数值,利用式(7)求得冷备系统可靠度函数,进而利用式(16)计算出剩余寿命近似值,并将该近似计算结果与由文献[25]推导的剩余寿命点估计闭合表达式(式(9))进行比较，比较结果如表3所示。

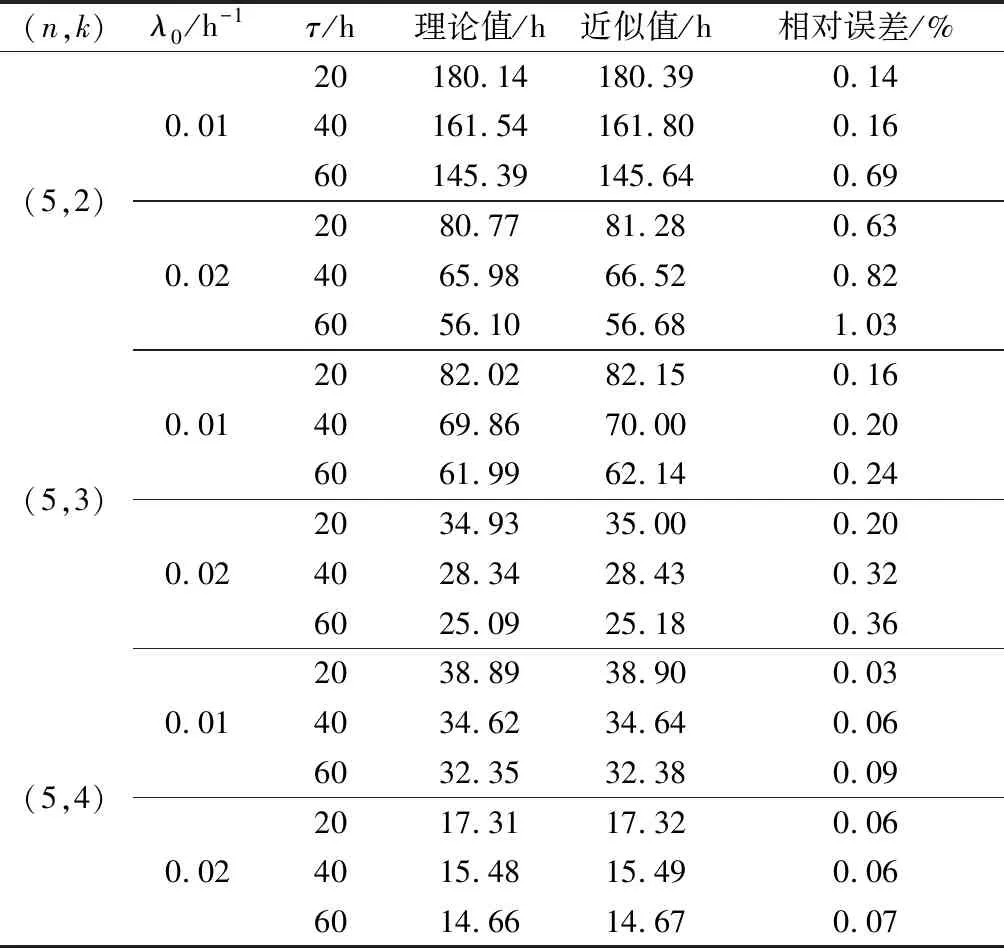
表3 不同参数下的剩余寿命估计结果

由表3可以看出,在部件寿命服从相同指数分布的情况下,本文提出的数值方法求解冷备系统剩余寿命的方法计算结果准确,误差均在可接受范围内。

4.2 部件服从相同威布尔分布的冷备系统

为进一步验证本文所提方法,假设部件寿命服从相同的威布尔分布,威布尔分布CDF如下:

(20)

式中:η,β为威布尔分布参数[28-30]。

针对部件服从威布尔分布的情况,运用第2.2节数值方法获得任意时刻该冷备系统的可靠度,然后运用辛普森公式得到剩余寿命的近似估计。为了进行结果验证,与仿真方法进行对比,设定抽样次数S=10 000，验证结果如表4所示。

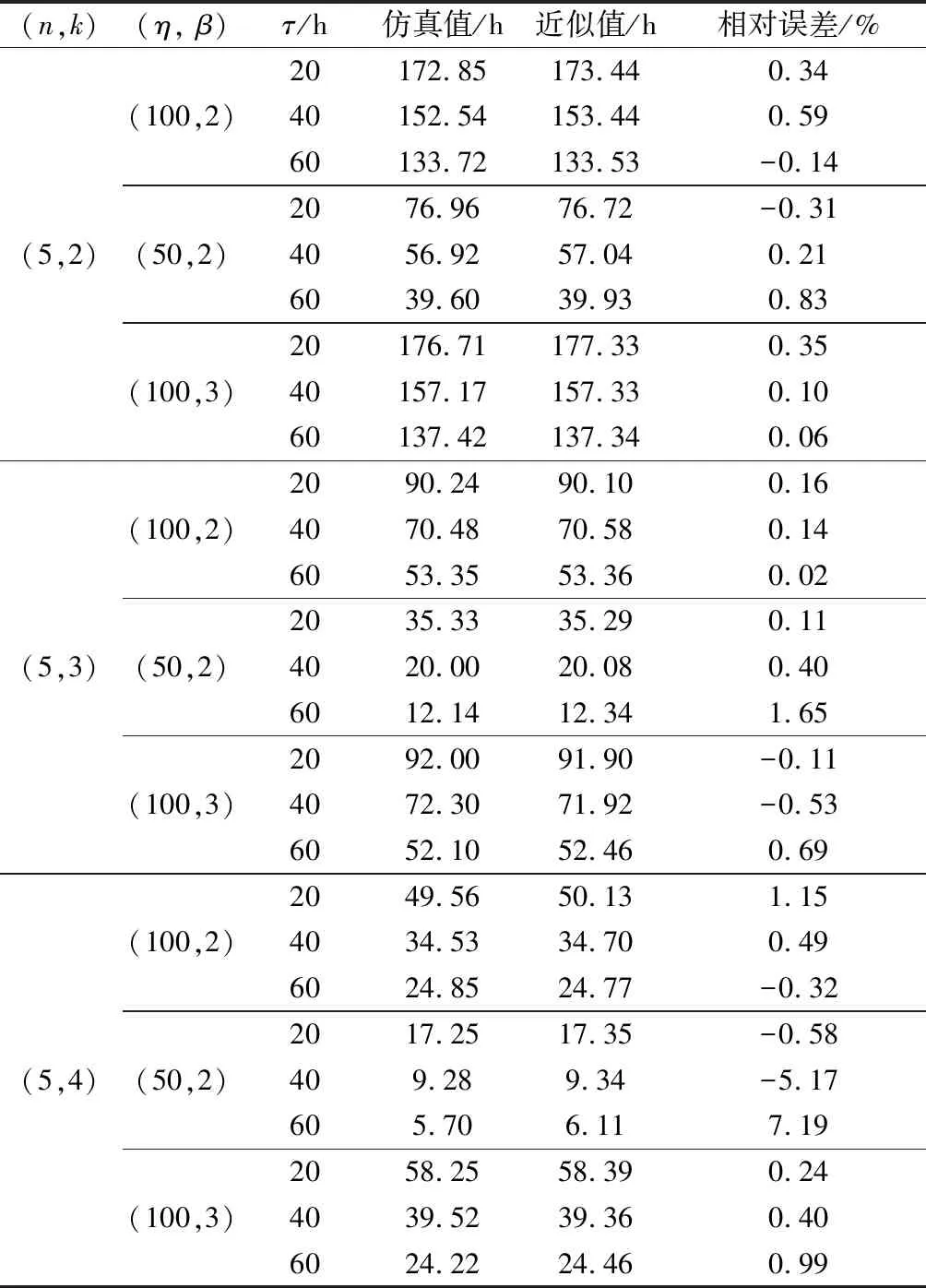
表4 部件服从威布尔分布时不同参数下的剩余寿命估计结果

由于CDF图像能够反应更详细的比较信息,因而根据表4第1组实验参数设置(n=5,k=2,η=100,β=2,τ=20),利用仿真方法和数值方法绘制的剩余寿命CDF图像如图2所示。

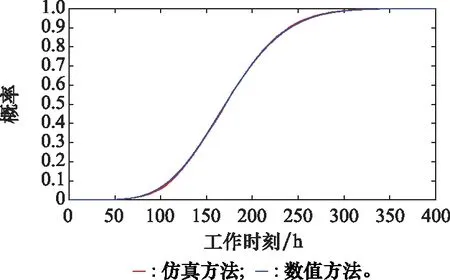
图2 部件服从威布尔分布情况下仿真方法和数值方法 得到的CDF比较Fig.2 Comparison of CDFs between simulation method and numerical method with components following Weibull distribution

仍以表4第1组实验为例,在得到任意时刻可靠度的基础上,由式(9)可以分别得到两种方法的剩余寿命区间估计,假设置信水平为90%,比较结果如表5所示。

表5 实验1剩余寿命点估计与区间估计

通过表4、表5和图2可以发现,本文提出的数值方法无论从剩余寿命点估计、区间估计或是CDF图像考量,结果都比较准确,误差在可接受范围内。

4.3 更为复杂情况下的冷备系统

对于更为复杂的情况,第2.1节与第2.2节提出的解析方法与数值方法均无法获得冷备系统可靠度,所以采用第2.3节所提出的仿真抽样方法。以8中取4的冷备系统为例,假设4个位置部件均服从威布尔分布,分布参数(η,β)分别设定为(110,2.25), (120,2.50), (130,2.75), (140,3.00)。其工作到τ=20 h 时系统未失效,通过仿真抽样,近似计算得到其剩余寿命的估计值为150.95 h,区间估计为(90.80,218.11)h。其剩余的CDF图像如图3所示。

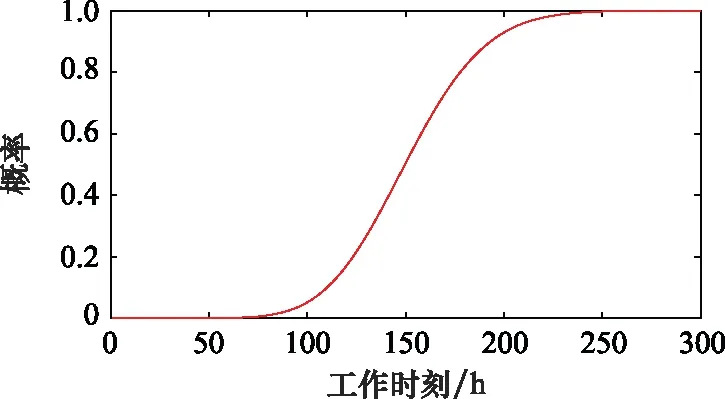
图3 不同位置部件服从不同威布尔分布时冷备系统 剩余寿命CDF图像Fig.3 CDF image of residual life of cold standby system for components at different positions following different Weibull distributions

仍以上述情况为例,假设初始时,工作部件与冷备部件分别服从不同威布尔分布,分布参数(η,β)分别为 (100,2), (140,3), 其工作到τ=20 h 时系统未失效,则通过计算得到剩余寿命估计值为140.55 h,区间估计为 (71.11,219.08)h。剩余的CDF图像如图4所示。

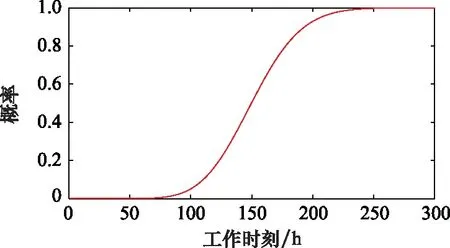
图4 部件服从不同威布尔分布时冷备系统剩余寿命CDF图像Fig.4 CDF image of residual life of cold standby system for components following different Weibull distributions

通过上述实验可以看出,对于更为复杂的情况,解析方法、数值方法面临局限性,但是仿真方法在牺牲了可接受的时间成本的基础上,弥补了前者的不足。

5 实例计算

冷备作为重要冗余技术,在航空航天产品中得到了非常广泛的应用。例如，文献[31]研究了一种工程中存在的典型冷备系统,即指数-威布尔混合型冷备系统。该系统工作部件为电子设备,服从指数分布,而冷贮备部件为机电设备,服从威布尔分布。由于推导复杂,文献[31]也只是研究了一备一系统,即2中取1的冷备系统。本文针对文献[31]所提到的开关完全可靠和开关寿命为指数分布两种不同情况进行了对比验证。

5.1 开关完全可靠

当转换开关完全可靠时,在模拟分析中,文献[31]假设工作部件服从失效率为λ=0.15的指数分布,冷贮备部件服从η=2,β=1.5的威布尔分布。

运用本文第2.2节所提出的基于梯形法则的计算方法,可以快速得到任务时刻τ=2时,该冷备系统的可靠度为0.916 7。这与文献[31]中的计算结果一致,说明本文所提方法准确合理。

文献[32]基于Fiducial方法给出了冷备系统的置信下限,该方法同时也可以得到冷备系统可靠度的点估计。运用该方法计算得到上述系统可靠度点估计为0.915 1,与本文方法及文献[31]中方法的计算结果一致,再一次证明了本文方法的准确性。同时,利用文献[32]中方法计算得到可靠度95%置信区间的下限为0.904 7。多次利用本文第2.3节中的仿真方法得到该系统的多个可靠度点估计样本,同样也可以计算得到可靠度置信下限,为0.903 0,与文献[32]的计算结果一致。说明本文方法也可以很好地解决置信下限点估计问题。

进一步,在获得任意时刻该冷备系统可靠度后,利用辛普森公式,计算得到该系统在工作时刻τ=2时，剩余寿命为7.105 5,剩余寿命90%置信区间估计为(0.518 5,20.825 7)。

根据剩余寿命计算结果,可以合理安排该冷备系统的更换、维修等策略,与文献[31]仅仅给出冷备系统可靠度相比,文献[32]给出的可靠度置信下限更具意义。

5.2 开关寿命为指数分布

文献[31]还研究了转换开关不可靠的情形,并且假设转换开关失效时间服从指数分布,失效率为λb=0.15。同时，工作部件服从失效率λ为 0.15的指数分布,冷贮备部件服从η=3,β=1.5的威布尔分布。此时,需要采用第2.3节的仿真方法获取冷备系统可靠度。

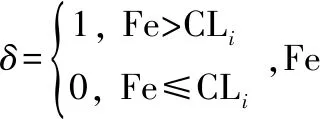
根据仿真抽样样本,该冷备系统寿命样本及其拟合概率密度曲线如图5所示。

图5 开关寿命为指数分布时冷备系统寿命概率密度曲线Fig.5 Probability density function curve of cold standby system life with exponentially distributed switch life

通过计算可以得到,任务时刻τ=2时的可靠度为0.918 7,这与文献[31]中的计算结果(0.918 8)基本一致。同时,根据本文方法可以得到任意时刻可靠度,所以运用辛普森公式便可以计算得到开关寿命为指数分布时该冷备系统的剩余寿命为6.711 7,90%剩余寿命置信区间为(0.573 9,18.960 2)。

由于结构复杂,文献[31]的研究具有如下局限性:① 仅考虑了2中取1冷备系统;② 工作部件和备份部件分布形式固定,分别服从指数分布与威布尔分布;③ 仅研究了可靠度估计,并未给出剩余寿命估计。本文所提方法解决了上述难题,并且通过对比实验再次说明,本文所提出的通过仿真获取任意时刻可靠度、进而估计剩余寿命的方法能够解决部件分布复杂、开关不可靠等更加多样、复杂的实际情形,具有很好的适用性。

6 结 论

冷备系统日益受到关注,但是因其结构复杂,针对复杂冷备系统剩余寿命的研究较少。基于此,本文提出了n中取k冷备系统剩余寿命点估计与区间估计的近似计算方法。通过推导发现,对于冷备系统剩余寿命估计的核心是获得其可靠度函数。本文提供了不同情况下,获得冷备系统可靠度的解析方法、数值方法以及仿真方法。在此基础上,基于组合辛普森公式,利用上述方法得到任意时刻可靠度,便可完成冷备系统剩余寿命的点估计和区间估计。

算例分析部分讨论了与估计误差密切相关的积分上限M、卷积区间划分个数m、积分区间划分个数w的一般确定原则,并且通过部件服从相同指数分布、威布尔分布两种情况对本文提出的近似计算方法进行了检验。当部件服从更为复杂的分布时,本文所提方法仍可以解决剩余寿命点估计和区间估计问题,适用范围广。

同时,本文在最后的实例计算部分,采用已有论文数据进行计算,并与原论文计算结果进行了对比,说明了本文计算方法准确可靠,同时也解决了原论文研究中存在的局限,具有较大的工程应用价值。