星敏感器姿态测量算法研究

段 辉, 周召发,*, 张志利, 徐志浩, 郝诗文, 曾 进

(1. 火箭军工程大学导弹工程学院, 陕西 西安 710025;2. 火箭军工程大学兵器发射理论和技术国家重点学科实验室, 陕西 西安 710025;3. 飞行自动控制研究所惯性技术航空科技重点实验室, 陕西 西安 710065)

0 引 言

星敏感器视场内可同时观测多颗恒星,每颗恒星在天球系与星敏系中具有不同的矢量坐标。因此,星敏感器可同时获得多个矢量对信息。利用这些矢量对信息,即可基于多矢量定姿算法解算出星敏系到天球系的坐标系变换矩阵C1,进而确定星敏感器的坐标轴在天球系中的指向。星敏感器在载体上固定安装,载体系到星敏系的坐标系转换矩阵C2(即安装矩阵)事先已经标定好,载体系到天球系的坐标系转换矩阵则为C1C2。几乎所有的确定性姿态算法都是基于Grace Wahba在1965年提出的一个问题,称为Wahba问题。Wahba问题通过最小化损失函数找到最优姿态矩阵[1],求解Wahba问题的目的是试图找到使损失函数最小的姿态矩阵C。

Farrell等[2]从矩阵伪逆的角度出发求解Wahba问题,仿真实验结果表明,估计出的三轴姿态稳定性差,具有较弱的鲁棒性,且计算量大,处理速度慢。Horn等[3]通过理论推导指出,求解矩阵特征值及其对应的特征向量时,传统的方法会同时将所有的特征值及其对应的特征向量都求解出来,而在对三轴姿态作最优估计时,往往只需要其中的最大特征值及其对应的特征向量,其余值都是冗余的,因此会提高算法复杂度,浪费计算资源。所以,为避免该问题,Horn等将瑞利商引入到最优姿态估计中。Markley等[4]并没有采用传统的求解思路,而是通过理论推导将最优姿态估计问题转化为已知数据构成的矩阵的奇异值分解(singular value decomposition, SVD)问题,对矩阵进行SVD可以充分保证算法的鲁棒性,但相对而言在算法执行效率上需要作出让步。在求解特征值及其对应特征向量时,Yang等[5]推导出了一种新的求解一元四次方程根的方法,进而求解出相应矩阵的最大特征值及其特征向量,该方法未存在近似步骤,属于纯解析解法,因此精度高且执行效率高,但前提是方程必须具有实根。Wu等[6]提出了线性估计算法,该方法不依赖于Davenport的q方法,而是另辟蹊径将最优姿态四元数的二次求解问题转化为一次求解问题,最终通过求解矩阵的特征值与特征向量得到姿态的最优估计。Shuster等[7]给出了一种新的姿态四元数估计(quaternion estimator, QUEST)算法,该方法首先基于哈密尔顿-凯勒定理构造封闭形式的特征多项式,并通过理论推导出最接近1的特征值所对应的特征向量就是要求的最优姿态四元数,最后,使用非解析的迭代方法求解。该方法中迭代次数无法给出一个确定值,所以迭代效果有时不太稳定。此外,郑振宇等[8]将无纬度支持定姿问题转换为对地轴矢量在参考坐标系下投影的解算问题,针对晃动基座下的地轴矢量解算问题,提出了一种基于旋转四元数的轴向矢量优化解算方法,并通过船载实验验证了该解算方法的优越性。Yan[9]为了增强姿态阵优化算法的实用性,给出了一种快速SVD优化算法,其浮点乘法计算量与四元数优化快速算法相近。

1 坐标系定义

天球坐标系与星敏感器坐标系的相对姿态如图1所示。

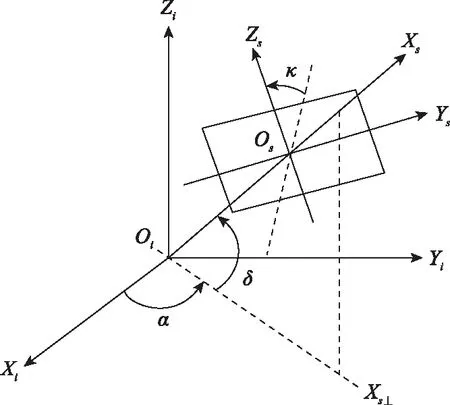
图1 天球系和星敏系相对关系图Fig.1 Relative diagram of celestial sphere system and star sensor system

天球坐标系Oixiyizi(第二赤道坐标系,简称i系):原点是春分点,基圈是天赤道,始圈是春分圈。天球坐标系的经度称赤经,纬度称赤纬。其赤经自春分点向东度量,属于左旋系统。赤纬自天赤道起沿天体所在的赤经圈向南北两个方向度量,为0°～90°。按北半球习惯,天赤道以北为正,天赤道以南为负[10-11]。

星敏感器坐标系Osxsyszs(简称s系):原点在星敏感器的透镜中心,Osxs轴沿光轴方向,Oszs轴沿透镜平面横轴向右,Osys轴沿透镜平面内垂直于Oszs的方向,并与Osxs、Oszs轴遵循右手法则。星敏感器坐标系与像平面坐标系的关系如图2所示。

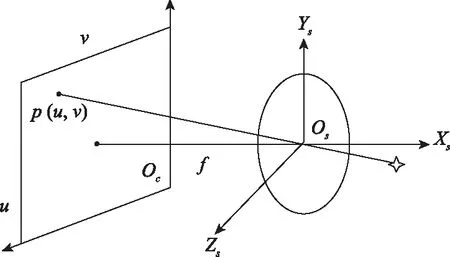
图2 星光矢量成像示意图Fig.2 Schematic diagram of star light vector imaging

天球坐标系与星敏感器坐标系的相对姿态可由星敏感器的姿态角给出,星敏感器的姿态角定义为偏航角α、俯仰角δ和滚动角κ。偏航角α为Osxs轴正方向所代表的矢量在天球坐标系下的赤经;俯仰角δ为Osxs轴正方向所代表的矢量在天球坐标系下的赤纬;天球坐标系绕Oizi轴旋转偏航角α、绕Oiyi轴旋转俯仰角δ后,Oixi轴与Osxs轴重合,此时天球坐标系只需再沿Oixi轴顺时针旋转κ度即可与星敏坐标系重合,这个角度κ定义为横滚角[12-15]。

(1)

需注意的是,实际运用中普遍是利用罗德里格斯旋转公式得到姿态矩阵与姿态四元数的转换关系,进而将姿态矩阵求解问题转化为姿态四元数求解问题以得到姿态四元数q,从而避免了引入奇异性问题并在一定程度上提高计算效率,具体的求解算法见下文。

2 星敏感器测量模型

星敏感器的姿态确定过程可简述为:进入星敏感器视场内的恒星星光经过电荷耦合器件(charge-coupled device, CCD)平面的光电转换形成数字星图,星图经去噪、星点提取后进行质心定位操作。至此,星光矢量的星敏系坐标已得到,再经过星图识别,则可得到CCD平面上星点的星表编号与赤经、赤纬等信息,进而得到星光矢量在天球坐标系中的三维坐标[16-19]。根据多个星光矢量的矢量信息对,就可以通过确定性姿态算法解算出天球坐标系到星敏坐标系的坐标变换矩阵。恒星星光矢量在CCD平面上的成像过程如图2所示,其理想的变换关系为

(2)

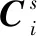
恒星星光矢量的像平面系坐标为p(u,v)[20]。

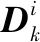
某一时刻,进入星敏感器视场内的恒星有n颗,经过一系列预处理步骤后,可得这n颗恒星的矢量信息对,其在星敏系和天球系中的坐标分别为

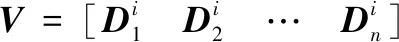
(3)

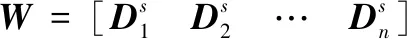
(4)

星敏感器的实际姿态测量模型为[25-31]

(5)

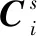
3 星敏感器姿态确定算法理论推导

3.1 LS算法

最小二乘(least square, LS)法主要用于参数估计,运用于天文定姿领域时,则可把姿态矩阵的9个非独立元素看作是9个参数,利用星光矢量的三维坐标信息对这9个参数进行估计。最小二乘估计的模型可以表示为

AX=B

(6)

式中:A为n×m的数据矩阵且n≥m;X为m×1的待估参数;B为n×1的参考向量,一般假设B不带测量噪声。式(6)两边左乘AT,并同时左乘(ATA)-1,即可得最小二乘解X=(ATA)-1ATB。

需要注意的是,数据矩阵A必须满足rank(A)=m,即A为列满秩矩阵,这样才能保证ATA为可逆矩阵,最小二乘解才存在。

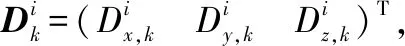
(7)

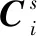
(8)

基于式(8),即可求解出最小二乘意义下的[C11C12C13]。同理,可求解出[C21C22C23]、[C31C32C33]。

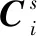
3.2 双矢量定姿算法

假设已识别出两颗视场内的恒星S1、S2,星敏感器坐标系和天球坐标系分别为Fs、Fi,S1、S2在星敏系中的坐标为Us、Vs,在天球系中的坐标为Ui、Vi(具体形式见式(3)),则可知下式成立:

(9)

式中:Us、Vs、Ui、Vi为3×1维坐标向量;Fs、Fi为3×3维坐标系矩阵。

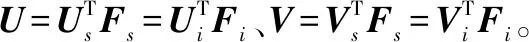
(10)

式中:C1为Fm和Fs之间的坐标系变换矩阵。

同理,还能得到Fm坐标系的另一种表达形式:

(11)

式中:C2为Fm和Fi之间的坐标系变换矩阵。

联立式(10)和式(11),可得

C1Fs=C2Fi⟹Fs=CFi

(12)

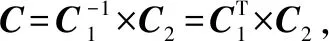
3.3 SVD算法

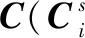
(13)

式中：ak为非负加权因子,由传感器的测量精度决定,一般有a1+a2+…an=1。

展开式(13)中的2范数平方项:

(14)

将式(14)代入式(13),得

(15)

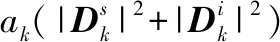
(16)

对优化函数的最优值而言,J(C)opt≠J*(C)opt,但这两个优化函数的最优解相等,都为Copt。

由于矩阵的迹具有非常良好的运算性质,下面将式(16)改写成矩阵乘积的求迹,可得

(17)

其中,记

(18)

通常情况下,矩阵A都满足SVD的条件,令A=UDVT,D=diag(σ1,σ2,σ3),σi为奇异值,U为左奇异向量构成的正交矩阵,V为右奇异向量构成的正交矩阵,则进一步可得:

J(C)=tr(CAT)=tr(C(UDVT)T)=

tr(CVDUT)=tr(UTCVD)=tr(C*D)

(19)

J(C)=tr(C*D)=

(20)

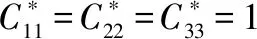
Copt=UVT

(21)

由此,在测量误差加权平方和最小的意义下,可通过上述SVD估计出最优姿态矩阵C*,进而得到3个姿态角。

3.4 QUEST算法

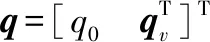
(22)

式中：qv×为矢量qv的反对称矩阵。

将式(22)代入式(17),可将优化函数自变量转换成q,即：

(23)

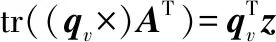
J(q) =

(24)

式中,矩阵M的形式如下:

(25)

观察可知,J(q)是不带一次项和常数项的二次函数,具有良好的求导性质。由于q为四元数,其具有隐含性质|q|=qTq=1。因此,考虑为带约束优化问题求解极值:

J′(q)=qTMq+λ[1-qTq]

(26)

利用矩阵求导的性质对式(26)求导,可得

Mq=λq

(27)

式中:M为4×4维矩阵,q为4×1维向量,λ为1×1维实数。显然,λ、q恰好为矩阵M的特征值、特征向量。将式(27)代入式(24),可得

J(q)=qTMq=qTλq=λqTq=λ

(28)

由于J(q)=λ,λ需要取最大特征值才能使目标优化函数J(q) 最大,此时特征值对应的特征向量即为最优姿态四元数qopt。

可以证明,矩阵M最大特征值λmax非常接近于1,这位迭代法的解算提供了很好的先验信息,因此,可以1为初始值基于牛顿迭代法对特征值λ进行迭代。矩阵的特征多项式f(λ):

f(λ)=det(W-λI)=λ4+τ1λ2+τ2λ+τ3

(29)

式中:τ1、τ2、τ3由矩阵M推导得到,属于已知量。接着,对f(λ)求一阶导可得:f′(λ)=4λ3+2τ1λ+τ2,即最大特征值λmax的迭代公式为

(30)

通常情况下,在经过2～4次迭代后,最大特征值λmax的精度就能稳定在一个非常高的水平。获得λmax后,即可基于矩阵等式Mq=λq,通过初等行变换得到最大特征值λmax对于的特征向量,即最优姿态四元数qopt。

3.5 线性估计算法[6]

原始Wahba问题构造的最优目标函数见式(13)。最小化式(13)等价于求下式的最优解C,C使得ek的绝对值之和最小:

(31)

式中:ek表示第k个误差项。理想情况下ek=0。

设某一观测矢量对如下:

(32)

(33)

C1、C2、C3是姿态矩阵C的列向量,q为C对应的四元数形式,则

(34)

同理,可得C2=P2q、C3=P3q,则

(35)

(36)

由此,最优目标函数可写成如下形式:

(37)

假设星敏感器无测量误差,导航星表也没有赤经、赤纬误差,即J*(q)=0,可得

(38)

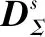
(39)

q†=qT=(q0,q1,q2,q3)

(40)

对于长方矩阵求逆,存在左伪逆矩阵、右伪逆矩阵和M-P伪逆矩阵3种类型。其中,M-P伪逆矩阵性质最好,但要求也最高,对于某个矩阵X,其M-P伪逆矩阵X†需要满足如下4个条件:

(41)

接着,对矩阵PΣD进行如下变换:

UDxP1+UDyP2+UDzP3

(42)

式中:UDx,UDy,UDz是3n×3的矩阵。将式(42)代入式(41)左侧,可得

(43)

令，

(44)

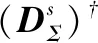
(45)

因此,式(39)可改写为

HxP1+HyP2+HzP3-q†=0

(46)

对式(46)进行转置操作并展开Hx,Hy,Hz,整理可得

(W-I)q=0

(47)

式中：矩阵W的各元素值见文献[6]。

上述结果是在理想情况下,即J*(q)=0时推导得到的,所以需要在式(47)中添加一个四元数误差项εq,进而可得

Wq=(1+ε)q

(48)

式中:ε为误差因子。显然,1+ε是矩阵W的一个特征值,且1+ε非常接近于1。因此,求解出矩阵W最接近1的特征值λopt及其对应的特征向量qopt即可。

4 仿真验证及分析

本节从数值仿真的角度对SVD定姿算法、双矢量定姿算法、LS定姿算法、QUEST定姿算法和线性估计算法的理论分析进行验证,仿真步骤如下:

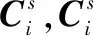
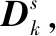
步骤3分别采用双矢量定姿算法、LS定姿算法和线性估计算法等求解姿态,并计算不同定姿算法的姿态角误差,双矢量定姿算法仿真时随机选取其中两个矢量信息对实现定姿;

步骤4计算不同算法定姿需要消耗的时间。多次重复上述步骤。

仿真使用Matlab 2018b,硬件参数为Interi7核心处理器,32G内存。

下面,以噪声标准差为1e-3和1e-5为例展开分析。噪声标准差为1e2和1e-4时的性能表现如表1和表2所示。

表1 算法的姿态角误差标准差

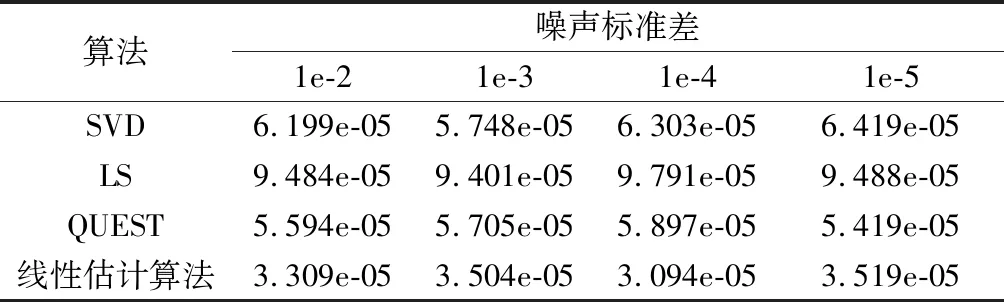
表2 算法的耗时图

图3可粗略看出,1e-3的噪声标准差下线性估计算法、QUEST算法和SVD算法的姿态角误差量集中性较好,基本都未超过3e-2的限值,这3种算法的误差量主要取决于恒星星光在天球系和星敏系中坐标矢量所受的噪声强弱;LS算法的姿态角误差量集中性稍差一些,主要分布在于±6e-2之间,该算法的误差量除了受恒星星光坐标矢量的噪声影响外,其算法本身的模型也对定姿精度产生了一定的限值,即该算法并不是最优的;双矢量定姿算法的姿态角误差量集中性最差,定姿效果最差,这主要是因为该算法在定姿过程中只用到了两个恒星星光的矢量信息对,所以对噪声非常敏感。归算仿真得到的定姿数据,1e-3的噪声标准差下不同算法的姿态角误差标准差如表1所示,随机生成的1 000组仿真实验中姿态角误差的详细分布情况如下。

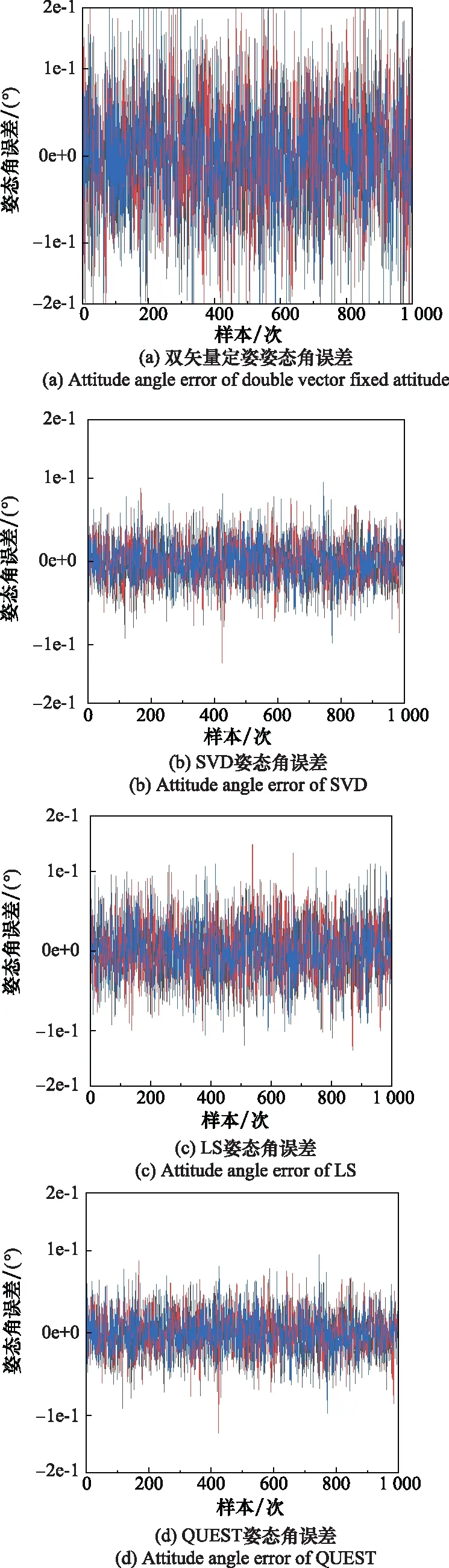
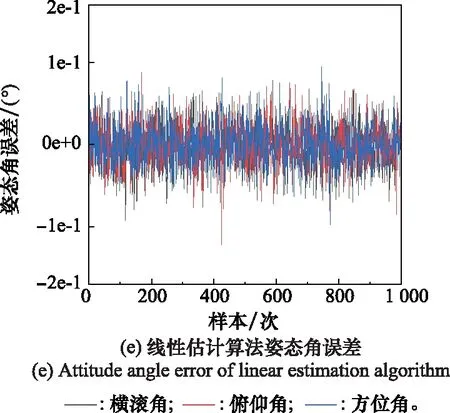
图3 1e-3标准差下不同算法的三轴姿态角误差Fig.3 Three-axis attitude angle error of different algorithms under 1e-3 standard deviation

同样地,图4可粗略看出,1e-5的噪声标准差下线性估计算法、QUEST算法和SVD算法的姿态角误差量集中性较好,基本都未超过6e-4的限值;LS算法的姿态角误差量集中性稍差一些,主要分布在于±8e-4之间;双矢量定姿算法的姿态角误差量集中性最差,定姿效果最差。归算仿真得到的定姿数据,1e-5的噪声标准差下不同算法的姿态角误差标准差如表1所示,随机生成的1 000组仿真实验中姿态角误差的详细分布情况如下。由表1可知,1e-3的噪声标准差与1e-5的噪声标准差下算法的性能表现一致,即双矢量定姿算法由于所利用的信息量少,定姿精度最差;LS算法由于并不是全局最优,定姿精度居中;其他3种算法定姿精度相当。

图4 1e-5标准差下不同算法的三轴姿态角误差曲线Fig.4 Three-axis attitude angle error curve of different algorithms under 1e-5 standard deviation

不同算法的计算效率主要取决于星光矢量的数目与算法本身的复杂度,与星光矢量坐标所受噪声强度无关,表2中数据处理结果也可看出。可以看出,LS算法的计算效率最低,基于处于1e-4 s的水平;线性估计算法的计算效率最高,基于处于4e-5 s的水平;QUEST、SVD算法的计算效率居中,基于处于7e-5 s的水平。由此可得,各算法的计算效率由低到高依次为LS算法、QUEST算法、SVD算法、线性估计算法。

综上所述,仿真实验表明双矢量定姿算法由于算法本身只采用了部分信息,其定姿精度最差;LS算法并不是全局意义上的最优姿态估计,其定姿精度次之;QUEST算法、SVD算法和线性估计算法定姿精度最高,得益于该3种算法都是对三轴姿态角的最优估计,区别在于推导方式不同而已。此外,各算法的计算效率由低到高依次为LS算法、QUEST算法、SVD算法、线性估计算法,即线性估计算法[6]的综合性能最好。

5 结 论

本文从理论上对星敏感器定姿SVD算法、双矢量定姿算法、LS算法、QUEST算法和线性估计算法进行了详细的理论推导。其中,线性估计算法充分利用伪逆矩阵的性质对二次四元数矩阵方程进行降次,有效建立了解决Wahba问题的线性理论。建立目标优化函数,利用星光矢量在天球系和星敏系中的坐标信息,对几种不同算法的定姿性能进行仿真对比分析。理论分析和仿真实验结果表明,线性估计算法和SVD、QUEST算法的定姿精度最高,线性估计算法的计算效率最高,即线性估计算法的综合性能最好。