基于路网信息辅助的多星编队系统SAR-GMTI动目标径向速度估计与重定位方法
2023-03-09李相海杨志伟廖桂生韩超垒
李相海, 杨志伟,*, 贺 顺, 廖桂生, 韩超垒, 姜 岩
(1. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071; 2. 西安科技大学通信与信息工程学院, 陕西 西安 710054; 3. 上海卫星工程研究所, 上海 200090)
0 引 言
多星编队雷达系统结合干涉合成孔径雷达(interferometric synthetic aperture radar, InSAR)技术与地面运动目标指示(ground moving target indication, GMTI)技术可执行高精度的测高、测速等重要任务[1-2]。动目标径向速度估计与重定位是SAR-GMTI研究的重点内容[3]。单星多通道系统可利用通道间的相干特性实现杂波抑制,通过进一步结合自适应匹配滤波(adaptive matched filtering, AMF),可估计得到目标径向速度[4]。我国的高分3号SAR卫星具有双通道GMTI模式[5-6],可满足高精度的动目标测速定位任务需求。多星编队系统可灵活构成多组有效基线,是实现更好的最小可检测速度(minimum detectable velocity, MDV)和更高的测速定位精度的重要途径[7]。文献[8]公开了超长沿航迹基线构型下的TerraSAR-X和TanDEM-X双星编队GMTI实验结果,极大程度地提升了目标的定位、测速和测向精度。对于多星编队系统,混合基线构型引入的地形干涉相位是制约系统GMTI处理性能的关键因素[9-10]。一方面,地形干涉相位使得杂波空间分布具有高程依赖性,杂波非均匀问题突出,进而导致杂波抑制性能恶化;另一方面,地形干涉相位与动目标径向速度干涉相位的耦合问题[11],导致动目标参数估计性能严重恶化。针对杂波非均匀问题,已有相关研究工作提出基于地形干涉相位补偿的稳健杂波抑制方法[12],此处不再赘述。针对动目标参数估计,文献[13]提出了一种多通道多像素联合处理方法,文献[14]利用目标相邻像素对相干信息进行高度补偿,可实现目标参数估计和定位功能,其测速精度高于单像素法。但是,动目标径向速度易导致成像位置发生偏移,目标真实位置与成像位置存在高度偏差,进而导致出现径向速度估计偏差。为此,文献[15]提出基于非线性阵列结构的干涉相位解耦合策略,文献[16]利用数字高程测量(digital elevation model, DEM)信息迭代补偿目标高程干涉相位。但是,这两种方法必须满足非线性阵列系统的约束条件,给系统设计和信号处理带来了挑战。
针对上述动目标参数估计难题,本文提出一种基于路网信息的迭代自适应匹配(knowledge based iterative AMF, KBI-AMF)算法,该算法可实现混合基线构型下的目标径向速度估计与重定位。算法核心是利用交通路网先验信息辅助补偿动目标成像位置与其真实位置之间的高程差,对补偿后的数据采用自适应匹配算法,进行动目标径向速度估计与重定位。为了提高算法的稳健性,进一步将重定位结果进行反馈并辅助目标高程补偿,采用迭代的方式获得最终的测速定位结果。此外,本文基于混合基线系统构型下的动目标信号模型,重点分析了线性阵列与非线性阵列构型下动目标高程干涉相位耦合对径向速度估计的影响。最后,基于仿真的多星SAR图像数据GMTI处理实验结果表明,本文方法能够有效消除目标高程的影响,在地形起伏场景中具有较好的径向速度估计和重定位性能,并且对线性和非线性阵列系统都具有很好的适用性与稳健性。
1 信号模型
假设由L个卫星构成多星编队系统,其观测构型如图1(a)所示,目标存在高程起伏情形时,观测场景示意图如图1(b)所示。将不同通道的数据排成列矢量z=[z1,z2,…,zL],其二元假设下的信号形式如下:
(1)
式中:zc=σc·ac⊙x表示杂波信号,σc表示杂波强度,ac表示杂波导向矢量,x表示杂波通道间的随机扰动,⊙表示Hadamard积;zT=A·a(h,vr)表示目标信号,A表示目标信号强度,a表示目标导向矢量;v表示白噪声。

图1 多星编队系统几何模型Fig.1 Geometric model of multi-satellite formation system
如图1(a)所示,星载编队雷达系统沿航迹基线与垂直航迹基线同时存在。沿航迹基线对目标径向速度敏感,垂直航迹基线对目标高程敏感。因此,混合基线构型下动目标干涉相位与地形干涉相位相互耦合[16],动目标信号的导向矢量可表示为
a(h,vr)=ac(h)⊙as(vr)=
[1,ejα1h,…,ejαL-1h]T⊙[1,ej β1vr,…,ej βL-1vr]T
(2)
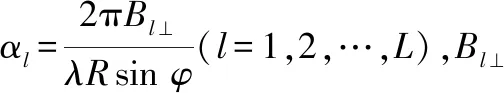
2 径向速度估计
2.1 干涉相位耦合问题
在混合基线构型下,针对动目标干涉相位耦合问题,可通过地形高程干涉相位估计与补偿实现GMTI任务[17]。然而,在实际处理过程中,动目标的真实位置未知,在利用目标成像位置所在邻域的杂波高程干涉相位对目标进行补偿时,难免存在补偿剩余:
A·a(Δh,vr)
(3)
式中:ac(hc)表示目标成像位置邻域的杂波导向矢量;(·)*表示取共轭;Δh表示动目标成像位置与真实位置之间的高程差。由式(3)可见,利用目标邻域内的杂波导向进行补偿,无法完全消除地形高程干涉相位的影响,由此引入的高程补偿误差会进一步导致径向速度估计性能恶化。仅考虑目标导向矢量a(Δh,vr)的干涉相位,可将式(3)中目标高程与速度的耦合关系表示为
(4)
式中:φl表示第1个空间通道与第l个通道的干涉相位。由式(4)可以看出,在混合基线构型下,目标速度干涉相位与高程干涉相位并非独立存在,在特定条件下,二者具有线性关系。因而,在自适应匹配处理过程中,目标高程补偿误差将转化为径向速度估计偏差。
对于线性阵列构型,不同空间通道的基线关系为固定比例,即αl/βl=κ,为固定常数。对应的相位关系满足φl(h,vr)=βl(κΔh+vr)由此可得目标导向关系满足:
a(Δh,vr)=as(κΔh+vr)
(5)
由式(5)可见,目标的速度导向和高程导向关系完全等效,高程补偿误差完全转化为径向速度估计偏差。因此,对于线性阵列构型,利用可空域自由度无法实现干涉相位解耦合。
对于非线性阵列构型,不同空间通道对应的比例系数αl/βl不同,与之对应的方位与俯仰维阵列导向结构不同。根据二维波达角(direction of arrival, DOA)估计理论,可采用二维最优波束形成的方式估计DOA参数[18]。因此,对于非线性阵列的干涉相位耦合问题,可利用空域自由度实现解耦合。式(3)中的目标导向同时存在速度与高度两个未知变量,需要将自适应匹配滤波算法[4]扩展为二维匹配估计:
(6)
式中:RC表示杂波协方差矩阵;(·)-1表示矩阵求逆操作。通常,为加快算法收敛速度,式(6)可采用坐标轮换法(coordinate descent, CD)交替优化求解[19]。利用空域自由度对速度和高度交替匹配搜索,即可得到径向速度的估计结果。
下面根据式(3)所给的信号模型,仿真分析目标高程补偿误差对径向速度估计的影响。设目标速度vr=3 m/s,目标信噪比为20 dB,杂波的杂噪比为20 dB,杂波通道幅/相误差为0.3 dB/3°,随机向量x=[x1,x2,…,xL]T服从复高斯分布,其他系统参数如表1所示。在仿真实验中,通过设置不同的目标高程补偿误差,进行100次蒙特卡罗实验,统计速度估计均方根误差(root mean square error, RMSE),并给出相应的变化曲线。
图2(a)和图2(b)分别是非线性、线性阵列构型下采用AMF方法时的速度估计均方根误差与目标高程误差的响应曲线。由图2可明显看出,目标高程干涉相位补偿误差导致一维AMF算法的估计偏差较大,并且成像位置与真实位置地形高程变化越大,导致的径向速度估计偏差越大。对比图2(a)和图2(b)可见,在非线性阵列构型下,二维AMF算法可实现速度-高程解耦合,其速度估计误差较小。但是,对于线性阵列系统构型二维AMF方法估计目标径向速度偏差较大,甚至失效。这是因为线性阵列构型下目标的速度导向与高程导向完全等价,高程补偿误差完全转化为径向速度估计偏差。
2.2 所提方法
针对混合基线构型下目标高程干涉相位耦合导致的径向速度估计偏差问题,通常可借助外部先验信息辅助来完成目标参数估计。文献[20]的研究结果表明,利用交通路网先验信息辅助可提高目标径向速度估计精度。其中,路网信息一方面可通过地理信息系统(geographic information system,GIS)获取,另一方面可直接利用SAR图像在线提取[21-22]。文献[16]提出了一种基于DEM先验信息辅助的最大似然估计(coordinate descent maximum likelihood, CDML)方法。CDML算法的核心思想是利用先验DEM信息补偿目标成像位置与真实位置之间的高程差,进而采用一维匹配滤波估计径向速度,最后根据径向速度估计与重定位结果重新补偿目标高程差,通过交替迭代处理得到最终估计结果。CDML方法可提高混合基线构型下的目标径向速度估计性能。但是,式(6)中的目标速度和高度两个变量存在耦合关系,当目标高程差较大时,径向速度估计偏差较大,进而导致CDML算法无法收敛。

图2 高程补偿误差导致的径向速度估计偏差Fig.2 Target velocity estimation bias caused by elevation compensation error
本文提出的KBI-AMF算法用于混合基线构型下的目标径向速度估计与重定位,其算法处理流程图如图3所示。首先,基于交通路网先验信息补偿目标真实位置与成像位置之间的高程差,然后利用自适应匹配滤波算法估计目标径向速度,最后将目标重定位的结果与路网信息结合,重新补偿目标高程差,通过迭代处理获得最终的目标径向速度估计与重定位结果。KBI-AMF算法的执行步骤如下。
步骤 1杂波抑制与目标检测。
混合基线构型下的杂波抑制首先需要通过地形干涉相位补偿来消除杂波的地形依赖性,补偿方法参见文献[12]。补偿后采用图像域的空时自适应算法进行杂波抑制[23],目标检测采用恒虚警(constant false alarm rate, CFAR)检测方式。
步骤 2在目标邻域内估计高程导向矢量。
依据地形缓变假设,目标检测位置邻域内的杂波具有近似相同的高程干涉相位导向。利用特征值分解的方式估计高程干涉相位导向:
(7)

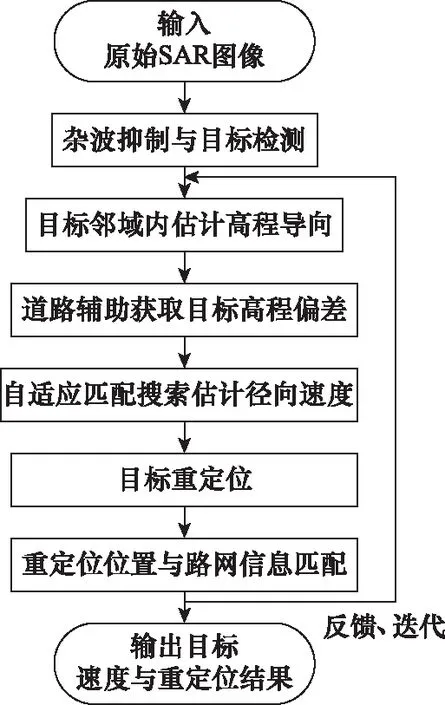
图3 本文算法流程图Fig.3 Flowchart of the proposed algorithm
步骤 3利用路网先验信息补偿动目标成像位置的高程差。

(8)
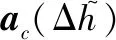
(9)
步骤 4利用自适应匹配滤波算法估计动目标径向速度。
利用一维搜索估计目标的径向速度:
(10)

步骤 5利用径向速度估计结果对动目标重定位。
根据式(10)中的径向速度估计结果对目标重定位:
(11)
式中:yD表示目标检测结果对应的方位位置;RT表示目标斜距。
步骤 6动目标重定位结果与路网位置信息匹配。
依据动目标成像理论,当目标速度与高度完全匹配时,目标重定位误差最小。所以,动目标重定位结果与路网位置误差最小的估计结果为有效估计:
(12)
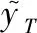
步骤 7考虑到实际处理过程中先验信息误差的影响,将步骤6中的重定位结果代入步骤3中,辅助估计目标高程差。通过迭代处理重复执行步骤3~步骤6,获得最终的目标径向速度估计与重定位结果。
当目标径向速度较大时,目标成像位置方位偏移较大,目标可能出现同时跨多条道路的情形,导致目标高程补偿存在较大高程差。由式(5)可知,高程补偿误差将直接转化为径向速度估计和重定位的偏差,进而导致本文算法的迭代过程无法收敛。此时,可利用目标回波的时域特性预估目标的运动参数。典型地,在SAR成像中常用距离走动补偿来实现动目标速度参数估计[24-25]。由目标速度的预估值对目标重定位,得到其真实位置所在的区域,用来辅助目标高程补偿,进而采用本文算法的处理流程获得更加准确的估计结果。
3 仿真验证
本节针对多星编队SAR-GMTI系统,利用基于真实地形场景DEM数据仿真的SAR图像数据验证本文方法的有效性。以星载四星编队SAR-GMTI系统为例,仿真参数配置为:轨道高度为700 km,卫星飞行速度为7 500 m/s,工作波长为0.03 m,脉冲重频为4 000 Hz,发射带宽为50 MHz,目标信噪比为20 dB,杂波的杂噪比为20 dB。仿真实验包含两个观测场景,分别仿真非线性阵列构型和线性阵列构型下的GMTI处理目标径向速度估计与重定位性能。详细参数如表1所示。

表1 雷达系统参数
3.1 仿真实验1
非线性编队构型的垂直基线分别为0 m、30 m、70 m、100 m。数据仿真结果如图4所示,其中,图4(a)为仿真场景的DEM图,图4(b)为原始幅度图,图4(c)为干涉相位图。从干涉相位图可明显看出,地形高程干涉相位沿距离和方位两维快速变化。在这类观测场景中,目标真实位置与成像所在位置的高程干涉相位存在较大差异,导致目标高程干涉相位补偿误差,进而影响径向速度估计性能。为验证本文方法的有效性,下面进一步给出GMTI处理结果。将本文算法的处理结果分别与一维AMF方法、CDML方法、速度估计克拉美罗界(Cramer-Rao bound,CRB)方法进行对比。其中,CRB由高斯假设下的Fisher信息矩阵求逆计算得到,详细计算过程可参考文献[26]。
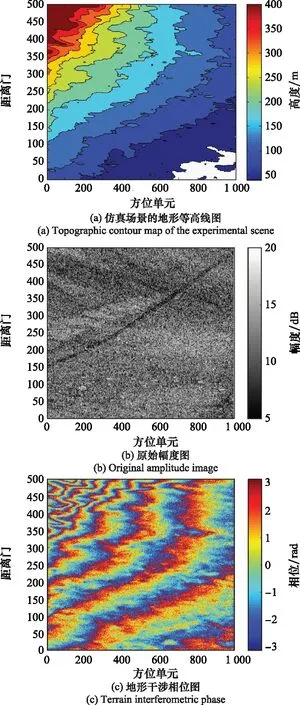
图4 场景1的多星SAR图像数据仿真结果Fig.4 Simulation result of multi-satellite SAR image
根据SAR-GMTI处理流程,对于混合基线构型首先要补偿地形干涉相位。本文采用二维频域补偿方法,可以避免由补偿过程导致的动目标干涉相位损失。然后,进行杂波抑制和目标检测处理,对于检测到的目标采用所提算法进行目标径向速度估计。道路先验信息事先已知,在实验中直接给出道路中心线的位置坐标,并假设其误差满足[-5,5]像素区间内的均匀分布。最后,在仿真实验中,通过设置径向速度不同的点目标,进行50次蒙特卡罗实验,统计速度估计均方根误差RMSE,并给出相应的变化曲线。对高程干涉相位补偿后的目标数据,分别利用一维AMF方法、CDML方法和本文方法进行速度估计,得到目标的径向速度估计结果,给出不同方法估计的RMSE与目标径向速度的变化曲线,如图5所示。
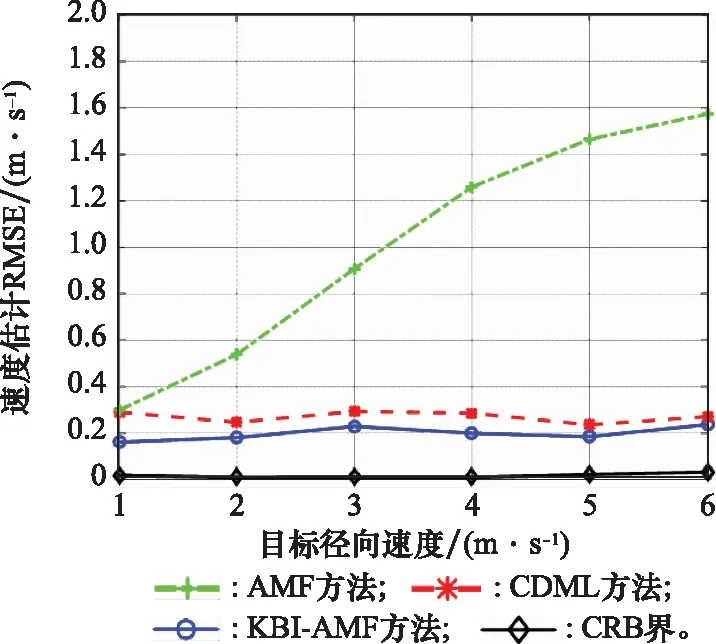
图5 非线性阵列构型RMSE随目标径向速度的变化曲线Fig.5 RMSE versus target radial velocity under nonlinear array configuration
由图5可见,将AMF方法直接用于混合基线构型下的动目标径向速度估计,存在较大的误差,并且目标速度越大,RMSE值越大。这是因为目标速度越大,其成像位置偏离真实位置越远,高程干涉相位补偿误差越大。从图4(a)和图4(c)可见,在本文的实验条件下,目标方位位置偏移越大,对应的地形高度差越大。仿真结果表明,目标地形高程干涉相位补偿误差导致AMF径向速度估计方法性能严重恶化,甚至失效。图5中,蓝色实线是利用本文方法获得的RMSE变化曲线,黑色实线是径向速度估计克拉美罗界。从图5可以看出,在非线性阵列构型下,采用CDML算法交替搜索和采用本文算法,可明显提升径向速度估计精度。
根据动目标成像理论,由径向速度的估计结果可对目标重定位。图6是根据径向速度估计值对运动目标重定位的结果,图6中蓝色圆圈标出了检测到的目标位置,黄色菱形标出了目标重定位的真实方位位置。由图6可见,动目标因径向速度使得成像后的方位偏离公路,经GMTI处理后,动目标被重定位到与其检测位置同一距离门的公路上。对比图6(b)~图6(d)明显可见,AMF方法受到高程干涉相位补偿误差的影响,测速重定位性能恶化,采用本文所提方法能够获得更高的目标径向速度估计精度。
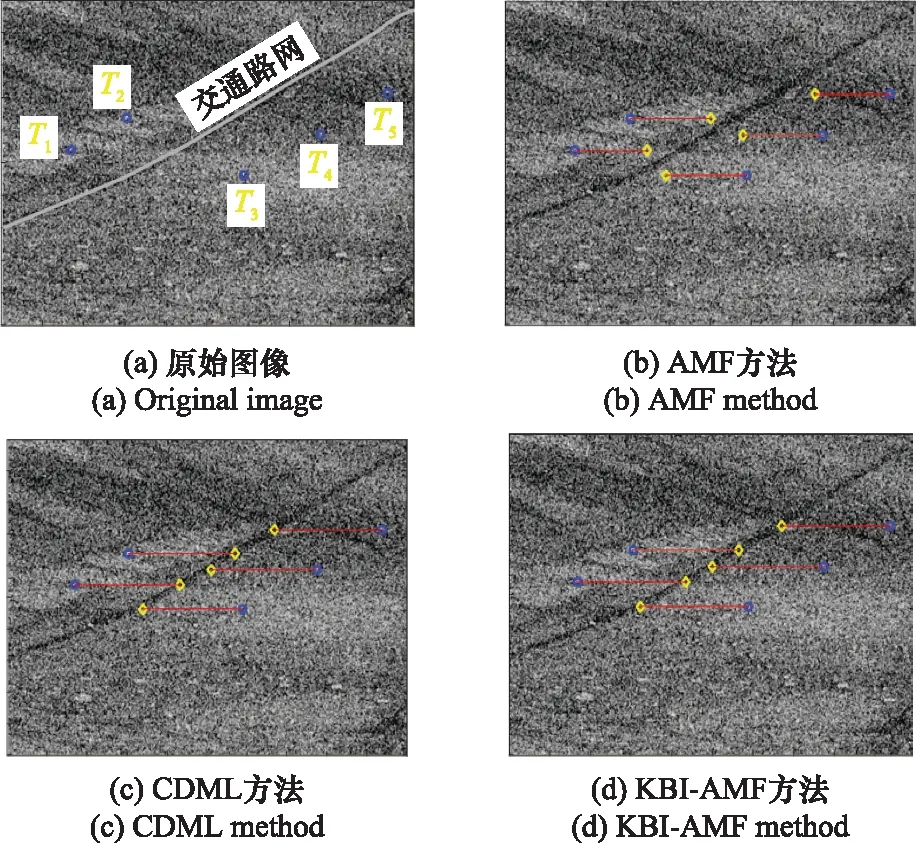
图6 非线性阵列构型下的目标重定位结果Fig.6 Target relocation results under nonlinear array configuration
3.2 仿真实验2
线性编队构型的垂直基线分别为0 m、30 m、60 m、90 m。数据仿真结果如图7所示,其中图7(a)为仿真场景的DEM图,图7(b)为原始幅度图,图7(c)为干涉相位图。
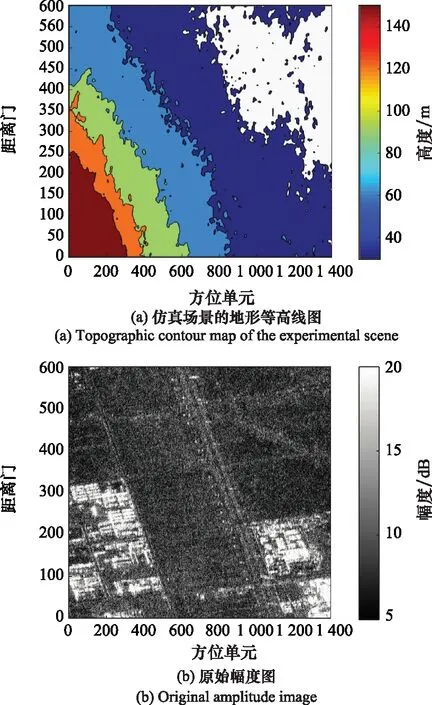
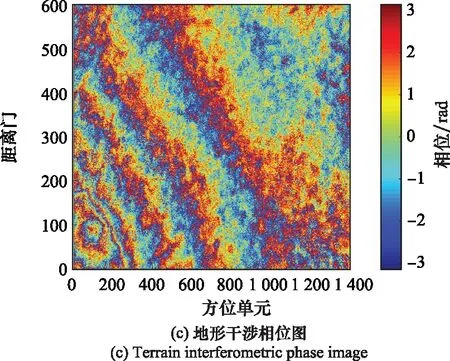
图7 场景2的多星SAR图像数据仿真结果Fig.7 Simulation result of multi-satellite SAR image
下面通过GMTI处理结果验证本文所提方法在线性阵列构型下的适用性与有效性。仿真实验通过设置径向速度不同的点目标进行50次蒙特卡罗实验,统计速度估计均方根误差RMSE,由不同处理方法估计的RMSE与目标径向速度的变化曲线如图8所示。

图8 线性阵列构型RMSE随目标径向速度的变化曲线Fig.8 RMSE versus with target radial velocity under linear array configuration
由图8可见,当将AMF方法和CDML方法直接用于线性阵列构型时,动目标径向速度估计存在较大的误差。这是因为AMF方法和CDML方法无法解相位耦合,高程干涉相位补偿误差直接转化为目标速度估计误差。并且,CDML方法的径向速度估计RMSE比AMF更大,因为当目标径向速度估计偏差较大时,高程干涉相位补偿误差也随之增大,从而导致CDML算法迭代过程发散。仿真结果表明,AMF方法和CDML方法在线性阵列构型下的径向速度估计方法性能严重恶化,甚至失效。图8中,蓝色实线是利用本文方法获得的RMSE变化曲线,相比于AMF方法和CDML算法,采用本文所提算法可显著提升径向速度估计精度。
从图7(b)可以看出,观测场景中存在多条道路,因此会导致速度估计的多值问题。本文利用径向速度的估计结果对目标重定位,进而将重定位结果与路网信息匹配。由此剔除存在多条道路时带来的虚假估计,得到最终的目标径向速度估计与重定位结果如图9所示。图9中,蓝色圆圈标出了检测到的目标位置,黄色菱形标出了目标重新定位的真实方位位置。图9(a)标出了目标检测位置,T1~T4为目标。其中,目标T4因径向速度较大,同时跨越两条道路。对比图9(b)~图9(d)的处理结果明显可见,AMF方法与CDML方法受到高程干涉相位补偿误差的影响,其测速重定位性能恶化,重定位位置明显偏离道路。采用本文所提方法进行GMTI处理后,目标被重新定位到与其检测位置同一距离门的公路上。特别地,从图9(d)中可以看出,目标T4同时跨越多条道路,采用本文算法处理后,可得到更准确的径向速度估计与重定位结果。
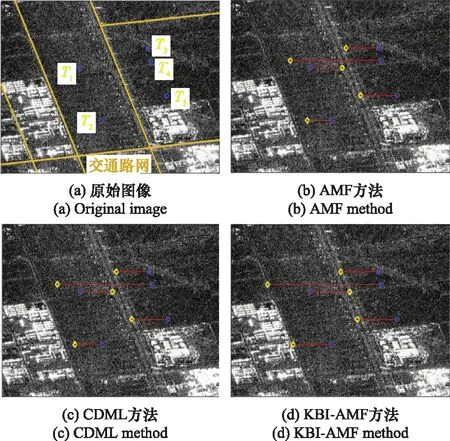
图9 线性阵列构型下的目标重定位结果Fig.9 Target relocation results under linear array configuration
综合实验1和实验2的结果不难看出,当多星编队SAR-GMTI系统存在混合基线时,目标的高程干涉相位补偿误差不可忽略,直接采用AMF方法估计目标径向速度会存在严重的估计偏差。在非线性阵列构型下,采用CDML算法交替搜索可缓解高程干涉相位补偿误差的影响,从而提升径向速度估计精度。但是,在线性阵列构型下,CDML方法无法解相位耦合,高程干涉相位补偿误差直接转化为目标速度估计误差,算法性能严重恶化。本文所提方法可有效消除高程干涉相位补偿误差的影响,且不受阵列构型的制约,具有很好的测速重定位精度。
3.3 算法稳健性分析
众所周知,基于先验信息的信号处理算法的稳健性受到先验信息本身的精度以及多源图像匹配程度的制约。近年来,多源图像配准和图像融合技术快速发展[27-28],相关研究表明,利用像素、强度、结构、纹理、轮廓、区域等多层次特征提取与融合[29],可实现像素级的图像融合精度[30]。为了进一步降低先验信息提取误差的影响,本文方法采取迭代处理,获得最终的目标径向速度估计与重定位结果。下面进一步验证本文所提方法的收敛性与稳健性。假设道路信息的随机误差服从[-10,10]像素区间内的均匀分布,采用本文方法进行50次蒙特卡罗实验,统计目标径向速度估计均方根误差RMSE,并给出速度估计RMSE与迭代次数的变化曲线,如图10所示。从图10可以看出,经过2~3次迭代,即可收敛,证明本文方法对路网信息误差具有很好的稳健性。

图10 目标径向速度估计RMSE随迭代次数的变化曲线Fig.10 RMSE of radial velocity estimation versus number of iterations
4 结 论
多星编队雷达系统在SAR-GMTI处理时面临着由混合基线引入的目标高程干涉相位耦合问题,严重制约动目标径向速度估计性能。针对该问题,本文提出了一种基于路网信息辅助的动目标径向速度估计与重定位方法,可有效解决由目标高程差导致的径向速度估计偏差问题,并且可同时适用于线性和非线性阵列构型。基于真实DEM的多星编队系统仿真SAR图像数据的GMTI处理结果表明,所提方法可有效消除高程干涉相位补偿误差的影响,提升多星编队混合基线系统在地形起伏场景下的目标径向速度估计与重定位性能,且不受系统构型的制约。特别地,对于地形存在突变的复杂地理场景,可通过高精度的DEM先验信息辅助,来提高目标测速定位精度。
