Position Measurement Based Slave Torque Feedback Control for Teleoperation Systems With Time-Varying Communication Delays

Xian Yang,Jing Yan,,Changchun Hua,,and Xinping Guan,

Abstract—Bilateral teleoperation system is referred to as a promising technology to extend human actions and intelligence to manipulating objects remotely.For the tracking control of teleoperation systems,velocity measurements are necessary to provide feedback information.However,due to hardware technology and cost constraints,the velocity measurements are not always available.In addition,the time-varying communication delay makes it challenging to achieve tracking task.This paper provides a solution to the issue of real-time tracking for teleoperation systems,subjected to unavailable velocity signals and time-varying communication delays.In order to estimate the velocity information,immersion and invariance (I&I) technique is employed to develop an exponential stability velocity observer.For the proposed velocity observer,a linear relationship between position and observation state is constructed,through which the need of solving partial differential and certain integral equations can be avoided.Meanwhile,the mean value theoremis exploited to separate the observation error terms,and hence,all functions in our observer can be analytically expressed.With the estimated velocity information,a slave-torque feedback control lawis presented.A novel Lyapunov-Krasovskii functional is constructed to establish asymptotic tracking conditions.In particular,the relationship between the controller design parameters and the allowable maximum delay values is provided.Finally,simulation and experimental results reveal that the proposed velocity observer and controller can guarantee that the observation errors and tracking error converge to zero.

I.INTRODUCTION

RECENTLY,bilateral teleoperators have drawn extensive attention due to application of space operation,robotic telesurgery and undersea exploration.In a typical teleoperation system,the human operator imposes force on the master manipulator based on visual or force feedback.It provides motion commands to the slave manipulator,which mimics the movement of master manipulator to handle operational tasks.The contact force is reflected back to the human operator.All these information are transmitted through communication channel.

During the past decades,coordinated control of bilateral teleoperation systems has been received great interests from both academic and engineering fields (see [1],[2] and the references therein).Most of the coordinated controllers for teleoperation systems rely on accurate velocity measurements,e.g.,[3]–[5].It is noted that the velocity information can be measured by Doppler velocity log (DVL) or fiber optic gyroscope (FOG).However,due to hardware technology and cost constraints,many commercial devices are not installed with DVL or FOG.On the other hand,even though the devices are installed with DVL or FOG,the velocity measurements are easily prone to failure due to manmade and ambient noises.Of note,inaccurate velocity measurements can lead to the chattering of distributed controllers.Therefore,it is quite necessary to shake off the reliance of velocity measurement units and design a velocity estimator for the coordinated control of teleoperation system.

In order to estimate the velocity information,we find thatvelocity observercan provide us with a promising solution.Particularly,the velocity observer regards position measurements as the feedback inputs,and thereby,the output-feedback method can be employed to estimate the velocity information [6]–[8].Inspired by this,a nonlinear velocity observer was developed in [9] to guarantee asymptotic convergence of the observation errors.However,the upper bound of velocity information in [9] is required to be pre-known.For that reason,two high-gain observers were developed in [10],[11] to estimate of the unavailable velocity information.Also of relevance,Huaet al.[12] designed a fast terminal sliding mode velocity estimation algorithm.In addition,Xiao and Yin [13]constructed a sliding mode observer for the unmeasurable velocity.In [14] and [15],dirty-derivative filters were developed to estimate the unmeasurable velocity information.Nevertheless,the high-gain observers and sliding mode observers are very sensitive to measurement noises,which would cause strong mechanical vibrations on the control system.With regard to this,a new methodology,called immersion and invariance (I&I),has been proposed to design velocity observers for Euler Lagrange systems.Instead of can celling the measurement noises,I&I methodology transforms the observer design as a problem of rendering the manifold attractive [16],[17],whose advantages including high robust to system uncertainty and strong tolerance to measurement noises.In [18],Karagianniset al.first incorporated the idea of I&I into the observer design,where the unmeasured states are estimated by rendering an appropriately selected invariant manifold attractive in the extended state space.Following by the above work,the I&I method was applied to estimate the robots’ relative distance in leader-follow formation control[19].As is well known,the main difficulty of applying I&I observer is the need to solve partial differential equation(PDE).In order to relax the requirement of solving PDE,an approximation technique was proposed in [20].However,the observer in [20] relies on the solution to certain integral,which cannot be always ensured in some specific situations.Meanwhile,the definitions of some observer functions are not clearly presented in [20].Also of relevance,a follow-up work[21] presented the explicit definitions of all functions (see equations (8) and (9) in [21]),nevertheless it specializes in the unknown function,which is not representative.

The position/force information between the master and slave site is transmitted through network.Due to the long distance and unexpected communication disturbance,there may be some delays between the time when the human operator sends the command and the time when the slave manipulator executes the command.The existence of even a small delay in the communication channel may cause instability of a whole teleoperation system[22]–[24].In order to guarantee passivity of bilateral teleoperator,a two-layer control architecture consisting of performance layer and passive layer was proposed in [25].Reference [26] extended the traditional timedomain passive controller to teleoperation systembased on four channel architecture.Reference [27] presented an adaptive neural synchronization control law for teleoperation system with consideration of unknown backlash-like hysteresis.The stable behavior of above works can be achieved under the constant delay assumption.Due to the complexity of communication network,however,the delays of data packets are time-varying.Under the presence of bounded time-varying delays,[28] proposed an adaptive neural network fixed-time controller for nonlinear bilateral teleoperator.The delay terms are treated as uncertainty,which is estimated by neural network.The effect of time-varying delay is eliminated by adaptive law in stability analysis.Reference [29] presented a T-S fuzzy model for single-master-multi-slave teleoperator and proposed leaderless control scheme.Although the stability of whole system can be achieved,the positions of master and slave converge to zero instead of tracking.

In this paper,a real-time tracking solution with consideration of only position measurement and time-varying delay is developed for slave-torque feedback controlled teleoperation system.To be specific,we present a velocity observer based upon the I&I methodology.Following the idea of I&I,the crucial issue is to make the off-the-manifold coordinate attractively.In order to achieve this goal,the mean value theorem is exploited to separate the observation error terms,and hence,all functions in our observer can be analytically expressed.Then,a slave-torque feedback control algorithm based on estimated velocity is proposed.The constructed Lyapunov-Krasovskii functional,which makes full use of delay information,is employed to establish delay-dependent convergence criterion.Main contributions of this paper lie in two aspects.

1) Velocity Observer Design:An I&I based velocity observer is developed,and meanwhile the sufficient conditions for exponential convergence are established.Compared with the existing nonlinear velocity observer [9],the proposed observer in this paper can remove the assumption on exact know ledge of the upper bound of speed.Different from the results in [20],all functions in our observer can be analytically expressed.The observation performance is experimentally validated on a three degree-of-freedom PHANTOM Premium1.5A robot.

2) Delay-dependent tracking condition:With the estimated velocity from observer,a slave-torque feedback control algorithm is designed to make the slave manipulator follow the trajectory of master manipulator.It is worth mentioning that,with the presented condition,the real-time asymptotic tracking performance can be guaranteed as compared with [29] and[30].Meanwhile,a delay-dependent convergence criterion is proposed based on the constructed Lyapunov-Krasovskii functional.Different from [28],the tracking solution in this paper provides the relationship between the controller design parameters and the allowable maximumdelay values.

II.SYSTEM MODELLING

We think that a teleoperator consists of two robotic subsystems,a master and a slave to exchange information.The task is to synchronize motion of the master and slave such that the slave mimics the behavior of the master.

where the subscriptmstands for master andsstands for slave,qi∈Rnis the joint position,are the acceleration and velocity,respectively;Mi(qi)∈Rn×nis the positive-definite inertia matrix;is the matrix of centripetal and coriolistorque;gi(qi)∈Rnrepresents the gravitational torque,Fh∈RnandFe∈Rnare human-operator force (torque) and environment force (torque),respectively;τi∈Rnis the applied torque.

The properties of teleoperation system are revisited below withi=m,s.

Property 1:The inertia matrix is lower and upper bounded,i.e.,there exist positive scalars ϱi1and ϱi2such that 0<ϱi1I≤Mi(qi)≤ϱi2I<∞.

then the following inequality holds:

Lemma 2 [32]:The matrix polynomial inequality

holds ford(t)∈[0,d2] if and only if there exist positive definite matrixSand skew-symmetric matrixPsuch that

Assumption 1:The human operator and the environment are passive,i.e.,

III.MAIN RESULT

A.Velocity Observer

For facilitation of stability analysis,the lumped-parameter mechanical system can be represented as port-Hamiltonian form.Then,the inertia matrix in (1) can be factorized as

System (3) satisfies the following properties [20].

The stability problems are now stated as follows.

Problem1:With only position measurements,we aim to design a velocity observer to estimate the velocity of bilateral teleoperation systems.This problem can be reduced to the estimation ofwith exponential convergence,which is equivalent to estimatexiwith regard to the relationship betweenandxiin (3).

Problem2:Considering the time-varying delay and unmeasurable velocity constraints,we aimto design a slave-torque feedback controller and give its delay dependent stability condition to guarantee real-time asymptotic tracking between master and slave robot.This problem is reduced to guarantee

Theorem1:Consider the teleoperation system(3).Suppose that the solutions of system(3) exist for allt≥0,then the velocity observer estimation error converges to zero exponentially.

Proof:The subscribeiis omitted.Consider the scaled observer error as

Based on (3) and (4),the error dynamic yields

According to Properties 5 and 6 ofS(y,x),the termS(y,x)x−S(y,ξ+β)(ξ+β)in (13) can be rewritten as

Based on (11),(13) becomes

Replace (5) in (16),which yields

We define Lyapunov function forz,ex,eyand (r−k) as

with

Using (5),the time derivative ofV2(r−k) is

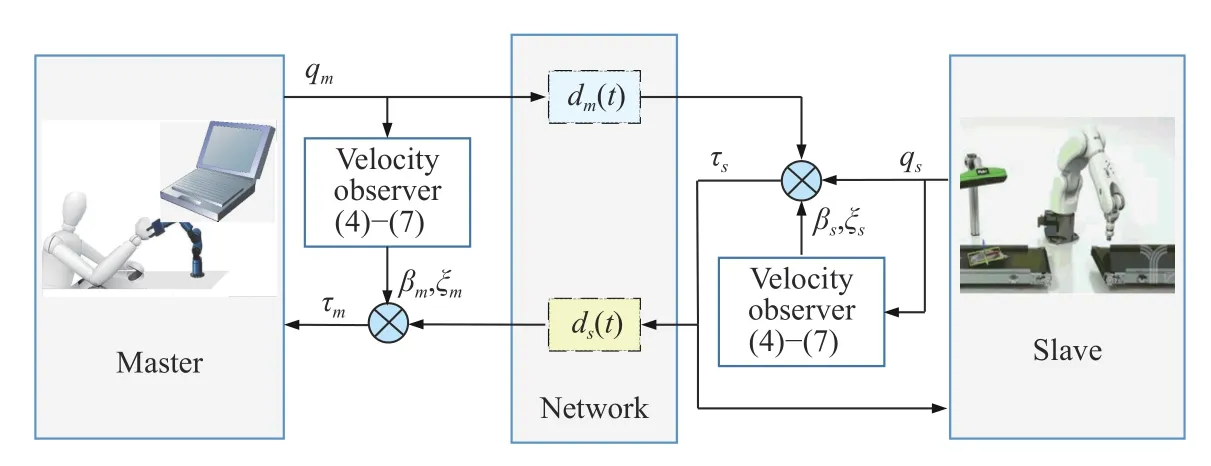
Fig.1.Construction relationship for the developed scheme.

Remark 1:We provide a detailed description of how to get(31).We have

B.Stability Analysis

The control objective is to drive the coordination errors to zero independently of the variable time-delaysdm(t) andds(t),i.e.,qm(t)−qs(t)→0.In this case,it is said that the manipulators synchronize.In this section,we will prove that the incorporation of the estimated velocities provided by the aforementioned observer (4)–(7) in the slave-torque feedback controller (see Fig.1),i.e.,

whereksis proportional coefficient, αmand αsare damping coefficients.For time-varying delaysdm(t) (the forward time delay,from the master site to slave site) andds(t) (the backward time delay,from the slave site to master site),there exist positive scalarsdi1,di2and µisuch that 0 ≤di(t)≤di2<∞ andfori=m,s.The bounds µmand µssatisfyµm+µs+µmµs<1.Denoted2,µ2and µ1asd2=dm2+ds2,µ2=µm+µs+µmµsand µ1=−µ2respectively.

Remark 3:In this subsection,we consider the stability problem of unmeasured velocity teleoperation system(1) with proportional position errors and delayed slave-torque feedback plus damping injection controller (42).For bilateral teleoperation system,the direct slave torque feedback control scheme is widely used.Compared with proportional error feedback control scheme,it is more challenging due to the complexity and difficulty for stability analysis.In Fig.1,the master positionqm(t)is transmitted from the master site to the slave site through time delaydm(t),and then transmitted from the slave site to the master site along with slave torque τs(t) through time delayds(t).The received delayed position signal at the master site can be described byqm(t−ds(t)−dm(t−ds(t))).

Theorem 2:Consider teleoperation system(1) with passive human force and environment force.If there exist positivedefinite matricesW1,Ze,Zs,Zi,Si,Qi,Ri1,Ri2,R3,skew-symmetric matricesPiand matricesYi,N,M,Xi=,i=1,2 with appropriate dimensions such that the following symmetric linear matrix inequalities hold:

where Property 2 is applied.

The first term in (48) can be rewritten as

and the eighth term in (48) can be rewritten as

Substituting (49) and (50) into (48),becomes

where the Young’s inequality is employed,ϵmand ϵsare positive constants.

From(46),one can calculate that the derivative ofV5is

Because 0 ≤dm(t)≤dm2,0 ≤ds(t)≤ds2and 0 ≤d(t)≤d2,(52) becomes

According to Jensen’s inequality,one can further obtain

According to Wirtinger inequality [35],the time derivative ofV6is

The time derivative ofV7is

where

with

According to integral inequality in [37],Ψ2(t) in (57) can be rewritten as

The following free-weighting matrices are considered:

Remark 4:In [27],[28],[30],by the designed control law,the position tracking error is guaranteed to converge to a small neighbourhood of the origin.In addition,the slave tracks a delayed information from master site,which gives rise to the position tracking errors.An asymptotic stability performance can be achieved with the proposed approach in [29].However,the position of master and slave converge to zero,i.e.,qm(t)→0 andqsi(t)→0 ast→∞.For bilateral teleoperation system,in order to complete the task better,the slave needs to be able to asymptotically mimic real-time movement of master,i.e.,qs(t)−qm(t)→0.Compared with the case in [28]where the delay terms are regarded as uncertainty,we establish a delay-dependent tracking criterion,which builds relationship between the controller design parameters and the allowable maximum delay values.The slave positionqs(t)asymptotically converge to the master positionq m(t) ast→∞.The stability conditions presented in Theorem 2 are in the linear matrix inequality (LM I) form and can be solved by Matlab LMI Toolbox.

IV.SIMULATION AND EXPERIMENT

In this section,simulation and experimental results are both presented to verify the effectiveness of our velocity observer.

A.Simulation Results

The dynamic of 2-DOF bilateral teleoperation system in (1)is given by (The subscriptsmandsare omitted.)

Fig.2.Human input force.

The stability performance is shown in Figs.3(a)−3(f).The control gains are chosen as αm=100, αs=20,ks=100.Whendm2=0.2,we obtain the allowable maximumvalue of backward delayds2=0.2578 by solving LM Is (43)−(45).We now analyze the teleoperators under two scenarios.In Scenario 1,the forward and backward delay are within the allowable maximum values,while in Scenario 2,the forward and backward delay are outside the allowable maximum values.With the proposed controller (42),the position trajectory of master and slave manipulator in Scenario 1 is shown in Fig.3 (a) (for joint 1) and Fig.3(c) (for joint 2),while the position trajectory in Scenario 2 is shown in Fig.3(b) (for joint 1) and Fig.3(d) (for joint 2).Figs.3(e) and 3(f) present master and slave velocities respectively.Clearly,the stability task in Scenario 1 can be achieved under variable communication delay and unmeasurable velocity.However,the tracking task in Scenario 2 is not achieved.This result demonstrates the effectiveness of our method.

The observation performance is shown in Figs.4(a)−4(f).For the master site,the position estimation obtained from the proposed I&I observer (4)−(7) is shown in Fig.4(a) (for joint 1) and Fig.4(b) (for joint 2).It is seen that the actual position of the joint is precisely estimated byafter a short period of time.As we can see from the enlarged part of Figs.4(a) and 4(b),the master position is successfully estimated at about0.1 s.The position estimation of the slave site is similar to the master site,and is omitted here.The errors between joint velocitiesand their observer estimation in Scenario 1 are presented in Figs.4(c) and 4(e),respectively,while the observation error in Scenario 2 are presented in Figs.4(d) and 4(f),respectively.In Figs.4(c)−4(f),the top figure is for joint 1 and the bottom figure is for joint 2.One can see that the estimation errors in Scenario 1 converge to zero.These results successfully demonstrated the conclusion in this paper that the precise estimation can be accomplished.

To validate our proposed observer,we also present a comparison with dirty derivative filter [14] and nonlinear velocity observer [9].Fig.5(b) plots the estimated master velocity(solid line) and actual one (dashed line) with nonlinear velocity observer [9].The graph in Fig.5(c) shows the time history of actual master velocity (dashed line) and its estimation(solid line) for dirty-derivative filter [14].From Figs.5(b) and 5(c),one can see that the dirty-derivative filter [14] and nonlinear velocity observer [9] suffer from the chattering phenomenon in the initial period of time.In contrast,the chattering with our velocity observer (as shown in Fig.5(a)) is much small.

B.Experiment

We describe some results of experimental investigation.The manipulator is Phantom Premium1.5HF robotic arm with 3-DOF positional sensing which is provided by Sen Able Technologies,Inc.The system is equipped with an ATI Industrial Automation Nano-17TM force/torque sensor.A real-time open-architecture control system is developed in order to achieve the full functionality of the robot.The platform that utilizes PHANTOM amplifier box uses a Quanser Q8TM data acquisition board and WinConTM/RTXTM real-time control system,which links with MATLAB Real-Time Workshop Toolbox.Each joint is attached with incremental rotary encoders to measure joint angles of the Phantom mechanism.Besides,six end-point generalized forces are provided by the force sensor in three Cartesian directions.The implementation of the controller and data collection run at the rate of 1 kHz.

The initial positions of master and slave manipulator in the joint space areqm(0)=[0.4999,0.2625,0.1241]T,qs(0)=[0,0.314,0.314]T,while the initial angular velocities of each joint is 0 rad/s.To be specific,the initial conditions and tuning parameters for experiment areThe control parameters are chosen as αm= αs=0.25,ks=8.

With the above setting,we apply the proposed observer and controller to the PHANTOM robot.The tracking performance is analyzed under two scenarios.In Scenario 1,the delay is within the allowable range,while in Scenario 2,the delay is outside the allowable range.The experimental results provided in Figs.6(a)−6(c) demonstrate the tracking performance in Scenario 1.It can be observed that the slave manipulator follows the trajectory of master manipulator.However,as shown in Figs.7(a)−7(c),the tracking task in Scenario 2 is not achieved.In view of these results,we can notice that the closed-loop teleoperators are asymptotically stable with our designed control law.

Fig.3.Stability performance.

Fig.4.Observation performance.

The velocity and the observer estimation are illustrated in Figs.8 (a)−8(f).There are some jitters at the actual velocity owing to noise.It is got from the velocity estimation as shown in Figs.8(a)−8(c) that the velocity of manipulator can be precisely estimated after a short period of time.The enlarged figures of Figs.8(a)−8(c) for some seconds are shown in Figs.8(d)−8(f).One can see that although the actual velocity suffers from measurement noise,the velocity observation performance is smooth.

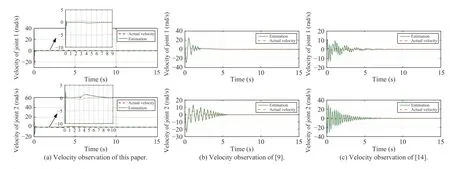
Fig.5.Comparison results.

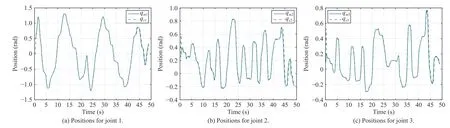
Fig.6.Experimental results for the trajectory tracking (Scenario 1).

Fig.7.Experimental results for the trajectory tracking (Scenario 2).

V.CONCLUSION AND FUTURE WORK

This paper investigates the stability problem for teleoperation systems under unmeasurable velocity and time-varying delay constraints.Specifically,a velocity observer based on immersion and invariance (I&I) technique is presented.A linear relationship between position and observation state is constructed,through which the need of solving partial differential and certain integral equations can be avoided.Meanwhile,the mean value theorem is exploited to separate the observation error terms,and hence,all functions in our observer can be analytically expressed.With the estimated velocity information,we develop a real-time convergence tracking solution.By employing the novel Lyapunov-Krasovskii functional,a delay-dependent condition is provided to build the relationship between control gains and the allowable bounds of delays.Both simulation and experimental results are presented to verify the effectiveness of our velocity observer and controller.The observer and controller are experimentally validated on a three degree-of-freedom PHANTOM Premium1.5A robot.Future work of this topic encompasses the issue of parametric uncertainties in system dynamics.

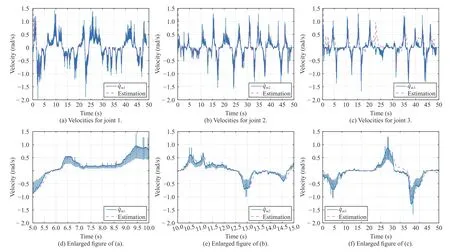
Fig.8.Experimental results for the velocity observer.

APPENDIX