Distributed Nash Equilibrium Seeking for General Networked Games With Bounded Disturbances

Maojiao Ye,,Danhu Li,Qing-Long Han,,and Lei Ding, Senior

Abstract—This paper is concerned with anti-disturbance Nash equilibrium seeking for games with partial information.First,reduced-order disturbance observer-based algorithms are proposed to achieve Nash equilibrium seeking for games with firstorder and second-order players,respectively.In the developed algorithms,the observed disturbance values are included in control signals to eliminate the influence of disturbances,based on which a gradient-like optimization method is implemented for each player.Second,a signum function based distributed algorithm is proposed to attenuate disturbances for games with second-order integrator-type players.To be more specific,a signum function is involved in the proposed seeking strategy to dominate disturbances,based on which the feedback of the velocity-like states and the gradients of the functions associated with players achieves stabilization of system dynamics and optimization of players’ objective functions.Through Lyapunov stability analysis,it is proven that the players’ actions can approach a small region around the Nash equilibrium by utilizing disturbance observer based strategies with appropriate control gains.Moreover,exponential (asymptotic) convergence can be achieved when the signum function based control strategy (with an adaptive control gain) is employed.The performance of the proposed algorithms is tested by utilizing an integrated simulation platform of virtual robot experimentation platform(V-REP) and MATLAB.

I.INTRODUCTION

IN recent years,distributed Nash equilibrium seeking,in which interacting entities try to minimize their own cost functions through neighboring communication,has become a research hotspot.For example,an average strategy fictitious play algorithm was proposed for repeated congestion games[1].The gradient play and a leader-following consensus protocol were employed for finding the Nash equilibrium[2].A distributed saddle-point strategy was proposed for two-network zero-sumgames to learn the Nash equilibrium[3].Switching communication conditions were further addressed for two-network zero-sum games [4].Both synchronous and asynchronous discrete-time methods were proposed for aggregative games [5].In addition,linear coupled constraints were addressed [6] and [7].Quadratic games were considered[8] and leader-following consensus protocols were employed for distributed estimation on both players’ actions and some values determined by the partial derivatives of objective functions associated with players,on the basis of which Nash equilibrium seeking algorithms were designed.High-order integrator-type games were considered [9],in which back stepping techniques were utilized to construct distributed Nash equilibrium seeking strategies.However,most of the existing results do not take system disturbances into consideration,which is non-realistic because many practical engineering systems are often subject to disturbances.

In engineering applications,system dynamics are affected by external disturbances and hence disturbance attenuation algorithms have received much attention [10]–[13].Typical disturbance attenuation techniques include extended state observers,equivalent input disturbance based estimators,nonlinear disturbance observers and unknown input observers,to mention just a few [14].For example,nonlinear disturbance observers have been widely adopted for disturbance rejection in practical systems including mobile wheeled inverted pendulums [15],air-breathing hypersonic vehicles [16],missiles[17],robotic manipulators [18] and knee joint orthosises driven by humans [19].In addition,sliding mode control was adopted for disturbance rejection of continuous stirred tank reactors [20].A sliding mode control algorithm was provided for servo systems associated with permanent-magnet synchronous motors [21].A sliding mode based observer was employed to achieve robust flight control of quadrotor vehicles [22].Moreover,disturbance attenuation algorithms have been broadly investigated for multi-agent systems.For example,the consensus problem of disturbed systems with secondorder agents was addressed by combining the dynamic gain strategy with a nonlinear disturbance observer [23].The containment control problem was studied via a nonlinear disturbance observer based disturbance attenuation method [24].Time delays and disturbances were considered,for which a sliding mode based algorithm was proposed for establishing the robust stability of a class of multi-agent systems [25].An adaptiveσ-modification technique was presented for disturbance attenuation of high-order multi-agent systems [26].Robust time-varying formation tracking control of disturbed uncertain multi-agent systems was achieved in [10].In [12],the distributed asymptotic consensus problem of high-order nonaffine multi-agent systems with nonvanishing disturbances was addressed.Reduced-order disturbance observer based approaches and radial basis function neural network based approaches were proposed in [27] and [28],respectively,to achieve distributed robust control of multi-agent systems.

Motivated by the significance of disturbance attenuation in practical systems,distributed Nash equilibrium seeking strategies were proposed based on extended state observers [29],[30].In the proposed seeking strategies,the disturbance and unmodeled dynamics are treated as an extended state of systems and observers are utilized to estimate them.An internal model based approach was employed to reject disturbances generated by specific external systems [31],[32].In addition,a distributed observer was utilized to approximate the disturbances in finite time [9] and a hyperbolic tangent function was utilized to dominant the disturbances [8].This paper intends to provide alternative ways to achieve disturbance rejection for distributed Nash equilibrium computation algorithms by utilizing reduced-order disturbance observers and signum functions.In comparison with the state of art,the contributions of this paper are summarized in the subsequent aspects.

1) This paper proposes reduced-order disturbance observer based approaches and signum function based approaches that achieve anti-disturbance distributed Nash equilibrium seeking for games with first-and second-order players.For both reduced-order based approaches and signum function based approaches,the disturbance observer/rejection module is of reduced-order compared with extended state observer based approaches [29],[30] and finite time observer based approaches [9].Moreover,the method [8] requires each player to distributively estimate not only all other players’ actions but also some values determined by the partial derivatives of players’ objective functions,which is not required in this paper.Therefore,compared with the methods [8],[9],[29],[30],the proposed methods require less computational cost.

2) Games with general cost functions are considered,which cover quadratic games [8] as their special cases.Furthermore,compared with [31] and [32],which assume specific disturbance models,the proposed approaches are not restricted to a specific disturbance model and require less know ledge about disturbances.

3) Through Lyapunov stability analysis,it is shown that the reduced-order disturbance observer based strategies can steer all players’ actions to approach a small neighborhood of the Nash equilibriumby appropriately adjusting control gains.In addition,the signum function based seeking strategies result in exponential convergence to the Nash equilibrium under the presented assumptions.

The rest of this paper is organized as follows.Section II provides the notations and preliminaries.The problem statement is presented in Section III.Main results are given in Section IV.Besides,Section V illustrates the performance of the presented algorithms via numerical studies.Section VI highlights the conclusion.

II.NOTATIONS AND PRELIMINARIES

Notations:The real number set is denoted as R .||z|| denotes the ℓ2-norm ofz.[zi]vecwherei∈{1,2,...,N} is defined as a column vector whose dimension isN×1 and theith element iszi.diag{ki} fori∈{1,2,...,N} is a diagonal matrix whose dimension isN×Nand theith diagonal element iski.diag{aij} wherei,j∈{1,2,...,N} gives a diagonal matrix whose dimension isN2×N2and diagonal elements area11,a12,...,a1N,a21,...,a2N,...,aN1,...,aNN,successively.A=[aij] is a matrix whose (i,j)t h entry isa i j.Given that matrixQis symmetric and real,λmin(Q)(λmax(Q)) stands for the smallest (largest) eigenvalue ofQ.maxi∈{1,2,...,N}{li} denotes the largest value oflifori∈{1,2,...,N}.The value of max{a1,a2}(min{a1,a2}) equals the larger (smaller) value ofa1anda2,which are real constants.IN×Nis an identity matrix with its dimension beingN×Nand 1N(0N) is a column vector with its entries being 1 (0).Moreover,⊗ is the Kronecker product.

Algebraic Graph Theory:A graph G is given by G=(V,Eg),in which V={1,2,...,N},Eg⊆V×V respectively are the node set and edge set.The edge (i,j)∈Egindicates that nodejcan receive information from nodei,but not necessarily vice versa.The in-neighbor set of nodeiis given as={j|(j,i)∈Eg}.A directed path is a sequence of edges of the form (i1,i2),(i2,i3),....A directed graph is strongly connected if for every pair of two distinct nodes,there is a path.Let A=[ai j] be the adjacency matrix in whichaij>0 if(j,i)∈Egandai j=0 if (j,i)∉Eg.In this paper,aii=0.Moreover,let D be the diagonal matrix with itsith entry beingThe nonsymmetrical Laplacian matrix associated with G is L=D−A [33].

III.PROBLEM STATEMENT

In the concerned game,Nplayers with labels from 1 toNare engaged and each playerihas a local objective functionfi(x):RN→R,in which x=[x1,x2,...,xN]Tandxi∈R is the action of playeri1For presentation simplicity,xi is supposed to be one-dimensional.It is worth mentioning that the presented methods and results are directly applicable to accommodate games with multiple dimensional actions..Moreover,for first-order players,playeri’s actionxiis generated by

whereuiis the control input of playerianddi(t) is the disturbance fori∈V.In addition,for second-order players,playeri’s action is governed by

wherevi(t) is the velocity-like state of playerifori∈V.Each playeriaims to minimize its own objective functionfi(x) by adjusting its own actionxi,that is

The objective of this paper is to design distributed control laws for games with first-order and second-order disturbed integrator-type players such that the players’ actions can approach the Nash equilibrium.

where x−i=[x1,x2,...,xi−1,xi+1,...,xN]T[2].

To facilitate the upcoming analysis,the following assumptions are made.

Assumption 1:Fori∈V,fi(x) is C2and ∇i fi(x) is globally Lipschitz with constantli.

Note that in this paper,we consider that the players only have partial information on other players’ actions.Hence,it requires a communication graph to realize their objectives.

Assumption 2:The directed communication graph among the players is strongly connected.

LetD0be a nonnegative diagonal matrix in which at least one of the diagonal elements are positive and H=L+D0.Then,the following result can be obtained.

Lemma 1 [33]:Under Assumption 2,there are symmetric positive definite matricesandof compatible dimensions such that

x,z ∈RN

Assumption 3:For,

where ∇i fi(x)=∂fi(x)/∂xiandmis a positive constant.

Remark 1:Assumptions 1–3 are widely adopted in the existing literature (see e.g.,[2],[5]–[7],[29]–[32]).Assumption 1 ensures that the players’ objective functions are sufficiently smooth.Moreover,the global Lipschitzness of ∇i fi(x) is employed to develop global results and it can be removed with the corresponding results degraded to be semi-global ones.Assumption 2 ensures that it is possible for the players to share information through neighboring communication,which enables the distributed estimation of the players’ actions.The strong monotonicity condition in Assumption 3 ensures the existence of a unique Nash equilibrium,on which[∇i fi(x∗)]vec=0N[29].Moreover,together with Assumption 1,Assumption 3 ensures that the Nash equilibriumis globally exponentially stable under the gradient play given by

which is the core idea behind the design of the seeking strategies [2].

IV.MAIN RESULTS

In this section,we first design distributed methods based on reduced-order disturbance observers for games with first-order and second-order integrator-type players,respectively,to realize anti-disturbance Nash equilibrium seeking.Then,distributed algorithms based on the signum function are developed for games with second-order players.

A.Disturbance Observer Based Distributed Nash Equilibrium Seeking for Games in Disturbed First-Order Systems

For first-order integrator-type players,each playeri’s actionxievolves according to (1).Motivated by [2],uiis designed as

Remark 2:The control law (8) is distributed as each player only utilizes its own information (e.g.,gradient and action information) and information from its neighbors in the communication network to update its own action.Moreover,the control design in (8) contains two parts:is used to compensate for the disturbances,and −∇i fi(yi) acts as a gradient like term,which would drive the players’ actions to optimize their own objective functions.

From(1) and (8),the closed-loop system is described by

To develop the convergence result,it is assumed that the disturbances have the following property.

Proof:See Appendix A for the proof.

Remark 3:Theorem1 indicates that for any initial condition,the presented algorithm(9) can steer all players’ actions to be arbitrarily close to x∗by suitably choosing control gains.To be more specific,θandτshould be chosen to be sufficiently large such that (24) and (25) are satisfied to establish the convergence results.Note that by the boundedness of x(t),d(t) andit can be obtained that z(t) is bounded according to (9).

Remark 4:It is worth mentioning that in the existing extended state observer based approaches [29],[30],the disturbance is treated as an extended state,by which (1) is written as

From the proof of Theorem1,it is clear that the ultimate errors are resulted from the time derivatives of disturbances.If the disturbances are constant,the method (9) would result in asymptotic stability results.To be more specific,the convergence result can be stated as follows.

Corollary 1:Under Assumptions 1–3 and constant disturbances,there exist θ∗>0 and τ∗>0 such that for anyθ>θ∗and τ >τ∗,the Nash equilibrium is globally exponentially stable by utilizing the control design (9).

This section gives disturbance observer based seeking strategies for first-order integrator-type games.Next,an extension to games with second-order integrator-type players will be provided.

B.Disturbance Observer Based Distributed Nash Equilibrium Seeking for Games in Second-Order Disturbed Systems

For second-order games,players’ actions are governed by(2).To achieve Nash equilibrium seeking distributively,the control input for playeri,i∈V is given by

By (2) and (12),the closed-loop systemis

To continue the upcoming analysis,the following assumption is made.

Proof:See Appendix B for the proof.

Remark 5:Theorem 2 suggests that one should firstly chooseθand τ1to be sufficiently large (such that (34) and(35) are satisfied).Then,with fixedθ,one should choose τ2to be sufficiently large such that (36) is satisfied to establish the convergence results for (13).Moreover,from Theorem 2,it can be concluded that under the above tuning rules,players’actions can be steered to be arbitrarily close to the Nash equilibrium.

In Theorem 2,it is assumed thatis bounded for x ∈RN,which may be restrictive to some extent.It is worth mentioning that this assumption can be easily relaxed as follows.

Assumption 6:Fori,j∈V,x is bounded given that is bounded.

Correspondingly,the convergence result can be stated as follows.

Remark 6:In Corollary 2,can be any positive constants,indicating that for any bounded initial condition,one can always find sufficiently large parameters θ,τ1,τ2to achieve distributed Nash equilibrium seeking with an arbitrarily small ultimate error.Moreover,comparing Theorem 2 with Corollary 2,one can see that the global result in Theorem 2 is reduced to be semi-global when Assumption 5 is relaxed into Assumption 6.

Note that similar to the results for first-order systems,the ultimate bounds in Theorem 2 and Corollary 2 are also resulted from the time derivatives of disturbances.Hence,if the disturbances are constant,the error signals would decay to zero as well.More specifically,the convergence result can be stated as follows.

In this section,reduced-order disturbance observer based distributed Nash equilibrium seeking strategies are proposed for games with second-order players.In Theorem 2 and Corollary 2,it is proven that the presented algorithm can drive x to be arbitrarily close to the Nash equilibrium x∗by suitably adjusting control gains.In the following,an anti-disturbance distributed Nash equilibrium seeking algorithm with asymptotic guarantees will be developed.

C.Distributed Nash Equilibrium Seeking for Games with Asymptotic Guarantees in Second-Order Disturbed Systems

To deal with anti-disturbance distributed Nash equilibrium seeking using signum functions,it is assumed that the disturbances have the following property.

Remark 7:Compared with disturbance observer based strategies,it can be seen that for the signum function based approach,the requirement on the disturbance is relaxed to some extent (see Assumptions 4 and 7).

To realize asymptotic Nash equilibrium seeking for games with second-order integrator-type players distributively,the control input is designed as

By (2) and (16),the closed-loop systemis

Then,we have the following result.

Theorem 3:Under Assumptions 1–3,5,and 7,there exists a θ∗>0 such that for each θ>θ∗,there exists a τ∗>0 such that for each τ>τ∗,players’ actions globally exponentially converge to the Nash equilibrium by (17).

Proof:See Appendix C for the proof.

Remark 8:Different from Theorem 2 which provides an ultimately bounded convergence result,it can be seen that the signum function based approach gives exponential convergence results.The main idea of the signum function based strategy is to employ a signum function to eliminate the side effects of time-varying disturbances.

In (16),the bounds of the disturbance terms are required.If they are not available,one may tune the control gain of the signum term online and adapt the control input (16) as

fori,j∈V.

Following the proof of Theorem 3,we have the following corollary.

Corollary 4:Under Assumptions 1–3,5,and 7,there exists a θ∗>0 such that for each θ>θ∗,there exists a τ∗>0 such that for each τ>τ∗,all players’ actions globally asymptotically converge to x∗and the adaptive control gains γifori∈V converge to some finite values by (18).

Proof:See Appendix D for the proof.

Remark 10:Compared with existing results,the proposed algorithms have the following advantages:

1) The proposed methods in this paper are of reduced order and require less computation cost compared with [9],[29],[30] while relaxing the conditions on disturbances.In [29] and[30],disturbances are treated as extended states.Hence,the dimension of system states is augmented.Moreover,the dimension of the state observer is in line with the augmented system.Similarly,the finite time observer involved in the seeking strategy [9] has the same dimension as the system state.Therefore,compared with [9],[29],[30],the proposed algorithms are of less dimension and hence save computational cost to some extent.In addition,it is assumed thatexist and are bounded [29],[30],while the signum function based algorithms developed in this paper only required i(t) to be bounded.

2) The proposed methods require much less communication and computation cost compared with the algorithms [8] while covering more general games.In the Nash equilibrium searching strategy proposed for quadratic games with disturbances[8],estimates on some value determined by the partial derivatives are needed,which results in high computation and communication cost for large scale games.Hence,compared with the methods [8],the proposed approaches require less computational cost.Besides,this paper considers players with general objective functions,which cover quadratic ones [8] as its special cases.Moreover,second-order players are taken into account in this paper while only first-order ones were addressed in [8].

3) Less know ledge on disturbances is required compared with [31] and [32].The results [31] and [32] considered games in systems with external disturbances generated by some differential equations of specific forms.Different from [31] and [32],we consider general disturbances without requiring any know ledge on the disturbances (except that they are bounded) for the signum function based algorithms.Furthermore,the seeking strategy [32] requires that the second smallest eigenvalue of the Laplacian matrix should be larger than some value determined by objective functions associated with players,which is not needed in the proposed algorithms.

V.SIMULATION STUDIES

This section demonstrates the performance of the proposed distributed algorithms by utilizing an integrated simulation platform of virtual robot experimentation platform(V-REP)and MATLAB.More specifically,four-wheeled (Mecanum wheels) omnidirectional vehicles (KUKA YouBot) shown in Fig.1,which are available in V-REP,are adopted.In the simulation,five KUKA YouBot mobile vehicles are involved in the game and the objective functions for the five vehicles are

By calculation,it is found that x∗=[1,1,−1,1,−1,−1,1,−1,0,0]T.In the following,the proposed algorithms (8),(12),(16) and (18) will be verified with x(0)=[−2.5,3.5,−4,2.5,−2,−4,−6,−4,−2.5,−0.5]T.Moreover,all the other variables are initialized at zero and the disturbance vector is considered to be d(t)=[2sin(t),2sin(t),2cos(t),2cos(t),4cos(2t),4cos(2t),4sin(2t),4sin(2t),6sin(3t),6sin(3t)]T.In addition,it is supposed that the vehicles can communicate through the graph depicted in Fig.2.Note that to simulate the proposed methods in V-REP,they are discretized.

Fig.1.The KUKA You Bot omnidirectional vehicle in V-REP.

Fig.2.The communication graph for the vehicles.

A.Disturbance Observer Based Distributed Nash Equilibrium Seeking for First-Order Disturbed Games

In this section,the algorithm(8) is simulated with=200,τki=200 and the results are shown in Fig.3.Fig.3 depictsxi1(t) versusxi2(t) fori∈{1,2,...,5}.It is found from Fig.3 that all vehicles’ positions approach a small region around the Nash equilibrium,thereby verifying the conclusion of Theorem1.

As a comparison,the proportional-integral (PI)-based extended state observer based approach in [29] is simulated.By utilizing the PI-based extended state observer,in (8) is generated by

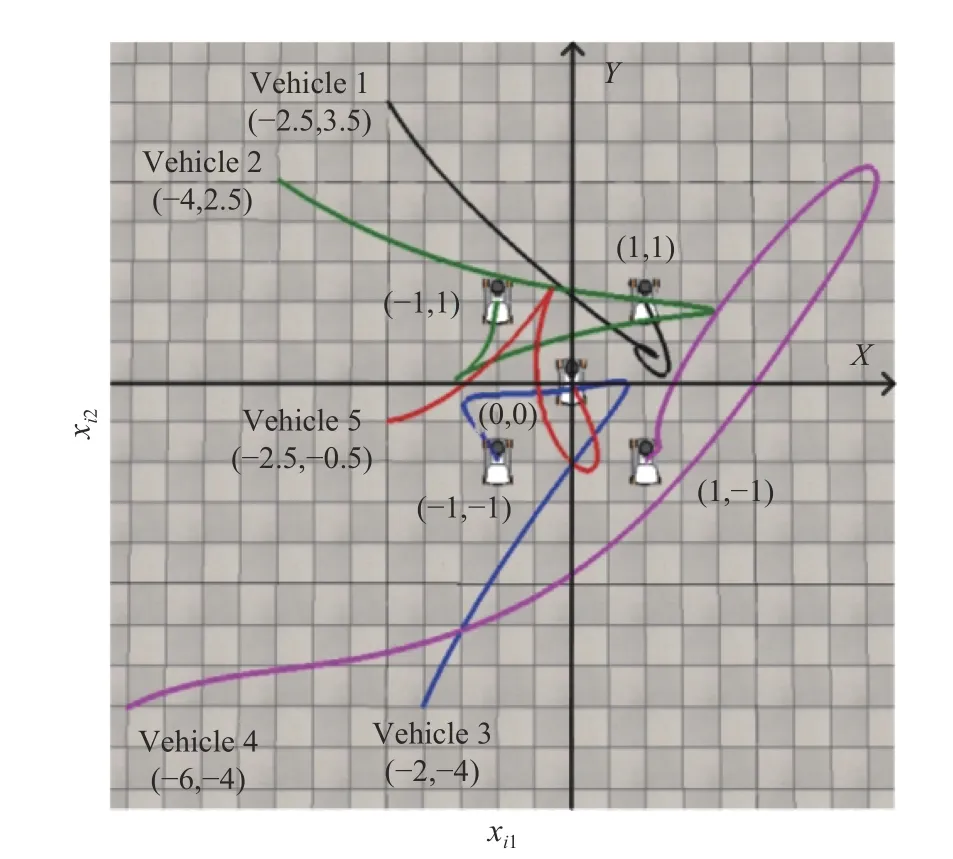
Fig.3.The trajectories of xi1 versus xi2 for i ∈{1,2,3,4,5} generated by (8).

instead,whereki1,ki2are positive constants.Correspondingly,withki1=5,ki2=25,=100,the simulation result is provided in Fig.4,which shows that all players’ actions can be driven to a small neighborhood of the Nash equilibrium.However,(19) requires each player to generate two variables (i.e.,to estimate disturbances while in (8),each player only needs to generate one variable (i.e.,zi).Therefore,the method (8) is of reduced order compared with the PI-based extended state observer based approach and thus reduces computational cost to some extent.

Fig.4.The trajectories of xi1 versus xi2 for i ∈{1,2,3,4,5} generated by the PI-based extended state observer based approach.

B.Disturbance Observer Based Distributed Nash Equilibrium Seeking for Second-Order Disturbed Games

In this section,the algorithm(12) is simulated with the corresponding results depicted in Figs.5 and 6,respectively.In the simulation,=310,τki1=2000,τki2=4500.Figs.5 and 6 plotxij,vijfori∈{1,2,...,5},j∈{1,2},respectively,from which it can be seen that the vehicles’ positions and velocity-like states approach a small neighborhood of the Nash equilibrium and zero,respectively.This verifies Theorem 2.

C.Signum Function Based Distributed Nash Equilibrium Seeking for Second-Order Disturbed Games

In this section,the algorithm(16) is simulated with τki=10,=100.The five vehicles’ positions and velocities are shown in Figs.7 and 8,respectively,from which it can be seen that the vehicles’ positions and velocity-like states respectively converge to the Nash equilibrium and zero.Hence,Theorem 3 is verified.

In addition,if the bounds of disturbances are unknown,(18)is adopted to update the vehicles’ positions.Correspondingly,the simulation results are given in Figs.9 and 10 with=100 and τki=7.Figs.9 and 10 showxijandvijfori∈{1,2,...,5},j∈{1,2},respectively,from which it is clear that the positions and velocities will respectively converge to the Nash equilibrium and zero.Hence,Corollary 4 is numerically verified.

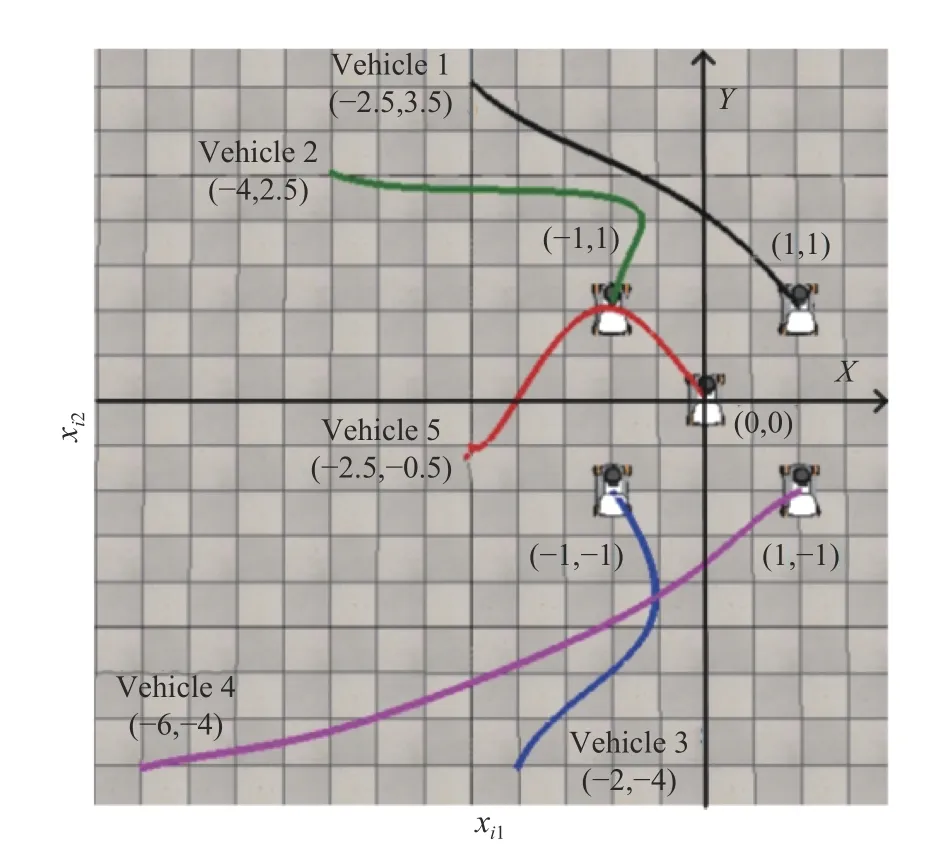
Fig.5.The trajectories of xi1 versus xi2 for i ∈{1,2,3,4,5} generated by(12).

Fig.6.The trajectories of vij,for i ∈{1,2,3,4,5} ,j ∈{1,2} generated by(12).

Fig.7.The trajectories of xi1 versus xi2 over time,for i ∈{1,2,3,4,5} generated by (16).

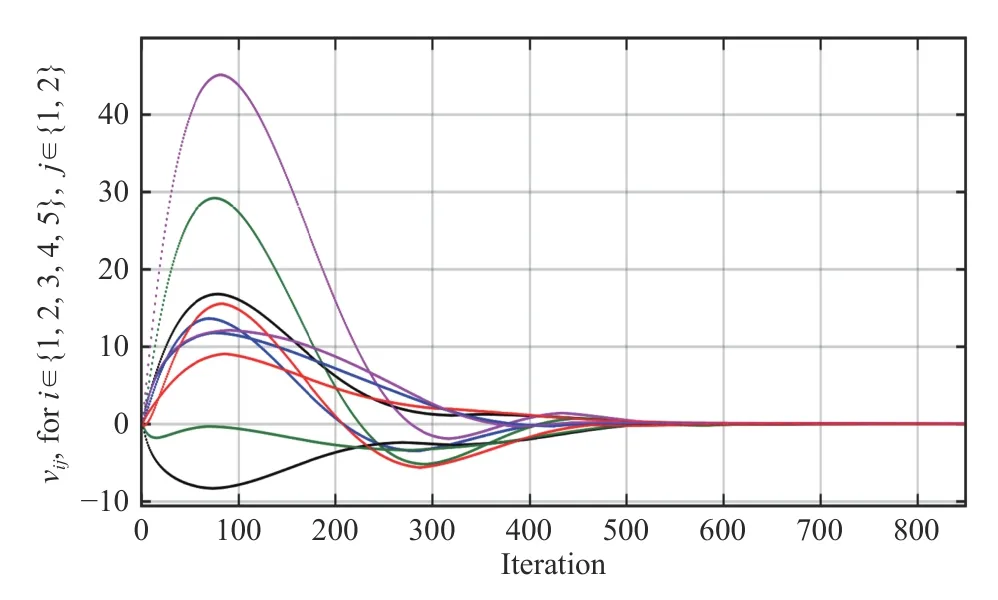
Fig.8.The trajectories of vij over time,for i ∈{1,2,3,4,5} ,j ∈{1,2} generated by (16).

Fig.10.The trajectories of vij for i ∈{1,2,3,4,5} and j ∈{1,2} generated by(18).

As a comparison,the robust integral of the sign of the error(RISE)-based extended state observer based approach [29],[30] is simulated.In the RISE-based approach,the observed disturbanceis generated by

in which βi1,βi2,βi3are positive constants.Correspondingly,the players’ action trajectories and velocities generated by the RISE-based algorithm are given in Figs.11 and 12,from which it can be seen that the players’ actions and velocities can be driven to the Nash equilibrium and zero,respectively.Nevertheless,by the RISE-based observer (20),each player needs to generate two more variables (i.e.,),which are not needed in the signum function based algorithm(16).Moreover,the RISE-based method requiresto be bounded,which is not needed in the signum function based algorithms.Therefore,compared with the RISE-based approach (20),the signum function based algorithm not only reduces computational cost but also relaxes the requirements on disturbances.

Fig.11.The trajectories of xi1 versus xi2 for i ∈{1,2,3,4,5} generated by the RISE-based extended state observer based approach.

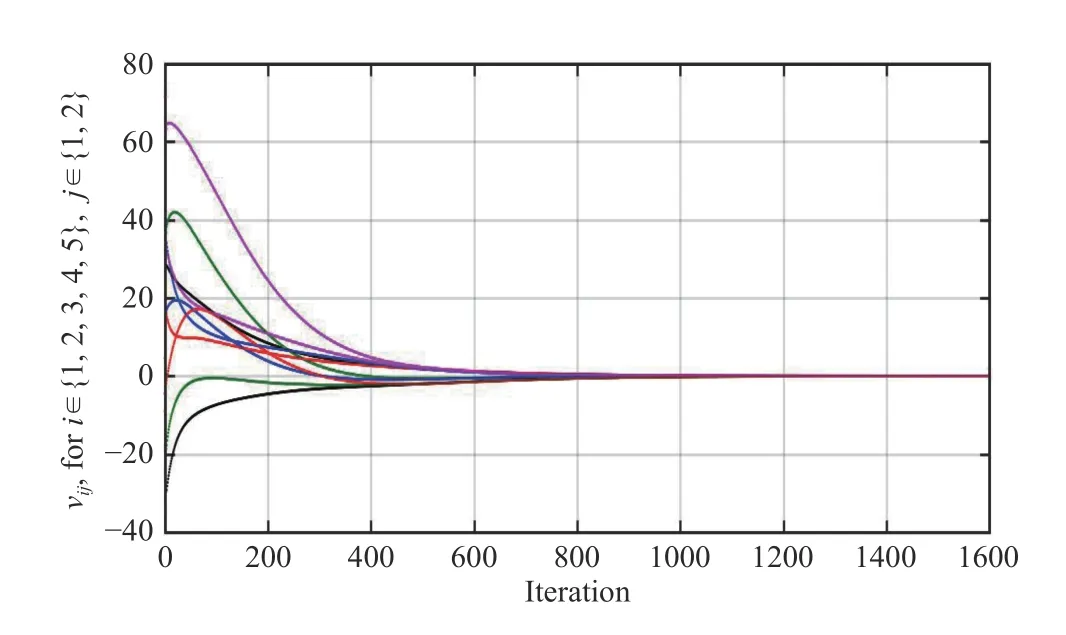
Fig.12.The trajectories of vij,for i ∈{1,2,3,4,5} ,j ∈{1,2} generated by the RISE-based extended state observer based approach.

VI.CONCLUSIONS

Anti-disturbance Nash equilibrium seeking algorithms for games with first-order and second-order disturbed distributed systems have been developed based on either a reduced-order disturbance observer or a signum function.It is theoretically proven that the actions of players can be steered to be arbitrarily close to the Nash equilibriumby an appropriate adjustment of control gains for the distributed reduced-order observer based approaches,and exponential (asymptotic) convergence can be further achieved when the signum function based strategy (with an adaptive control gain) is utilized.Event-triggered communication schemes (see e.g.,[35]) will be employed to relax the communication burden of the proposed algorithms with further consideration of communication delays (see e.g.,[36]) and control of players over networks (see,e.g.,[37]) in the future work.

APPENDIX A PROOF OF THEOREM 1