Data-Driven Control of Distributed Event-Triggered Network Systems

Xin Wang,Jian Sun,,Gang Wang,,Frank Allgöwer,and Jie Chen,

Abstract—The present paper deals with data-driven event-triggered control of a class of unknown discrete-time interconnected systems (a.k.a.network systems).To this end,we start by putting forth a novel distributed event-triggering transmission strategy based on periodic sampling,under which a model-based stability criterion for the closed-loop network system is derived,by leveraging a discrete-time looped-functional approach.Marrying the model-based criterion with a data-driven system representation recently developed in the literature,a purely data-driven stability criterion expressed in the form of linear matrix inequalities(LM Is) is established.Meanwhile,the data-driven stability criterion suggests a means for co-designing the event-triggering coefficient matrix and the feedback control gain matrix using only some offline collected state-input data.Finally,numerical results corroborate the efficacy of the proposed distributed data-driven event-triggered network system(ETS) in cutting off data transmissions and the co-design procedure.

I.INTRODUCTION

NETWORK systems have gained enormous attention over the last two decades,thanks to their widespread applications in diverse science and engineering disciplines [1]–[6].Such systems are usually composed of a group of interconnected subsystems distributed across large geographical locations,and information is exchanged through a public communication network.However,limited network resources,e.g.,bandwidth and energy of wireless transmitting nodes,make the control design challenging [7],[8].Traditional sampled data schemes,which are also known as time-triggered control,feature low computational overhead and easy deployment,but they often incur a considerable number of “redundant”transmissions occupying network resources [9]–[12].

Recently,for network systems,research efforts have centered around devising event-triggering transmission strategy that can rely on minimal communication resources while maintaining acceptable control performance.A decentralized event-triggered network system(ETS) using only local information was proposed for distributed control of continuous time network systems in [13] and [14],which was extended to discrete-time network systems in [15].Such decentralized ETSs are not optimal for distributed systems,because they did not exploit the interactions between adjacent subsystems in the design.By adding the neighbors’ information,a distributed ETS for multi-agent linear systems was designed in[1].In [16],a dynamic periodic distributed ETS was designed by introducing a dynamic variable into the static periodic distributed ETS [17],which can effectively reduce transmissions for each agent.In the context of networked control,continuous-time systems are controlled via digital computers,in which case one typically first discretizes the continuous-time system and works with the resulting discrete-time counterpart.As a matter of fact,few results on discrete-time ETSs for network systems are available in the literature.

On the other hand,all the above-mentioned ETSs are model-based,in the sense that they require explicit know ledge of system models for the controller design and implementation.Nevertheless,obtaining an accurate model of a real-world system can be computationally expensive and even impossible in many practical engineering situations.Furthermore,the obtained models are just too complex for classic control methods to be employed [18].An alternative approach,which is termed data-driven control,has recently attracted considerable attention.Data-driven control is aimed at performing control laws directly from measured data without requiring any steps of identifying real systems.Under this umbrella,various results have been presented,see summaries in e.g.,[19]–[22].By joining the data-based system parametrization in [23] and the model-based analysis method in [24],a data-driven stability criterion was developed for continuous-time linear systems with sampled-data control in[25],which has also suggested a data-driven controller.This data-driven framework has been extended to discrete-time sampled-data systems in [26].A data-driven resilient predictive controller against denial-of-service (DoS) attacks was developed in [27].Data-driven control of event-triggered continuous-time systems with constant delays was recently investigated in [28],which was then extended to the case of the discrete-time domain by [29].Thus far,it remains an unexplored territory to co-design data-driven distributed controllers as well as event-triggering transmission schemes for unknown discrete-time networked interconnected systems.

These developments have motivated our research on datadriven control of discrete-time networked systems under distributed event-triggering transmissions in this paper.In existing distributed ETSs [16],[17],only the relative state information of subsystem’s neighbors was used to design the ETS.The subsystem state used in designing the threshold of decentralized ETSs [13],[15] was not considered in [16] and [17].An undesired low triggering frequency may occur,when only the state errors between adjacent subsystems are considered and they are less than the local subsystem state,therefore considerably deteriorating the system performance.

In this paper,we develop a new dynamic distributed eventtriggering transmission strategy based on periodic sampling for discrete-time network systems,which generalizes the aforementioned decentralized and distributed ETSs.In addition,in terms of controller design and stability analysis,looped-functionals [30] have recently been shown competitive relative to common Lyapunov functionals that were used in existing distributed event-triggered control.By virtue of a discrete-time looped-functional,we derive a model-based criterion for distributed event-triggered control of network systems.By combining the model-based criterion and the datadriven representation of discrete-time linear systems developed in [23],a data-based stability criterion is established,which provides a data-driven method for co-designing the state feedback control gain matrix as well as the matrix in the event-triggering condition.

In succinct form,the contribution of this paper is two-fold,summarized as follows.

1) We develop a novel dynamic distributed ETS on the basis of periodic sampling for discrete-time network systems,where the triggering law only involves the discrete-time state information of each subsystem and its neighbor(s) at sampling instants;

2) We establish a model-and data-driven stability criteria for discrete-time network systems under the proposed distributed ETS using a tailored discrete-time looped-functional,along with model-and data-driven co-designing approaches of the controller and the ETS.

The remainder of the paper is organized as follows.In Section II,we introduce the network system under a distributed sample-data control strategy,as well as the data-based system representation.Section III provides the main results including model-and data-driven design methods of the controller for the network system with a novel distributed transmission scheme.Section IV validates the merits and effectiveness of our methods by numerical simulations.Section V summarizes this paper.

Notation:Throughout the paper,let symbols Rn,Rn×m,and N denote accordingly the sets of alln-dimensional real vectors,n×mreal matrices,and non-negative integers,respectively.For any integersa,b∈N,define N[a,b]:=N∩[a,b].Furthermore,we writeP≻0 (P0) ifPis a symmetric positive (semi)definite matrix,and [·] if its elements can be inferred by symmetry.Symbol blkdiag{···} represents blockdiagonal matrices,“ ∗”the symmetric terms in (block) symmetric matrices,and Sym{P} the sum ofPTandP.Finally,we use 0 (I) to stand for zero (identity) matrices of appropriate dimensions.

II.PROBLEM FORMULATION

A.Sampled-Data Control of Network Systems

Consider a network system consisting ofNdiscrete-time linear time-invariant subsystems (a.k.a.agents).These subsystems are coupled together and controlled by local controllers.A communication network is available to and shared by distributed systems.Each agent can communicate with its neighbors through the network,while the local controller can receive the neighbors’ information.The information flow can be described by an undirected graph G:={V,E,C},where V:={v1,v2,...,vN} is the set of nodes,and E ⊆V×V represents the set of edges.The matrix C:=[cij]∈RN×Nis the adjacency of G,constructed by settingcij=cji=1 if nodeviand nodevjare adjacent and they can share information between each other via communication channels andcij=cji=0,otherwise.Self-loops are not taken into consideration,i.e.,c ii=0 for alli∈N[1,N].

The state equation of subsystemiis given by

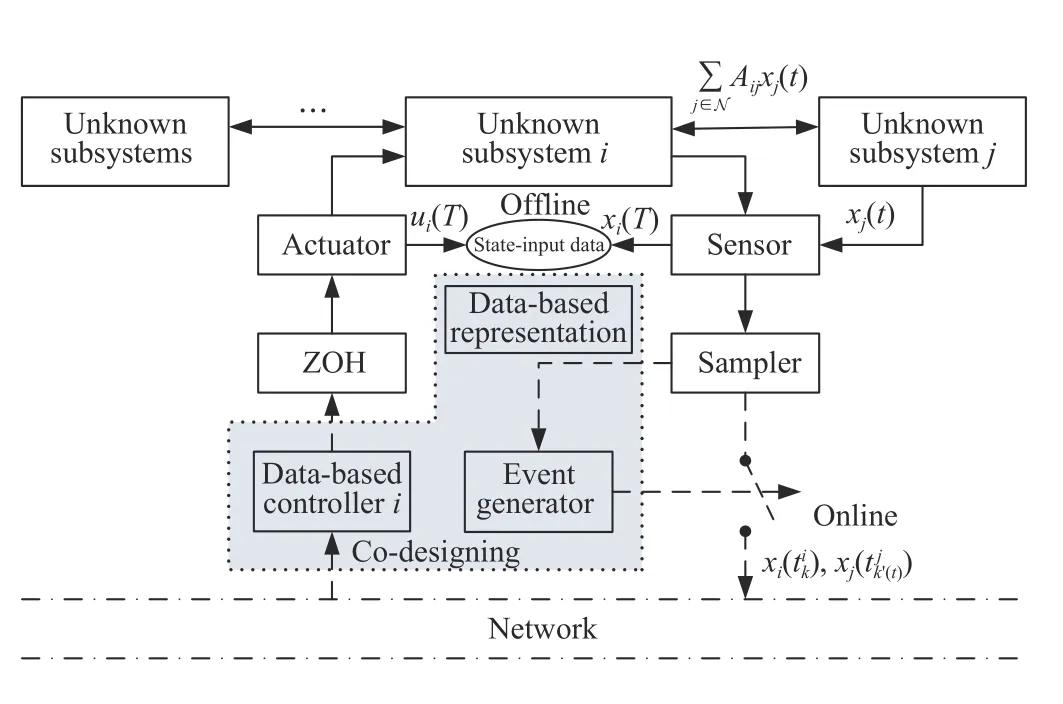
Fig.1.Data-driven networked control under ETS.

In fact,such network systems can model a wide range of applications,and they have been largely investigated in the literature,see e.g.,[2],[13],[31],[32].In contrast to the existing works,this paper focuses on a more challenging situation,in which the system matricesAi,Bi,andAi jare all assumed unknown.To save computation and communication resources,event-triggered transmissions between neighboring subsystems are considered.The overall goal of this paper is to develop purely data-driven solutions for co-designing the stabilizing control laws as well as the event-triggering protocols for all subsystems without explicit know ledge of the system matricesAi,Bi,Ai j.

It is assumed that during the closed-loop operation,the state of each subsystem is periodically sampled (e.g.,with a common period) in a synchronous manner,and the sampled state is transmitted to local and neighbors’ controllers only at event-triggered time instants.The event times of agentiare denoted bywherek∈N represents the order sequence of the transmission times and

In distributed control,each agent updates its own control input at event times it dictates by capitalizing on all information locally available as well as received from its neighboring agents.Specifically,at agenti,the local sampled stateand the statesof the neighboring agents are available,and the control input is computed using the linear feedback law

Remark 1 (Distributed controller):The proposed distributed controller in (3) has access to both the information of local agent and its neighbor(s) through the communication network.It has been discussed in [31] that traditional decentralized control strategy (3) withKi j=0 (using only local sampled states)incurs reduced design complexity and computational overhead.However,no exchange of information between adjacent subsystems may result in performance degradation and limit applications of the decentralized controller in network systems that contain large numbers of interactive nodes.From the perspective of system trajectories,the proposed distributed control strategy can achieve better performance than the decentralized one,as certificated by our numerical example in Section IV-D.

In the remainder of this paper,we discuss how to design stabilizing feedback controller gain matrices along with dynamic event-triggering strategies for system(4) or the interconnected linear systems (1),in a distributed and data-driven manner.We further develop theoretical analyses and performance guarantees for the resultant data-driven control solutions.

B.Data-Driven System Representation for Noisy Data

Through summarizing the local data,similarly to (4),the equation corresponding to global data collection is given as follows:

In practice,the noise is always bounded.It is thus reasonable to make the following assumption on the noise,which has also been used in e.g.,[25],[26].

Assumption 1 is a general form for modeling global bounded additive noise,which summarizes all local noises.WhenN=1,Assumption 1 is equivalent to the one used for centralized control systems by [23],[25],[33].

Based on (9) and Assumption 1,we may define the set of all matrices [A B] that are consistent with the measurements and the bounded noise as

Recalling [23,Lemma 4],it can be shown that ΣABcan be equivalently expressed as a quadratic matrix inequality (QM I)detailed as follows.

Lemma 1 (Data-driven system representation):The setΣABis equivalent to

Lemma 1 provides a purely data-driven parametrization of the unknown system(1) using only dataX,X+,andU.Note that such data are collected from the perturbed system(7),while we analyze the stability of the unperturbed sampled-data system(4).Introducing a disturbance in the presentation is to account for possible noise in pre-collected state-input data,rather than accommodating an explicit disturbance on the system.In order to guarantee the stability of (4) without relying on any know ledge of the system matrices,we need to achieve a stability criterion for all [A B]∈ΣAB.Note also that,in Fig.1,such data are collected offline in an open-loop experiment.In comparison,the sampling times {tk}kcome from a single closed-loop operation,which are independent of the open-loop data sampling.In the following section,we show the main result that provides a data-driven method for co-designing the distributed controllers and the ETS,where Lemma 1 is employed to describe the system matrices consistent with the data collected from (7).

III.MAIN RESULTS

In this section,we delineate our distributed dynamic eventtriggering strategy for discrete-time network systems in Section III-A.Model-based stability analysis of the distributed network system under the ETS is performed in Section III-B,while model-and data-driven co-design strategies of the distributed control and ETSs are studied in Sections III-C and IIID,respectively.

A.Distributed Dynamic ETS

We implement a discrete-time distributed event-triggering module to dictate the transmission timesfor each subsystemi,depicted in Fig.1.In such event-triggered network systems,it is assumed that all subsystems are sampled at time instantswherehis the sampling interval satisfying 1 ≤h≤h≤with given lower and upper boundsh,∈N.It should be mentioned that the sampling intervalhis not completely consistent with the step size of the discrete time system(1);that is,h>1 can be designed.Therefore,the trigger module is not required to detect the system state at every discrete timet.Building upon the distributed periodic ETS in [16],[17],[31],an event generator is introduced to determine whether the sampled data atneeds to be transmitted or not for each agent,capitalizing on the following criterion:

B.Model-Based Stability Analysis

C.Model-Based Controller Design

Theorem1 only provides an analysis method for event-triggered systems.We cannot obtain the controller gainKdirectly from solving the LM Is (15) and (16),due to thatKis coupled with the free matrixF.This part gives a new model-based condition for co-designing the distributed controllersKi,Ki j,and the ETS parameters based on Theorem1 while guaranteeing the stability.To this end,we start with an equivalently transformed system from(4).Assume thatGi∈Rn×nare nonsingular,and letxi(t)=Gizi(t).The system(4) is restructured as follows:

D.Data-Driven Controller Design

We are now ready to provide a data-driven method for codesigning a full structure of the block controller gainK,and all matrices Ωiof the distributed triggering scheme for system(4) with unknown matricesAi,Bi,Ai j.Motivated by [25],[26],the core idea is to replace the model in (1) with a datadriven system expression only using the measurementsFollowing this line,a data-based stability condition is obtained by combining the data-driven parametrization in Lemma 1 and the stability guarantee in Theorem 2.

Using the full-block S-procedure [38],inequalitiesare ensured for any [A B]∈ΣABif there is some ε >0 adhering to the following LM Is:

The Schur complement lemma guarantees that the inequalities in (37) and (38) are equivalent to (34) and (35).Subsequently,we can draw a conclusion that (34) and (35) at the vertices ofensure asymptotic stability of system(4)under the condition (12) for anyin(12) also converges to the origin.

Remark 4 (Conservatism):Theorem 3 offers a data-based stability criterion for unknown sampled-data control system(4),by which an allowable sampling intervalhcan be searched for only using state-input data.In our samplingbased ETS (12),a largerhmay lead to a lower communication rate thus to save network resources.For this purpose,three methods can be taken into consideration for reducing the conservatism of the data-based condition (cf.Theorem 3),which is beneficial for obtaining a greaterh.Firstly,selecting a suitable looped-functional that considers more system information is helpful for decreasing the conservatism of Theorem 3,due to the fact that Theorem 3 is built based on the model based condition in Theorem1.Note that the proposed loopedfunctional (18) only employs the system states and their single summations.According to the latest research results in[37] and [39] for single systems,less conservative stability conditions may be obtained if higher-order summations of the system states are used in constructing a proper looped-functional.Secondly,a tighter bounding technique used for estimating the nonlinear terms in (19) can enhance the feasibility of the condition;e.g.,choosing the summation inequality [36,Lemma 2] in the sense ofN>1 instead ofN=1 in this paper.Thirdly,leveraging prior know ledge on the system matrices or on the disturbance in data-driven system construction (cf.in Lemma 1) can significantly improve the performance of our data-driven method.For example,in the same spirit of [40] for single systems,a less conservative noise bound (cf.Assumption 1) can be reformulated if we assume that the disturbance satisfies a pointwise-in-time Euclidean normbound of the formfor allT=0,...,ρ−1.The detailed research about this topic can be found in [40].

Remark 5 (Comparison):Theorem 3 guarantees the asymptotic stability of all systems having [A B]∈ΣAB.Compared with the model-based condition in Theorem 2 for the unique[A B],our data-driven condition is more conservative,thus to inevitably supply smaller roomfor optimizing the transmission frequency and the system performance.Such a conclusion is certificated in Section IV through a numerical comparison,showing that our model-based method (cf.Theorem 2)ensures a lower transmission frequency than the data-based one (cf.Theorem 3) with the same triggering parameters,but results in faster convergence rates of the system trajectories.It should also be mentioned that Theorem 3 offers a condition for the unknown unperturbed sampled-data system(4).Our future works will focus on extending it to the case of guaranteeing an L2-gain performance on the perturbed system with bounded noise.

Remark 6 (Length of data):With the observation of LM Is(34) and (35),a merit of the data-driven method in Theorem 3 is that the dimensions of the corresponding LM Is are independent of the number of the collected state-input data (cf.Differently from the data-driven control of [33],our method is scalable to any length of data.Besides,it has been demonstrated in [40] that the guaranteed system performance may be improved by increasing the data length ρ in the data-driven control design,as more data can provide more accurate system description in Lemma 1.However,a higher computational complexity arises with the number of the data,which becomes challenging for large-scale network systems.This motivates us to balance the desired system performance and the number of data,which also constitutes our future research direction.

Remark 7:The distributed control strategy (3) and ETS (12)only require local information of the system,i.e.,the agent’s and its neighbors’ sampled states.However,data-driven control protocols in Theorems 3 are not fully distributed,which rely on the global information of the network graph,e.g.,when constructing the data-driven system representation in Lemma 1.For real network systems,it is possible to obtain the structure of the systems in advance and collect all stateinput data of the subsystems in offline.A practical numerical example is given in Fig.2 to demonstrate the effectiveness of the data-driven control method.

Fig.2.A network of coupled inverted pendulums.

IV.EXAMPLES AND SIMULATION

A network system consisting of three identical and coupled inverted pendulums is employed in this section to examine the proposed data-driven distributed event-triggered control methods;see Fig.2 for a pictorial description.Each subsystem(inverted pendulum) has the following dynamics,fori,j=1,2,3 andj≠i:

andg=9.8 m/s2is the acceleration due to gravity,m=1 kg is the mass of the pendulum,d=2 mis the length of the pendulum,andf=5 N/m is the spring constant;andNidenotes the number of neighbors of thei-th subsystem.The adjacency matrix C describing the communication graph is given as follows:

Upon discretization,we arrive at the following discrete-time linear system:

The proposed data-driven ETS (12) is then applied to system(40).In the following part,we examine the effectiveness of the proposed data-and model-based co-design methods.All numerical computations are performed using MATLAB,together with the SeDuMi toolbox [41].

A.Testing Data-Based Method

The proposed dynamic triggering scheme (12) is numerically tested using the system in (40),with the initial conditionx1(0)=[0.1,−0.1]T,x2(0)=[0.2,−0.2]T,x3(0)=[0.1,−0.2]Tover the time intervalt∈[0,300].The simulation results of all subsystems’ state trajectories (the top panel),triggered events(the middle panel),along with the dynamic variables(the bottompanel) are reported in Fig.3.Obviously,both the system states and the dynamic variables converge to zero,demonstrating the correctness of the proposed distributed data-driven triggering and control schemes.It should also be pointed out that only 34 measurements for the subsystem1,44 for the subsystem2,and 31 for the subsystem3 are sent to distributed controllers (3),while a total of 150 data were sampled for each subsystem.This validates the effectiveness of the data-driven ETSs in saving communication resources,while achieving distributed control of interconnected subsystems.

Fig.3.Trajectories of subsystems i and dynamic variables ηi(τiv) under data-driven ETS (12).

Remark 8 (Simulations for differentθi ):The numbers of transmitted data under the data-driven ETS (12) with different θiovert∈[0,300] are listed in Table I.As θiincreases from 2 to 1 04,the number of transmissions grows from 1 09 to a fixed value 154.The main reason is that our ETS (12)reduces to the static decentralized ETS [15] if θ →∞,which also confirms the statement in Remark 2.

TABLE I NUMB ER OF TRANSMITT ED DATA UNDER DATA-DRIVEN ETS (12) WITHDIFFERENT θi OVER t∈[0,300]

B.Testing the Model-Based Method

In this case,the matricesAandBof system(40) are assumed known.By Theorem 2 with the same triggering parameters as in Section IV-A,the fixed distributed controller gains and triggering matrices are computed as follows:

Then,under the above designed controller and ETS matrices,the trajectories of each subsystem and the extra dynamic variableare depicted in Fig.4 with the same initial states in Fig.3.Our model-based method (cf.Theorem 2) also ensures that all subsystems andconverge to zero.Note in the middle of Fig.4 that only 42 sampled data (1 3,1 3,16 for subsystems 1,2,3,respectively) are sent to the controllers,whose number is smaller than the number in the middle of Fig.3 (totaling 1 09).However,the settling time at the top of Fig.4 (aroundt=1000) is much longer than that in Fig.3(t=150).The main reason is that Theorem 2 has less conservatism than Theorem 3 at the expense of the system performance,which is discussed in Remark 5.

Fig.4.Trajectories of subsystems i and dynamic variables under model-based ETS (12).

C.Comparing With Centralized and Distributed ETSs

This part considers system(40) under the data-driven decentralized ETS (cf.(12) withand the data-driven distributed ETS (cf.(12) withUsing the same collected state-input data and the triggering parameters as in Section IV-A except for settingwe obtain the following controller gains and triggering matrices by Theorem 3 under the decentralized ETS:

D.Comparison Between Centralized and Distributed Controllers

This subsection explores the difference between the datadriven distributed controller (3) and the decentralized controller (cf.(3) withKi j=0) on the system performance of(40).To eliminate the impact of the triggering strategy on the system performance,we set.Therefore,the ETS (12) boils down to the periodic transmission scheme with sampling intervalh=0.02.Using Theorem 3 and the stateinput data of Section IV-A,we compute the decentralized controller gains as follows:

Fig.5.Trajectories of subsystems i and triggered events under data-driven ETS (12) with=0.

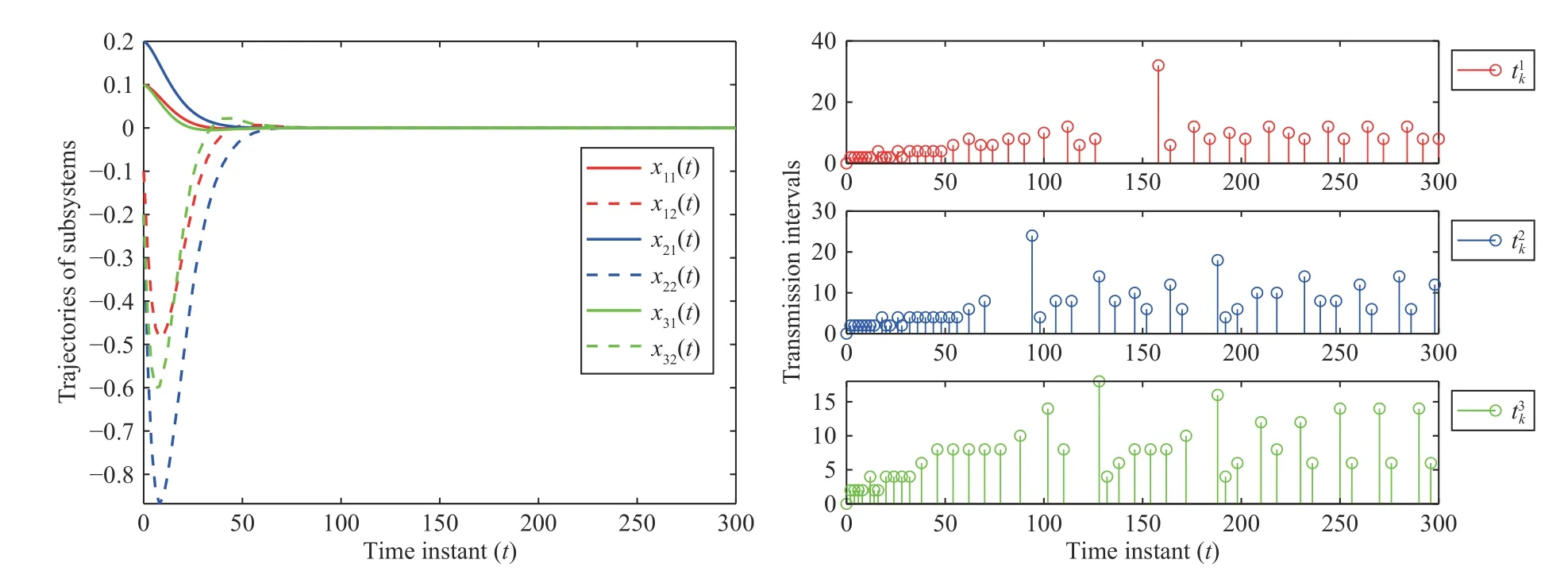
Fig.6.Trajectories of subsystems i and triggered events under data-driven ETS (12) with=0.

TABLE II NUMBER OF TRANSMITTED DATA UNDER DIFFERENT ETSS OVER t ∈[0,300]

And,the distributed controller gains are designed as

Employing the same initial points in Fig.3,trajectories of the system(40) under the above decentralized and distributed controllers and the periodic transmission scheme are depicted in Figs.7 and 8,respectively.Note that the settling time of system(40) in Fig.8 is aroundt=50,which is smaller thant=150 in Fig.7;namely,the distributed controller yields faster convergence rate than the decentralized one.This proves the correctness of the points made in Remark 1.

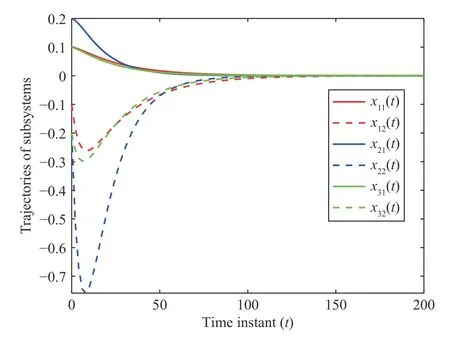
Fig.7.Trajectories of subsystems i under decentralized controller (3) with Ki j=0 and periodic transmission scheme.

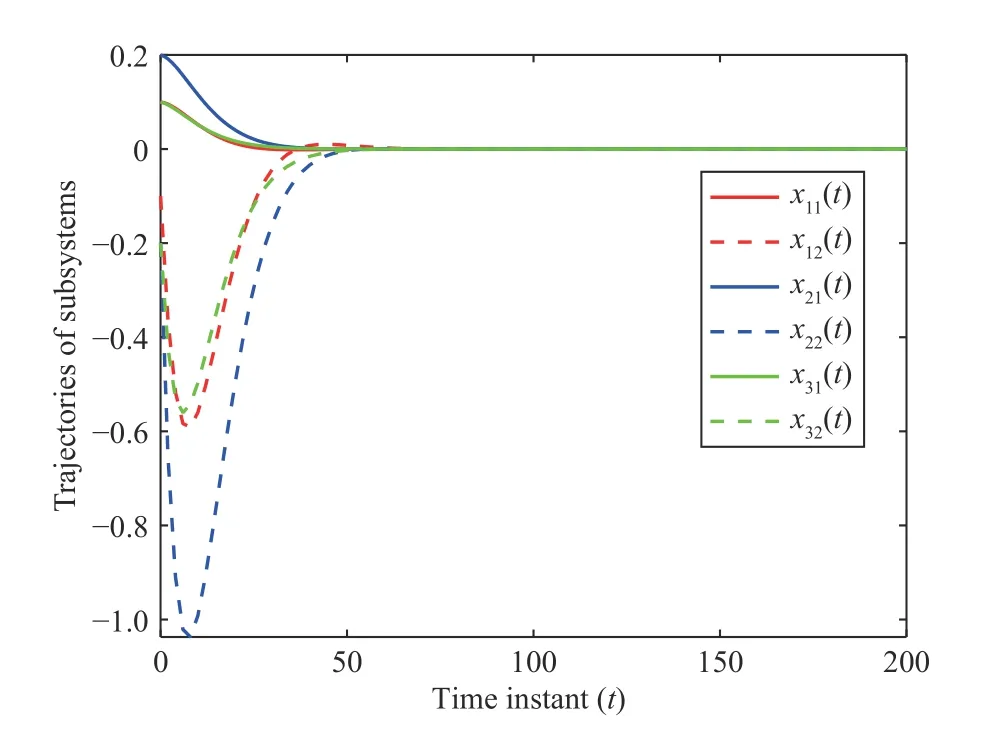
Fig.8.Trajectories of subsystems i under distributed controller (3) and periodic transmission scheme.

V.CONCLUDING REMARKS

This paper has considered distributed event-triggered control of interconnected discrete-time systems from a datadriven vantage point.Data-based system representation was developed,based on which a data-driven co-designing approach of the triggering matrix and the controller gain was provided.Closed-loop system stability under the proposed distributed data-driven event-triggered control scheme was analyzed leveraging a novel looped-functional.Finally,a numerical example was provided to corroborate the efficacy of the proposed ETS in saving communication resources,as well as the validity of our co-designing methods.Moreover,it was certificated by several numerical comparisons that the proposed data-driven distributed control strategy has better performance than existing decentralized and distributed strategies in reducing data transmissions while maintaining desired system performance.