Fixed-Time Stabilization of a Class of Strict-Feedback Nonlinear Systems via Dynamic Gain Feedback Control

Chenghui Zhang,,Le Chang,,Lantao Xing,,and Xianfu Zhang,

Abstract—This paper presents a novel fixed-time stabilization control (FSC) method for a class of strict-feedback nonlinear systems involving unmodelled system dynamics.The key feature of the proposed method is the design of two dynamic parameters.Specifically,a set of auxiliary variables is first introduced through state transformation.These variables combine the original system states and the two introduced dynamic parameters,facilitating the closed-loop system stability analyses.Then,the two dynamic parameters are delicately designed by utilizing the Lyapunov method,ensuring that all the closed-loop system states are globally fixed-time stable.Compared with existing results,the“explosion of complexity”problem of back stepping control is avoided.Moreover,the two designed dynamic parameters are dependent on system states rather than a time-varying function,thus the proposed controller is still valid beyond the given fixed time convergence instant.The effectiveness of the proposed method is demonstrated through two practical systems.

I.INTRODUCTION

FIXED-TIME stabilization control (FSC),which can ensure system trajectories to converge to zero before a given time regardless of the initial conditions,has been extensively studied in the past decades [1].This kind of control method was firstly formulated by Polyakov [2] in which the stabilization problem for uncertain linear plants is considered.It is shown that FSC can provide fast response speed together with a high control precision.Meanwhile,FSC is also able to deal with uncertain disturbances and inherent nonlinear dynamics.Because of these properties,FSC has been widely used in many mechanical and electromechanical systems [3]–[7].

The design of FSC can be divided into two categories: the time-dependent control and the state-dependent control.The time-dependent control is also called the pre-specified time control [8],[9],in which a time-varying function is used to regulate the converging rate.This function would converge to zero or infinity at the pre-specified time,causing the converging rate to be infinite.Although this kind of control can render system states to converge to zero at any time,the controller becomes invalid after the given settling time.To deal with this problem,a switching strategy has to be adopted which complicates the system control design [10],[11].

For the state-dependent control design,various technologies have been introduced in the existing literature.A hybrid control algorithm was introduced by combining a finite-time stabilizing control and a fixed-time attracting control in [2].To avoid the chattering regimes from hybrid controls,a nonhybrid control strategy with an involution operation sign was developed for both linear and nonlinear systems in [12].Through proposing a condition on a state-dependent function,Huaet al.[13] proposed a continuous FSC method for nonlinear systems.The implicit Lyapunov functions were introduced in [14] to construct fixed-time observers.Recently,Sunet al.[15] studied the fixed-time fuzzy tracking control problem for a class of unknown nonlinear systems.The fixed-time stabilization problem for linear systems with input delay was also studied in [16].However,it should be noted that the control structures of the aforementioned results all possess complicated forms which are not easy to implement.

The dynamic gain control approach has been widely used to solve the stabilization problems of nonlinear systems.This approach is able to cope with system uncertainties with the desired control performance guaranteed.With the help of dynamic gain control approach,the stabilization problems were solved in [17]–[21].It is shown in [17]–[21] that the control designed by the dynamic gains has a simple linear form which can greatly simplify the controller design.This motivates us to design FSC control method for uncertain nonlinear systems by using the dynamic gain control approach in this paper.In particular,the main contributions of this paper are summarized as below:

1) The proposed controller consists of two dynamic parameters and has a simple quasi-linear form.The two dynamic parameters are delicately designed by utilizing the Lyapunov method,ensuring that all the closed-loop system states are fixed-time stable.Compared with existing results,the “explosion of complexity”problem of back stepping control [9] is successfully avoided.

2) The designed controller can keep operating beyond the given fixed-time instant without any control strategy switching.This is different from the prescribed-time control methods in [9] and [11],where a time-varying function is employed to regulate the system performance.Our controller is particularly useful to cope with the case when the pre-specified time is not accurately determined.

The rest of this paper is organized as follows: Section II formulates the fixed-time stabilization problem for the strict feed back nonlinear system,while Section III details the design of the control method and analyzes the system performance.After that,the proposed control method is verified in Section IV through two actual systems.Finally,Section V gives the conclusion remarks.

II.PRELIMINARIES AND PROBLEM FORMULATION

Consider the strict-feedback nonlinear system

wherex=(x1,x2,...,xn)T∈Rnis the system state,andu∈R is the system input.The initial time instant is set as 0,and the initial system state is denoted asx(0) .f1(·) tofn(·) are unknown nonlinear functions satisfying the following assumption [22],[23].x=(x1,...,xn)T∈Rn

Assumption 1:For any,it holds that

fori=1,2,...,n,wherecis a positive constant.

System(1) under Assumption 1 is a typical strict-feedback nonlinear system which has been widely studied.For example,its asymptotic stabilization problems have been solved via the dynamic gain feedback control method [21],[23],[24] or the back stepping design method [25],[26].The fixed-time stabilizing problem was also studied in [27]–[29] through back stepping design method.This paper will develop a dynamic gain control method to achieve fixed-time stabilization whose definition is given below:

Definition 1 (Globally Fixed-Time Stable [2],[30]):Consider

wherex(t)∈Rnis the system state,andg(·):Rn→Rnis a continuous function satisfyingg(0)=0.The initial time instant is assumed as 0 and the initial state is denoted asx0∈Rn.System(3) is globally finite-time stable at the equilibriumx=0 if it is Lyapunov stable and finite-time attractive,i.e.,there exists a local bounded functionT(x0):Rn→R+∪{0}such thatx(t;x0)=0 for allt≥T(x0),wherex(t;x0)is the solution of (3) with the initial statex0∈Rn.The functionT(x0) is called the settling ti me function.It is s aid that system(3) is globally fixed-time stable at the equilibriumx=0 if it is globally finite-time stable and the settling time functionT(x0)is globally bounded by some positive constantTmax>0,i.e.,T(x0)≤Tmax,∀x0∈Rn.The constantTmaxis called the setting time.

With the above definition in mind,the control objective of this paperis to design the control signalusuch that system(1)is globally fixed-time stable at the equilibriumx=0.To this end,the following two Lemmas are given for the controller design later.

Lemma 1 ([31]):Let 0 <τ<1,anda,b≥0.It holds that

Lemma 2 ([20]):Leta,b, γ be positive real numbers,and τ ∈(0,1).Then,the following inequality holds:

III.MAIN RESULTS

A.Control Design

System(1) can be expressed in the matrix form

Then,we compute the parameters through the following algorithm.

It is noted that from Algorithm1 that the following inequality holds:

To make system(1) fixed-time stable,the control inputuis designed as

wherer1,r2are the dynamic parameters to be designed.It is worth pointing out that controller (10) is in a quasi-linear form which has a simple structure and is easy to implement,compared with existing control strategies using the back stepping design method.

B.Design of The Dynamic Parameters

Before designing the dynamic parameters,a set of new variables is introduced as below

It can be seen that the equilibrium isr1=1.Thus,we can deduce intor1(t)∈(0,1] fromr1(0)∈(0,1].When ∥z∥≤1,we have

which meansr1converges towards ∥z∥.Therefore,r1∈[0,1]always holds.

C.Stability Analysis

With the above controller and parameter dynamics given,we are ready to present the following theorem.

Theorem1:Consider system (1) under Assumption 1.If the controlleruis designed as (10) with the dynamic parametersr1,r2given by (12),in which the vectorK,matrixP,and constants α1, α2,β,τare determined by Algorithm1,then system 1) is globally fixed-time stable with a settling timeTfor any initial statex(0).Moreover,the settling timeTsatisfies

z=(z1,z2,...,zn)T z1zn

Proof:Consider the variable with to defined in (11).Then,we have

From(9),it can be obtained thatPmeets the following conditions:

V=zT Pz

Let .Then its derivative along with (17) can be computed as

The following proof is divided into four parts.Part I shows the fixed-time attractivity ofz,while the fixed-time convergence ofzis guaranteed in Part II.The fixed-time convergence ofxis derived from the dynamic ofzin Part III,and the upper bound of the settling timeTis estimated in Part IV.

Part I: Fixed-Time Attractivity of System(17)

In this part,we show that for any initial conditionz(0)∈Rn,z(t)will converge to a neighbourhood Ω={z|∥z∥2≤1} before a given timeT0.

Thus,at the time instantT,∥z(t)∥ andr1(t) converge to zero.

Part III: Fixed-Time Stability of System(1)

From the definition ofzin (11),it holds

Meanwhile,from (22),we have

The parameterr2can be estimated as

Therefore,following (33) and (37) yields:

z=(z1,z2,...,zn)T

Moreover,under the new variable,the control signalucan be expressed as

Asr1,r2andzare all bounded,thusuis bounded all the time.Moreover,from (34) we have l imt→T∥z(t)∥=0.

It can also be seen that

AsV(0) is determined by the initial state ∥x(0)∥ andr2(0) is chosen by the designer,we can conclude that the upper bounded of ∥x(t)∥ is governed by the initial system statex(0).

Part IV: Estimation of the Settling Time

which is not dependent on the system initial conditions.Therefore,the designed controller (10) and (12) can render system(1) globally fixed-time stable.

Remark 1:Our control strategy does not suffer from the singularity problem.It can be seen from (13) that ||z||,i.e.,||x||,converges to zero beforer1does.Therefore,even thoughr1tends to zero,the singularity problem for the control signaludoes not happen.Indeed,it is proved in Theorem1 that the control signal is always bounded and converges to zero in the end.

Remark 2:Our proposed control method is essentially different from the prescribed-time control methods in [9] and[11] in the following aspects: 1) Our considered system model is more general than the counterparts in [9] and [11].Specifically,the system model in [9] contains nonlinear dynamics that exist only in the last differential equation,while the system model in [11] has no nonlinear dynamics;2) The control action of our method does not have to terminate at the prespecified time instantTwhile the methods in [9] and [11]must.This is because [9] and [11] adopt a monotonically increasing function to achieve prescribed-time control.This function is only valid in the time interval [t0,t0+T),thus the control method becomes invalid whent≥t0+T.By contrast,our method does not need the above function and thus it keeps valid all the time.This property is particularly useful to cope with the case when the time instantTis not accurately determined.

IV.SIMULATION RESULTS

In this paper,we present two simulation examples to verify the effectiveness of our proposed method.

Example 1:Consider the one-link manipulator system given in [33]

Denotingx1=MDq,x2=andx3=Mτr,(40) can be transformed into

For simulation,the system parameters are set asD=5 kg·m2,N=0.2 ,M=0.5 H ,Km=0.05 N·m/A ,B=0.2 N·m·s/rad,andH=0.02 Ω.It can be verified that Assumption 1 is satisfied withc=0.04.Then,the control parameters are set ask1=2,k2=6,k3=3,τ=1/2,β=20.7, α1=0.2, α2=5,µ=3.In particular,according to Theorem1,the controller for this one-link manipulator system is designed as

wherer1,r2are the dynamic parameters designed as

The simulation results are presented in Fig.1.It is observed that the system statesx1,x2andx3converge to zero before the instantT=4 s.Meanwhile,the dynamic parameterr1remains in the interval [0,1] and converges to zero,whiler2increases to about 3 .4 and then remains the same.The control signaluis also bounded and converges to zero.Moreover,it can be seen that the closed-loop system can still operate beyond the time interval [0,4],which cannot be achieved through the pre-specified finite-time control method in [9] and [11].

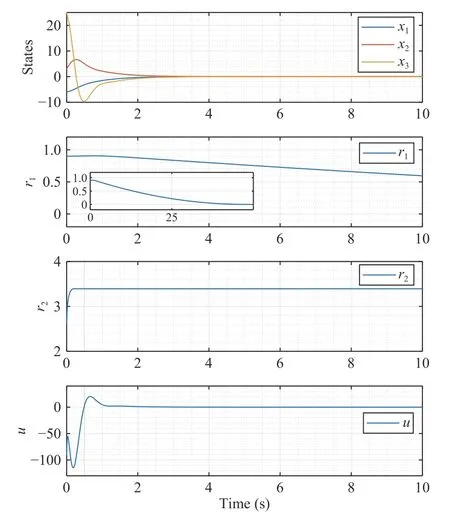
Fig.1.Simulation results for closed-loop system(41)−(43) with initial state x(0)=(−6,3,25)T.

Example 2:In this example,we consider a more complex robotic manipulator coupled to a DC motor to further confirm the effectiveness of our proposed method.The system model[34] is given as below

where the physical meanings of the relevant parameters are displayed in Table I.To facilitate the controller design,the following coordinate transformation is introduced:

TABLE I EXPLANATION OF PARAMETERS

Consequently,we have

For the sake of simulation,the system parameters are chosen asF1=F2=1 N·m·s/rad ,J1=J2=1 kg·m2,K=1 kgf/mm ,N=1,R=1 Ω ,L=1 H,Kb=1 V/rad/s ,Kt=1 N·m ,g=10 m/s2,m=0.5 kg,andd=0.2.The system’s initial condition is set asx(0)=[x1(0),x2(0),x3(0),x4(0),x5(0)]=[1,1,1,1,1,1],and [r1(0),r2(0)]=[1,1].

The control objective is to stabilize system(46).It can be verified that (46) satisfies Assumption 1,thus our control method can be applied.To show the effectiveness of our proposed method,we also compare our method with the one in[34].The control parameters of our method are set ask1=6,k2=k5=5,k3=8.5,k4=10,β=20.7,τ=0.5, α1=0.2, α2=5,and µ=3,while the parameters of [34] remain the same as those given in the simulation examples of [34].

The simulation results are presented in Fig.2.As can be observed,the system’s angular with our method converges to zero with a faster speed than the one in [34].Moreover,the amplitude of our control signal is also significantly smaller.This clearly demonstrates the advantage of our proposed method compared with the one in [34].

Fig.2.Simulation results.

V.CONCLUSION

This paper has proposed a dynamic gain control method to solve the fixed-time control problem for a class of strict-feedback nonlinear systems.The considered systems can describe a large class of practical systems with unmodelled dynamics satisfying a linear-grow th condition.To handle the unmodelled system dynamics,two auxiliary parameters are delicately designed.Our design method yields a quasi-linear controller which ensures that the closed-loop system is fixed-time stable.Compared with existing results,our proposed method avoids the “explosion of complexity”problem caused by conventional back stepping control.Moreover,the designed controller can keep operating beyond the given fixed-time instant without any control strategy switching,which is superior to the conventional prescribed-time control.Two simulation examples have verified the effectiveness of our proposed method.