Anti-Disturbance Control for Tethered Aircraft System With Deferred Output Constraints

Mengshi Song,Fan Zhang,,Bingxiao Huang,and Panfeng Huang, Senior

Abstract—In this paper,we investigate the peaking issue of extended state observers and the anti-disturbance control problem of tethered aircraft systems subject to the unstable flight of the main aircraft,airflow disturbances and deferred output constraints.Independent of exact initial values,a modified extended state observer is constructed from a shifting function such that not only the peaking issue inherently in the observer is circumvented completely but also the accurate estimation of the lumped disturbance is guaranteed.Meanwhile,to deal with deferred output constraints,an improved output constrained controller is employed by integrating the shifting function into the barrier Lyapunov function.Then,by combining the modified observer and the improved controller,an anti-disturbance control scheme is presented,which ensures that the outputs with any bounded initial conditions satisfy the constraints after a pre-specified finite time,and the tethered aircraft tracks the desired trajectory accurately.Finally,both a theoretical proof and simulation results verify the effectiveness of the proposed control scheme.

I.INTRODUCTION

THE relevant technology of the tethered aircraft system(TAS) is extensively applied in autonomous aerial refueling (AAR) systems [1],towed aerial recovery drogue systems[2],etc.It is known that the technological index of the position accuracy of the tethered aircraft is needed in practical applications,i.e.,the tethered aircraft is required to be constrained within a certain range and track the desired trajectory as accurately as possible.For example,in an AAR system,the drogue needs to stabilize itself in the neighborhood of the desired position to ensure the precise docking between the drogue and the receiver aircraft and avoid a collision with the receiver aircraft [3].

However,due to the unstable flight of the main aircraft and complex airflow disturbances [4],especially gusts,it is difficult to maintain the tethered aircraft within the expected range without the output constraint controller (OCC).Consequently,the OCC is vital for TAS.A necessary condition of the traditional OCC is that initial outputs satisfy constraints.Nevertheless,under airflow disturbances,the tethered aircraft may fluctuate greatly before the OCC operates,resulting in a situation where the tethered aircraft violates the output constraints at the beginning.In [5],the deferred output constraint is presented,which indicates the output constraint is imposed after the system runs for a period of time.By assuming that the output constraint is not imposed for a period of time after the system operates,the deferred output constraint also includes the situation where the output constraint may be violated initially.To sum things up,we can draw the conclusion that TAS satisfies the deferred output constraint rather than the traditional output constraint.

In recent decades,a lot of barrier Lyapunov function (BLF)-based control methods have been presented to cope with output/state constraints [6]–[8].In [9],a strict-feedback nonlinear system with output constraints is studied based on BLF.In[10],an adaptive control scheme is constructed for nonlinear stochastic systems with full state constraints by introducing symmetric and asymmetric BLFs.In [11],a BLF-based adaptive fault tolerant control method is presented to deal with the problem caused by state constraints and unknown faults of the elevators of hypersonic flight vehicles.It is known that these existing BLF-based control methods have a common prerequisite where the constraints are established from the beginning of the system operation.In other words,these methods cannot be directly used to solve the control problem of TAS subject to deferred output constraints.

To further deal with such problems,Song and Zhou [5] proposed a shifting function-based tracking control scheme of strict-feedback systems in the presence of deferred and asymmetric yet time-varying constraints.Although the method presented by Song and Zhou can not deal with the output constrained issue of TAS due to its nonlinear coupling characteristics,the shifting function in [5] has the ability to solve such problems.In the light of the shifting function,Sunet al.[12]developed the tracking control strategy of unmanned surface vessels subject to deferred asymmetric constraints.

From the control point of view,a key factor to enhance the tracking accuracy of the tethered aircraft is to improve the anti-disturbance ability of the controller by exactly estimating unknown disturbances.So far,many disturbance observers have been proposed to estimate disturbances accurately,such as the extended state observer (ESO) [13],sliding mode disturbance observer [14] and nonlinear disturbance observer[15].Among them,due to its high-performance and easy implementation [16],ESO is widely adopted in underwater vehicles [17],quadrotor unmanned aerial vehicles [18],AAR systems [19],etc.

The basic idea of ESO is to expand the unknown disturbance into a new state and then establish a novel extended state equation to estimate the new state in real time.An implicit condition of ESO is to avoid the large initial estimation error of the new state.Otherwise,the peaking phenomenon will appear due to the large observer parameters.Nevertheless,it is difficult to obtain exact initial values of observers in practice.

The peaking problem is an intrinsic characteristic of observers,which may lead to system performance degradation or hazards [20].Khalil and Praly [21] illustrated the basic principle of peak phenomenon in detail,and further analyzed it with simulations.Puet al.[22] designed an adaptive ESO with a linear time-varying form to inhibit the peaking phenomenon.Zhao and Guo [23] proposed a fal-based singleparameter-tuning ESO,resulting in better performance and smaller peaking value than the linear ESO.However,the existing ESOs only weaken the peaking value,and do not completely solve the peaking problem.Hence,an effective modified ESO to completely remove the peaking phenomenon is essential to improving system performance.

Inspired by the aforementioned analysis,to solve deferred output constraints and peaking problems,an anti-disturbance control method for TAS with the unstable flight of the main aircraft and airflow disturbances is proposed by introducing the shifting function into ESO and BLF.The main contributions of this paper are concluded as follows:

1) Unlike the previous works [24] and [25],the paper considers the fact that the main aircraft flies unsteadily,removing the common assumption that the main aircraft flies at a constant velocity.

2) Different from the current ESO [23],which can only weaken the peaking value,the modified shifting functionbased ESO (SFESO) completely circumvents the peaking phenomenon and guarantees the accurate estimation performance.

3) Compared with the existing BLF-based constrained control method [26] and [27],the improved output constrained controller solves the deferred output constraint problem of TAS by combining the shifting function and BLF.

4) By integrating the modified observer and improved output constrained controller into the dynamic surface control(DSC) scheme,an anti-disturbance control method is proposed,which ensures that the tethered aircraft with any bounded initial condition tracks the desired trajectory exactly and satisfies the output constraints after a pre-specified finite time.

The rest of this paper is organized as follows.In Section II,the tethered aircraft model and some technical lemmas are introduced.Section III constructs the SFESO and then designs the anti-disturbance control method for the TAS subject to deferred output constraints.In Section IV,the AAR system is simulated as an example to verify the effectiveness of the proposed control scheme.Finally,Section V concludes this paper.

II.PROBLEM STATEMENT AND PRELIMINARIES

A.Problem Statement

As shown in Fig.1,o g xgygzgis the inertial frame.To conveniently express the unstable flight of the main aircraft and establish the dynamic model of the tethered aircraft,oIxIyIzIis introduced as the reference frame,parallel toog xg yg zg,whereoIflies at a constant speedvI.l his the position vector fromoItoob,andlhand ξh,ϕhare the length and orientations ofl h,respectively.l iis the position vector from jointi+1 to jointiwithi=1,...,n.oh xh yh zh,o1x1y1z1andob xb yb zbare the body-fixed frame ofl h,l1and the tethered aircraft,respectively.ψ,ϑandγare the yaw angle,the pitch angle,and the roll angle of the tethered aircraft,respectively.For any vectorY,Y h,Y1andY bdenote the representation ofYinoh xhyhzh,o1x1y1z1ando b xb yb zb,respectively.

Fig.1.TAS configuration.

Remark 1:The lumped mass model is adopted to represent the tether,where each link is massless and elastic,and the natural length of each link is constant,except for the last link.The main purpose of the last variable link is to change the position of the tethered aircraft by controlling the release and recovery of the tether.The lumped mass model is widely used in the previous works involving TAS [28],which is not described in detail here.

The assumptions are given as follows.

Assumption 1:Because the attitude of the main aircraft has no effect on the tethered aircraft,the main aircraft is assumed as a particle located at jointn+1 to conveniently display the unstable flight of the main aircraft.

Assumption 2 [25]:Consider the situation that the reverse torque of the tether is large enough.The rolling angle of the tethered aircraft is very small,which is ignored here.

Assumption 3:Since the tethered aircraft is dragged by the main aircraft through a tether and flies at a high speed in the air,the tether is tensioned.

The translational dynamic model of the tethered aircraft inoh xhyhzhis formulated as

The attitude kinematic model of the tethered aircraft inob xbybzbis derived as

The attitude dynamic model of the tethered aircraft inob xb yb zbis given by

wherex dis the desired trajectory.

Further,define the deferred out constraints as

The control objective is to design an anti-disturbance controller for TAS (8) subject to the unstable flight of the main aircraft,airflow disturbances and deferred output constraints such that the tracking errorz1evolves within the specified constraint despite any bounded initial condition,and the deferred out constraints (10) are never violated after the prespecified finite timeTc.

Assumption 4 [2]:System statesx i(i=1,...,4) can be obtained directly or indirectly through the global positioning system(GPS),IMU,camera and tension sensor installed on the main aircraft and the IMU installed on the tethered aircraft.

Assumption 5:The inverse matrix ofexists.

B.Preliminaries

The shifting function is defined as [5]

whereTsis a pre-specified finite settling time.Nis a positive integer.

Lemma 1 [5]: s(t) has the following properties:

1)s(t) is strictly increasing for [0,Ts] withs(0)=0 ands(Ts)=1;

2)s(t)=1 fort≥Ts;

3) The time derivatives ofs(t) up to (N+1)th order are continuous and bounded.

Lemma 2 [29]:Considering the system=f(x L,u L) withx L∈Rnandu L∈Rmbeing the systemstate and input,if there exists a Lyapunov functionVL(x L) satisfying ς1(∥x L∥)≤VL(x L)≤ς2(∥x L∥) such that≤−σLVL(x L)+εL,in which ς1,ς2are classKfunctions,and σL,εLare positive constants.Then,the system statex Lis bounded.

Lemma 3 [30]:For |zb|<|kb| with ∀kb∈R+,∀zb∈R,the following inequality holds:

III.OBSERVER AND CONTROLLER DESIGN

In this section,the SFESO is constructed by combing the traditional ESO and shifting function,circumventing the inherent peaking problem in the observer.By using the shifting function to transform the output tracking errors,a SFESO based DSC scheme is developed,which ensures that the system outputs track the desired trajectories exactly and satisfy constraints after a pre-specified finite time,even if the initial outputs exceed constraint boundaries.

A.SFESO Design

Remark 6:Note thati=2,4 without special instructions in this subsection.In terms of the definition ofC3and Assumption 2,we know thatC3≈0,which does not need to be approximated by an observer but can be attenuated by the robustness of the controller itself.Therefore,onlyC2andC4are estimated by the SFESO designed in this subsection.

Assumption 6 [31]: C2,C4andare bou nded.

Because the shifting functions in the observer and controller do not affect each other,the setting time of the shifting function introduced in the SFESO can be different from that applied in the controller.Define the shifting function in the SFESO with the setting timeT oas

whereNo=1 satisfyingNo≥1 to ensure thatin (15) is continuous and smooth.

Define the auxiliary state as

Taking the time derivative ofx s,iand substituting (8) into it,one yields

Remark 9:About the constant vectorit is only introduced to guarantee the stability of the system at the initial stage,alleviating the negative influence of the excessive initial estimation error for the controller.Therefore,the exact initial value ofC iis not required.

Remark 10:The large observer gains in the observer with the initial estimation error always induce serious peaking issues,which may lead to further instability of the system[21].The result is not expected and needs to be avoided as much as possible in practice.In this SFESO,(0)=0,resulting in the situations where the initial estimation errors of (17) and (18) are completely removed.Therefore,by estimatingx s,i,instead ofx i,C i,the peaking issue is completely circumvented,even if the large observer gains are used in the SFESO.

B.Controller Design

To cope with the strong coupling nonlinear termA2in the system model (8),a modified coordinate transformation is introduced.Define the following tracking errors as:

where τiis the filtering output.

To solve the differential explosion problem about the virtual control signal,the following first order low pass filter is introduced as:

where λiis the positive diagonal matrix,and αiis the virtual control signal to be designed later.The filtering error is formulated as

Unlike the shifting function in the SFESO,the shifting functionsc(t) with the different setting timeTcis constructed as the following form in the controller:

Here,we adopt the above shifting functionsc(t) to obtain a novel transformation tracking error onz i,which is given by

Remark 11:In terms of Lemma 1,(27) and (28),the novel transformation tracking errorz s,1satisfiesz s,1(0)=0 andz s,1(t)=z1(t) fort≥Tc,regardless of the initial value ofz1.In the following steps,the property will be used to solve the deferred output constraint problem.

Step 1: According to (8),(23) and (28),the time derivative ofz s,1can be derived as

To address the deferred output constraint onz1,a barrier Lyapunov function aboutz s,1is expressed as

whereai(i=1,2,3) are the positive design parameters for the purpose of adjusting the magnitude of the followingk zssuch that its magnitude can be suitable for the virtual control law α1in (34).

The time derivative ofV1is denoted as

In terms of Young’s inequality,the following equations hold:

Then,the virtual control law α1is constructed as

Step 4: Similar to (37),the time derivative ofz4is described as the following form:

In the end,the anti-disturbance control law for TAS in the presence of the unstable flight of the main aircraft,airflow disturbances and deferred output constraints is designed as

wherek4is the positive diagonal matrix.

From(30),(38),(45) and (52),define the Lyapunov function as

On the basis of (35),(43),(50) and (55),the following inequality holds:

Based on the above analysis,the following theorem is presented.

Theorem 2:Consider the nonlinear system(8) under the unstable flight of the main aircraft,airflow disturbances and deferred output constraints.Suppose Assumptions 1–6 hold.By choosing the proper design parametersk i(i=1,...,4),λi(i=1,2,3) andb1satisfying the inequalities (58),the antidisturbance control law (54) is designed based on the SFESOs (13)−(21),the virtual control laws (34),(42),(49),and the first order low pass filter (24),which guarantees that 1)The tracking errorz1can be made arbitrarily small;2) The output constraint (10) is never violated after the pre-specified finite timeTc;3) A ll signals in the closed-loop system are bounded.

Proof:Integrating (57) yields

Considering (30),(56) and (59),the following inequality holds:

In terms ofz1=x1−x dand the boundness ofz1,x d,we can prove thatx1is bounded.Due to the definitions ofk zs,Q zs,it follows thatk zs,Q zsare bounded.Further,by using the fact thatare bounded,the boundness of α1is ensured.Sincee1=τ1− α1ande1is bounded,τ1is also bounded.Furthermore,based onz2=x2−τ1and the boundness ofz2,it is obvious thatx2is bounded.By continuing this reasoning process,the boundness of αi,τi(i=1,2,3) anduis proved.Therefore,all signals in the closed-loop system are bounded.

IV.SIMULATION RESULTS

This paper adopts the controllable drogue-based AAR system[25] as the simulation object,in which the tanker,hose and drogue are regarded as the main aircraft,tether and tethered aircraft,respectively.The physical parameters are selected as Table I based on [25] and [32].The acceleration ofthe main aircraft is chosen as[0.3cos(t),0.4cos(t),0.01cos(t)]Tdenoted ino IxIyIzIto show the unstable flight of the main aircraft.The design parameters are selected as

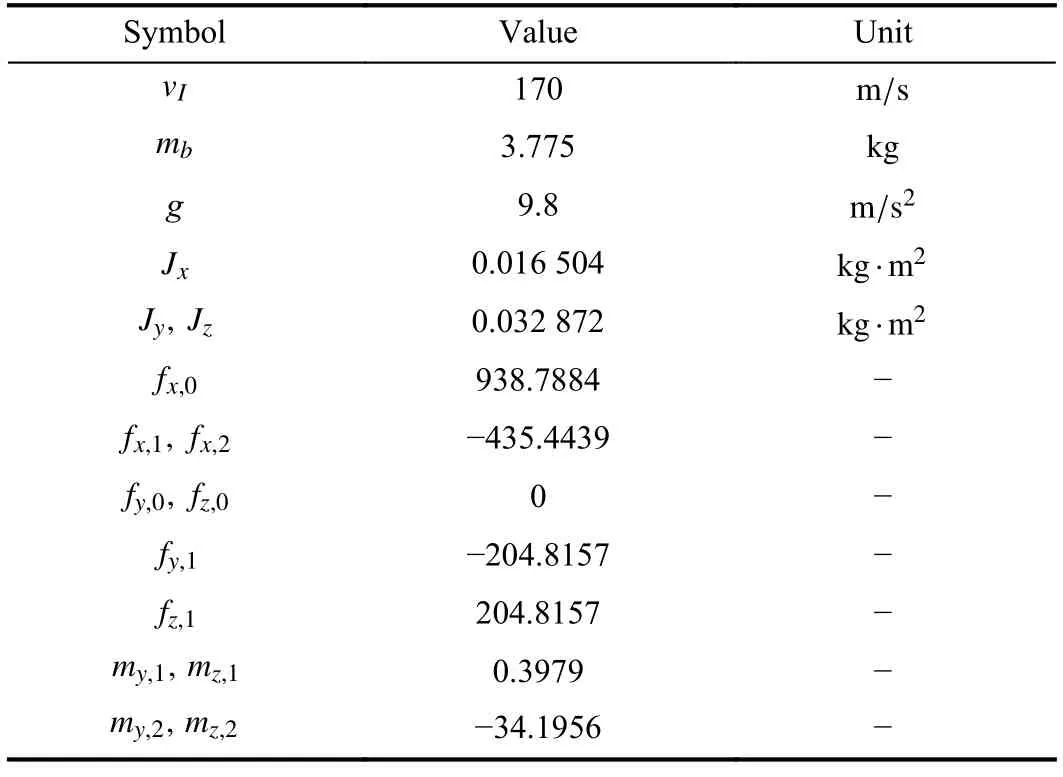
TABLE I PHYSICAL PARAMETERS

To verify the effectiveness of the proposed control method under different initial conditions,the following two cases are simulated,where the design parameters under the two cases are the same.

Case 1:Output constraints are violated at the beginning.The initialvalue of the tracking error isz1(0)=[0.0394,0.0013,0.0014]T.

Case 2:Initial outputs satisfy the constraints.The initial value of the tracking error isz1(0)=[0.01,0.0005,0.0008]T.

Fig.2 shows the composite airflow disturbances including the turbulence,gust and wake,in which the turbulence applies the Dryden turbulence model [25],the gust uses the cosine gust model,and the wake induced by the main aircraft adopts the Hallock-Burnham model [33].The figure proves that the airflow environment around TAS is complex and changeable,and that a gust is an extreme airflow disturbance,whose amplitude is much larger than that of the turbulence and wake within 6–12 s.The airflow disturbances bring great challenges to the accurate control of the tethered aircraft with deferred output constraints.

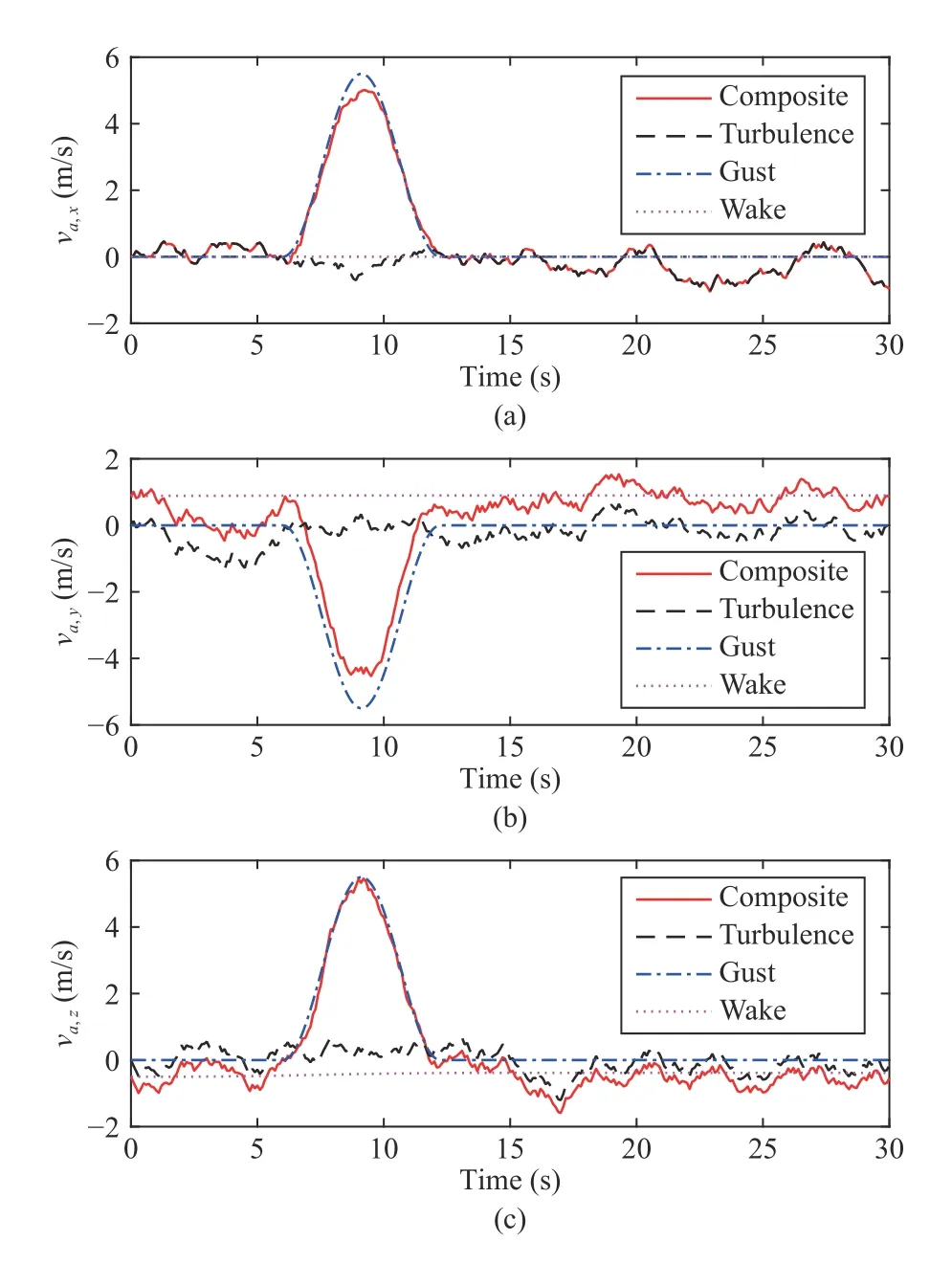
Fig.2.Composite airflow disturbances including the turbulence,gust and wake.(a) v a,x;(b) v a,y ;(c) v a,z.

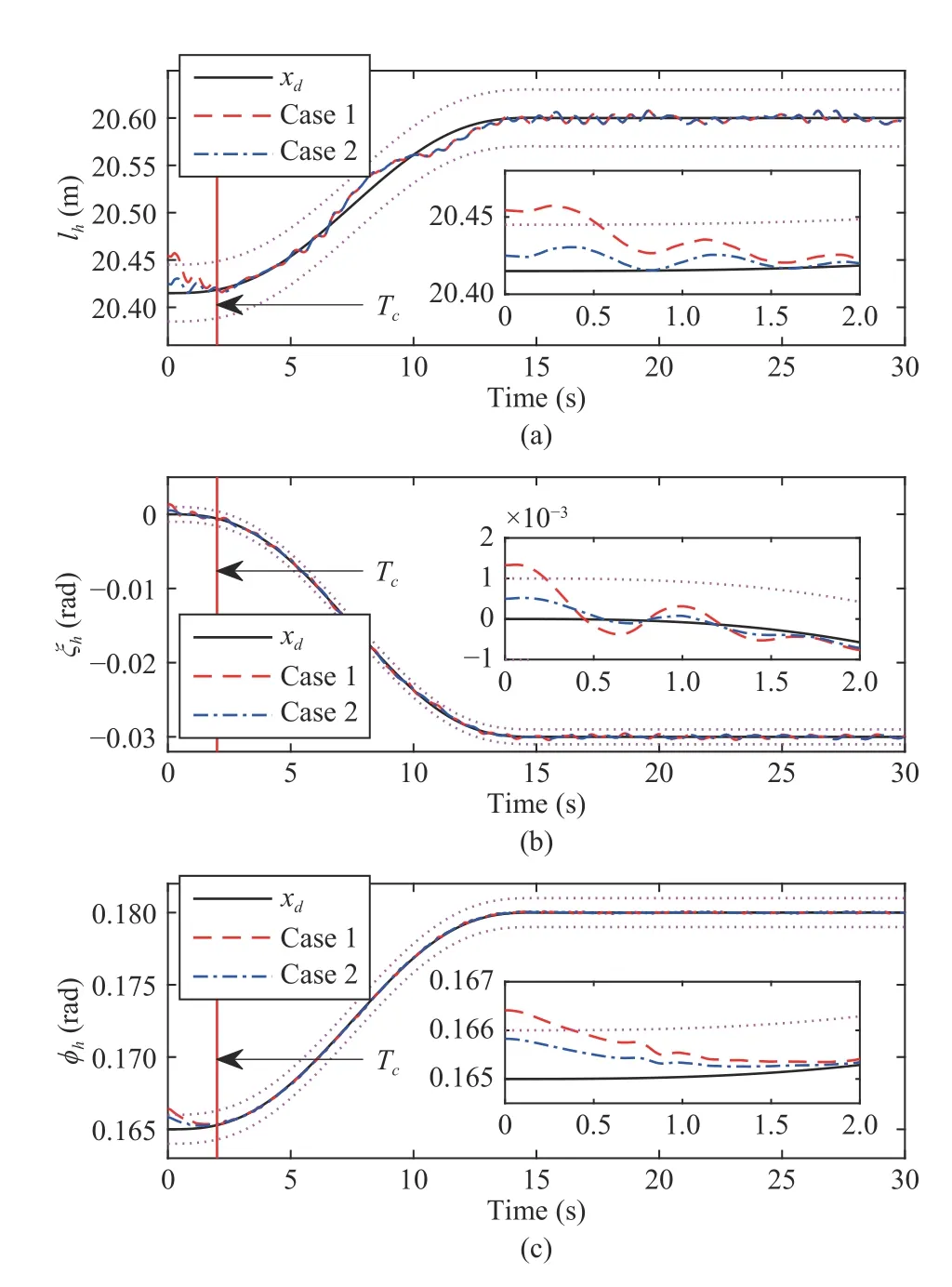
Fig.3.Tracking trajectories.(a) lh ;(b) ξh ;(c) ϕh.

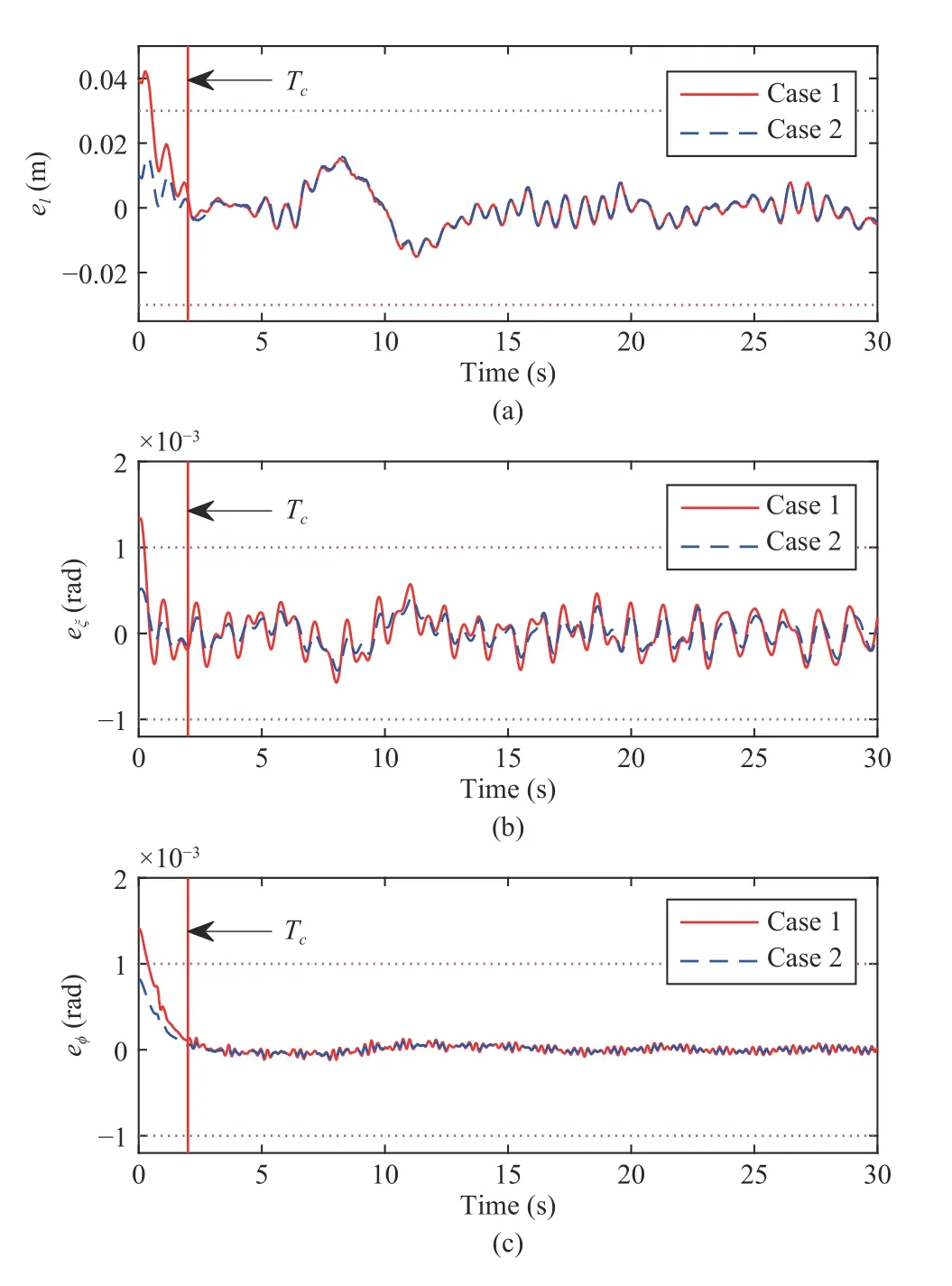
Fig.4.Tracking errors.(a) el ;(b) eξ ;(c) eϕ.

Figs.3 and 4 represent the tracking trajectories and tracking errors with the proposed control method in the presence of the unstable flight of the main aircraft,airflow disturbances and deferred output constraints under Cases 1 and 2,respectively.It is clearly observed that the tracking trajectories and tracking errors can meet the constraints after the pre-specified finite timeTc,whether the initial conditions violate or satisfy output constraints.Furthermore,in the face of complex and changeable airflow disturbances described in Fig.2,the tethered aircraft under the proposed control method can still accurately track the desired trajectory,except that the fluctuation ofelis slightly larger at 6–12 s in Fig.4(a) due to an extreme gust.

Fig.5 shows that the time response of the projection of the tether on thex-axis andy-axis in the presence of the unstable flight of the main aircraft at 15–30 s,where A0 denotes the barycenter of the tethered aircraft and A21 represents the jointn+1.It is obviously seen that the tethered aircraft is still stable in the case with unstable flight of the main aircraft.Fig.6 exhibits the time response ofls,which denotes the total length of the released tether.From Figs.5 and 6,we can draw the conclusion that the negative impact of the unstable flight of the main aircraft on the tethered aircraft can be eliminated by retracting and releasing the tether.

As depicted in Figs.7 and 8,the real values and estimations ofC′s,2andC′s,4with the proposed control method under Case 1 are exhibited,respectively,confirming good estimation performance of the SFESO.In addition,the peaking issue of the observer is completely circumvented because the initial values of the real values and estimations are equal to zero vectors by introducing (15).Further,it is clearly observed from Fig.8 thatC′s,4,xis not plotted because it is equal to zero during the whole process.Finally,the boundedness of the attitude angles and control inputs is also verified in Figs.9 and 10.

Fig.5.Time response of the projection of the tether on the x-axis and y-axis under Case 1.

Fig.6.Total length of the released tether under Case 1.

Fig.7.Time response of under Case 1.(a) ;(b) ;(c)

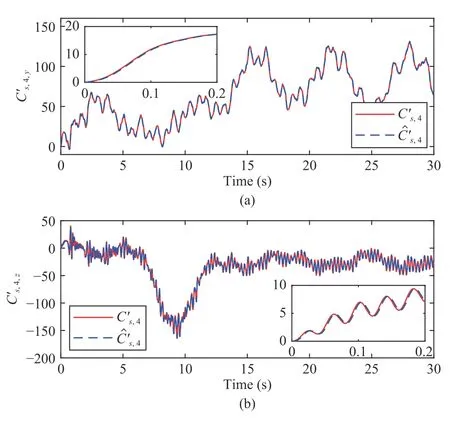
Fig.8.Time response of under Case 1.(a) ;(b)

Fig.9.Time response of ψ,ϑ, γ .(a) ψ ;(b) ϑ;(c) γ.

Fig.10.Control inputs.(a) tn ;(b) uz ;(c) uy.

V.CONCLUSIONS

This paper addresses the anti-disturbance control issue of TAS under the conditions of strong coupling nonlinearity,deferred output constraints,unmeasurable tether tension and tension torque,airflow disturbances,and unstable flight of the main aircraft.To deal with nonlinearity,the modified coordinate transformation is constructed.Then,the shifting function is introduced into the BLF-based DSC scheme to solve the deferred output constraint problem of TAS,even when the initial outputs violate constraints.Moreover,the lumped disturbances caused by unmeasurable tether tension and tension torque,airflow disturbances,and unstable flight of the main aircraft are estimated by the proposed SFESO,which also features the ability of completely removing the peaking phenomenon.Finally,the simulation results of the AAR system illustrate the effectiveness of the proposed control method for TAS.In the future,we will study the anti-disturbance control of TAS with deferred output constraints and input saturations,focusing on the trade off when they occur at the same time.

APPENDIX