A Novel Stackelberg-Game-Based Energy Storage Sharing Scheme Under Demand Charge

Bingyun Li,,Qinmin Yang,,and Innocent Kamwa,

Abstract—Demand response (DR) using shared energy storage systems (ESSs) is an appealing method to save electricity bills for users under demand charge and time-of-use (TOU) price.A novel Stackelberg-game-based ESS sharing scheme is proposed and analyzed in this study.In this scheme,the interactions between selfish users and an operator are characterized as a Stackelberg game.Operator holds a large-scale ESS that is shared among users in the form of energy transactions.It sells energy to users and sets the selling price first.It maximizes its profit through optimal pricing and ESS dispatching.Users purchase some energy from operator for the reduction of their demand charges after operator’s selling price is announced.This game-theoretic ESS sharing scheme is characterized and analyzed by formulating and solving a bi-level optimization model.The upper-level optimization maximizes operator’s profit and the lower-level optimization minimizes users’ costs.The bi-level model is transformed and linearized into a mixed-integer linear programming(MILP) model using the mathematical programming with equilibrium constraints (MPEC) method and model linearizing techniques.Case studies with actual data are carried out to explore the economic performances of the proposed ESS sharing scheme.

NOMENCLATURE

I.INTRODUCTION

DEMAND charge is an electricity rate scheme that is being widely applied to all kinds of electricity consumers [1].Monthly demand charge fee that is calculated based on the“billing demand”,i.e.,the maximumgrid-side power demand(kW) across all hours of the month,is added to a consumer’s electricity bill.Hence,electricity consumers tend to shave their peak power demands and save their bills by reshaping their load profiles,namely demand response (DR) [2]–[4].Effective and flexible DR operations are enabled by employing energy storage systems (ESSs),however,the high price and inefficiency of ESSs can deteriorate the benefits of ESSbased DR [5],[6].

ESS sharing is an effective solution to this issue.Alargescale ESS shared among a group of users can effectively promote their cost savings by taking advantage of the complementarity of the users’ load profiles as well as the economy of scale.The complementarity states that peak demands of different users may occur at different times of a day.Therefore,the shared ESS does not need to serve all users with complementary load profiles at the same hour.Thus,the requirement for ESS capacity is reduced.The economy of scale means that the unit price of ESS is lower when the purchased ESS is larger,i.e.,“the more,the cheaper”.

Lots of researchers have been studying on operating modes and performances of large-scale shared ESSs.Paridariet al.[7],Oh and Son [8],Liuet al.[5],[9]–[11],Yanget al.[12],and Li [13] proposed multiple ESS sharing schemes aiming at minimizing total cost of users,i.e.,maximizing social welfare.It is verified that ESS sharing can significantly reduce users’costs,compared to scenarios where no ESSs are deployed or users’ own ESSs are not shared.In addition to cost minimization,lots of researchers,such as Rahbaret al.[14],Taşcıkaraoğlu [15],Patnamand Pindoriya [16],and Taoet al.[17] involved various objectives such as photo voltaic accommodation,overload prevention,and multi-energy system objectives in their ESS sharing schemes.Thus,the benefits and operational flexibility of ESSs are promoted.However,these studies assume that all participants collaborate to maximize social welfare,regardless of their selfishness,which may make them impractical.Chenet al.[18] solved a multi-objective capacity dividing and scheduling problem of an ESS shared among users and a distribution company (DisCo).Balance between benefits of users and DisCo is achieved by properly setting weights of their objectives.Zaidiet al.[19] proposed an auction-based ESS sharing scheme.Users are assumed to compete with each other,instead of collaborating.Each user submits its bids for ESS capacity to the auctioneer.Fleischhackeret al.[20] assumed that the shared ESS is owned by an operator,and operator’s profit has priority over users’ cost savings.Benefits of both operator and users are verified via case studies.These schemes are more practical since participants’ selfishness is considered.

However,to the best of the authors’ know ledge,the demand charge scheme is always not incorporated in existing studies considering a large-scale shared ESS.Although some other literatures that targeted distributed and peer-to-peer energy sharing considered demand charge [21],[22],the majority of them either assumed cooperative participants or used faulty setup of demand charge.The demand charge scheme brings coupling effects to participants’ decisions across a month.Thus,it cannot be easily integrated into those existing ESS sharing schemes where only day-ahead decision-making is considered.How to integrate demand charge into an ESS sharing scheme considering participants’ selfishness remains an interesting problem.

The contributions of this paper are as follows:

1) A novel Stackelberg-game-based ESS sharing scheme is proposed for multiple electricity consumers under demand charge and time-of-use (TOU) price with participants’ selfishness considered.In this scheme,a large-scale ESS is owned and dispatched by a “leader”operator who sells electricity to“followers”users and sets its selling price.Users can purchase some electricity from operator instead of grid company to reduce their demand charges,in a practical scenario.All users and operator are selfish and apply their selfish operations.

Note that this scheme is different from hierarchical power sales in existing studies.Firstly,the considered market structures are different.Hierarchical power sales usually consists of a wholesale market and a retail market.Multiple competing retailers purchase energy from the wholesale market and sell it to end users.In the proposed scheme,the wholesale market is excluded;a new participant– the storage operator is involved.It purchases energy from the retail market and acts as a supplementary energy provider that helps users reduce their bills instead of a competing retailer.Secondly,our objective differs from those of the studies focusing on hierarchical power sales.Generally,the primary objectives of hierarchical power sales consist of maximizing each retailer’s profit[23]–[26] and emission reduction [27],[28],which take priority over user-side benefits such as in [25].In our study,the proposed energy storage sharing scheme is user-oriented.The guarantee of users’ benefits is primary.The storage operator’s profit can only be achieved after users’ further cost savings are guaranteed.Thirdly,in our study,the demand charge tariff is considered,which is rarely involved in existing studies focusing on hierarchical power sales.

2) Appropriate mathematical analyzing methods are applied to analyze the feasibility and economic performances of the proposed scheme.A bi-level operator profit maximization model is formulated and solved to characterize and analyze the economic performances of this Stackelberg-game-based ESS sharing scheme.The bi-level model is transformed into a mixed-integer linear programming (MILP) model using mathematical program with equilibrium constraints (MPEC) method and model linearization techniques.

The MILP model is solved using CPLEX.The economic performances,i.e.,users’ cost savings and operator’s profit,are demonstrated via case studies.Actual load data from the Pecan Street dataset [29] and TOU price from the Austin Energy company [30] are used in these case studies.

The rest of this paper is organized as follows.The ESS sharing scheme is introduced in detail in Section II.The bi-level optimization model for analyzing is founded in Section III.The model transformation and linearization procedures are given in Section IV.Multiple case studies are carried out in Section V.The potential for providing services to the grid using the shared ESS is discussed in Section VI.The paper is concluded in Section VII.The proofs of the existence and the nonuniqueness of the optimal solution are given in the Appendix.

II.MODEL OF THE ESS SHARING SCHEME

The setup of the proposed ESS sharing scheme is firstly given in Fig.1.Operator holds a large-scale ESS that is shared among users in the form of electricity transactions.User group contains residential users,small commercial users,and small industrial users.All users and operator are located in the same neighborhood and are connected to the same distribution transformer.It should be noted that operator is also charged by grid company according to the same electricity tariff that is applied to users,i.e.,TOU price and demand charge.

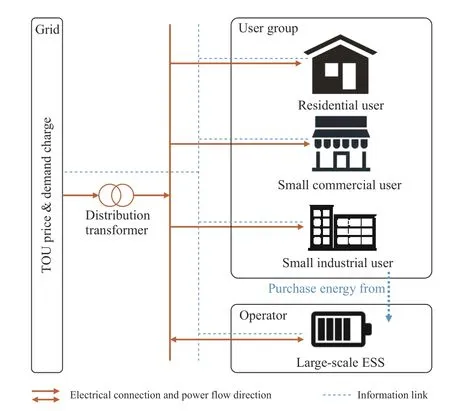
Fig.1.Architecture of the proposed ESS sharing scheme.

A.Interactions in the ESS Sharing Scheme

Advanced infrastructure enables bidirectional information exchanges among users,operator,and grid company,thus supporting their flexible interactions.The interactions among themare shown in Fig.2.

Fig.2.Interactions within the proposed ESS sharing scheme.

1) Users:Users are followers in the Stackelberg game.A user can choose to purchase any amount of electricity at any time from grid company or operator or both,as long as its own demand is fulfilled.Power flow #1 in Fig.2 is energy purchased by users from grid company.Cash flow #1 is users’corresponding electricity bills paid to grid company,which are calculated based on power flow #1 according to TOU price and demand charge.Power flow #2 is energy purchased by users from operator.Cash flow #2 is users’ corresponding electricity bills paid to operator,which are calculated based on power flow #2 according to the selling price set by operator.Power flows #1 and #2 fulfill users’ electricity demands.Cash flows #1 and #2 constitute users’ total costs.

2) Operator:Operator is the leader in the Stackelberg game.It sets the selling price of its electricity sold to users at the beginning of each month,and holds and operates a large-scale ESS to provide the energy sold to users.Power flow #2 and cash flow #2 in Fig.2 are users’ purchased energy and corresponding payments,respectively.Cash flow #2 is exactly operator’s income.After receiving a purchasing requirement and the corresponding payment from a user,operator has to deliver this user with its required amount of energy.It should be noted that the delivered electricity does not necessarily come from the discharging of the ESS (shown as power flow#5 →#2 in Fig.2).It is also allowed that operator purchases energy from grid company and directly delivers it to users(shown as power flow #3 →# 4 →#2 in Fig.2).Hence,charging and discharging operations of the ESS can be flexibly scheduled by operator.Besides,operator also purchases energy from grid company to charge its ESS,shown as power flow #3 →#6 in Fig.2.The electricity bill of operator is depicted as cash flow #3 in Fig.2,and is calculated based on its purchased power from grid company (shown as power flow#3 in Fig.2).This calculation is according to TOU price and demand charge schemes that are the same as those applied to users by grid company.

Essentially,both operator and users are regarded as electricity consumers by grid company since the same electricity tariff including TOU price and demand charge is enforced.From the perspective of an electricity consumer,operator’s load profile is exactly users’ summed purchasing demands that can be affected by operator’s selling price.The dispatching operations of the ESS are also operator’s DR actions.How to determine the selling price of operator’s electricity and manage the ESS to make this scheme profitable for both operator and users remains a challenge for further investigation.

B.Objectives of Users and Operator

1) Users:Each user aims to minimize its monthly electricity bill,i.e.,sum of fees paid to grid company and operator,by optimally deciding the amount of energy purchased from both sides at every hour across a month.

2) Operator:Operator intends to maximize its monthly profit,i.e.,revenue minus expense,by optimally setting its energy selling price and dispatching its ESS.Its revenue is exactly the income from selling energy to users.Its expense consists of its own electricity bill paid to grid company,and investments on its ESS.

Detailed model for analyzing the economic benefits of the proposed Stackelberg-game-based ESS sharing scheme will be given in Section III.

III.PROBLEM FORMULATION

The optimization model for characterizing the proposed ESS sharing scheme and analyzing its economic performances will be proposed in this Section.

A.Problem Overview

A bi-level optimization model is formulated to characterize the Stackelberg game between selfish operator and users,and to testify the economic performances,i.e.,operator’s profit and users’ savings,of the proposed scheme.

The upper-level problem in the bi-level model is the profit maximization problem of “leader”operator,since it sets its energy selling price and announces it to users before users send their purchasing operations.The lower-level problem is the cost-saving problem of every “follower”user.The interactions between the two levels are shown in Fig.3.The lower level problem will be introduced first since it is involved as a constraint in the upper-level problem.

Fig.3.Interactions between the two levels.

B.Lower-Level Model: User Cost Minimization

The lower-level problem is the cost minimization problem of each user.The objective function of useriis given as its monthly expense:

The constraints are given as (2)−(4) below:

A user is not allowed to purchase electricity more than its demand from operator:

A user is not allowed to sell energy back to operator:

The billing demand of useriis calculated as follows:

Therefore,for each useri,the lower-level problem can be modelled as the following linear programming (LP) model:

It can be seen that,for each hourt=1,2,...,T,there exist three constraints (2)−(4).Therefore,there are 3Tconstraints in total in (5).Such a large number of constraints will cast a shadow on the solving time of the bi-level problem,since a large number of integer decision variables will be involved by model linearization.This will be further explained in Remark 1 in Section IV.Therefore,the number of constraints in the lower-level model must be reduced.

A new model with far fewer constraints will be given in the rest of this subsection.First,the following assumption is given:

Assumption 1:The optimal energy selling price of operator is higher than the TOU price at any hour across a month,i.e.,ro>rg(t) holds for allt=1,2,...,T.

This assumption is reasonable since that if there exists a specifictwherero≤rg(t),users will purchase electricity as much as possible from operator.This will exhaust the operator’s ESS and result in a burdensome demand charge bill of operator.

Then,the following observation about the optimal solution of the lower-level model (5) is given:

C.Upper-Level Model: Operator’s Profit Maximization

The upper-level problem is the profit maximization problem(modelled as a cost minimization problem) of operator.The objective function to minimize is the net cost of operator:

The first two terms in (10) are investment costs of the ESS,including costs of inverter and battery,respectively.The third and fourth terms are operator’s energy fee and demand charge,respectively.The fifth termis the sum of fees paid by users for their purchased energy.

The constraints are modelled as (11)−(26) below:

Formulae (11)−(19) are constraints of the ESS.The energy conservation lawis:

The charging power and the discharging power cannot exceed inverter power capacity,respectively:

The charging power and the discharging power cannot exceed battery power limits,which are usually proportional to battery energy capacity,respectively:

The battery cannot be charged and discharged at the same time.Moreover,the battery is not allowed to be discharged when none of users send purchasing requests:

Battery state of charge (SOC) limits are enforced to prevent overcharging and overdischarging:

At the start and end of a month,the amounts of stored energy must be the same:

The following constraint calculates the billing demand of operator:

Formulae (21)−(23) are interaction constraints.Operator is not allowed to sell energy back to grid company:

It is observed that (17) is redundantly covered in (21).

The peak load at distribution transformer must not increase after adopting ESS sharing:

A constraint that guarantees users’ “further cost savings”should be involved to make this ESS sharing scheme attractive to them.This constraint states that each user’s total cost must be less than or equal to its total cost when it deploys an individual ESS without sharing:

However,guaranteeing all users’ “further cost savings”may severely hurt operator’s profit.Consider a user who consumes 10 kWh of electrical energy at 4:00 pm–5:00 pmevery day in July,and does not use any electricity at other hours.Such a user can achieve significant cost savings by optimally deploying and scheduling its own ESS.However,guaranteeing the“further cost savings”of this user will result in an unbearable low energy selling price of operator,since this user has to purchase at least 31xkWh of energy from operator to reduce its billing demand byxkW.

Hence,to avoid the harmful effects of such extreme user behaviors,it is allowed that a small part of users’ “further cost savings”are not guaranteed:

These users whose “further cost savings”cannot be guaranteed are denoted as “dropped”users.are binary variables indicating whether a user is “dropped”or not.kdropis the“drop rate”that is set as 0.1 in simulations.The value ofkdropis not a concern of this paper.

The lower-level problem is also a constraint here:

Here,the upper-level problem is formulated as:

It should be noted that (27) is also the bi-level optimization problem for characterizing the proposed ESS sharing scheme and analyzing its economic performances.

IV.TRANSFORMATION INTO MILP

In this section,the bi-level model (27) will be transformed into an MILP model.The problem is NP-hard and thus difficult to search for the global optimal solution.After the transformation,the solving time for the resulted MILP model can be effectively shortened using mature solving software where advanced pruning strategies are integrated.

The transformation process consists of two steps.In Step 1,the bi-level model (27) is transformed into an equivalent single-level optimization model using MPEC method [18],[31]–[33].In Step 2,since general MPECs are uneasy to solve,the single-level model is linearized into an MILP model which can be solved by mature algorithms.

A.Step 1: Transformation into MPEC Model

In this step,the bi-level model (27) will be transformed into a single-level MPEC model,by replacing the lower-level problem(26) with its Karush-Kuhn-Tucker (KKT) conditions.

The KKT conditions consist of primal constraints,dual constraints and complementary slackness conditions:

1) Primal Constraints:(7)−(9).

2) Dual Constraints:

where the Lagrange functionLis omitted for brevity.

3) Complementary Slackness Conditions:

By replacing (26) with its KKT conditions,the single-level MPEC model is given as:

B.Step 2: Linearization into MILP Model

In this step,the single-level MPEC model (48) will be linearized into an MILP model using multiple linearization techniques.

It is observed that the nonlinearities in (48) come from two sources: 1) the nonlinear constraints (16) and (31)−(33);2) the nonlinear termthat lies in the objective function(10) and the constraint (24).Two linearization techniques will be used to deal with these nonlinearities accordingly.

1) Linearizing (16) and (31)−(33):The big M method [34]is used here to linearize these constraints.DenoteMas a sufficiently large positive number andas new binary decision variables,the derived linear constraints are shown as follows:

Remark 2:It should be noted that using the big M method will involve one binary variable for every single constraint dealt with.Therefore,if the original model of the lower-level problem(5) is used instead of the simplified model (6)–(9),the number of binary variables will be extremely large,which can lead to an impractical solving time.

2) LinearizingThis nonlinear term can be eliminated by using the strong duality condition of the lower-level problem.The strong duality condition states that the optimal values of primal and dual objective functions are equal:

where the primal objective functionoiis given by (6) and the dual objective function is given as follows:

By substituting (6) and (44) into (43) and rearranging the terms,the following equation is derived:

It can be observed that the left-hand side of (45) is the considered nonlinear term,and the right-hand side of (45) is linear with respect to all the decision variables.By denoting Ξias the right-hand side of (45),the objective function (10) and the constraint (24) can be rewritten into the followings,respectively:

whereY mdenotes the decision variables,i.e.,Ysand the binary variables involved by the big M method.This MILP model can be solved using mature softwares.

V.CASE STUDIES

In this section,case studies will be carried out to demonstrate the economic performances,i.e.,users’ cost savings and operator’s profit,of the proposed ESS sharing scheme.

A.Real Data as Input

Actual data of users’ load profiles and electricity tariffs are used in the simulations.The load profiles of electricity consumers in Austin,TX,USA in July 2019 from the Pecan Street dataset [29] are used as users’ load data.Consequently,the electricity tariff of the Austin Energy Corporation [30] that serves electricity consumers in Austin is used.The TOU price is $0.08994/kWh at 4 p.m.–6 p.m.and $0.05261/kWh at other hours.The demand charge rate is $7.99/kW.Other parame-ters are shown in Table I.Note that the unit prices of the ESSCP,cap,CE,capare average monthly costs set the same as those in [11].

TABLE I PARAMETERS USED IN SIMULATIONS

fiare obtained by assuming users optimally decide the sizes and dispatching operations of their own individual ESSs.

B.Simulation Results

In this part,the MILP model (48) will be solved to demonstrate the economic performances of the proposed ESS sharing scheme.For comparison,a baseline case where no ESSs are used and a case where users deploy their own non-sharing ESSs are also simulated.It should be noted thatfiare exactly users’ optimal costs in the latter case.

Operator’s profit is calculated as $97.04.The sum of operator’s monthly average ESS investment costs and electricity bill is $67.13,and the revenue by selling electricity is$164.17.These results indicate that operator’s benefit is achieved.The optimal electricity selling price of operator is calculated as $1.5843/kWh,which is far higher than the TOU price of the grid company.Thus,Assumption 1 holds.

Fig.4 shows operator’s load profiles with and without ESS scheduling.Note that the original load curve is exactly the sum of users’ energy purchasing demands.It can be seen that,through optimal ESS scheduling,operator’s peak demand is effectively reduced,which achieves a far less demand charge fee and consequently a satisfactory profit.As discussed in Appendix-B,the solution of the shifted load curve is not unique.The ESS can be charged at any time as long as the operator’s peak load power is not increased.Moreover,it can be seen that the ESS is idle at lots of time slots.This indicates that the operator has the potential to welcome more users or provide some ancillary services to the grid.Both of these aspects of its potential will be discussed in the rest of this paper.

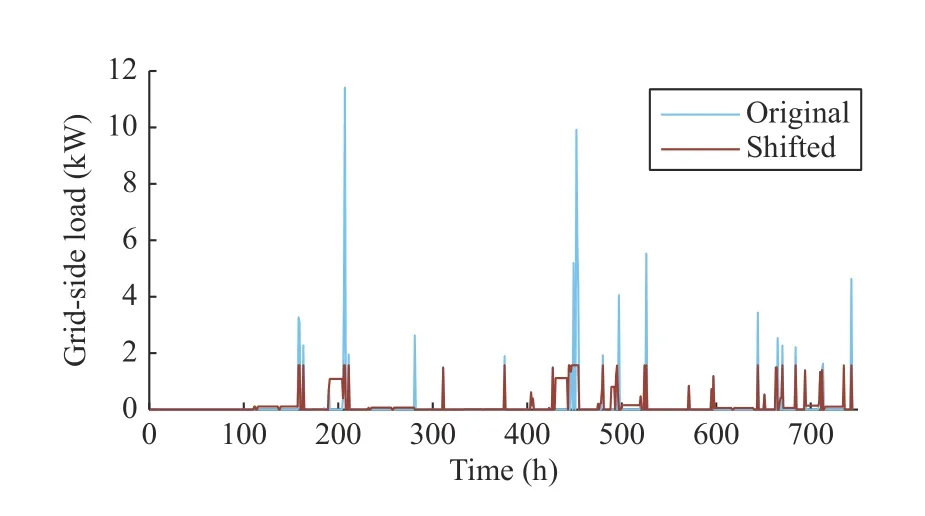
Fig.4.Operator’s original and shifted load profiles.

Fig.5 shows users’ cost savings compared to the baseline.It can be seen that all users can save some expenses using the shared ESS.Users 1–6,8,and 10 achieve “further cost savings”compared to the case where they deploy their non-sharing individual ESSs.Especially,the cost saving of User 2 triples after participating in the ESS sharing scheme.The cost saving of User 9 is equal to the value when it deploys its own non-sharing ESS.User 7 is the “dropped”user whose saving slightly decreases.Note that although User 7 is “dropped”in the studied month,it is not likely to be “dropped”in another month,since users’ load profiles vary across months,and the operator chooses the “dropped”user by optimization with all users’ load profiles considered.Even if there is indeed an unlucky user who is frequently “dropped”,its losses can still be compensated by subsidies.

All users choose to purchase electricity from operator in 5 hours across the month.Part of the original and shifted load profiles of User 2 and User 10 are shown in Figs.6 and 7,respectively.It can be seen that the peak demand of User 2 is quite protruding.By purchasing just a little electricity from the operator,this peak can be effectively shaved,and thus the demand charge fee of User 2 will be significantly lowered.Therefore,a cost saving of over 10% is observed in Fig.5.If User 2 decides to deploy its own ESS instead of participating in this sharing scheme,an inverter with a large power capacity will be required,which will raise the ESS cost and thus reduce the cost saving.On the contrary,lots of peaks with similar values exist in the load profile of User 10.If this user chooses to shave a lot of peaks,its purchased energy from the operator will be too much to achieve any savings in its total cost.On the contrary,if it chooses to shave only a few of those peaks,the reduction in its demand charge fee will be small.Thus,User 10 can save only about 1% of total cost due to the high price of electricity from operator.

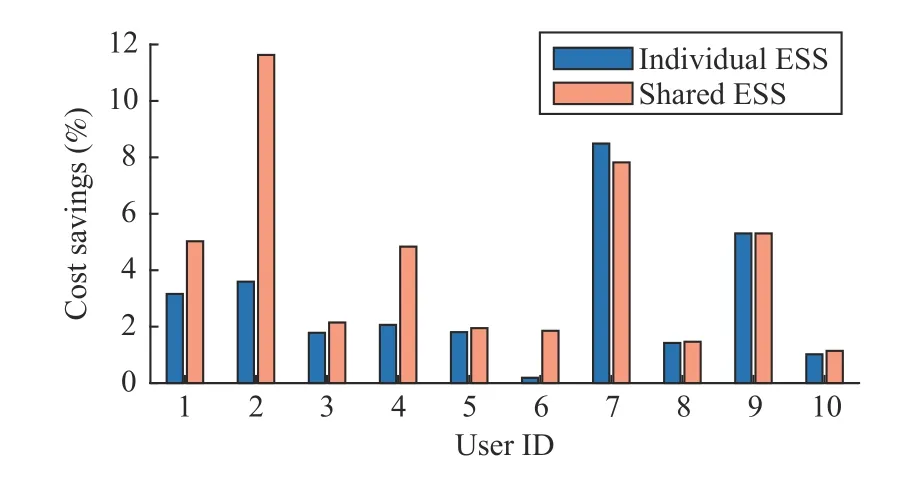
Fig.5.Cost savings of users compared to baseline.

Fig.6.Part of original and shifted load profiles of User 2.

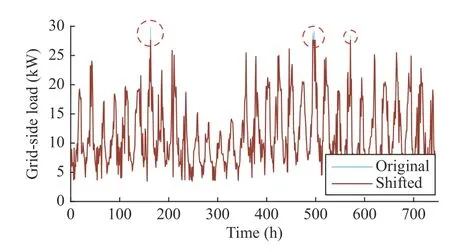
Fig.7.Original and shifted load profiles of User 10.Differences between two curves are marked by circles.

The solver is chosen as CPLEX 12.8 in MATLAB/Yalmip environment.The solving time is about 8 seconds by settingas 10.For comparison,the solving process is not terminated in half an hour whenis simply chosen as the set of all hours of the month.This indicates that a well-chosencan significantly reduce the solving time.

C.Analysis of Battery Ageing

In reality,the batteries of ESSs are affected by ageing effects.The actual capacity of a battery can decay to only 80%of the nominal value at the end of its lifespan.Therefore,a simulation withS OCmax=75% is carried out to explore the effects of battery ageing.The profit of operator is calculated as $90.14,which shows a slight decrease compared to the previous result of $97.04.The electricity selling price remains the same,indicating that users’ cost savings keep the same.The billing demand of operator is calculated as 2.45 kW,which is higher than the result of 1.57 kW in Fig.4.This is because that given a fixedkd,the maximum allowed discharging power of the battery falls with the decay of battery capacity.

D.Analysis of ESS Energy and Power Capacities

The energy capacity of the ESS batteryEcapand the power capacity of the ESS inverterPcaphighly impact the profit of operator.Simulations are carried out to clearly demonstrate the impacts.It should be noted that in these simulationsPcapis always set as 0.5Ecapfor simplicity,since the discharging rate of the battery is 0.5C.Fig.8 shows the results of operator’s profits under different values ofEcap.10 simulations with different load data are completed for eachEcap,and the average,maximum,and minimum values of operator’s profits are given.It can be seen that the operator can get profit in all the simulations.Ecap=20 kWh is the best choice in terms of the average or the maximum profit,whileEcap=25 kWh is the best considering the minimum profit.Operator’s profit decreases whenEcapis too small or too large.A smallEcapindicates that the ESS cannot store enough energy to fulfill users’ demands,and thus the operator has to purchase more energy from the grid,resulting in a higher demand charge fee.A largeEcapresults in expensive ESS investment costs.

Fig.8.Average,maximum,and minimum values of operator’s profit under different ESS capacities.

E.Analysis of Number of Users

According to previous discussions,a single user usually uses ESS sharing service for only about 10 hours per month.Therefore,it is expected that more users will lead to more discharging requirements which will make the ESS operate more frequently,and consequently more profitable for the operator.In this part,this guess will be verified via simulation studies by choosing 10 to 50 users.For each number of users,10 simulations with different users are carried out to get the averaged results.

Table II shows the operator’s average profit per user.It can be seen that with the grow th of the number of users,operator can indeed get more profit from each user.Moreover,the profit shows a large increment when the number of users grows from 10 to 20,and increases slow ly afterwards.This is because that users’ peak demand may overlap.If a new user’s discharging commands highly overlap with existing ones,theoperator will possibly have to deploy a larger ESS to fulfill them,leading to slower grow th of profit.

TABLE II OPERATOR’S PROFIT PER USER VS.NUMBER OF USERS

These results can demonstrate that the proposed ESS sharing scheme can benefit both users and operator.

VI.DISCUSSIONS ON PROVIDING GRID-SIDE SERVICES

In this section,the potential for providing services to the grid using the shared ESS facility will be explored.

As discussed before in Section IV-C,the charging profile of the ESS operator is flexible.Moreover,the discharging profile can also be flexible when providing services to the grid,as long as users’ energy purchasing demands are always fulfilled without increasing the operator’s peak load power.Therefore,by modifying the charging/discharging profile,some ancillary services can be provided to the power grid.Since reshaping the charging/discharging profile will directly result in changes in the aggregated load curve (i.e.,the summed load curve of all users and operator),the service of smoothing the aggregated load curve will be considered in this section.

A.The Optimization Problem

To smooth the aggregated load curve,the objective function is chosen as the sum of squared differences of aggregated grid-side load between two neighboring time slots:

The constraints include the following formulae:

Constraints related to the ESS: (11)−(15),(18),(19).

The demand charge fee of the operator must not increase after this grid-side service is provided.This means that the discharging power should not be less than the optimal value of problem(48),and the maximum charging power must not increase:

The battery cannot be charged and discharged at the same time:

Therefore,the optimization model is described as follows:

By linearizing (52) using the big M method,the model can be written as a convex mixed-integer quadratic programming(M IQP) model,which can be directly solved by CPLEX.

B.A Case Study

A case study based on the settings and results of Sections VA and V-B is carried out to demonstrate the load-smoothing performance of the shared ESS.

Fig.9 compares the optimized aggregated grid-side load profile of Days 21−24 and the original one derived from Section V-B.It can be seen that after this optimization,load peaks are obviously shaved,valleys are slightly filled,and frequent sharp rises and falls are smoothed.The optimized value of the objective function is about 67% of the original value,which can be interpreted as that the aggregated load curve is smoothed by about 33%.Fig.10 compares the charging and discharging power curves of the shared ESS.Firstly,charging and discharging operations are much more frequent after optimization,which shows the effort in smoothing load curve.Secondly,the maximum charging power is small due to the peak power limit (51),while the maximum discharging power is relatively large.This explains the observation that the load valleys are only slightly filled but the peaks are obviously shaved.

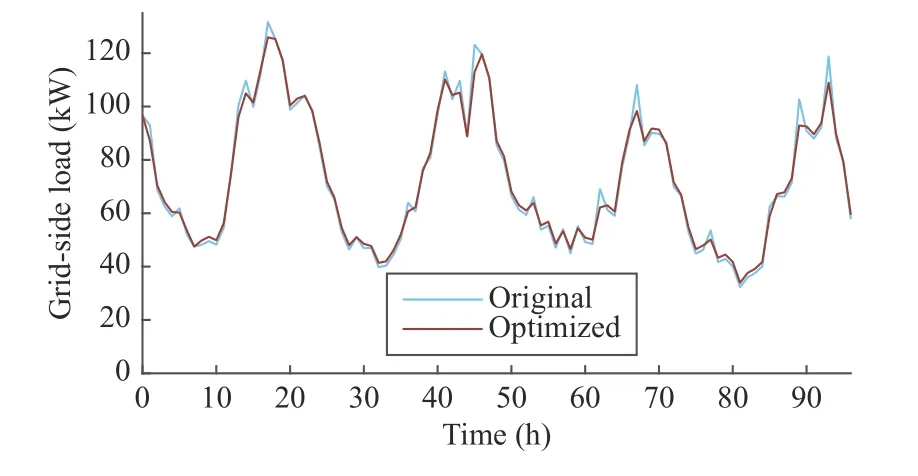
Fig.9.Comparison between optimized and original aggregated grid-side load profiles.

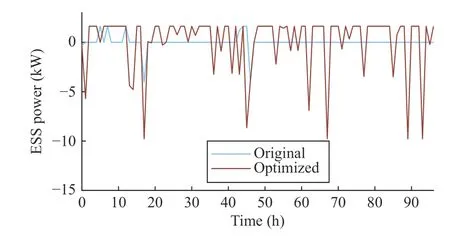
Fig.10.Comparison between optimized and original ESS power curves(positive means charging).

VII.CONCLUSION

In this paper,a novel operator-enabled Stackelberg-gamebased ESS sharing scheme is proposed for electricity consumers under TOU price and demand charge.Selfishness of both users and operator is considered in this scheme.Economic performances of the proposed scheme are analyzed by formulating and solving a bi-level operator-profit-maximizing optimization problem.Numerical results that are acquired by solving the model using real price and load data support the point that the proposed scheme can promote users’ cost savings and achieve operator’s profit.Moreover,this scheme also has the ability to provide some services for the grid.

The design of online day-ahead decision-making mechanisms of operator and users is a compelling extension of this study.How to incorporate load prediction uncertainties,especially the prediction uncertainty of future peak demands,remains a challenge.Recently,renewable energy such as wind energy [35]–[37] and photovoltaics [38] has become a research focus.How to cope with the uncertainties brought by users’ distributed renewable systems is also a concern.These will be studied in our next paper in the future.

In recent years,demand-side management in multi-energy systems is also an interesting research topic [39],[40].The involvement of heterogeneous energy carriers provides energy users a new degree of freedom for demand response,that is,conversion among different energy types.Therefore,energy sharing frameworks under multi-energy systems will be different and more flexible and thus are also listed in our future work plan.

APPENDIX

A.Proof of the Existence of the Optimal Solution

For continuous linear programming problems,a sufficient condition for the existence of the optimal solution is: The feasible set of the problem is a non-empty compact set,and the objective function is continuous on the feasible set.For mixed-integer linear programming with finite possibilities of integer values,it is trivial that a similar sufficient condition can be described as the combination of the following statements: 1) The feasible set is non-empty;2) Assume that the values of all the integer variables are fixed,then the resulted“continuous”subset of the feasible set is always compact;3)The objective function is continuous on all the non-empty subsets defined in 2).For the considered problem,we will prove that 1) and 2) hold;3) is trivial.

Proof of 2):We will show that when the values of integer decision variables are fixed,by adding some slack constraints that are always inactive,the resulted subset of the feasible set is always compact.It is trivial that the feasible set is closed since all the constraints are linear and all the inequality constraints are non-strict.Therefore,if a box set that covers the feasible set can be found,the feasible set is proved to be compact.

Firstly,we denoteCas a sufficiently large positive number and add some slack constraints:

Then,we will prove that these added constraints are always inactive.

Then,the required box set can be described as:

Therefore,the subsets are proved to be compact.

B.Proof of the Nonuniqueness of the Optimal Solution

However,it should be noted that,in all the optimal solutions,the values of the objective function are minimized and kept the same.Moreover,the interactions between the operator and users,i.e.,andro,are kept the same.The only difference lies in the operator’s charging/discharging profile,i.e.,Pc(t) andPd(t).