Adaptive Uniform Performance Control of Strict-Feedback Nonlinear Systems With Time-Varying Control Gain

Kai Zhao,,Changyun Wen,,Yongduan Song,,and Frank L.Lewis, Life

Abstract—In this paper,we present a novel adaptive performance control approach for strict-feedback nonparametric systems with unknown time-varying control coefficients,which mainly includes the following steps.Firstly,by introducing several key transformation functions and selecting the initial value of the time-varying scaling function,the symmetric prescribed performance with global and semi-global properties can be handled uniformly,without the need for control re-design.Secondly,to handle the problem of unknown time-varying control coefficient with an unknown sign,we propose an enhanced Nussbaum function (ENF) bearing some unique properties and characteristics,with which the complex stability analysis based on specific Nussbaum functions as commonly used is no longer required.Thirdly,by utilizing the core-function information technique,the nonparametric uncertainties in the system are gracefully handled so that no approximator is required.Furthermore,simulation results verify the effectiveness and benefits of the approach.

I.INTRODUCTION

IN practice,it is not difficult to design a proper control scheme such that all signals in the closed-loop systems are bounded in the presence of parametric/nonparametric uncertainties [1]−[4].However,the control problem becomes rather challenging if the sign of control coefficient is unknown.The first result was proposed in [5],where an adaptive control law using the so-called Nussbaum-type gain was designed.Motivated by such a technique,remarkable progresses were achieved by designing various adaptive control schemes so that the problem of unknown control direction with constant coefficient is solved ([6]−[8],to just name a few).

To deal with the case of unknown sign of control coefficient with time-varying yet unknown magnitude,a developed Nussbaum-based lemma was presented in [9].Its fundamental idea is to establish a Nussbaum function-based inequality such that the Lyapunov-like function is upper bounded by a Nussbaum function based manner.Due to the great success of such an approach,many results have been developed for handling unknown control directions with time-varying control coefficients [10]−[12].However,the stability proofs given in the above papers critically rely on some specific form of Nussbaum functions,which dramatically increases the complexity of stability analysis.To address such kind of issues,the work in [13] presented a general Nussbaum-gain-based lemma by developing some additional properties of Nussbaum functions and revealing its fundamental characteristics.This allows more types of Nussbaum functions to be employed to handle the problem of unknown control directions [14]−[17] and thus reduce the complexity of involved.Even so,it is still difficult to use such a lemma for strict-feedback nonlinear systems in the presence of unknown control directions.To our best know ledge,the main challenge is that there is no constructive guidance for us to design an adaptive law for Nussbaum functions so that it satisfies the precondition of the lemma in [13].Therefore,motivated by the above discussion,how to design an adaptive law for Nussbaum functions and then use this lemma to solve the control direction problem of strict-feedback nonlinear systems denotes an interesting issue.

Furthermore,tracking a known reference with pre-specified performance is of great importance in the practical applications [18].Up to now,some effective control methods on improving tracking performance have been proposed,see for example,prescribed performance bound (PPB)-based control[19] and funnel control (FC) [20].By introducing an error transformation,the PPB controls ensure that the error/system state converges to a pre-given set within a pre-specified convergence rate.However,the corresponding results are essentially semi-global since they require that the bound information on the initial condition of the system must be available for control design,otherwise it is impossible to ensure the desired performance specifications [11],[12],[21],[22].Fortunately,by constructing a class of performance funnels,the funnel control proposed in [20] was able to relax the limit on initial conditions of PPB control.Inspired by such an idea,there are some results developed for various kinds of nonlinear systems [23],[24].Recently,by constructing a global performance function,an adaptive back stepping control developed in [25] was able to ensure the asymptotic tracking with transient performance.However,it is difficult to extend the method in [25] to non-parametric systems with time-varying control coefficients.The main difficulties/challenges come from the following three aspects.The first is that the tuning function-based adaptive back stepping control cannot handle the problem of non-parametric uncertainty;The second challenge is the original lemma in [25] is invalid if the control gain is time-varying and unknown;The last but not the least is that the proposed method in [25] cannot unify the global and semi-global results without changing the control framework(see the detailed discussion in Remark 4).Thus,it is meaningful to develop new techniques to tackle the issue of uniform prescribed performance for non-parametric nonlinear systems with time-varying control coefficients.

In this paper,based on the parameter estimation technique,we aim to solve the uniform prescribed performance tracking problem for strict-feedback nonlinear systems with nonparametric uncertainties and unknown sign of control gain having time-varying magnitude.The main contributions of this article can be summarized as:

1) Different from the PPB-based controls [11],[12],[19],[21],[22],by constructing a unified function and a unique scaling function,the proposed control is flexible to handle the global or symmetric semi-global performance cases uniformly just by selecting the initial value of the time-varying scaling function properly,making the controller re-design and stability re-analysis not required;

2) Different from the specific form of Nussbaum functions in the existing literature [9]−[12],in this paper,by defining an enhanced Nussbaum function (ENF) and imposing a condition on the update law of Nussbaum argument,the developed control relaxes the complicated calculation and proof in the existing results;and

3) By extracting the core function information from the nonparametric uncertainty,no approximator (such as neural networks and fuzzy logic systems) is required,despite unknown control directions.

The remainder of the paper is organized as follows.Section II is the problem formulation.Some important functions for converting the required performance and the corresponding system trans formations are introduced in Sections III-A and III-B,respectively.Section III-D presents the control design as well as the stability analysis.Simulation studies are shown in Section IV to verify the theoretical result.The paper is concluded in Section V.

II.PROBLEM FORMULATION

In this paper,we consider the following nonparametric strict-feedback nonlinear system with arbitrarily given relative degreen:

wherexi∈R,i=1,...,n,is the system state withis the system output,and is a controly∈Ru∈R signal,represents an unknown parameter vector,denotes a smooth function,which contains the nonparametric uncertainty,gi(t)=biωi(t) is a time-varying control gain/coefficient,wherebi=1 or −1 represents the control directi on and ωi(t)>0:[0,∞)→R denotes the magnitude,both of which are unavailable for control design1R denotes the set of real numbers,R+is the set of positive real numbers,and R n represents the set of n−dimensional real vectors.Let |•| be the absolute value of a real number •..

Lete(t)=y(t)−yd(t)yd(t) be the tracking error with denoting the desired signal.The control objective of this paper is to develop an adaptive control algorithmfor (1) so that:

O1.All the closed-loop signals are bounded;and

O2.The uniform prescribed performance of tracking error can be ensured fort≥0.

Assumption 1:The desired signal and its derivatives up tonth are bounded,known,and piecewise continuous.

III.MAIN RESULTS

A.Performance Transformation

With respect to the second goal on prescribed tracking performance,we introduce the concept of unified function.

• Unified Function (UF).

Definition 1:A real composite function F(ϕ)∈R with ϕ ∈[−1,1]is called a unified function if it satisfies:

1)F(1)=∞,F (0)=0,and F (−1)=−∞;

2)F(ϕ)+F(−ϕ)=0;

3) F(ϕ):(−1,1)→(−∞,∞)is continuously differentiable with respect to (w.r.t.)ϕ;and

To ensure that the tracking error is within the pre-given region for ∀t≥0,we impose a unique time-varying scaling functionφto replaceϕin UF F,which has the following features:

●φ(k),k=0,1,...,is bounded,known,and piecewise continuous;and

●φ(t) with φ(0)=φ0is strictly monotonically decreasing w.r.t.time and limt→∞φ(t)=φfwith 0<φf<φ0≤1 being some constants,na mely,φ (t):[0,∞)→(φf,φ0][−1,1].

According to the definition of F and the properties ofφ,it is easy to get the conclusion that:

By utilizing the time-varying scaling functionφand the properties of UF F in Definition 1,the problem of prescribed tracking performance is stated mathematically equivalent to

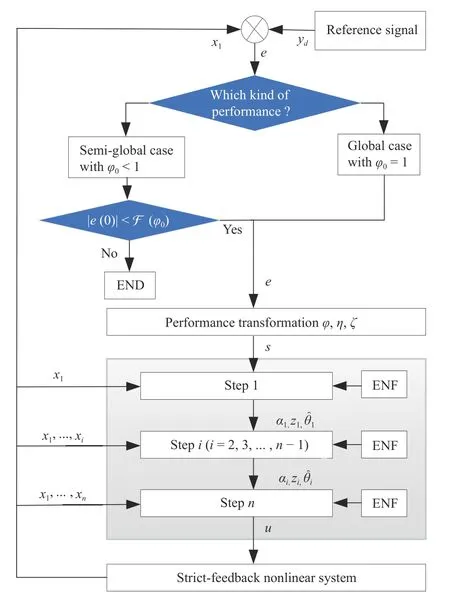
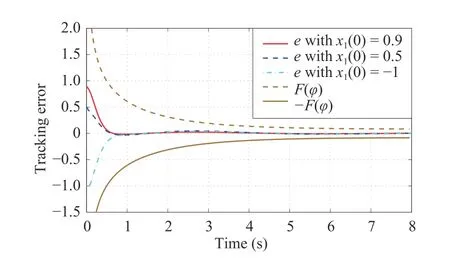
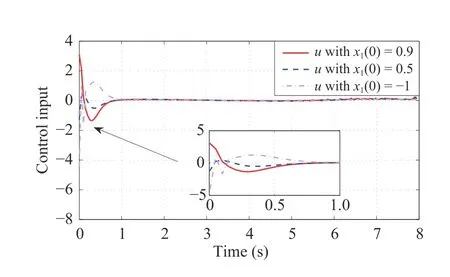
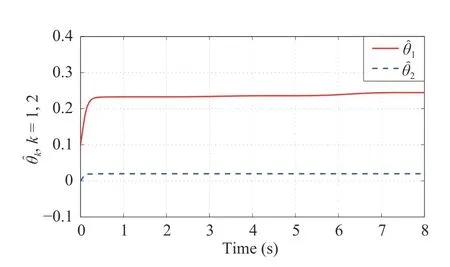
with the initial valuee(0)=e0satisfying F(−φ0)=−b0

Remark 1:It is worth mentioning that selecting different initial values of time-varying scaling functionφ,φ0,may lead to different results:

Case 1:If φ0=1,with the property of F in Definition 1,it follows that F(1)=b0=∞,which implies that the constraint on the initial error is vacuous,then the result is global;

Case 2:If φ0<1,it is seen that F(φ0)=b0<∞ withb0being a positive yet bounded constant,then the initial value has to satisfy |e(0)|

Therefore,the developed control without changing controller structure gives a unified framework to achieve the global and semi-global prescribed tracking performance uniformly by only choosing different value of φ0.

• Normalized Function (NF).

Actually,by noting that the form of (2) belongs to the error constraint problem,it is difficult and challenging to handle such an issue directly by utilizing the adaptive algorithm.In the following,we give a normalized functionηw.r.t.the tracking erroreto simplify the design difficulty of maintaining error constraint,i.e.,

which is equivalent to

It must be emphasized that,according to the properties of UF,it shows that:

Therefore,it follows from (4) that the performance given in(2) can be rewritten as:

Since F(·) is monotonic,the problem of unified prescribed performance in (2) (or (5)) can be further converted into

• Auxiliary Function (AF).

Let

be the so-called auxiliary function.As φ >0,(6) becomes

and the problem of prescribed performance in (2) (or (5) or(6)) is further converted into guaranteeing (8).

Let ζ0and η0be the initial values ofζandηatt=0,respectively.To achieve the prescribed tracking performance,the initial values ofeandηmust satisfy −b00.Furthermore,it is seen from (8) that this inequality actually belongs to the problem of constant yet symmetric constraint.Motivated by output/state/error-constrained control schemes [27],[28],if we are able to find a new variable such that the stabilization of the new variable is the sufficient condition of ensuring (8),then the constant and symmetric constraint is naturally achieved.Therefore,to this end,we give a definition of barrier function (BF) in what follows.

• Barrier Function (BF).

Definition 2:A real composite functions(ς) is a barrier function if it satisfies:

1) The initial value of ς is within the interval (−1,1);

2)s(ς):(−1,1)→(−∞,∞)is continuously differentiable w.r.t.ς;

3)s=±∞⇔ς →±1;

4)s=0⇔ς=0;

5)s∈L∞⇒|ς|<1;and

6) There exists a constant ρ>0 such thatover the interval Ω={ς ∈R||ς|<1} and ρ →±∞ if and only i ς →±1.

From the above discussion it is seen that the initial value ofζis within (−1,1).According to Definition 2,if we are able to utilize the composite functionsw.r.t.ζ(i.e.,s(ζ)) and to develop an advanced control method such thats(ζ)∈L∞for∀t≥0,together with the analysis in (2)–(8),the unified pref scribed tracking performance can be guaranteed.Thus we will focus on handling the stabilization problem of BFsin the remaining part of this paper.

B.System Transformation

Upon using the expression ofζas shown in (7),with the definitions ofηandφ,it is seen that

Therefore,it is obviously seen that if an adaptive control lawis designed such that the barrier functionsis bounded over [0,∞),then the objective O2on tracking performance is achieved.

C.Enhanced Nussbaum Function

For a smooth functionN(χ):R →R,denote its positive and negative truncated functions byN+(χ) andN−(χ),respectively,i.e.,

Obviously,the truncated functions satisfy the following properties:N+(χ)≥0 ,N−(χ)≥0 andN(χ)=N+(χ)−N−(χ).If a continuously differentiable functionN(χ) satisfies

then it is called a Nussbaum function,which has been widely employed for coping with the problem of unknown control directions.In this paper,to handle the unknown time-varying control coefficient with unknown sign and to reduce the difficulty of stability analysis,the concept ofenhanced Nussbaum function (ENF),inspired by [13],is presented.

Definition 3:A continuously differentiable functionN(χ) is called an ENF,if,for a constantL>1,it satisfies

According to the properties of Nussbaum function shown in(13) and (14),it is easy to check that the ENF also belongs to the Nussbaum function.To state the Nussbaum-based lemma later and to simplify the stability proof,we present the following lemma.

Remark 3:The problem of constant control gain with unknown control directions is solved in the existing works [6],[7],[8],[25],whereas the corresponding Nussbaum lemma is no longer applicable to the case in this work as the control coefficient is time-varying,which may affect the stability analysis.Moreover,although some efforts have been made to handle the problem of time-varying case [10],[11],[12],the stability proofs must critically rely on the explicit calculation for the particularly chosen Nussbaum functions.If other forms of Nussbaum functions are employed,the corresponding complicated stability must be re-proved and re-analyzed.In this paper,as long as the employed Nussbaum function and its argument satisfy Definition 3 and (18),for the case of time varying control coefficient,the onerous calculation process is not required,which reduces the difficulty of stability analysis.

D.Control Design

Here we present an ENF-based control for strict-feedback system(1) with unknown sign and magnitude of control coefficients.To this end,we utilize the coordinate transformation in what follows:

where is the virtual control law.

Before the control design,let αj−1

Note thatx2=z2+α1,then (27) can be arranged as

Since the nonlinear functionfidoes not satisfy the parametric composition condition,then the tuning-function based adaptive back stepping control [1] is no longer available.To solve this issue,we impose Assumption 3 in this paper for the nonparametric uncertainty so that we can obtain the deeprooted information,making the approximator not required.Therefore,we have

Hence,Ξ1can also be upper bounded by the following form:

where θ1is an unknown virtual constant as defined in (24),and

is an available function.

To handle the unknown sign of control gain with time-varying yet unknown magnitude,we employ the ENF to design the virtual control law α1,

By utilizing the characteristics of ENF,the following Nussbaum-gain technique based virtual control lawis given as:

Substituting the virtual control and adaptive law as defined in (52)–(54) into (55),we have

Solving the above inequality yields

where Πi=Vi(0)+θiδ.

Step n:The derivative ofznis

According to the developed control algorithm,we state the following theorem.

Theorem1:For the strict-feedback nonlinear system(1)with the time-varying control coefficients of an unknown sign.Under Assumptions 1−3,if the control law (60)−(62) is applied,the control objectives O1−O2are ensured.

Proof:Define the Lyapunov function candidate as

Substituting the true control law (60) and adaptive laws (61)and (62) into (64),it is deduced that

Fig.1.The designed procedure diagram.

Remark 4:The differences between our previous result [25]and this work are mainly exhibited in the system model and the control goal: 1) the non-parametric uncertainty (rather than the parametric uncertainty) in the system model;2) the time varying (rather than constant) control coefficient with unknown control direction;and 3) the uniform prescribed performance (rather than global performance).It is quite difficult and challenging for solving the above issues as the approach in [25] is invalid,for example,for the non-parametric uncertainty,the parameter decomposition condition in [25] does not hold so that the tuning-function-based control cannot be adopted;For the time-varying control coefficient,the Nussbaum lemma in [25] is still ineffective.To solve the above problems,different yet more advanced technical development must be adopted in this paper,we utilize the “core information”technique in Assumption 3 to handle the non-parametric uncertainty,reveal some additional properties of Nussbaum functions in Definition 3 and Lemma 2 to cope with the time varying control gain,and construct a unified function F(φ) in Definition 1 to solve the problem of uniform prescribed performance.Therefore,it is seen that,compared with [25],the proposed scheme has great contributions in control design.

Remark 5:To achieve the given objectives in this paper,two major difficulties are encountered,as discussed below.

1) The first is how to ensure the uniform performance for strict-feedback non-parametric systems,which cannot be solved with existing approaches.For example,the PPB control schemes [19],[22] for guaranteeing prescribed performance cannot be applied,because they always require a constraint on the initial error.In this paper,we construct a unified function F and a unique time-varying scaling function φ(t),by selecting different initial values of φ(t),the uniform prescribed performances can be handled.Furthermore,by employing the deep-rooted information,the nonparametric uncertainty in the system can be greatly handled without involving any approximator;and

2) The second is how to reduce the complex stability analysis caused by the problem of time-varying control gains with unknown control directions.For most of existing Nussbaumgain results [11],[12],[14],only a special Nussbaum function can be proved to be effective based on the explicit calculation on the particular function used.However,the associated stability proof of closed-loop systems is quite complex.In this paper,an ENF is proposed.By establishing some important properties (i.e.,(15) and (16)) and imposing some extra condition on the argument of Nussbaum function (i.e.,(18)),the developed Nussbaum-gain-based Lemma 2 does not rely on the explicit calculation for the particularly chosen Nussbaum functions.This facilitates the stability analysis with great convenience and flexibility.

IV.SIMULATION STUDIES

A.Validity Verification of the Proposed Control

To illustrate the effectiveness of the developed control algorithm,the following strict-feedback nonlinear system is considered:

Fig.2.The trajectories of tracking error with prescribed boundary under different initial values.

Fig.3.The trajectories of control input under different initial values.

Fig.4.The trajectories of parameters χ1 and χ2 under initial condition x(0)=[−1,0]T.

Fig.5.The trajectories of parameter estimates and under initial condition x(0)=[−1,0]T.

B.Comparison With the Existing Works

To verify the merits of the developed algorithmin Section III-D,we mainly give a comparison between the proposed control and the funnel control in [29].To make a fair comparison,we use the following one-link robotic system in[30] for simulation:

Now we give the detailed formulations of the funnel control in [29] and the proposed control in this paper.

Funnel control:

Proposed control:

where the design parameters and positive function are given asc1=3,c2=6, γ2=0.01,and ε(t)=exp(−0.4t).The initial values of parameter estimates are chosen as=0 and χ2(0)=−0.9.Under the funnel control (71) and the proposed control (72),the simulation results are shown in Figs.6 and 7.It is easily seen that the proposed control has better transient performances than these in the funnel control.

Fig.6.The trajectories of tracking error under the proposed control and the funnel control.

Fig.7.The trajectories of control signal under the proposed control and the funnel control.

V.CONCLUSIONS

An adaptive uniform prescribed performance control strategy has been developed for strict-feedback nonlinear systems with nonparametric uncertainties and unknown control directions.By utilizing some function transformations and developing some additional features of Nussbaum functions,together with the adaptive back stepping technique,the proposed control exhibits the following features: 1) the boundedness of all signals in the closed-loop systems is ensured;2) the uniform prescribed tracking performance can be ensured without changing the control structure;and 3) the complicated stability proof in the existing Nussbaum-based results is avoided.It is worth emphasizing that although the uniform performance can be ensured by utilizing the developed control,we only achieve the symmetric result,which sacrifices the overshoot of the tracking error in some degree.Moreover,only the single system is considered in this paper.Noting that network systems nowadays have received more and more attention due to its widely applications [31]–[33] (such as microgrids,distributed systems,and mobile robots),therefore,we will study the uniform prescribed performance problem of networked systems in the future work.