A Quantum Tanimoto Coefficient Fidelity for Entanglement Measurement

Yangyang Zhao,Fuyuan Xiao,,Masayoshi Aritsugi,,and Weiping Ding,

Abstract—Fidelity plays an important role in quantum information processing,which provides a basic scale for comparing two quantum states.At present,one of the most commonly used fidelities is Uhlmann-Jozsa (U-J) fidelity.However,U-J fidelity needs to calculate the square root of the matrix,which is not trivial in the case of large or infinite density matrices.Moreover,U-J fidelity is a measure of overlap,which has limitations in some cases and cannot reflect the similarity between quantum states well.Therefore,a novel quantum fidelity measure called quantum Tanimoto coefficient (QTC) fidelity is proposed in this paper.Unlike other existing fidelities,QTC fidelity not only considers the overlap between quantum states,but also takes into account the separation between quantum states for the first time,which leads to a better performance of measure.Specifically,we discuss the properties of the proposed QTC fidelity.QTC fidelity is compared with some existing fidelities through specific examples,which reflects the effectiveness and advantages of QTC fidelity.In addition,based on the QTC fidelity,three discrimination coeffi-cients are defined to measure the differ-ence between quantum states.It is proved that the discrimination coefficient is a true metric.Finally,we apply the proposed QTC fidelity-based discrimination coefficients to measure the entanglement of quantum states to show their practicability.

I.INTRODUCTION

IN recent years,quantum theory has received extensive attention and has been widely used in quantum computing[1]–[3],quantum cryptography [4],quantum game theory [5],pattern classification [6],[7],robust control [8],[9],quantum evidence theory [10],[11],and others [12]–[14].Moreover,due to the unique uncertainty principle of quantum mechanics,it is also used to deal with uncertain information as well as[15]–[17].Fidelity is the core concept of quantum information,which can measure the degree of similarity between quantum states [18],[19].In fact,fidelity is useful in many situations as a measure of the distance between quantum states.It is applied to quantum error correction [20],quantum communication [21],and measurement of quantum entanglement [22],[23].

Measuring the similarity between quantum states is actually measuring how close two density matrices are to each other in the appropriate Hilbert space.Therefore,unless further consideration is applied,the concept of similarity in any vector space is not a uniquely defined concept.It is well known that one of the most common fidelities is Uhlmann-Jozsa (U-J)fidelity [24],[25].However,U-J fidelity requires the calculation of the square root of the matrix,which is not trivial in the case of large or infinite density matrices.Since U-J fidelity is the maximumover purifications,U-J fidelity measured on a subspace is always greater than or equal to the true relevant fidelity for two pure states,which may introduce a bias in estimating the fidelity [26].In addition,U-J fidelity only considers the similar parts between quantum states,namely that it is a measure of overlap.In this context,U-J fidelity may have counter-intuitive results under certain cases.

Considering the above issues,fidelity has received a lot of attention,and many alternatives of U-J fidelity have been proposed.For example,Chenet al.[27] proposed an alternative fidelity measure with a hyperbolic geometric interpretation.According to Chenet al.’s fidelity,Mendonçaet al.[28] proposed a fidelity measure called super-fidelity,which provides the upper bound of U-J fidelity.The super-fidelity does not need to calculate the square root of the matrix;but for orthogonal quantum states,a non-zero value is obtained.Correspondingly,Maet al.[29] proposed quantum affinity as a fidelity measure,called A-fidelity,which provides a lower bound of U-J fidelity.Wanget al.[30] proposed an alternative fidelity in terms of the Hilbert-Schmidt inner product between quantum states and their purity.However,it was found that Wanget al.’s fidelity may lead to unreasonable results in high dimensions.Recently,Ektesabiet al.[31] proposed a new alternative fidelity according to super-fidelity and Wanget al.’s fidelity.Nevertheless,Ektesabiet al.’s fidelity,like U-J fidelity,may show limitations in some cases.Therefore,the research on fidelity is still an open issue.

In this paper,a novel quantum Tanimoto coefficient (QTC)fidelity is proposed.The QTC fidelity only requires computing the Hilbert-Schmidt inner product between the given quantum states without computing the square root of the matrix.Therefore,the calculation of QTC fidelity is simpler than that of U-J fidelity.More importantly,the QTC fidelity not only considers the overlap between quantum states,but also takes into account the separation between quantum states for the first time,so it can better measure the similarity.Through some numerical examples,QTC fidelity is compared with several existing fidelities,which reflects the effectiveness and advantages of QTC fidelity.It is found that the QTC fidelity can distinguish superposition state and mixed state,which is not available in U-J fidelity.In addition,based on the QTC fidelity,three discrimination coefficientsandare defined to measure the difference between quantum states,and it is proved that theis a true metric.Finally,we successfully apply the proposed QTC fidelity-based discrimination coefficients to measure the entanglement of quantum states to show their practicability.

The contributions of this paper are summarized as follows:

1) The fidelity based on Tanimoto coefficient is proposed,which is called QTC fidelity.The QTC fidelity not only considers the overlap between quantum states,but also takes into account the separation between quantum states for the first time,which can better measure the similarity between quantum states.

2) Three discrimination coefficients based on QTC fidelity are proposed,which can measure the difference between quantum states,and it is proved that one of them is a true metric.

3) The proposed QTC fidelity-based discrimination coefficients are applied to measure entanglement between quantum states to verify their effectiveness and practicability.

The remainder details of this paper are organized as follows.In Section II,the definition and properties of U-J fidelity,some existing fidelities,and Tanimoto measurement are introduced.In Section III,the motivation,the definition and several properties of the novel fidelity are proposed.In Section IV,several examples are given to show the effectiveness of the proposed QTC fidelity.In Section V,some coefficients are defined based on the QTC fidelity to measure the difference between quantum states,and it is proved that one of them is a true metric.In Section VI,the proposed coefficients are applied to measure the entanglement of quantum states.Finally,the conclusion is given in Section VII.

II.PRELIMINARIES

In this section,we introduce the definition of U-J fidelity and its alternative fidelities,and classical Tanimoto measurement in information theory.

A.Uhlmann-Jozsa Fidelity

1) The Definition and Properties of Uhlmann-Jozsa Fidelity:Fidelity is an important concept in the field of quantum optics and information science.It provides a mathematical formula to quantify the similarity of a pair of quantum states.

When the concept of fidelity was first proposed [32],it was not applicable to arbitrary pairs of density matrices.However,it is implicit in this definition that for a pair of pure states ρ=|ϕ〉〈ϕ|a nd σ=|φ〉〈φ|,their fidelity is defined by the transition probability between the two states [32]

Equation (1) corresponds to the closeness of states in the natural geometry of Hilbert space,which generalizes readily to the case where one of the states is impure [32]

To obtain the fidelity of any two quantum mixed states,it may seemthat the following (3) serves as a useful generalization of (2) to an arbitrary pair of mixed states:

However,the Hilbert-Schmidt inner product leads to an unsatisfactory generalization of fidelity.For example,Idis the identity matrix acting ond-dimensional Hilbert space.For quantum states ρ=Id/dand σ=|ϕ〉〈ϕ|,thentr(ρρ)=tr(ρσ),so (3) is unsatisfactory as a measure of fidelity [24].

According to the “transition probability”of mixed states in[25],Jozsa [24] first defined the fidelity between two generic quantum statesρandσ,that is,the so-called Uhlmann-Jozsa(U-J) fidelity [24]

where |ϕ〉 and |φ〉 are restricted to be purifications ofρandσ,whileindicates that the maximization procedure can be explicitly evaluated.The value ofFUJ(ρ,σ) represents the similarity between the two quantum states,which is bounded in [0,1].The larger the value ofFUJ(ρ,σ),the more similar the two quantum states are.AndFUJ(ρ,σ)=1,if and only if it is applied to two identical states.

In [24],Jozsa conjectured that (4) was the only expression that satisfies some natural properties expected for any generalized fidelity concept.It is known as Jozsa’s axioms [24]:

a-1)FUJ(ρ,σ)∈[0,1],FUJ(ρ,σ)=1,if and only if ρ=σ;

a-2)FUJ(ρ,σ)=0,if and only if ρσ=0;

b)FUJ(ρ,σ)=FUJ(σ,ρ);|φ〉

c) Fidelity between arbitrary quantum stateρand pure state

d) Invariance under any unitary transformationUof the state space

In addition to the above Jozsa’s axioms,U-J fidelity has several less immediate properties.

e) Concavity: Forp1,p2≥0 ,p1+p2=1,and arbitrary density matrices ρ1,ρ2,andσ,U-J fidelity satisfies [24],[25]:

f) Multiplicativity under tensor products: For any density matrices ρ1,ρ2,σ1and σ2[24]:

An interesting consequence of (8) is that for two physical systems,described byρandσ,a measure of their degree of similarity given byFUJremains unchanged even after appending each of them with an uncorrelated ancillary stateτ,i.e.,FUJ(ρ⊗τ,σ⊗τ)=FUJ(ρ,σ).

2) The Limitations of Uhlmann-Jozsa Fidelity:Although UJ fidelity has been widely used,and this definition has many ideal properties,there are some limitations with U-J fidelity[26]:

a) U-J fidelity needs to calculate the square root of the matrix,which is difficult in the case of large or infinite density matrix.

b) Since the U-J fidelity is the maximum over purifications,the U-J fidelity measured on a subspace is always greater than or equal to the true relevant fidelity for two pure states,which may introduce a bias in estimating the fidelity of pure states.

Considering the above limitations,fidelity has received a lot of attention,and many alternatives of U-J fidelity have been proposed [26].

B.The Alternative Fidelity Measures

Chenet al.[27] proposed an alternative fidelity measure with a hyperbolic geometric interpretation [27]:

wherer=1/(d−1),dis the dimension of the state space,and

FNitself was proposed as an alternative to fidelity and is called super-fidelity,which defines the upper bound of U-J fidelity [28].Obviously,one advantage of super-fidelityFNis that it is easy to calculate.However,for mutually orthogonal matrices,(10) obtains a non-zero value.

In 2008,quantum affinity was proposed as a fidelity measure,called A-fidelity,which defines the lower bound of U-J fidelity,and needs to calculate the square root of the matrices[29]

Wanget al.[30] proposed an alternative definition of quantum fidelity for two density operators on qudits in terms of the Hilbert-Schmidt inner product between them and their purity[30]

Since Wanget al.’s fidelityFWdoes not satisfy (5),Ektesabiet al.[31] proposed a novel fidelity recently,which satisfies Jozsa’s four axioms,and was used to give an improved bound for quantum -speed-limit time in open quantum systems [31]

C.Tanimoto Measurement

The handling of uncertain information has received extensive attention,and many theories have been developed [33],[34].Tanimoto measurement [35],which is orthogonal to[36]–[39] is an effective tool to measure similarity.It is widely used in many fields,such as data fusion [40],and molecule structure similarity [41].The specific definition of Tanimoto measurement is as follows.

Definition 1:LetP={p1,p2,...,pn} andQ={q1,q2,...,qn}be two probability distributions.The Tanimoto measurement betweenPandQis defined as [35]

III.THE QUANTUM TANIMOTO COEFFICIENT FIDELITY

In this section,we first introduce the motivation of the QTC fidelity,then present the definition of the proposed QTC fidelity.Moreover,we discuss and analyze the properties of QTC fidelity.

A.Motivation of the QTC Fidelity

As we discussed in the previous section,U-J fidelity is the most widely used fidelity,but it needs to calculate the square root of the matrix,which is difficult in the case of large or infinite density matrix.Besides,in some cases,it cannot well reflect the similarity between quantum states.In accordance with the related alternative fidelity measures of U-J fidelity,they all have certain limitations in some cases.For mutually orthogonal matrices,super-fidelityFNobtains a non-zero value.A-fidelityFAneeds to calculate the square root of the matrices.Wanget al.’s fidelityFWmay lead to unreasonable results in high dimensions.Ektesabiet al.’s fidelityFE,like U-J fidelity,may show limitations in some cases.

The following Example 1 shows that U-J fidelity and Afidelity produce counter-intuitive results.

Example 1:Given three quantum states ρ1,ρ2and ρ3,satisfy the following equations:

xin ρ3changes from 0 to 0.4.To compare the similarity between quantum states in Example 1,we calculate the U-J fidelity and its alternative fidelities between ρ1and ρ2,ρ2and ρ3,and get the results as shown in Fig.1.It is worth noting that bothFUJandFAneed to calculate the square root of the density matrices,which is difficult for large or infinite density matrices,whileFN,FW,andFEdo not need to calculate the square root of the density matrices.From the results,we can see thatFUJandFAget the same result,but have different results from other alternative fidelities.The results ofFN,FWandFEshow that,regardless of the value ofx,the fidelity value between ρ2and ρ3is always bigger than that between ρ1and ρ2,that is,ρ3is more similar to ρ2than ρ1.However,the results ofFUJandFAshow that only within a certain range,ρ3is more similar to ρ2than ρ1.

Fig.1.The results of fidelity between quantum states in Example 1.

In fact,FUJandFAproduce counter-intuitive results.For example,whenxin ρ3is set to 0,ρ3=0.4|01〉〈01|+0.6|10〉〈10|.Whenx=0 ,FUJ(ρ1,ρ2)=0.8694,andFUJ(ρ2,ρ3)=0.7994,Fig.1(a) shows that ρ1is more similar to ρ2than ρ3.WhileFN,FW,andFEindicate that ρ3is more similar to ρ2than ρ1.

To visually compare whether the quantum state ρ2is more similar to ρ1or ρ3whenx=0,we visualize the quantum states ρ1,ρ2,and ρ3,as shown in Fig.2.

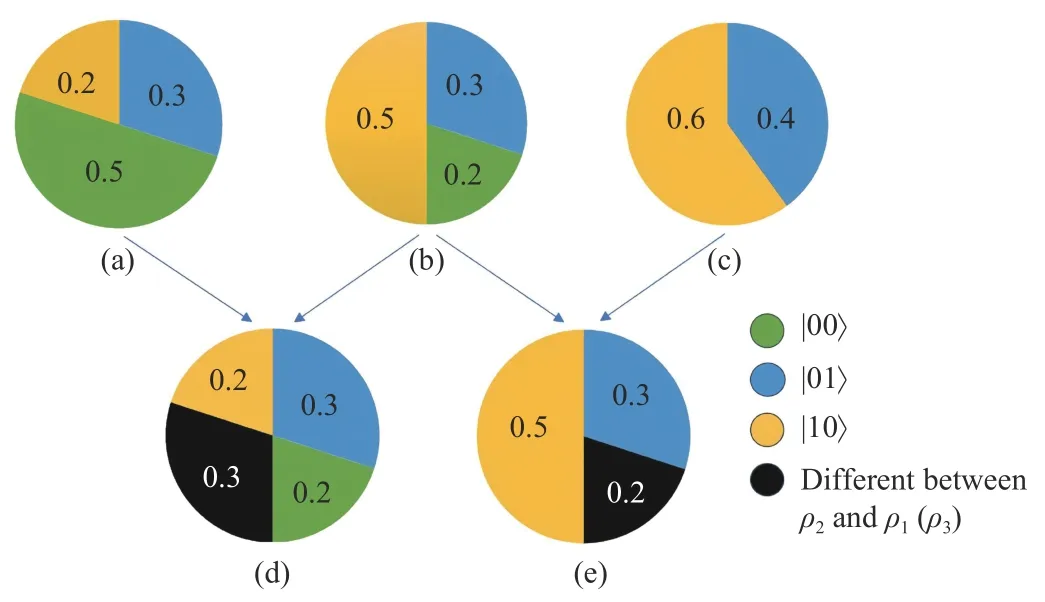
Fig.2.Visualization of Example 1 under x=0 .(a) Quantum state ρ1;(b) Quantum state ρ2;(c) Quantum state ρ3;(d) Similarity and different between ρ1 and ρ2;(e) Similarity and different between ρ2 and ρ3.

In Figs.2(d) and 2(e),the black part represents the different parts between two quantum states,and the color part represents the similarity parts between two quantum states.Obviously,ρ3is more similar to ρ2than ρ1.Therefore,FUJandFAproduce counter-intuitive results.

When fidelity is naturally extended from pure state to mixed state,i.e.,F1(ρ,σ)=tr(ρσ),unsatisfactory results are obtained.For example,when ρ=Id/d,it is easy to get thatF1(ρ,ρ)=tr(ρρ)=1/dinstead of 1,that is,F1is not self-similarity.Therefore,Jozsa [24] used the transition probability of the mixed state defined by Uhlmann [25] to define the fidelity of the mixed state.However,the U-J fidelity requires one to calculate or measure traces of square roots of matrices.This is not trivial in the case of large or infinite density matrices.Hence,Wanget al.[30] proposed an alternative fidelity as shown in (2) by the normalized Hilbert-Schmidt inner product,without calculating the square root of matrices.In addition,there are some alternative fidelities as mentioned above.Nevertheless,the above fidelities have limitations in some cases,as shown in Example 1 and Section IV.Therefore,we define a novel fidelity called QTC fidelity.

B.Definition of the QTC Fidelity Measure

Definition 2:Letρandσbe two density matrices of quantum states,the quantum Tanimoto coefficient fidelity measure between them is defined as

in whichtrdenotes the trace operation.

Equation (15) can also be written in the form of

tr(ρ−σ)2in (16) is known as the Hilbert-Schmidt distance,which is one of the prominent and natural choices to quantify the separation between quantum states.tr(ρσ) is a measure of the overlap between quantum states.Consequently,the overlap and separation between the quantum states are taken into account in the QTC fidelity.Compared with other fidelities,QTC fidelity takes into account the separation between quantum states for the first time,which will make QTC fidelity perform better in measuring similarity.As mentioned earlier,when ρ=Id/d,F1(ρ,ρ)=tr(ρρ)=1/dinstead of 1.This is becausetr(ρσ) is a measure of the overlap between quantum states.It is found that the separation between two same quantum states istr(ρ−ρ)2=0,therefore,FTC(ρ,ρ)=1 in this case.

Equation (15) is applied to any quantum state,including pure state and mixed state.For two pure states |ϕ〉 and |φ〉,the QTC fidelity measure between them also can be calculated by

For any pure state |ϕ〉 and mixed stateρ,the QTC fidelity measure between them becomes

Next,we will discuss some properties of QTC fidelity measure.

C.Properties of the QTC Fidelity Measure

1) Basic Properties:The QTC fidelity measure satisfies the following Jozsa’s axioms:

a)FTC(ρ,σ)∈[0,1],FTC=1,if and only if ρ=σ;

b)FTC(ρ,σ)=FTC(σ,ρ);

c)FTC(UρU†,UσU†)=FTC(ρ,σ) for all unitaryU.

Proof:

a) Note that in (16),sincetr((ρ−σ)2+ρσ)≥tr(ρσ)≥0,0 ≤FTC(ρ,σ)≤1.FTC(ρ,σ)=1 if and only if ρ=σ.

b) Sincet r(ρσ)=tr(σρ) ,FTC(ρ,σ)=FTC(σ,ρ).

c) It can be easy obtained:

QTC fidelity satisfies three axioms of Jozsa’s axioms,except for the third axiom of (5),which is because QTC fidelity takes into account the separation between quantum states.In addition,it is pointed out in [42] that the third axiom of Jozsa’s axioms is superfluous.Like U-J fidelity,the proposed QTC fidelity measure belongs to 0 to 1.If the two quantum states are more similar,the value of the QTC fidelity measureFTCis closer to 1.When the two quantum states are the same,the separation between them is 0,so the QTC fidelity between them is 1.When the two quantum states are orthogonal,the overlap between them is 0,so the QTC fidelity measure between them is 0.Compared with U-J fidelity and A-fidelity,QTC fidelity does not need to calculate the square root of the matrix.In addition,since QTC fidelity considers both the overlap and separation between quantum states,QTC fidelity can better measure the similarity between quantum states.

2) Concavity Property:First,we discuss whether the QTC fidelity measureFTCsatisfies concavity or convexity.To judge whether QTC fidelity meets concavity,we only need to prove whether the following equation is true:

By numerical calculations,we find that the above inequality is satisfied for most matrices ρ1,ρ2,andσforp1+p2=1.However,the violation can also be found.The simplest demonstration can be given if ρ1=I2/2,ρ2=|0〉〈0| and σ=|1〉〈1|f orp1,p2∈(0,1).Here,states |0〉 and |1〉 are orthogonal andI2is the 2×2 identity matrix.To show the violation,let

It is obvious that

That is to say,the QTC fidelity measureFTCsatisfies neither concavity nor convexity.Through calculation,it can be found that in this counterexample,Because QTC fidelity considers the separation between quantum states,and in this example,1−p/2 ≥p/2,the separation accounts for the main part betweenandσ,a smaller fidelity value is obtained,that is,Therefore,in this example,QTC fidelity violates concavity,but this does not affect the similarity between quantum states measured by QTC fidelity.In fact,some fidelity measures do not satisfy with concavity [26],[30].

3) Multiplicativity Under Tensor Products:In contrast with U-J fidelity,the QTC fidelity measureFTCis not tensor products,i.e.,FTC(ρ1⊗ρ2,σ1⊗σ2) ≠FTC(ρ1,σ1)FTC(ρ2,σ2).However,it is found that,like U-J fidelity,the QTC fidelity measure remains unchanged when an uncorrelated ancillary stateτis appended to each of them:

Consequently,QTC fidelity measure satisfiesFTC(ρ⊗τ,σ⊗τ)=FTC(ρ,σ)for any uncorrelated ancillary stateτ.

IV.NUMERICAL EXAMPLES

Existing fidelities may have certain defects in measuring similarity.This section compares QTC fidelity with other fidelities through several numerical examples to reflect the effectiveness of QTC fidelity.

Let us come back to three quantum states ρ1,ρ2,and ρ3in Example 1.By (15),the QTC fidelity between quantum states can be obtained as shown in Fig.3.

Fig.3.The results of fidelity measure of FTC between quantum states in Example 1.

TABLE I SEVERAL QUANTUM STATES

From Figs.1 and 3,compared withFUJandFA,FTCshows reasonable measurement results,and does not require computing the square root of the density matrices.FTC,FN,FW,andFEall indicate that no matter howxchanges,ρ3is always more similar to ρ2than ρ1.As the previous analysis,FUJandFAproduce counter-intuitive results because they only consider the overlap between quantum states.QTC fidelityFTCconsiders both overlap and separation,which will lead to better measurement results,as shown in the following examples.

Example 2:Several quantum states are given in Table I.In Table I,ρ1is a pure state |000〉 .ρ2is a mixed state with a probability of 0.9 being |000〉,and a probability of 0.1 being|111〉,while ρi(i∈[3,8]) has a probability of 0.1 being |000〉,and the remaining degree of uncertainty 0.9 is allocated to more quantum states orthogonal to |000〉.For example,the uncertainty of 0.9 is assigned to four quantum states |001〉,|010〉,|011〉 and | 100〉 that are orthogonal to | 000〉 in ρ5.

The calculation results of fidelity between quantum states in Table I are shown in Fig.4.Fig.4(a) is the fidelity between ρ1and other quantum states,and Fig.4(b) is the fidelity between ρ2and other quantum states.

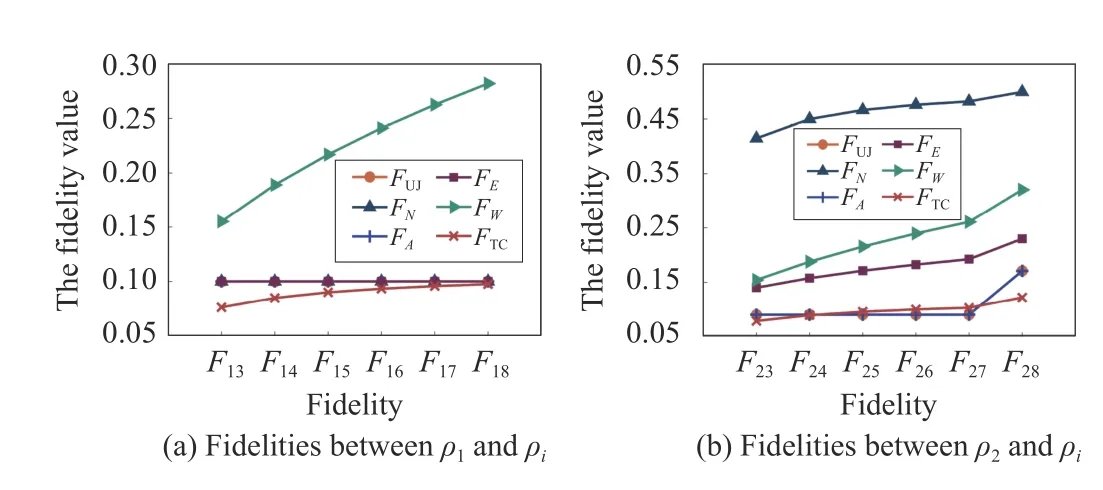
Fig.4.The results of fidelity between quantum states in Example 2.F13 represents the fidelity between ρ1 and ρ3.

From Fig.4(a),FUJ,FN,FAandFEget the same result,that is,the similarity between ρ1and ρi(i∈[3,8]) is considered to be the same.FTCandFWshow that the similarity between ρ1and ρiincreases with the increase ofi.For fidelity between pure state and mixed state,FUJ,FN,andFEonly consider the overlap between quantum states.Although the overlap between ρ1and ρi(i∈[3,8]) is the same,the separation between them decreases asiincreases.Therefore,FTCincreases asiincreases.

In contrast,from Fig.4(b),except between quantum states ρ2and ρ8,FUJandFAbetween ρ2and other quantum states remain unchanged.Nevertheless,the measurement results ofFTC,FN,FWandFEare that with the increase ofi,the similarity between ρ2and ρiincreases.It can be seen from Table I that with the increase ofi,the uncertainty of 0.9 is allocated to more quantum states,and the probability distribution between ρ2and ρiis gradually approaching.Therefore,with the increase ofi,the similarity between ρ2and ρishould increase,so the results ofFTC,FN,FWandFEare more reasonable.In this example,FUJandFAonly consider the overlap between quantum states.Since the quantum states in ρi(i∈[3,7]) are orthogonal to |111〉,the values ofFUJandFAremain unchanged,while ρ8contains | 111〉,so the values change.

In addition,it is found that the QTC fidelity measure can be a good measure of the difference between the superposition state and the mixed state.The specific discussion is given in Example 3 below.

Example 3:Consider the following quantum states:

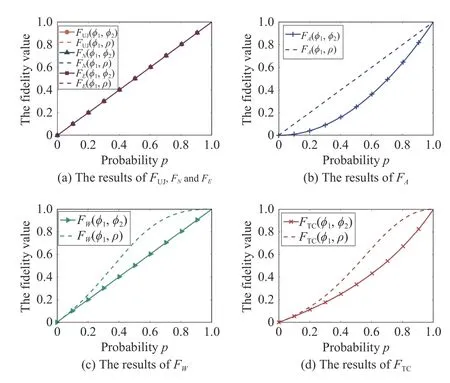
Fig.5.The results of fidelity between quantum states in Example 3.

From Fig.5(a),for fidelity between ϕ1and ϕ2,and fidelity between ϕ1andρ,FUJ,FEandFNget the same results.This shows thatFUJ,FEandFNcannot reflect the difference between superposition state and mixed state.The reason is thatFUJ,FEandFNonly consider the overlap between quantum states in this case,and the overlap between ϕ1and ϕ2is consistent with the overlap between ϕ1andρ,but the separation between quantum states is ignored.As can be seen from Figs.5(b)−5(d),FTC,FAandFWgive different results.For the same quantum state ϕ1,FTCbetween the superposition state ϕ2and the pure state ϕ1is less thanFTCbetween the mixed stateρand the pure state ϕ1.This is caused by the interference of the superposition state.Conclusions similar toFTCare also reflected in the results ofFAandFW.In addition,it is worth noting that compared with other fidelities,QTC fidelity shows nonlinear results,which can better reflect the overall similarity.

Example 4:Let two quantum states be expressed as

To study the influence of variablexand dimensionnon the fidelity,we changexfrom 0 to 1,and varynfrom 1 to 50.The results of fidelity betweenρandϕare shown in Figs.6−8.Sinceρis a mixed state andϕis a pure state,FUJ,FNandFEget the same results,FUJ=FN=FE=tr(ρϕ),as shown in Figs.6(a)−6(d).Figs.7(a)−7(d) are the results ofFTCbetweenρandϕ.Figs.8(a)−8(d) are the results ofFW.For the infinite density matrix,it is not trivial to calculate square root of matrices,and the previous Examples 1 and 2 have shown limitations ofFA.Therefore,FAwill not be discussed in this example.

Whenx=1,no matter how the dimensionnchanges,ρis always equal toϕ,so the value of fidelity is 1.ρcan be expressed as

Therefore,whenxincreases from 0 to 1,the similarity betweenρandϕincreases under the same dimension.In addition,whenxis constant,the similarity decreases with the increase ofn,because the difference between quantum states increases with the increase of dimension.

From Figs.6 and 7,FTC,FUJ,FNandFEreasonably reflect the similarity betweenρandϕ.However,from Fig.8,whenxis fixed,FWdoes not always decrease with the increase ofn.For example in Fig.8(b),asxis 0.3982,FW(ρ,ϕ)=0.9219 whenn=8,andFW(ρ,ϕ)=0.9707 whenn=33.

To better reflect the influence of dimensionn,we takex=0.2,and the change of fidelity value with dimensionnis shown in Fig.9.Whenxis fixed at 0.2,FTC,FUJ,FNandFEdecrease as the dimensionnincreases,whileFWfirst decreases and then keeps increasing asnincreases.In fact,whenxis fixed,FTC,FUJ,FNandFEdecrease monotonically with increasingn,which is easily proven to get true.But obviously,FWis not monotonic.Since the difference between quantum statesρandϕincreases asnincreases whenxis fixed,the similarity decreases,and the results ofFTC,FUJ,FNandFEare more reasonable in this case.

V.THE PROPOSED DISCRIMINATION COEFFICIENTS BASED ON QTC FIDELITY

To measure the difference between quantum states,we define the following discrimination coefficients based on the QTC fidelity measure:

It can be seen that these coefficients are inversely proportional to the QTC fidelity measureFTC.The minimum value of these coefficients is 0 whenFTC=1,that is,when the two quantum states are completely consistent.These coefficients get the maximum value whenFTC=0 .SinceFTC(ρ,σ)=FTC(σ,ρ),these coefficients satisfy symmetry.Therefore,these coefficients can reflect the difference between quantum states.Moreover,to know whether these coefficients meet the metric properties,we only need to verify whether these coefficients satisfy the triangle inequality

Fig.6.FUJ, F N and FE between quantum states in Example 4.

Fig.7.FTC between quantum states in Example 4.

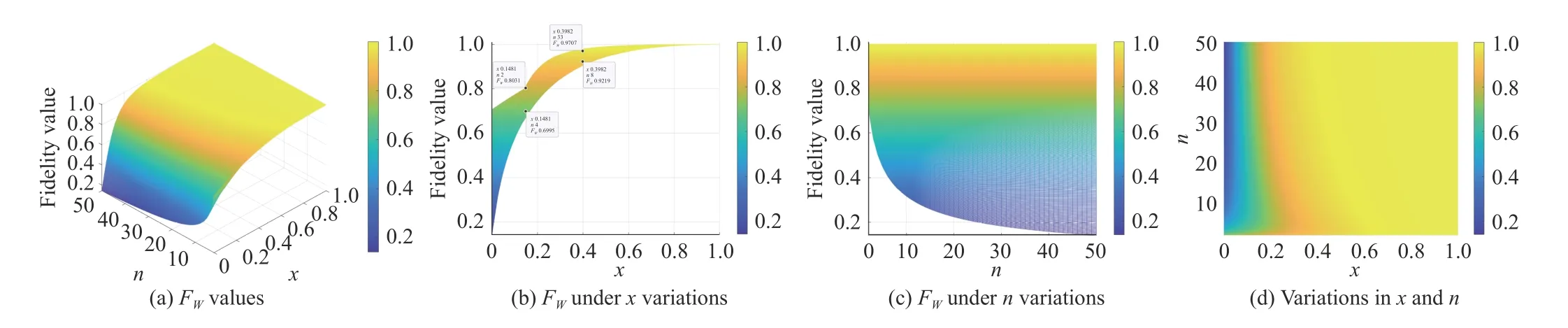
Fig.8.FW between quantum states in Example 4.

Fig.9.The value of fidelity between ρ and ϕ varying with dimension n when x=0.2.

TABLE II THE RESULTS OF TRIANGLE INEQUALITY FOR

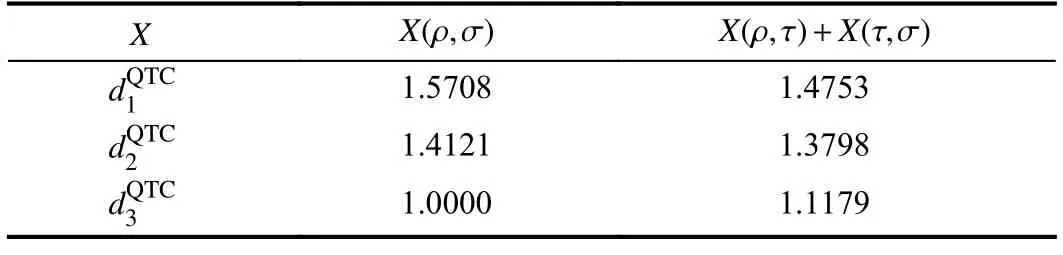
TABLE II THE RESULTS OF TRIANGLE INEQUALITY FOR

Theorem1 (Schoenberg) [43]:Letχbe a nonempty set andK:χ×χ →R a function such thatK(x,y)=K(y,x) andK(x,y)≥0 with saturation if and only ifx=y,for allx,y∈χ.If the implication

This follows straightforwardly by exploiting the zero-sumproperty of the (real) coefficientsciand the linearity of the trace:

Fig.10.The value of distance between two quantum states ρ=a nd σ=p|0〉〈0|+(1−p)|1〉〈1|.

VI.APPLICATION IN ENTANGLEMENT MEASURE

The core of quantum information theory is quantum entanglement,that is,the ability of composite quantum systems to show nonlocal correction.As a basic resource of natural properties,quantum entanglement is as important as energy,entropy,and some other basic resources.In recent years,people have done a lot of work to better understand the nature of entanglement [45].Quantum entanglement is one of the most peculiar properties in quantum in quantum physics,and it is also an important part of the emerging field of quantum information theory and processing.It can be used to achieve physical tasks that cannot be achieved by classical systems such as quantum communication [46],quantum coding [47] and quantum computing [48],[49].Therefore,the task of describing and quantifying entanglement has become one of the prominent themes of quantum information theory.At present,many methods have been developed to measure entanglement.In this section,we apply the proposed QTC fidelity to measure entanglement.

From the perspective of entanglement,quantum states are divided into entangled and disentangled states.For disentangled states,its entanglement is 0,which is defined as [22]

Quantum entanglement measure was introduced in [22],and it can be briefly described as follows: The entanglement of a composite quantum stateσcan be given by the minimal distance between it and a disentangled state

The above entanglement measurement method can measure two subsystems of arbitrary dimensions,but for clarity,we will measure the amount of entanglement of a state of two spin-1/2 states.[22] points out that,for state of two spin-1/2 states,we only need convex combinations of at most 16 pure statesto represent ρ ∈

Eachpican be obtained using the parameterization

and

where αi,βi, ηi,µiand Φiare arbitrary values in [0,2π].It is not difficult to find that up to 1 5+16×4=79 real parameters are needed to completely describe a disentangled state in this case.

Random search for 79 parameters would be very inefficient.Fortunately,forX2,we know that the quantum state and the disentangled state are the most similar when the distance is the smallest.As the quantum state moves away from the disentangled state,the distance will gradually increase.Therefore,we can use the gradient descent method to search for this minimum.The idea is that givenσ,we start with a randomρ,which means that 79 parameters are randomly generated.Then we calculateE(σ),as well as small variations of the 79 parameters ofρ,to obtain the approximate gradient ofE(σ) at the pointρ.Then,we move opposite to the gradient to obtain the nextρ,and repeat this process until the minimum value is found.The process is shown in Fig.11.

Fig.11.The minimum distance between separable state and entangled state is found by gradient descent.

To show the effectiveness and practicability of the proposed method to measure entanglement,let us consider the family of states introduced in [50]

in which 0 ≤p, α ≤1 and the states |00〉,|01〉,|10〉,and|11〉form the standard basis.

To demonstrate the effectiveness and practicability of the proposed entanglement measurement in this paper,we will use the novel methods proposed to analyze how the entanglement degree of the quantum state in (40) changes with the changes ofpandα,and compare with the Bures distance.For the quantum state in (40),when α=0 or α=1,the quantum state is σ=p|11〉〈11|+(1−p)|01〉〈01| andσ=p|00〉〈00|+(1−p)|10〉〈10|,respectively.In this case,there is no entanglement in the quantum system,and the results are shown in Fig.12.Next,we will analyze the more general case of the effect ofpandαon the quantum state in (40).

First,we analyze the effect ofpon the degree of entanglement.We set α=0.75 and letpvary from 0 to 1.Then use the gradient descent method to find the minimum value ofX2(ρ,σ)corresponding to eachppoint.Due to the influence of learning rate and termination conditions in the gradient descent algorithm,we can only get several groups of similar results.Therefore,we use variance diagram to visualize the results,and get the result in Fig.13.As shown in Fig.13,the proposed method of measuring entanglement successfully finds the disentangled state,that is,whenp=1/2,the degree of entanglementE=0.As the quantum state moves away from the disentangled state,the value of entanglement gradually increases,and the entanglement reaches its maximum value atp=0 andp=1.

Fig.12.Entanglement for the state in (40).

Fig.13.Entanglement for the state in (40),with α=0.75.

Then,we setp=0.9 and letαvary from 0 to 1.The entanglement results of the quantum state in (40) are shown in Fig.14.It can be seen from the results in the figure that whenthe value of entanglement is the largest.Moreover,compared with the Bures distance,the novel method obtains a larger value when α=When α=0 and α=1,there is no entanglement in the quantum state,which is consistent with the previous analysis.Consequently,the method proposed in this paper can measure the entanglement of quantum states well.

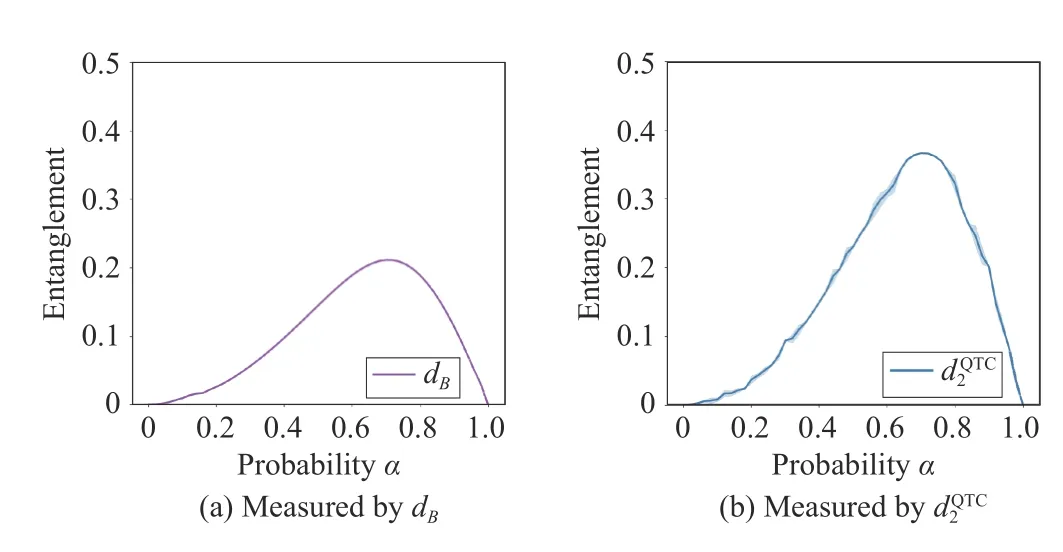
Fig.14.Entanglement for the state in (40),with p=0.9.

VII.CONCLUSIONS

In this paper,a new fidelity called quantum Tanimoto coefficient fidelity was proposed.Compared with U-J fidelity,QTC fidelity measure does not need to calculate the square root of the matrix.Unlike other fidelities,QTC fidelity not only considers the overlap between quantum states,but also takes into account the separation between quantum states for the first time,which leads to a better performance of measure.Several concrete examples show that the QTC fidelity measure can better measure the similarity between quantum states.Then,we discussed the properties of the QTC fidelity measure.The trade-off,however,is that the QTC fidelity measure does not satisfy the concavity.In addition,based on QTC fidelity measure,we also proposed several discrimination coefficientsthat measure the difference between quantum states.Moreover,through analysis,it is proved that the discrimination coefficientis a true metric.Finally,we applied the proposed discrimination coefficients to measure the entanglement of quantum states to show their practicability.