Robust Consensus Tracking Control of Uncertain Multi-Agent Systems With Local Disturbance Rejection

Pan Yu,Kang-Zhi Liu,,Xudong Liu,Xiaoli Li,,Min Wu,,and Jinhua She,

Abstract—In this paper,a new distributed consensus tracking protocol incorporating local disturbance rejection is devised for a multi-agent system with heterogeneous dynamic uncertainties and disturbances over a directed graph.It is of two-degree-of-freedomnature.Specifically,a robust distributed controller is designed for consensus tracking,while a local disturbance estimator is designed for each agent without requiring the input channel information of disturbances.The condition for asymptotic disturbance rejection is derived.Moreover,even when the disturbance model is not exactly known,the developed method also provides good disturbance-rejection performance.Then,a robust stabilization condition with less conservativeness is derived for the whole multi-agent system.Further,a design algorithm is given.Finally,comparisons with the conventional one-degree-of-freedom-based distributed disturbance-rejection method for mismatched disturbances and the distributed extended-state observer for matched disturbances validate the developed method.

I.INTRODUCTION

COOPERATIVE control of multi-agent systems receives more and more attention from scientific and engineering communities owing to its extensive applications in various fields such as unmanned aerial vehicles (UAVs) [1] and satellite formation flying [2].One critical issue arising from the cooperative control is the consensus problem,of which the objective is to develop an appropriate protocol such that all agents reach certain quantities of interest by exchanging information from the agent and its neighbors [3].

Many works have been conducted on consensus control.An output-feedback protocol without controller interaction was developed for homogeneous agents [4].A consensus controller was developed for homogeneous multi-agent systems with heterogeneous disturbances [5].AnH∞consensus control method was addressed for discrete-time multi-agent systems under network imperfections and external disturbances[6].For multi-agent systems,of which agents have nonidentical dynamics,the protocol could be more complex.A PIbased consensus control protocol was discussed for heterogeneous multi-agent systems over directed graphs [7].A distributed optimal consensus control algorithm was developed for continuous-time multi-agent systems [8].An output feedback control scheme was proposed to study theH∞consensus problem of linear discrete-time multi-agent systems [9].However,the aforementioned results on consensus problems are with exactly known agent dynamics.

As is well known,parameter perturbations,unmodeled dynamics,and other factors make it difficult to establish an accurate mathematical model of a plant.So,it is of practical importance to design a robust controller for all possible models [10].However,the system design is more challenging for heterogeneous multi-agent systems with uncertainties due to the complex dynamics and the coupling among agents [11].

Using the state information of neighbors,a robust tracking protocol was presented for multi-agent systems in the presence of matched parameter uncertainties [12].By resorting to the classic robust output regulation theory [13],the internal model method was widely employed to deal with the consensus control of multi-agent systems with time-invariant parameter perturbations [14],[15].As for dynamic uncertainties,a robust stabilization condition was given for multi-agent systems with identical additive uncertainties over indirect graphs[16].A robust protocol without controller interaction was developed to cope with nonidentical uncertain dynamics over directed graphs [17].However,the robust condition was conservative without utilizing the frequency characteristics of dynamic uncertainties.Moreover,only multi-agent systems free from disturbances were discussed.

Disturbances are ubiquitous in practice,which degrade control performance and may even sabotage the consensus task.As a result,disturbance-rejection strategies are necessary.Compared with the one-degree-of-freedom(1-DOF)-based control,two-degree-of-freedom(2-DOF)-based one has more design flexibility,thus enabling better handling the trade off of control performance [18].By using the relative state information of state observers and disturbance observers,distributed disturbance observers were designed for homogeneous multiagent systems with identical disturbances in [19].Since the states of the observers are not physical but artificial,they can incur additional communication complexity and load [20].A distributed extended-state observer was developed for homogeneous multi-agent systems in [21].But it only works for matched disturbances.When the states of agents are known,a finite-time output consensus protocol was studied for a second-order multi-agent system with mismatched disturbances[22].However,not all the states of agents were available in general.It is more natural and practical to use the output information.A distributed consensus method was addressed for a kind of nonaffine systems with nonvanishing disturbance,but the information of the disturbance input channel was required[23].

The equivalent-input-disturbance (EID) approach is widely used for disturbance rejection,which estimates the effect of disturbances on the system output channel and compensates it on the control input channel [24],[25].It is effective for both matched and mismatched disturbances.Moreover,the design of EID estimators does not require the input channel information of disturbances,the availability of system states,and the differentiation of measured outputs.In other words,only the system output is needed for EID estimation.

In this paper,the EID approach is extended to the distributed consensus tracking control of multi-agent systems with heterogeneous uncertain dynamics,aiming at realizing a more effective disturbance rejection.The exchange information among agents is only the relative outputs.Unlike the conventional 1-DOF-based distributed control strategies,an extra degree-of-freedom is utilized for disturbance estimation and rejection.Different from the distributed extended-state observer [21],the developed generalized EID estimators are able to deal with heterogeneous disturbances.To the best of the authors' know ledge,this work is the first attempt to investigate robust distributed consensus tracking control of multiagent systems with nonidentical dynamic uncertainties and disturbances over directed graphs.

The main contributions of this work are listed as follows.

1) A new consensus tracking protocol with 2-DOF is devised.To be specific,a distributed controller is designed for consensus tracking,while local generalized EID estimators for disturbance rejection.

2) The condition for local disturbance rejection is derived.That is,each agent needs only to deal with the disturbances subject to itself,without worrying about the ones interfering with the neighbors.

3) Regardless of disturbances input channels,asymptotic disturbance-rejection performance is theoretically guaranteed when an internal model of disturbances is incorporated.Moreover,the developed method also provides good performance for unknown disturbances.

4) A robust synchronization condition with less conservativeness is developed for the closed-loop multi-agent system,which is easy to check.

The rest of this paper is organized as follows.Section II describes the concerned problem.A consensus protocol is developed in Section III.Sections IV and V analyze the consensus tracking and disturbance-rejection control for a multiagent system.Section VI presents a robust stabilization condition and a design algorithmis given in Section VII.A case study for verification is shown in Section VIII.Finally,Section IX gives some concluding remarks.

In this paper,Rm×pdenotes the set of real matrices withmrows andpcolumns;C denotes the set of complex numbers;0 denotes appropriately dimensioned zero matrix;Indenotes an identity matrix of sizen,andnis usually omitted when it is obvious;z(s) is the Laplace transform ofz(t);when the meaning is clear,the argumentssandtare omitted;a systemG:=(A,B,C,D) is also denoted byG(s):=D+C(sI−A)−1B;the Kronecker product of two matricesAandBisA⊗B;given a column vectorψand a diagonal matrixξ,ψ=col{ψ1,...,ψN} and ξ=diag{ξ1,...,ξN} meanψiis thei-th element ofψand ξiis thei-th diagonal element of ξ,respectively;∥G∥∞is theH∞norm ofG(s);and λ (A),d et(A),and r ank(A) denote the eigenvalue set,the determinant,and the rank of the matrixA,respectively.

II.PROBLEM DESCRIPTION

Consider a set of uncertain agents perturbed by disturbances.Thei-th agent is

whereGn,iis the nominal dynamics;zi,wiare the input,output of the multiplicative uncertaintyW∆i,respectively;andi=1,...,N.Denoteuiandyias the input and output of the actual systemG i,respectively,then we have

The uncertain dynamicsW∆iof thei-th agent (1) may be caused by parameter perturbations (due to fuel burning,payload variation,etc.),neglected dynamics,modeling error,or other unspecified effects.It accounts for the heterogeneity of the multi-agent system.For the sake of design,the following assumption is usually made.

Assumption 1 [10]: W∆ican be described by a stable rational function.

Further,rewriteW∆ias

whereWiis the bound of the uncertainty and it captures the spatial and frequency characteristics [26];and ∆iis the normalized uncertainty satisfying ∥ ∆i∥∞≤1.

For later use,let δi=∆iziand denote the state-space representations ofW∆iandW i,respectively,as

A state-space description of the nominal systemG n,i(s) is

Froma practical point of view,if the disturbance reflects certain dynamics and environment of the considered system,it is natural to assume that the disturbances associated with the agents are different [27],[28].Further,when the disturbance model is known [29],we assume thatdiis generated by

whereAd,iandCd,iare constant.The disturbancedican be polynomials or exponential functions of time.That is to say,it can be unbounded.

For later use,define

wherex0∈is the states,andA0andC0are known constant.The dynamics (9) is also denoted as the leader when the agents (1) are denoted as followers.

Letv={1,...,N} be a node set and ε ⊆v×vbe a directed edge set,respectively.The interaction of theNuncertain agents are described by a directed graph G=(v,ε),where a node denotes an agent and an edge (i,j)∈ε implies thej-th agent can obtain information from thei-th agent fori,j=1,...,N.Define the associated adjacency matrix as A=[ai,j]N×N,whereai,i=0,ai,j=1 if (j,i)∈ε,andai,j=0 otherwise.Let Ni={j:(j,i)∈ε} be the neighboring node set of thei-th node.The corresponding Laplacian matrixforj≠i.Denote the diagonal matrix B=diag{b1,...,bN} to describe the interconnection between the reference exosystem(i.e.,the leader) and thei-th agent (i.e.,thei-th follower).If the reference exosystem is accessible directly to thei-th agent,bi=1,otherwisebi=0 .Define a graphwhich is obtained by attaching the reference exosystem and its outgoing edges to G.Thus,the interaction among the agents and the reference exosystemis indicated by

For later use,define

The following assumptions are made:

Assumption 2 [13],[30]:For the systemG0(10),(A,B) is controllable and (A,C) is observable.

Assumption 3 [13]:All the eigenvalues ofAd(8) andA0(9)are in the closed right-half plane (RHP),i.e.,

Definition 1 [26]:For a systemG:=(A,B,C,D),its system matrix is

IfPG(z0) loses its normal rank atz0∉λ(A),thenz0is a transmission zero of the systemGby Lemma 3.29 of [26].Further,we have

Assumption 4 [13]:For the systemG0in (10),

Assumption 5:All the modes of the disturbances are different from those of the reference,i.e.,

Assumption 6 [31]:The directed graphhas a spanning tree and the leader is its root node,namely,B ≠0.

Definition 2 [13],[32]:Let

whereqiis a square matrix andhiis a vector such that(qi,hi)is controllable or observable.The pair (q,h) is said to incorporate ap-copy internal model ofA0,if the minimal polynomial ofA0equals the characteristics polynomial ofqi,fori=1,...,p.

Remark 1:Assumptions 2–4 are standard to ensure the solvability of the linear robust output regulation problem by using centralized control methods [13].Assumption 5 is made just for simplicity.When it does not hold,there exist common modes for the reference andi-th disturbance exosystems.After removing the common modes and obtaining a new disturbance exosystem,Assumption 5 always holds for the resultant new disturbance exosystem.Assumption 6 ensures that the reference is available to each agent indirectly or directly,which is standard for consensus tracking control problem[31].

III.CONSENSUS PROTOCOL

The configuration of the developed consensus tracking control is shown in Fig.1.It mainly contains four parts.Specifically,they are internal models,state observers,generalized EID estimators,and state-feedback control,respectively.

To achieve consensus tracking,an internal model of the referencergiven by the leader is constructed as

wherexr,iis the state,andArandBrare compatibly constant matrices.The 2nd term is for reference tracking and the 3rd term is for consensus control.Noting (13) utilizes the relative output information among neighbors,it is thus distributed.

Based on the nominal dynamics of the agents,a Luenberger state observer is constructed as follows:

Fig.1.Configuration of consensus tracking control of 2-DOF nature.

When the modes of the disturbances are known,a generalized EID estimator is constructed to achieve complete disturbance-rejection control for thei-th agent.According to Fig.1,thei-th generalized EID estimator is

As we can see,the internal models and state-feedback control constitute a distributed controller for consensus tracking in the outer loop of feedback control.The disturbance estimation and compensation control is in the inner loop.As a result,the developed protocol has 2-DOF.

IV.DYNAMICS OF MULTI-AGENT SYSTEM

Let the state estimation error be

A combination of (2),the second equations of (6) and (14),and (18) yields

Substituting (17) into (14),and invoking (19),we have

Combining with the second equation of (15),substitution of(17) into (6) gives

According to (18),(20),and (21),we have

A combination of (15) and (19) yields

From(13),(21),(22),and (23),we obtain the following augmented system of thei-th agent:

Grouping all agents together,a compact form of the multiagent system(24) is

where the notations are given by (26).

V.CONSENSUS CONTROL PERFORMANCE

By the superposition of linear systems,the consensus control performance of the uncertain multi-agent system(27) is analyzed independently from two aspects.They are consensus tracking and disturbance rejection,respectively.

A.Consensus Tracking

Letdi=0,∀i=1,...,N.We have the following lemma for robust consensus tracking control.

Lemma 1:Let the pair (Ar,Br) incorporate annz-copy internal model ofA0.Under Assumptions 3 and 4,the developed multi-agent system free from disturbances asymptotically achieves robust consensus tracking when the whole system is robustly stabilized.

The proof can be completed by following similar lines of the proof of Theorem1 in [20].

B.Disturbance Rejection

Letr=0.A combination of (27) and (29) gives the following whole multi-agent systemG c:

By the matrix inversion lemma,we have

By the matrix inversion lemma,we have

where

With (12) in Assumption 4,A+BKP−LiC−sIin (43) does not lose the normal rank ofPK,i(s) fors∈Under Assumption 5 and according to Lemma 1,Ar−sIalso does not lose the normal rank.Therefore,only ifPL,i(z0) loses its normal rank,loses the normal rank.

Combining with (45) and (46),(Ae,i,Ce,i) should incorporate at least annz-copy internal model ofAd,ito such thatloses its normal rank regardless ofBd,i.

For simplicity,the following assumption is made.

Assumption 7: n d,i=1 fori=1,...,N.

Remark 2:Since the input channel of the disturbance is unknown,by the homogeneity and superposition of linear systems,there is no harmassumingn d,i=1.

With the above preparation,we have the following theorem on the disturbance-rejection performance of the whole multiagent systemG c(31).

Theorem1:Letr=0 ,(Ae,i,Ce,i) incorporate annz-copy internal model ofAd,ifori=1,...,N.If the whole multi-agent system(31) is stable,then the outputsyiof all agents achieve asymptotic consensus in the face of the disturbancesdiregardless ofBd,i.

Proof:Combining with Propositions 1 and 2,if the whole multi-agent system(31)is stable,thenis a transmission zero of the system(41).Whennd,i=1,z0is also a blocking zero by (11) in Definition 1.According to(32)–(41),the outputs ofGcapproach zero underdby the final-value theorem.Therefore,the multi-agent outputsyiachieve asymptotic consensus of zero under any unknownfori=1,...,N.

Remark 3:With the developed consensus tracking control protocol,Theorem1 show s the disturbance rejection of the multi-agent system with heterogeneous dynamic uncertainties breaks down into that of each individual agent.This reduces greatly the complexity of system design.Further,regardless of disturbance input channels,the developed method guarantees asymptotic disturbance-rejection performance when an internal model of a disturbance is known.On the other hand,when an internal model of step signals is adopted,the generalized EID estimator is actually the conventional EID estimator.Therefore,the developed method is also effective for unknown matched and unmatched disturbances.

By Lemma 1 and Theorem1,the consensus tracking and disturbance-rejection performances are guaranteed as long as the whole multi-agent system is stabilized.Hence,the remainder focuses on the condition of robust stabilization.

VI.ROBUST STABILIZATION

As stated in Lemma 1 and Theorem1,as long as the multiagent system is robustly stabilized,the robust consensus tracking performance is ensured.Thereby,the robust consensus tracking problem is simplified to the stabilization of the developed closed-loop multi-agent system in this section.

Since exogenous signals are irrelative to the stability of linear systems,letr=0 anddi=0,∀i=1,...,Nfor simplicity.A combination of (27) and (30) gives

where

The above closed-loop multi-agent system(47) is used for stability analysis.

For later use,rewrite

With the above preparation,a condition for robust stabilization of the whole 2-DOF-based multi-agent system(47) is derived.

Further,(56) can be replaced by

The block diagram of the transfer matrix (sI−Af,i)−1from τ1to τ2is illustrated in Fig.2,in which the upper part is exactly ρi.Note thatWiand ∆iare stable.By the small gain theorem[10],ifis stable and (54) holds for alli=1,...,N,then the transfer matrix (sI−Af,i)−1from τ1toτ2(sI−Af)−1is also stable.As a result,g2=0 has no roots in the is stable.Consequently,the diagonal transfer matrix closed RHP.

By the determinant identity (A.12) in [33],we have

Fig.2.Block diagram of(sI −Af,i)−1 from τ1 to τ2.

Let

By the matrix inversion lemma,we have

where Θ is defined in (50).A combination of (64) and (66)gives

Rewriteg3=g4g5g6,where

Further,let

Then we have

wherefis defined in (52).Therefore,

Remark 4:The robust consensus control performance of the perturbed multi-agent system with nonidentical dynamic uncertainties is guaranteed by the developed protocol of 2-DOF nature.To be specific,Lemma 1 clarifies the performance requirement of asymptotically consensus tracking and Theorem1 gives that of asymptotic disturbance rejection.The control gains to be determined are (KP,Kr) and (Li,Be,i).The robust stabilization is guaranteed by Theorem 2.

Remark 5:In Theorem 2,the stability ofand (54) are necessary and sufficient for the robust stabilization of every single agent without information exchanging,while (55) and(56) (or (57)) are related to the communication topology.Owing to the control structure of disturbance rejection,f(s) is irrelevant to the parameters of the generalized EID estimators.This is one of the features of the developed 2-DOF-based method and it greatly reduces the computation complexity.

Remark 6:By utilizing the frequency characteristicsWof dynamic uncertainties,the developed robust stabilization condition (Theorem 2) is less conservative than that of [17].Different from the conventional 1-DOF-based distributed consensus tracking and disturbance-rejection control,the developed new consensus control method has a 2-DOF nature,which enables a better performance design.Specifically,the developed method uses the inner loop for local disturbance rejection and the outer loop for distributed consensus tracking,while the conventional one deals with distributed consensus tracking and disturbance rejection in the same control loop.Moreover,unlike the distributed extended-state observer [21],the developed method does not incur additional communication load and is able to deal with heterogeneous disturbances.Furthermore,from the aspect of feedback control,local generalized EID estimators have a faster response,i.e.,better performance of disturbance rejection.

VII.DESIGN ALGORITHM

First,a proposition is given for system design.

Since the technique used for this proof is similar to that of Lemma 1.26 in [13],it is omitted.

A design algorithm is now summarized based on Lemma 1,Theorems 1 and 2.

Design Algorithm for the multi-agent system(1) with heterogeneous dynamic uncertainties and disturbances:

Step 1: Choose (Ar,Br) to incorporate annz-copy internal model ofA0.

Step 2: Calculate the gains (KP,Kr) such thatis Hurwitz.

Step 3: Choose (Ae,i,Ce,i) to incorporate annz-copy internal model ofA d,iandC e,iwith full row rank.

Step 4: Design the gains(Li,Be,i) such thatis Hurwitz.

Step 5: Check if the robust stability condition listed in Theorem 2 holds.If yes,end the design;if not,return to Step 2 or Step 4.

Remark 7:The above algorithm is developed to obtain the control gains (KP,Kr) and (Li,Be,i) such that Theorem 2 holds.A stable matrixin (37) is obtained by following Steps 2 and 4.According toof (37),regarding [KP Kr] as a state feed back control gain,it is clear that the other two matrices inare a controllable pair provided Assumptions 2 and 4 hold.Similarly,according to Proposition 3,the matrix pair inof(37) is observable.So,many methods like optimal control can be used to design the control gains.

VIII.CASE STUDY AND VERIFICATION

In this section,a case study and comparisons with other methods are given to show the advantages of the developed method.

A.Case Study

The nominal dynamics of the agents is the linearized longitudinal dynamics of the YF-22 research UAVs with airspeed 42 m/s and at about 310 maltitude above sea level [27].Denotevi, αi,qi,θi,ui,dias the speed,angle of attack,pitch rate,pitch,stabilator incidence angle,and disturbance of theith agent,respectively.Letxn,i=Then the nominal dynamics can be described by (6).The parameters were identified as follows [34]:

Note that the nominal dynamics has a pole at the origin.To obtain a robust system design,unmodeled dynamics are considered for these agents.The weighting functions of the uncertain dynamics are

The communications among agents are shown in Fig.3.

Fig.3.Communication graph.

The reference and disturbances are,respectively,

Assume the model of the leader is known.As for the disturbances,only the model ofd3is known.With appropriate initial states,randd3can be given by

The other disturbances are zeros.It can be verified that Assumptions 2–5 hold.

Here,the linear quadratic regulation method is adopted to compute the control gains.SetAr=A0,Br=The weight matrices to adjust (KP,Kr) are chosen as

This gives

Although the information ofd2is unknown,we treat its dynamics as an integrator and takeAe,2=0,Ce,2=1 in the design of the corresponding generalized EID estimator.TakeAe,3=Ad,3andCe,3=Cd,3.By trial and error,for a fast response of disturbance-rejection control,the weights corresponding to the states of the local generalized EID estimator should be large.As a result,the weight matrices to adjust(Li,Be,i) fori=2,3 are selected as

The resultant gains are

Considering no disturbances are imposed on thei-th agent fori=1,4,5,6,there is no need of EID estimators for these agents.We just focus on the design of their observers.The weighting matrices to adjustLi,i=1,2,4,6,are

which give

The corresponding norms in Theorem 2 are

As we can see,the robust synchronization condition is satisfied.

The simulation result is shown in Fig.4 where the initial states are assumed to be zeros and ∆iare chosen randomly as

The root mean-square error

is used to evaluate the disturbance-rejection performance,whereei=yi−r.As we can see from Fig.4,for the uncertain multi-agent system(76) and (77),during [25 s,36 s],the developed method achieves a good disturbance-rejection performance for the unknown disturbanced2;during [36 s,45 s],it achieves asymptotic consensus tracking control of (78) and disturbance-rejection control ofd3.Further,theRMESis 0.0113 for the developed method.

Fig.4.System responses of generalized-EID-based consensus tracking control for mismatched disturbances.

B.Comparison With Distributed Disturbance-Rejection Methods

First,the developed method is compared with the conventional 1-DOF-based distributed disturbance-rejection method.The exchanging information among neighbors is the relative outputs,which is the same as the developed method.For a fair comparison,the control gains are designed at the same level with the developed method.The consensus errors are shown in Fig.5.TheRMESis 0.0996,which is 8.8148 times of the developed method.Hence,the developed method has a much better disturbance-rejection performance.

Fig.5.Consensus errors of conventional 1-DOF-based distributed disturbance-rejection method for mismatched disturbances.

The distributed extended-state observer [21] of active disturbance rejection control is also used to compare with the developed method.In addition to the relative outputs,extra exchanging information,i.e.,the relative output error of the agent and its observer,is incurred in the distributed extendedstate observer.Since the distributed extended-state observer only works for homogeneously matched disturbances satisfying the Assumption 4 of [21],we modify the disturbance input channelsBd,2,Bd,3in (76),and the disturbancesd2,d3in (79)as

The other parameters are the same as (76)–(78).After the redesign for the multi-agent system,the consensus errors of the two proceeding methods are shown in Fig.6.TheRMESis 0 .0227 for the developed method with local generalized EID estimators and 0.0397 for the method based on the distributed extended-state observer.This shows the disturbance-rejection performance of the developed local generalized EID estimators is also better than the distributed extended-state observer.

All in all,the developed method is superior to the two distributed control methods.

IX.CONCLUSION

A 2-DOF control structure was devised for a multi-agent system with heterogeneous uncertain dynamics over directed graphs,which not only simplified design complexity but also had a good disturbance-rejection performance.To be specific,a distributed controller was designed to achieve asymptotic consensus tracking,while a generalized EID estimator was locally and specially designed to approximate asymptotically the disturbances of each individual agent.Then a robust stabilization condition with low conservativeness was derived for the whole multi-agent system by the small gain theorem.Further,a simple algorithm was also developed for system design.Finally,the developed method was validated by a case study and two comparisons with distributed disturbance-rejection methods.

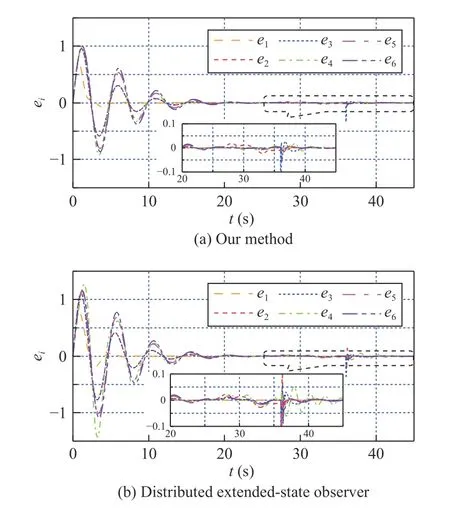
Fig.6.Consensus errors of methods based on distributed extended-state observer and local generalized EID estimators for matched disturbances.

The developed method provides asymptotic stability and performance for the consensus tracking control of multi-agent systems with heterogeneous uncertain dynamics and disturbances.Finite-time [35] or fix-time [36] stability and performance are also of interest and practical in engineering,which will be investigated in the future.