应用兰利法的机电引信逐渐解除隔离试验
2023-03-07李睿成徐蓬朝黄惠东
李睿成,徐蓬朝,2,王 森,梁 统,黄惠东
(1.西安机电信息技术研究所,陕西 西安 710065;2.西北工业大学机电学院,陕西 西安 710072)
0 引言
引信是弹药发火作用的先导装置,安全性和可靠性是引信尤为重要的两项性能指标。目前国内针对引信火工品感度的研究主要集中于引信解除保险距离领域,缺乏对引信内部传爆序列隔爆可靠性的研究。国外针对引信传爆序列的隔爆性能研究早已展开并形成了标准文件[1]。GJB 573B—2020是对引信及其相关部件的性能评估标准[2],首次在国内提出了逐渐解除隔离试验,为引信传爆序列隔离件位置与安全性能评估提供了方法依据,但国军标中仅推荐了用于引信逐渐解除隔离试验的方法,包括概率单位法、兰利(Langlie)法、一次使用变换响应法(OSTR)和勃罗西登法等。上述文献表明,目前国内尚未对逐渐解除隔离试验的方法进行深入研究。针对国内研究不足的情况,本文提出应用兰利法的机电引信逐渐解除隔离试验方法。
1 感度试验兰利法
1.1 兰利法概述
兰利法是1962年由Langlie提出的一种数理统计方法,可看作是一次刺激变换响应法(OSTR)的特例[3],最初用于对50%响应点对应的刺激量进行估计[4-5]。兰利法的试验序列是变步长的,刺激量步长跟随试验进程不断调整,使得试验刺激量很快收敛于感度分布的均值附近[6],适合小样本量试验。
兰利法通常假设感度分布服从正态分布[7-8],通过估计正态分布参数进而估计任意刺激值对应的响应概率或任意响应点。兰利法对于样本均值的估计受初始估计值的影响较小[7-9],但对方差的估计结果则偏低。文献[10]中给出了兰利法服从正态分布和Logistic分布的方差估计偏量修正系数。
1.2 兰利法试验程序
首先需要选择试验上、下极限,使得刺激量为上限xU时全响应、为下限xL时无响应。
以刺激量x1进行第一次试验,记录x1和响应数v1,v1=0或1分别表示不响应或响应。其中x1的公式为
x1=0.5(xL+xU)。
(1)
对于后续试验i=2,3,4,…,用刺激量xi完成第i次试验并记录vi后,观察是否满足试验终止准则。若满足则试验终止,若不满足则进行第i+1 次试验。刺激量xi+1的计算公式为
(2)

试验需要选择一个终止准则,通常选用的终止准则有:1)完成预定的试验量N,N应不少于20;2)预定试验结果序列中出现响应与不响应转换的次数,转换次数应不少于5[10]。此外在达到预定终止条件后,还需通过数据记录表,查找vi=1对应的最小刺激量,作为x1L;查找vi=0对应的最大刺激量,作为x0U。若x0U>x1L,计算区间(x1L,x0U)中刺激量的个数nm,试验完成;若x0U≤x1L,未产生混合结果区,应增加第N+1次试验,将新数据加入数据记录表中,以N+1作为新的N值,并修正x1L和x0U的值,直到x0U>x1L成立,有混合结果区出现,求出nm,试验完成。
2 应用兰利法的机电引信逐渐解除隔离试验方法
2.1 兰利法与机电引信相结合
按照解除隔离过程中隔离件的运动形式,可将机电引信传爆序列机构分为平动式和转动式。两种结构传爆序列在解除隔离过程中均能较为直接地确定爆炸元件之间的相对位置。对于平动式传爆序列,可将试验主要变量设置为隔离件解除隔离过程中的位移,通过增大或减小这一位移,使爆炸元件相互靠近或远离;对于转动式传爆序列,可将试验主要变量设置为两级爆炸元件以及机构旋转轴线所成夹角,通过减小或增大这一夹角,使爆炸元件相互靠近或远离。可对引信传爆序列机构进行适当加工,使其在不影响爆轰传递的前提下便于将爆炸元件固定在某一位置。
根据兰利法的试验程序设置每次试验的刺激量进行试验,观察引信在见证板上产生的痕迹对爆轰传递情况进行判断。依据GJB 573B—2020,传爆序列爆轰传递到隔离件后的任一爆炸元件,并在见证板上产生凹痕,则定义为传递;爆炸元件的烧焦、碳化、金属融化、穿透和变形仅记录结果,不认为产生传递。
试验达到预先设定的终止准则并满足试验完成条件后,试验结束。
针对机电引信的兰利法逐渐解除隔离试验流程如图1所示。

图1 基于兰利法的机电引信逐渐解除隔离试验流程Fig.1 Test procedure of progressive arming test for electromechanical fuze based on Langlie method
2.2 兰利法试验数据处理方法
依据对感度分布模型类的假设,分别进行数据的统计分析。试验假设机电引信解除隔离试验中,爆轰传递与隔离件运动位移的关系服从正态分布,对应的数据统计分析方法如下[10]:
1)总体参数μ和σ
基于试验数据x1,x2,…,xN;v1,v2,…,vN;x1L、x0U;nm、N计算
μ0=0.5(x1L+x0U),
(3)
σ0=N(x0U-x1L)/(8(nm+2))。
(4)
对如下方程组进行求解
(5)
式中,
求得式(5)的解Δμ和Δσ,若满足
|Δμ|+|Δσ|<ε,
(6)
则停步,进而计算
(7)
(8)
若不满足式(6),则令
μ0=μ0+Δμ,
(9)
σ0=σ0+Δσ,
(10)
并重新计算式(5),直到满足式(6)。
总体分布的估计量公式为
(11)
(12)
式中,β为σ估计值的偏量修正系数。
2)p响应点的估计
(13)
式(13)中,μp为N(0,1)的p分位数。
3)响应概率的估计
刺激量为x时,响应概率p的估计计算公式为
(14)
式(14)中,Φ为N(0,1)的分布函数。
3 仿真及试验验证
本文采用的机电引信传爆序列隔离装置为平动式滑块机构,盖板和导爆管壳的材料为钢,滑块和基座的材料为铝合金,盖片的材料为铜,雷管采用LD-14A电雷管,导爆管装药为JH-14C,药量380 mg,密度为1.60 g·cm-3,其结构如图2所示。

图2 引信传爆序列结构示意图Fig.2 Schematic diagram of the structure of the fuze detonation train
在引信解除隔离的过程中,导爆管随滑块在基座上移动,传爆序列由错开运动到直列状态,此时各爆炸元件之间没有隔爆件且呈直线排列,引信处于待发状态,如图3所示。

图3 传爆序列由完全隔离位置到直列位置的变化Fig.3 Transmitting the explosion detonation train from fully isolated position to in-line position
3.1 仿真计算
3.1.1机电引信传爆序列仿真模型
根据试验中使用的机电引信的结构及材料特点,对其传爆序列进行了三维建模及网格前处理。为简化计算量,采用1/2对称模型进行仿真,并对结构部分不影响爆轰传递的结构特征(如螺栓)进行了简化,网格数量总计386 812。机构的仿真模型如图4所示。

图4 机电引信传爆序列机构1/2网格模型Fig.4 1/2 grid model for electromechanical fuze detonation train mechanism
仿真选用多物质ALE算法,建立空气网格进行流固耦合计算,将雷管和空气域网格定义为ALE网格,其余部分为Lagrange网格。
滑块、基座和指示靶材料为铝合金,在仿真过程中使用的本构模型为*MAT_PLASTIC_KINEMATIC;盖板和导爆管壳材料为钢,导爆管盖片材料为铜,选用本构模型为*MAT_JOHNSON_COOK和*EOS_GRUNEISEN;空气的本构模型为*MAT_NULL和*EOS_GRUNEISEN。各类材料参数如表1—表3所示。

表1 铝合金PLASTIC_KINEMATIC材料参数[11]Tab.1 PLASTIC_KINEMATIC parameters

表2 主要材料JOHNSON_COOK模型参数[12-13]Tab.2 JOHNSON_COOK parameters

表3 空气材料模型参数[14]Tab.3 Parameters of air
LD-14A电雷管主要装药为HMX炸药,选用*MAT_HIGH_EXPLOSIVE_BURN作为雷管装药材料模型,*EOS_JWL作为其爆轰产物状态方程,其参数如表4所示。

表4 HMX炸药JWL模型主要参数[15]Tab.4 JWL parameters of HMX
对导爆管装药JH-14C选用Lee-Tarver点火增长模型进行计算,材料模型为*MAT_ELASTIC_PLASTIC_HYDRO,状态方程采用*EOS_IGNITION_AND_GROWTH_OF_REACTION_IN_HE,本文使用的JH-14C炸药点火增长模型参数如表5所示。

表5 JH-14C的点火增长模型主要参数[16-17]Tab.5 Lee-Tarver parameters of JH-14C
3.1.2仿真结果分析
将滑块处于完全隔离位置定为0 mm位置,将滑块直列位置定为20 mm位置。对隔离装置滑块位移分别为15、15.5和20 mm三种情况进行了仿真计算,在导爆管药柱区域选取沿轴线分布的A、B、C、D、E、F六个单元作为观测点,用以观察爆轰传递过程中导爆管装药参数的变化情况,如图5所示。通过观察导爆管装药内部压力变化以及装药单元反应度参数变化情况,判断导爆管装药是否被引爆。

图5 导爆管内部观测点分布情况Fig.5 Distribution of observation points inside the lead explosive
图6、图7为传爆序列直列位置的情况下导爆管药柱在雷管起爆后的压力及反应度变化情况。在传爆序列直列位置,导爆管药柱各观测点压力峰值的最小值为观测点A,出现于1.15 μs时,峰值为5.72 GPa;其余各观测点压力峰值均超过25 GPa。各观测点在2.15 μs后反应度均已达到1,表明此时药柱内部沿轴线均已完全起爆。
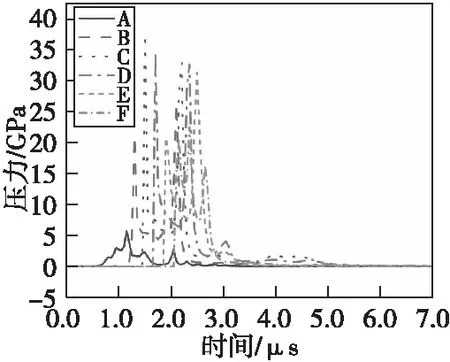
图6 直列位置导爆管装药内部压力-时间曲线Fig.6 Internal pressure-time curves of lead explosive(in-line position)

图7 直列位置导爆管装药反应度-时间曲线Fig.7 Burn fraction-time curves of lead explosive(in-line position)
图8、图9为位移15 mm时导爆管药柱在雷管起爆后的压力及反应度变化情况。位移15 mm时,各观测点压力峰值最大值仅为0.184 GPa,远小于爆轰传递状态下的压力峰值。各观测点的反应度也远小于1。

图8 位移15 mm时导爆管装药内部压力-时间曲线Fig.8 Internal pressure-time curves of lead explosive(15 mm position)

图9 位移15 mm时导爆管装药反应度-时间曲线Fig.9 Burn fraction-time curves of lead explosive(15 mm position)
图10、图11为位移15.5 mm时导爆管药柱在雷管起爆后的压力及反应度变化情况。位移15.5 mm时,观测点A和B的压力峰值分别为9.2和14.8 GPa,但反应度均在14~15 μs内达到1;但观测点C、D和E的压力峰值均超过了25 GPa,且反应度也均在15 μs内达到1;观测点F在计算终止时刻15 μs时还尚未出现压力峰值,反应度数值也未有变化,说明导爆管药被引爆,但是爆轰波在15 μs时尚未传递到观测点F的位置。
对比3种隔爆装置位移的仿真结果可以发现,JH-14C装药在正常起爆情况下,炸药内部的压力峰值能够稳定超过25 GPa,炸药绝大多数单元的反应度都能达到1。在传爆序列直列位置下仿真得到的压力及反应度变化情况与位移15.5 mm时的情况类似,即导爆管药柱起爆;而位移15 mm时压力和反应度参数的变化情况表明此时药柱未起爆。针对本文使用的机电引信传爆序列机构,已解除隔离位置在滑块位移15~15.5 mm之间。

图10 位移15.5 mm时导爆管装药内部压力-时间曲线Fig.10 Internal pressure-time curves of lead explosive(15.5 mm position)

图11 位移15.5 mm时导爆管装药反应度-时间曲线Fig.11 Burn fraction-time curves of lead explosive(15.5 mm position)
3.2 试验及统计分析
3.2.1试验流程
机电引信隔离装置沿直线运动的位移为本试验的主要变量,故将位移x作为试验的刺激量。将滑块处于完全隔离位置定为0 mm位置,将滑块直列位置定为20 mm位置。通过兰利法确定每次试验的刺激量xi,使用精度为0.01 mm的游标卡尺对试验装置内滑块的位置进行测量,并以螺栓固定。
实际试验使用的引信传爆序列实际结构如图12所示。

图12 试验引信传爆序列机构实物Fig.12 Physical mechanism of test fuze detonation train
试验时将引信机构放置在铝合金指示靶上,靶厚为3 mm,试验装置如图13所示。

图13 试验装置Fig.13 Test setup
最终试验总数N=23,x1L=15.41 mm,x0U=15.44 mm,存在混合结果区(15.41,15.44)。在爆轰传递的情况下,指示靶上形成了直径9.5~10.5 mm的通孔;在爆轰未传递的情况下,指示靶上仅形成烧灼痕迹或轻微变形。典型痕迹如图14、图15所示。

图14 指示靶典型痕迹(爆轰传递)Fig.14 Typical marks on witness plate (transfer)

图15 指示靶典型痕迹(爆轰未传递)Fig.15 Typical marks on witness plate (non-transfer)
3.2.2试验数据的统计分析
兰利法逐渐解除隔离试验的试验数据记录如表6所示。
1) 样本总体参数的计算
根据2.2节中的计算方法,求得兰利法试验得到的爆轰传递概率分布的样本均值和方差分别为

(15)

(16)

表6 基于兰利法的引信逐渐解除隔离试验数据记录Tab.6 Test data of progressive arming test based on Langlie method
2)已解除隔离位置的确定
根据式(13)、式(15)和式(16),计算得到95%置信度下使得爆轰传递到隔离装置后下一元件的概率达到0.005对应的滑块位移为
(17)
3)传爆概率的计算
根据式(14)、式(15)和式(16),分别对滑块位移15和15.5 mm时爆轰传递的概率进行计算:
(18)
(19)
将试验得到的爆轰传递概率分布模型与仿真结果进行对比,通过试验数据计算得出的已解除隔离位置为滑块位移15.27 mm处,这与通过仿真结果推得的已解除隔离位置(滑块位移15~15.5 mm)结论相符合。这说明基于兰利法的机电引信逐渐解除隔离试验方法具有一定的准确性。但是在15.5 mm位移时仿真得到的结论是导爆管药柱完全起爆,而通过试验结果计算得到的结论是15.5 mm位移时导爆管药柱完全起爆的概率为0.764 238,这一差异可能由试验测量误差累计效应引起。
根据兰利法试验数据可作试验结果分布图,并可通过曲线拟合得到机电引信爆轰传递概率相对隔离件位移的函数图形,如图16所示。

图16 估计爆轰传递概率相对隔离件位移函数图Fig.16 Estimated burst transfer probability versus interrupter displacement
4 结论
本文提出应用兰利法的机电引信逐渐解除隔离试验方法,该方法将感度试验兰利法与逐渐解除隔离试验相结合,通过正态分布参数对爆轰传递概率与隔离件运动位移关系进行拟合,计算任意刺激值对应的引信作用概率。仿真数据与试验结果表明,应用兰利法的逐渐解除隔离试验方法理论计算值与仿真数据、试验结果相近,该方法可在小样本条件下对引信传爆序列隔爆性能做出评估,可用于指导机电引信隔爆机构与传爆序列设计。
本文不足之处:兰利法在进行感度分布估算时存在对方差估计偏小的问题,在小样本量情况下可能存在估算的解除隔离位移与实际情况有偏差。后续可对兰利法的统计分析过程进行改进,进一步修正其对样本方差的估计偏差,以提高分布估计的准确性。
