基于长短期记忆神经网络的弹丸落点预测

卢新月，祁克玉，2，钱荣朝，李小平，徐国泰

(1.西安机电信息技术研究所，陕西 西安 710065；2.机电动态控制重点实验室，陕西 西安 710065)

0 引言

落点预测是精确制导的关键技术，预测性能直接影响制导弹药的打击精度[1]。经典的落点预测将弹丸运动参数代入飞行动力学模型，通过数值方法迭代计算弹丸的实际落点[2-3]。这种方法计算量大、解算时间长，且容易积累迭代误差，难以满足先进武器的需要。

近年来有学者提出其他预测方法：文献[4—5]将卡尔曼滤波引入落点预测，这种方法直接外推弹道落点，减小了随机噪声对预测的干扰，但预测速度较慢；文献[6—7]通过拟合的方法建立落点偏差的预测模型，能够快速预报落点，但精度不足；文献[8—9]以神经网络为工具建立落点预测模型，避免了积累误差的产生，但在不同环境的适用性方面仍有不足。

长短期记忆网络(LSTM)是一种时间循环网络[10]，被广泛用于航空、道路等领域的序列数据处理。本文针对上述方法时间较长、易积累误差或对气象变化适用性不足的问题，提出基于LSTM网络的弹丸落点预测方法。

1 LSTM网络基本原理

LSTM神经网络是一种特殊的RNN网络，它拥有传统RNN处理序列数据的能力，且改善了RNN网络梯度爆炸的问题。图1是LSTM网络的模型示意图。在LSTM网络的链式结构中，每个神经元通过三个“门限”来增加或删除神经元状态中的信息，如图2所示，Ct-1为上个时刻的神经元状态，Ct为本时刻的神经元状态。

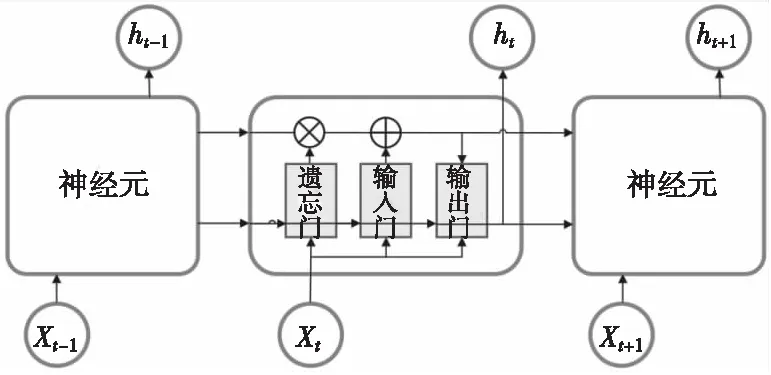
图1 LSTM网络模型示意图Fig.1 Structure of LSTM neural network

图2 神经元状态信息的传递Fig.2 Transmission of neuron state information

“遗忘门”决定了上个时间点的状态信息Ct-1被遗忘还是保留。如图3所示，上一时间点的输出ht-1和当前时间点的输入Xt经过Sigmoid激活函数，输出的结果ft决定了Ct-1被保留多少。若ft等于1，则Ct-1全部被保留；若ft等于0，则Ct-1全部被遗忘。

图3 LSTM遗忘门Fig.3 LSTM forget gate

图4 LSTM输入门Fig.4 LSTM input gate

有了遗忘门和输入门，可以通过式(1)确定新神经元的状态Ct：

(1)

“输出门”决定了神经元的最终输出。如图5，先用ht-1和Xt通过Sigmoid层生成ot，再将ot与之前得到的Ct相乘，作为神经元的输出ht。

图5 LSTM输出门Fig.5 LSTM output gate

由此，LSTM网络可以通过遗忘门、输入门与输出门对状态Ct的影响，决定t时刻遗忘、记忆及输出哪些信息，并将这个状态传递下去，达到记忆长期的重要信息，遗忘短期不重要信息的目的。

2 LSTM神经网络的落点预测

2.1 数据处理

将弹丸落点视为弹丸飞行中各实测参数的非线性方程，则弹丸的射程横偏与实测参数的函数如式(2)所示。

(2)

式(2)中，X和Z相互独立，X为弹丸射程，Z为横偏，R为弹丸位置，V为弹丸速度，m为弹丸质量，ρ为空气密度，τ为虚温，Vw为风速。

考虑实际应用中的弹丸与环境条件，各参数设置为：射角3°～27°，弹丸质量18.5～18.9 kg，虚温250～310 K，空气密度1.17～1.25 kg/m3，风速±20 m/s。通过四阶龙格库塔法解算6D外弹道方程得到弹道数据。

为避免输入数据量级差异过大而影响训练效果，将得到的数据进行归一化，归一化公式为

(3)

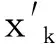
将弹道数据归一化后，随机选取弹道数据的80%为训练集，剩余的20%为测试集，得到用LSTM神经网络进行落点预测的数据集。

2.2 网络结构

LSTM网络是递归神经网络的一种，擅长处理序列数据。通过图6所示的链式结构处理输入序列，Xt是t时刻的输入序列，A是隐含层节点，ht是t时刻的状态。网络的输入除了本时刻的输入Xt外，还有上一时刻的反馈状态ht-1，两者共同进行决策。

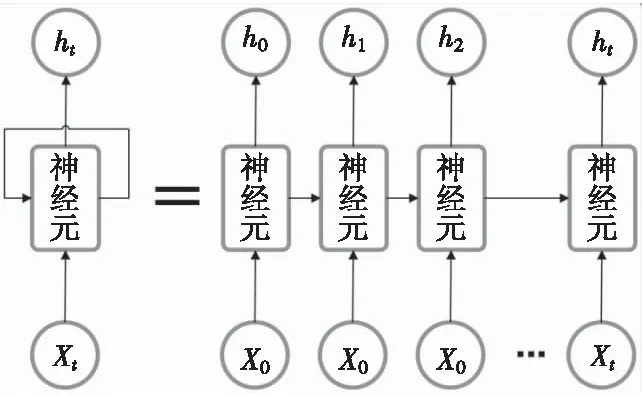
图6 LSTM神经网络链式结构Fig.6 Linked structure of LSTM

用LSTM网络进行落点预测，本质是实现序列的回归，因此网络应当由输入层、LSTM层、全连接层和回归输出层构成。由于射程与横偏是两组相对独立的序列，分别构建射程与横偏的预测网络模型。

对于横偏，构建图7结构的LSTM网络，其中隐含层有60个神经元。

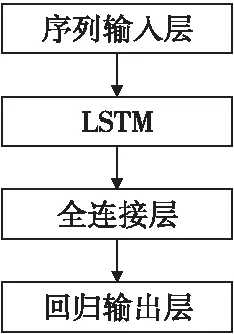
图7 横偏LSTM预测网络结构Fig.7 Structure of LSTM on lateral deviation prediction

对于射程，构建图8结构的LSTM网络，其中隐含层有60个神经元。为防止过拟合，在网络中加入丢弃层，如图9，虚线部分的神经元不更新，这样随机地“暂时删除”一部分神经元，以避免少数的错误输出影响整体网络输出正确结果。

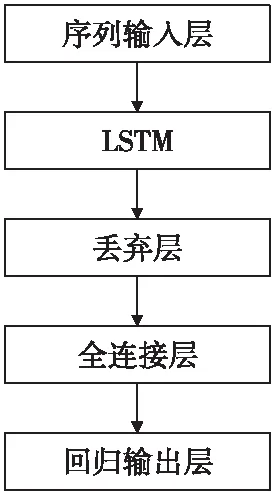
图8 射程LSTM预测网络结构Fig.8 Structure of LSTM on range prediction

图9 LSTM丢弃层结构示意Fig.9 Structure of dropout layer

3 仿真分析

用数据处理得到的数据集对构建的LSTM网络模型进行训练和测试。测试完成后，用数据集之外，射角3°～27°，弹丸质量18.5～18.9 kg，虚温250～310 K，空气密度1.17～1.25 kg/m3，风速±20 m/s范围内的1 000组弹道数据作为验证数据集，分别用训练好的网络进行射程和横偏的预测，并将预测结果与原弹道实际落点进行比较。

3.1 落点预测准确性

分别预测弹丸的射程与横偏，射程与横偏的预测误差如图10与图11，预测误差的最大、最小值与均方差如表1所示。

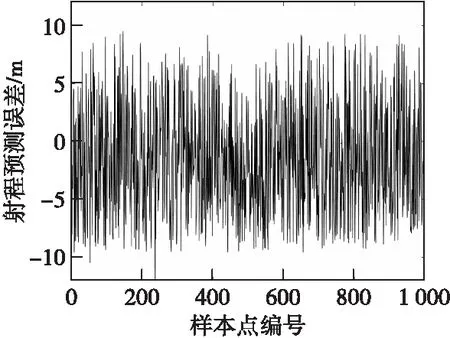
图10 射程预测误差Fig.10 Range prediction error

图11 横偏预测误差Fig.11 Lateral deviation prediction error

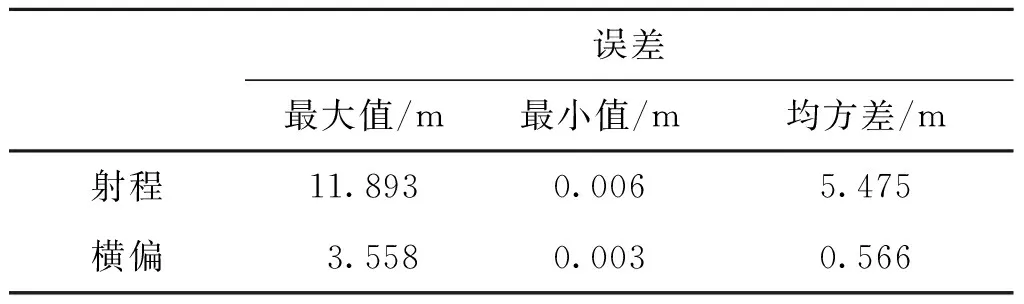
表1 预测误差统计Tab.1 Statistics of prediction error

对于二维弹道修正，一般要求落点预测误差均方差≤10 m即可。由表1的统计结果得知，LSTM预测方法的射程误差均方差为5.475 m，横偏误差均方差为0.566 m，能够以较高的精度进行落点预测，满足落点预测的精度要求。测试结果表明，该方法对于气象条件在虚温250～310 K，空气密度1.17～1.25 kg/m3，风速±20 m/s范围内变化的弹道落点均能达到良好预测效果，具有适用性。

3.2 落点预测快速性

在实际应用中，神经网络的训练是在地面提前完成的，弹上只需装载训练好的网络，因而可以大幅减少运算时间。随机选取训练数据集以外的10条弹道，分别通过数值积分方法和完成训练的LSTM网络计算弹道落点，对比两种方法的运行时间，结果如表2所示。

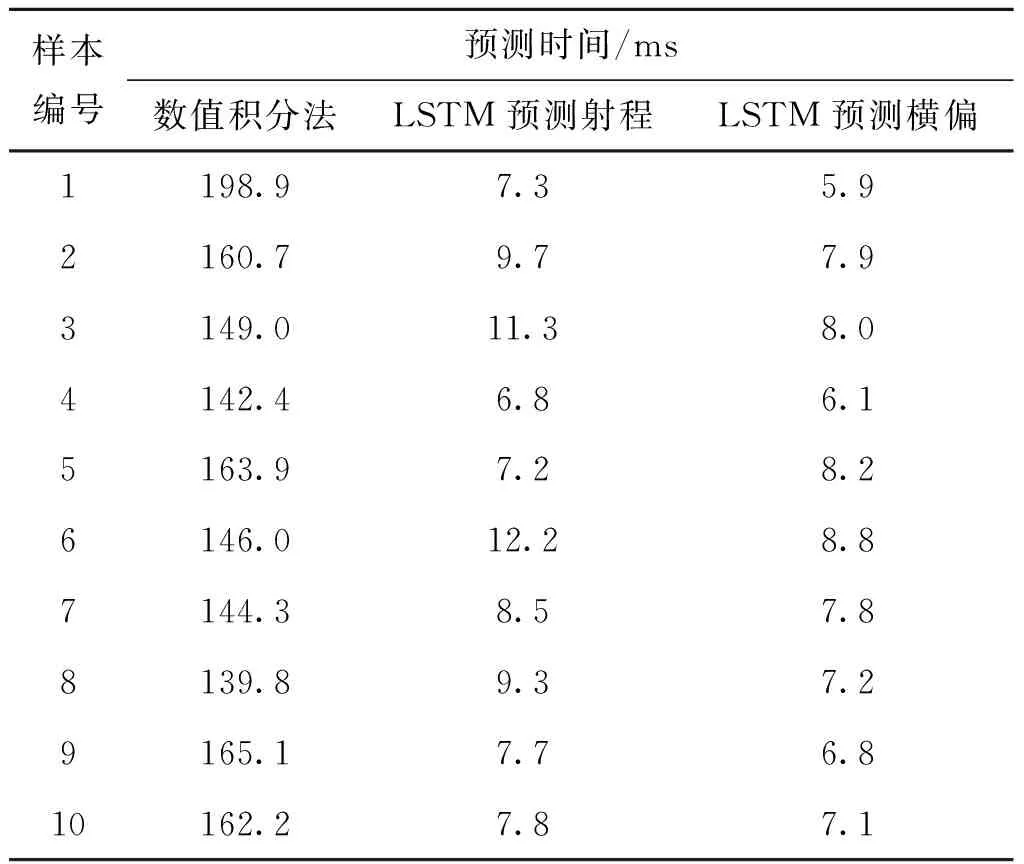
表2 预测时间统计Tab.2 Statistics of predictiontime

由表2统计的预测时间可以计算出，数值积分法进行落点预测的平均时间为157.23 ms，而LSTM方法预测射程平均时间为8.78 ms，预测横偏平均时间为7.38 ms，比数值积分法快一个量级。因此LSTM方法能大幅减少预测时间，可以满足落点预测的快速性要求。

4 结论

为提高落点预测的速度、精度与复杂气象适用性，本文提出基于LSTM神经网络的弹丸落点预测方法。该方法首先建立了基于LSTM神经网络的落点预测模型，然后用不同气象条件下的弹道仿真数据对模型进行训练，最后对训练完毕的网络进行落点预测的仿真测试。仿真结果表明，对于不同气象条件下的弹道，在准确性方面，射程误差均方差为5.475 m，横偏误差均方差为0.566 m，预测精度较高；快速性方面，射程预测平均时间为8.78 ms，横偏预测平均时间为7.38 ms，比数值积分方法快一个数量级。因此，本文提出的方法能够在复杂气象条件下准确预测弹丸落点，且预测速度明显优于数值积分方法，可以为外弹道落点预测的应用提供参考。