声子晶体中低频减振降噪技术及带隙特性研究

胡启国，白 熊，魏 晨，汪柯宇

(重庆交通大学 机电与车辆工程学院，重庆 400074)

0 引言

大型机械装备产生的振动噪声往往呈现中低频特性，这种噪声更加沉闷，难以降噪，而声子晶体技术因其特定频段带隙可设计性的特点，为齿轮箱减振降噪提供新的选择.声子晶体作为近年来用于装备减振降噪研究新热点，已被广泛应用于国防、航天、船舶、交通以及微电子领域.

早在二十世纪八十年代，就有学者提出一种具有特殊带隙特性的功能材料，并将其命名为光子晶体[1,2].到了新世纪，学者在对周期变化的多材料复合结构进行研究时，发现弹性波在这些复合结构中传播时，周期结构内部形成独特的色散关系[3,4]，故此声子晶体的概念得以产生.声子晶体结构因为对弹性波的带隙特性而被广泛运用于机械行业中[5]，更因其轻质、吸能、吸声以及电磁屏蔽的特性，被现代工业认为是当前国际上最具前景的新一代先进超材料[6].声子晶体一般由两种及两种以上材料组合而成，材料组成十分丰富.

经过学者们多年的研究，越来越多材料被用于声子晶体的设计.张赛等[7]选用石英玻璃和水作为一维声子晶体结构组成材料.Hyasse等[8]利用石墨烯-双层半导体制备无限和半无限超晶格.声子晶体带隙特性除了与其组成材料有关外，还会受到不同结构形状的影响.考虑不同的应用场景，学者们开发出多种结构形式的声子晶体，并针对结构参数对带隙影响展开分析.如李夏临等[9]设计了一种二维分布式陀螺结构声子晶体.对晶格常数、散射体尺寸和陀螺式声子晶体的角动量、转动惯量和扭转刚度对带隙特性影响进行了分析.康太凤等[10]设计了一种空心散射体声子晶体.这种声子晶体由四个环氧树脂连接板与空心铅柱组合而成，其中铅柱上附着硅橡胶材料.

考虑应用场景不同，学者们针对不同应用场景对声子晶体进行了设计与研究.许祥曦[11]将桁架管设计为一维声子晶体周期性排列结构形式，用于海洋平台桁架减振系统.Sheikhaleh等[12]利用二维光子晶体加压滤波，基于波长调制方法，提出了一种新型光学微机电系统加速度计传感器.沈惠杰[13]将海水运输管路的振动噪声控制理论与声子晶体带隙特性相结合，基于一维声子晶体结构形式设计出周期性海水管路，使得海水运输管路具有水力噪声带隙特性.

基于现有研究基础，考虑大型机械装备，如大型齿轮箱中低频振动噪声问题，设计了一款包覆魔方型声子晶体结构，并对该声子晶体带隙产生机理，带隙影响因素，传输损耗进行了分析.

1 声子晶体基本理论与结构介绍

1.1 弹性波波动方程

固体介质中的某一点受到外界物理作用扰动的情况下，由于介质的弹性，会使得扰动质点同其周围质点间的弹性力增加.而这种质点的作用持续下去，便会形成从扰动源开始的波动现象.这种现象可以用弹性波波动方程来进行表示：

(1)

式(1)中：ρ为介质密度，u为位移矢量，λ、μ都为Lame系数.而基于Lame定理和Helmholtz证明可以知道，对于任意矢量，在其定义域内有散度存在，则该矢量便可以用一个标量φ的梯度φ和一个矢量位Ψ的旋度×Ψ之和来表示，而弹性波动场正好满足这一条件，因此可以得到：

u=φ+×ψ

(2)

将式(2)代入式(1)中，并进行散度与旋度变换可以得到φ和ψ满足的波动方程：

(3)

(4)

1.2 Bloch定理

(5)

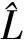
Yk,n(X)=eik×Xuk,n(X)

(6)

式(6)对应其本征值满足：

λk,n=λk+Gm,n

(7)

uk,n(X)对于格矢Rn的平移具有周期性质，同样满足式：

uk,n(X+Rn)=uk,n(X)

(8)

(9)

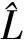
(10)

λk,n=λξk,n

(11)

由式(10)、(11)可以证明，波矢取值在倒格子空间高对称点处，本征场群沿对称面的法向分量取零，本征谱取极值.由此可知，如果想要计算带隙频率范围而进行能带结构计算，任意波矢k只要在不可约布里渊区的边界取值开展计算即可，其中不可约布里渊区如图1中蓝色部分所示.

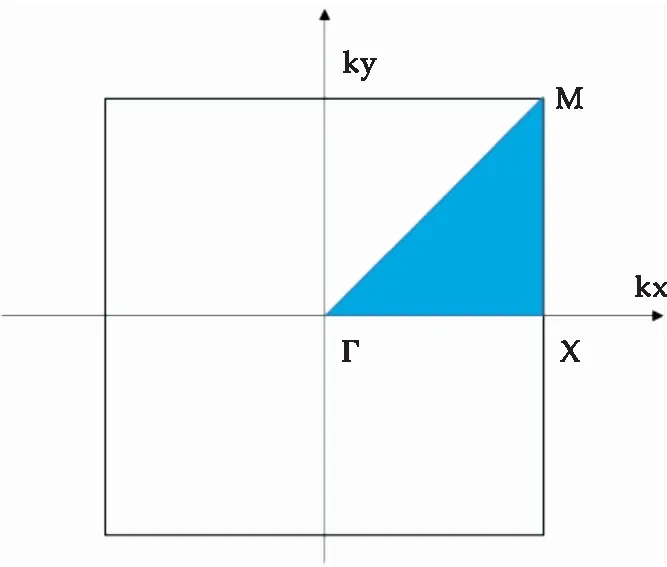
图1 不可约布里渊区示意

1.3 包覆魔方型声子晶体模型

考虑中、低频段噪声更加沉闷且难以降噪的特点，设计了一种包覆魔方型声子晶体结构，如图2所示，该声子晶体单胞结构由两种材料构成，整个声子晶体单胞为立方体结构，各边边长相等.同样内部散射体也为立方体结构，由27个小立方体构成一个类似魔方的立方体结构.声子晶体单胞外层包覆层由硅橡胶构成，中心由金属组成散射体，构成一种可在中低频范围对弹性波进行耗散的局域共振型声子晶体单胞.

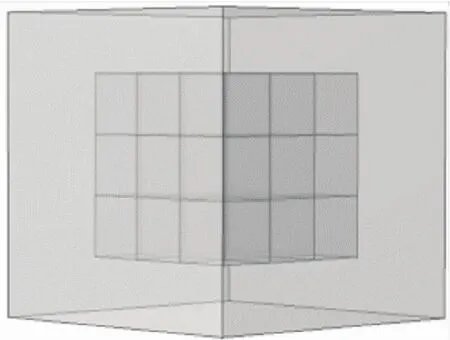
图2 声子晶体单胞结构

2 声子晶体带隙产生机理分析

2.1 声子晶体带隙计算

基于有限元方法，利用Comsol分析软件对包覆魔方型声子晶体带隙进行求解.以晶格常数a为15 mm，散射体尺寸b为9 mm，其中散射体选用钨材料，包覆层选用硅橡胶材料，材料参数如表1所示，对其带隙进行求解.

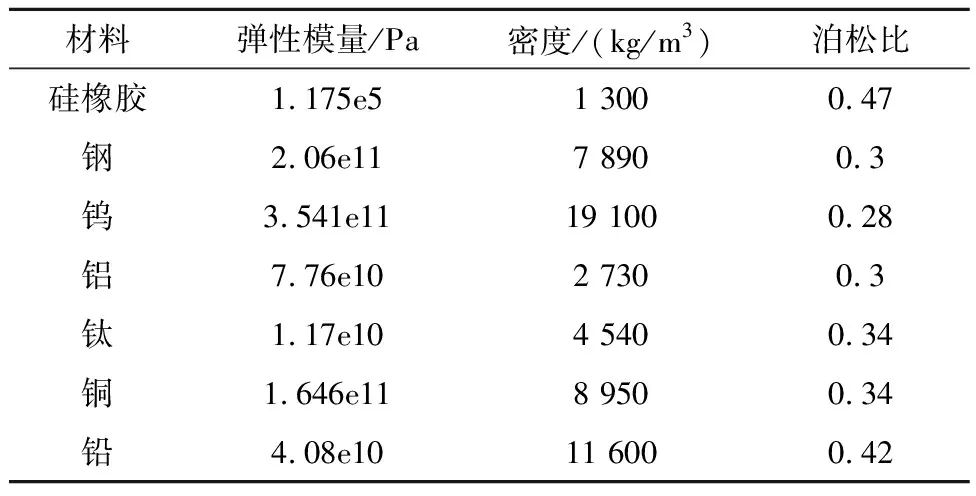
表1 材料参数表

首先，在几何模块中进行建模，并利用材料模块分别对包覆层与散射体进行材料定义.接着添加固体力学物理场，并设置周期性边界条件.由于该声子晶体为立方结构，弹性波从6个面入射，起到耗散弹性波效果相同，因此只对单独一个面设置边界条件.选择周期性边界条件类型为Floquet周期，设置周期矢量kx，ky.最后设置参数化扫描，分别从Γ～X(0～π)，X～M(π～2π)，M～Γ(2π～3π)三个矢量方向对带隙进行扫描，选取了10个特征频率数量，通过软件对声子晶体特征频率进行求解，结合软件自带的参数化扫描功能，即可得到以钨材料为散射体的包覆魔方型声子晶体带隙图，如图3所示.

从图3可以看出，能带在高对称点分开，这是由于长波行波在中低频范围内，其波长远远大于单元结构也即晶格常数的长度，而弹性波在中低频范围内传播与均匀介质相同，能带图呈线性关系.当硅橡胶包覆层中的行波频率接近或者等于散射体共振单元的固有频率时，则散射体共振单元内会发生局域共振.硅橡胶包覆层中的长波与散射体的共振模态相互耦合，绝大部分弹性波能量将被局域在散射体共振单元中，以此实现弹性屏蔽，故此会出现带隙.以钨材料为散射体，硅橡胶为包覆层的声子晶体在166～350 Hz频率范围内产生了完全带隙，如图阴影部分所示

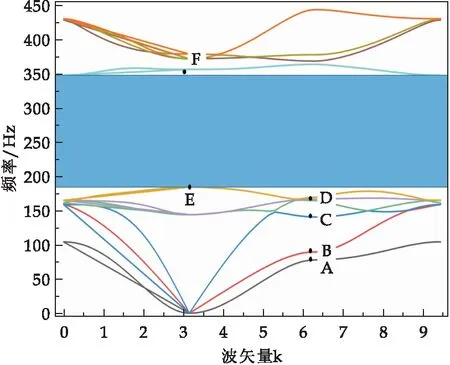
图3 钨散射体带隙结构图

2.2 高对称点振动模态与带隙产生机理

这里可以将声子晶体等效为质量-弹簧系统，如图4所示，当入射弹性波频率处于完全带隙频段内时，入射弹性波会对硅橡胶包覆层产生力F的作用，当弹性波传递到振子Me而使其发生运动，振子Me同样会对硅橡胶包覆层产生反作用力f.基体在两力共同作用下振动，当入射弹性波激励频率与共振单元的固有频率接近时，两作用力反向叠加，包覆层合外力为零.因而包覆层趋于静止状态，入射弹性波被局域化，振动能量无法传播，仅局限于共振单元中，能量被共振单元消耗掉，故而弹性波在完全带隙频段无法传播.

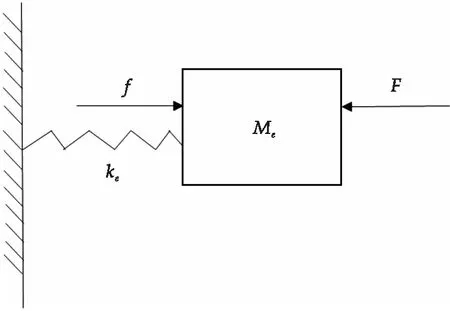
图4 等效弹簧-质量系统

基于声子晶体等效质量-弹簧系统，并对第一布里渊区内的A～F六个高对称点的振动模态进行求解，对声子晶体带隙产生机理进行分析，求解结果如图5所示.其中A、B为弯曲振动模式，A点的频率为78.15 Hz，以y为轴发生弯曲，B点的频率为89.83 Hz，以z轴为中心发生弯曲.此时该局域共振单元振子为硅橡胶包覆层，基体为散射体.散射体受到两侧硅橡胶包覆层的挤压作用，分别z轴正向和y轴正向的移动.当弹性波频率和该局域共振系统固有频率相似，散射体在发生位移后，处于静止状态，此时声子晶体原胞所受合力为零，故不能产生局域共振而耗散弹性波或者声波.

图5 A～F振型图

C～F四个高对称点都为扭转振动模式，C点处的频率为141.02 Hz，在该处声子晶体原胞以y轴中心发生扭转；D、E两点处的频率分别为164.92 Hz、184.62 Hz，都以z轴为中心进行扭转；F点处的频率为347.74 Hz，以x轴为中心进行扭转.C、F点处，共振单元振子为散射体，硅橡胶包覆层为基体，C、F点处分别以y、x为轴发生扭转，扭转带动散射体同时发生扭转，当入射弹性波刚好为这一频率时，激发扭转发生，此时散射体合力为0，故处于相对静止状态，难以产生耗散弹性波的作用.D、E两点处频率时，入射弹性波与两者频率相同时，同样激发扭转发生，但入射频率由于波长的缘故，只激发了外部硅橡胶包覆层处的发生扭转，而散射体相对静止，故同样不能起到耗散弹性波的作用.

3 声子晶体带隙特性影响分析

3.1 材料参数对带隙特性的影响

对于声子晶体，可以把带隙特性影响因素分为两类，分别为材料参数和结构尺寸因素[14,15].现在先从材料因素对包覆魔方型声子晶体进行分析.根据表1数据，选用钢、钨、铝、钛、铜、铅分别作为散射体，得出不同材料下声子晶体完全带隙对比情况，如图6所示.

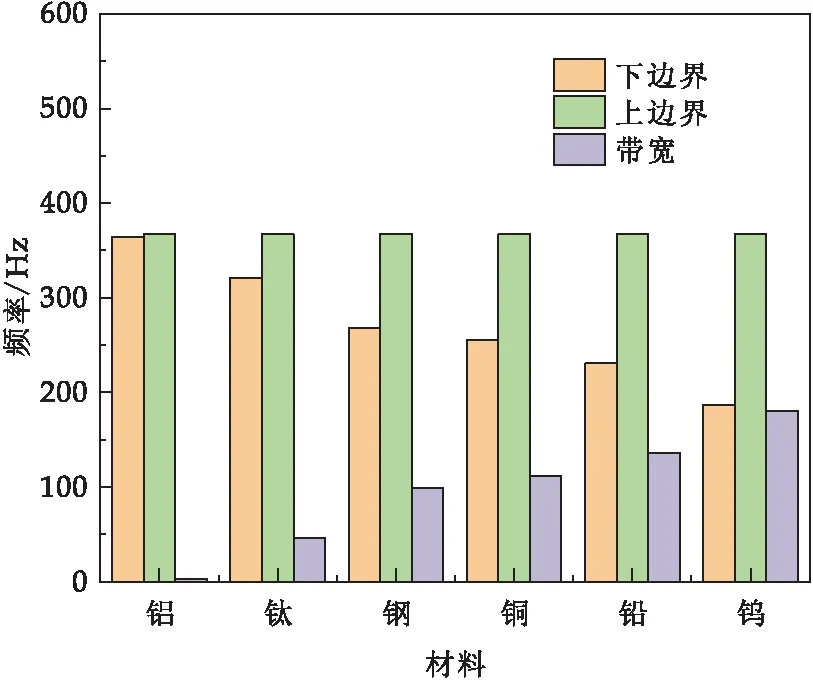
图6 不同材料散射体声子晶体完全带隙对比

从图6可以看出，包覆魔方型声子晶体的完全带隙宽度以钨为散射体时最宽，铝为散射体时完全带隙宽度最小.并且，不同材料完全带隙上边界几乎相同，而完全带隙下边界存在较大的差异.结合表1材料参数数据，发现钨材料的弹性模量与密度皆高于其余材料，可以猜想该声子晶体的完全带隙宽度与材料弹性模量和密度间存在一定关系.为了验证这个猜想，选取以钨为散射体的包覆魔方型声子晶体，开展材料力学参数对完全带隙宽度影响分析，其结果如图7、图8所示.

由图7可知，横坐标为杨氏模量，随着杨氏模量的增加，声子晶体带隙上、下边界几乎保持不变，固可知杨氏模量对该声子晶体带隙影响效果并不明显；由图8可知，横坐标为包覆魔方型声子晶体散射体质量密度，随着散射体质量密度的增加，完全带隙上、下边界都处于减少趋势，并且带宽增宽.故此可以得出结论，声子晶体散射体质量密度对完全带隙有一定影响，但影响范围不大.

图7 散射体杨氏模量对带隙的影响

图8 散射体密度对带隙的影响

3.2 结构参数对带隙特性的影响

除了散射体材料对完全带隙有影响外，声子晶体自身结构参数也会对完全带隙造成影响.这里选取钨材料作为包覆魔方型声子晶体的散射体，分别以该包覆魔方型声子晶体晶格常数、散射体尺寸为变量展开分析，得出结论如图9、图10所示.

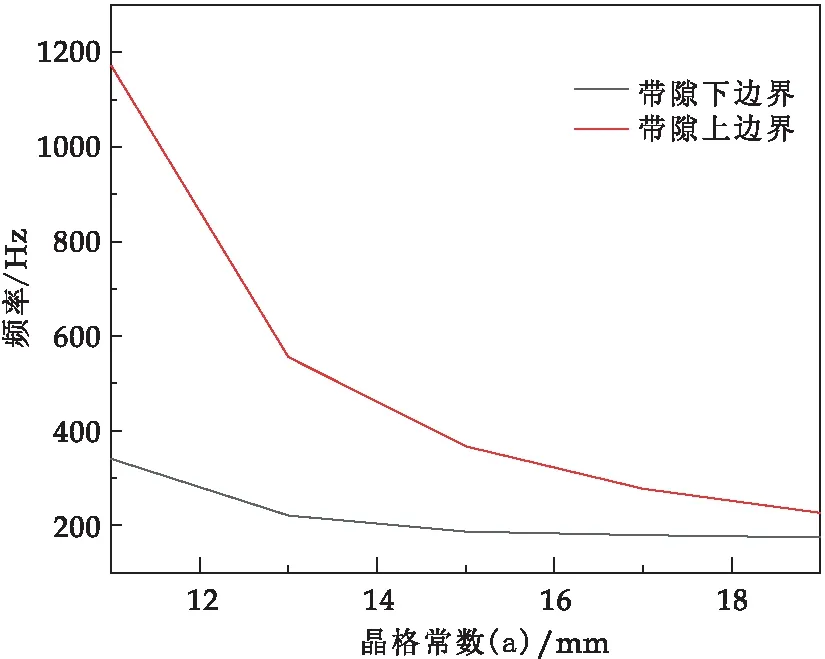
图9 不同晶格常数对带隙的影响

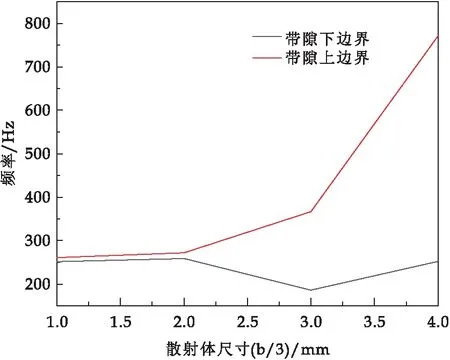
图10 不同散射体尺寸对带隙影响

图9表示不同晶格常数下声子晶体完全带隙变化情况，随着晶格常数的增加，完全带隙上、下边界呈减小趋势.上、下边界对比可以得出，上边界随着晶格常数的增加，数值下降趋势更加陡峭，而下边界数值，相对更加平缓.图10为散射体尺寸对完全带隙影响曲线，包覆魔方型声子晶体完全带隙宽度随着散射体边长的增加而增加，其中声子晶体随着散射体尺寸的增加，完全带隙上边界呈逐渐增加的趋势.随着散射体尺寸的增加，完全带隙下边界呈先减少再增加的变化，其中增加转折点出现在散射体尺寸为3 mm时.从对比分析可知晶格常数和散射体尺寸都对完全带隙有着显著影响.

4 声子晶体弹性波传输损耗分析

4.1 声子晶体板振动响应

为了进一步确定该包覆魔方型声子晶体完全带隙特性，选择晶格常数a为15 mm，散射体尺寸b为9 mm，散射体为钨，包覆层选用硅橡胶，验证包覆魔方型声子晶体减振、降噪能力性能.利用Comsol多物理场分析软件，首先对包覆魔方型声子晶体板进行建模，以声子晶体单胞为基础，利用阵列功能构建10×10的声子晶体板，同时在声子晶体板两侧构建过渡层与完美匹配层，如图11所示.

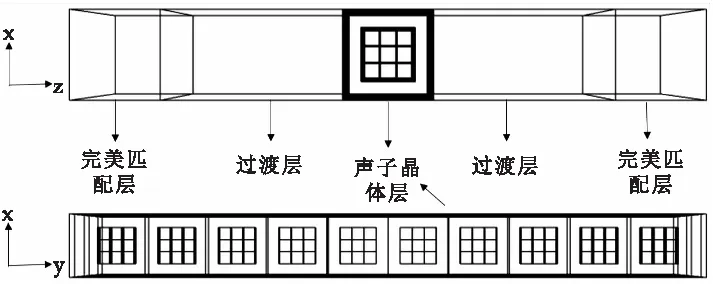
图11 声子晶体板传输损耗仿真模型

通过向z轴正方向给定振动加速度1 m/s2，对传输损耗模型进行求解，可以得到弹性波影响下声子晶体内部振动位移云图，如图12所示.这里选择141 Hz，251 Hz，301 Hz，521 Hz四个激励频率，当激励频率落于声子晶体完全带隙频段范围以内时，弹性波受到声子晶体局域共振的作用，使得弹性波被抑制，反之弹性波则可以顺利通过声子晶体.

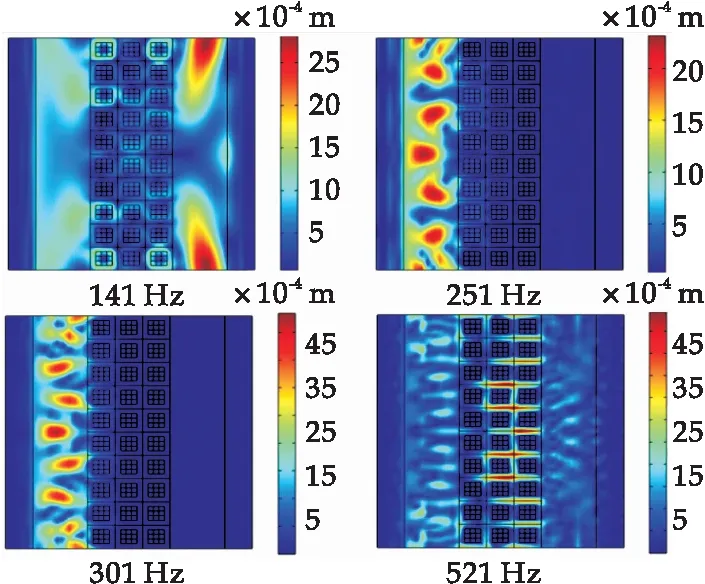
图12 各激励频率下振动位移云图

4.2 不同层数声子晶体板传输损耗对比

对于实际工程应用中，由于现场环境的不同，声子晶体减振、降噪的能力同样也会有所差异[16].为了增强减振、降噪的能力，往往需要使用多层声子晶体结构.为了了解不同层数声子晶体的减振、降噪能力，这里提取了不同层数声子晶体传输损耗曲线，如图13所示.

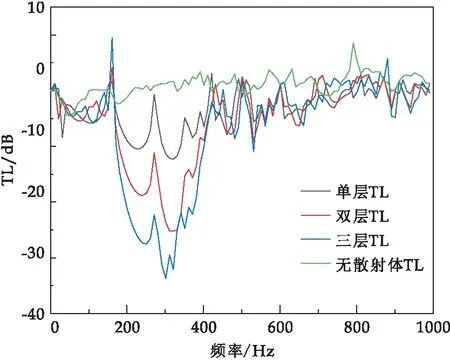
图13 不同层数声子晶体传输损耗对比

由图13可以看出，横坐标为频率，纵坐标为传输损耗TL(Transmission Loss，TL)，在166～350 Hz频段，随着包覆魔方型声子晶体板层数的增加，其传输损耗以每层10～15 dB数值减少.相比较于无散射体的硅橡胶板，其传输损耗效果明显减少.但在160 Hz左右频率范围内，随着层数的增加，出现传输损耗数值的增加的现象.这是由于随着层数的增加，在150 Hz频率左右，声子晶体降噪板和入射弹性波产生整体共振的原因.为了解决这一问题，并优化包覆魔方型声子晶体板的减振效果，引入缺陷型声子晶体板，利用声子晶体板缺陷效应来解决这一问题.

4.3 不同缺陷声子晶体传输损耗对比

所谓声子晶体缺陷，就是在周期排列的声子晶体中出现一点、一条线和一个面的异于其它声子晶体的结构形式，在带隙图上表现出来就是会在其它频段产生完全带隙的现象.这里选用三层声子晶体板，在中间层设置声子晶体散射体尺寸缺陷、声子晶体散射体材料缺陷两种缺陷形式，得出传输损耗曲线如图14、图15所示.

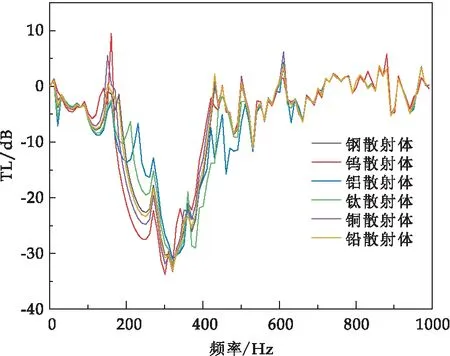
图15 不同散射体材料缺陷传输损耗对比

从图14可以看出，中间缺陷层声子晶体散射体尺寸b为9 mm和b为7 mm时，在频率170 Hz左右产生传输损耗增加的现象，也即出现传输损耗异常，当使用这两种声子晶体降噪板时，在165 Hz频率附近将导致弹性波的增大，也即振动幅度增大.此外，在使用缺陷型声子晶体板后，在频段60～155 Hz范围内，相较于无缺陷声子晶体板，产生了新的完全带隙.散射体尺寸b不同时，产生带隙值不同，当b为11 mm时，产生的最大传输损耗为16.5 dB.通过引入散射体尺寸点缺陷声子晶体单胞，可以有效优化声子晶体弹性波传输损耗异常增加现象，从而提升声子晶体板减振、降噪性能.

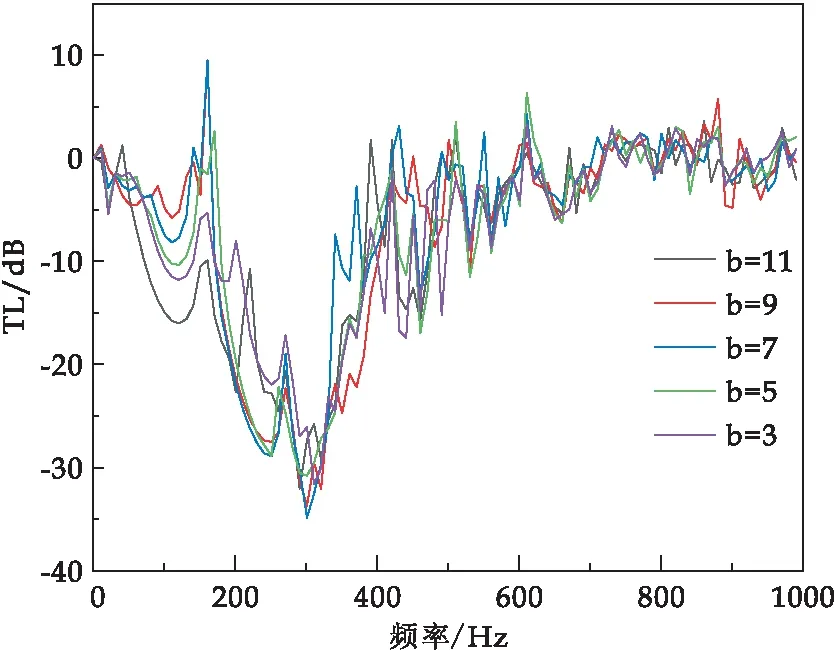
图14 不同散射体尺寸缺陷传输损耗对比

由图15可以看出，当缺陷层散射体材料为钨和铅时，165 Hz附近传输损耗增加.引入铅作为散射体的缺陷声子晶体也出现与无缺陷声子晶体一样的问题，这是由于铅的力学性质，如密度、弹性模量，相较于其它材料更加接近如钨，故此会产生近似的带隙特性.在频率166～350 Hz范围内，也即钨材料包覆魔方声子晶体完全带隙频段范围内，无缺陷声子晶体传输损耗特性表现最佳，随后依次为铅、铜、钢、钛、铝作为散射体的声子晶体单胞.然而在92～160 Hz范围内，传输损耗效果最佳的为铝材料，随后依次为钛、钢、铜、铅、钨，并且以铝、钛、钢、铜为散射体的缺陷声子晶体单胞在这个频段范围内未出现传输损耗增加的现象.为此可以得出结论在钨材料为散射体的声子晶体板中，引入不同材料作为散射体的缺陷声子晶体单胞可以在其它频段产生额外完全带隙，基于这一规律，可以达到额外频段的传输损耗优化效果.

5 结论

(1)提出一种包覆魔方型声子晶体结构，以钨为散射体材料，硅橡胶为包覆层，利用Comsol多物理场分析软件，对带隙进行求解，发现在中低频段(166～350 Hz)产生完全带隙结构；基于该声子晶体对其带隙产生机理进行分析.

(2)从散射体材料参数和声子晶体结构参数对带隙特性的影响进行分析，得出结论：这些参数都对声子晶体完全带隙有着相应的影响，其中晶格常数和散射体尺寸对带隙影响更为明显.

(3)为了验证声子晶体减振降噪性能，搭建声子晶体传输损耗求解模型，分析了不同层数声子晶体传输损耗变化情况，发现每增加一层，声子晶体传输损耗随机减少约10～15 dB.

(4)为了解决随着层数的增加，特定频段传输损耗不降反升的问题，利用散射体尺寸缺陷、散射体材料缺陷对传输损耗进行优化，通过引入缺陷声子晶体解决了传输损耗异常的问题，而且产生了新的完全带隙，使得减振、降噪频段得以扩展.