促进思维进阶的初中数学深度教学改进——以“由所想到的……”专题复习为例*

葛余常 (江苏省泰州医药高新区(高港区)教师发展中心 225300)

1 基本情况

1.1 授课背景和对象

在初三数学一轮“数与式”复习中，教师往往注重“点”状复习方式，只关注知识内容的按序依次展开进行“识记、理解与应用”，未能形成基于富有挑战性的问题进行知识多维整合与关联，未能促进“分析、评价与创造”，从而不能实现由低阶思维向高阶思维进阶．而学生经过初中三年的数学学习，已经初步掌握了一定的数学知识和数学技能，需要在教师的引导下，通过有意义的学习活动来发展高阶思维能力．

1.2 教材分析

教学目标 (1)通过分数类比学习，架构分式的概念、分式的运算、分式方程的复习，提高对所学知识的理解和应用能力；(2)通过分式的生长，抽象拓展分式不等式、分式函数以及构造图形的学习，提高分析、评价和创造等高阶思维能力．

教学重点 创设分式教与学的系统，引导学生对分式知识重组和思维激活．

教学难点 分式函数图象和性质的探究．

2 教学过程

2.1 设疑自探

2.2 解疑合探

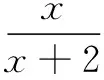
2.3 质疑共探

教学说明整式进阶到分式，多了分母不为0的约束．为了防止学生思维的“滑过”，对分式方程增根有必要使学生数学思考由表及里、由浅入深：一是对问题的正向追问，让学生开展批判性学习，加深对分式增根的原因认识和检验的重要性理解；二是对问题的逆向设计，让学生对分式方程无解有新的认识，这样从基础知识的“点”走向基于知识理解的“线”和“面”，增强了数学思维的广度和深度，从而以深度教学引领学生思维从“理解、应用”进阶到“分析、评价、创造”．

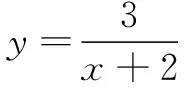
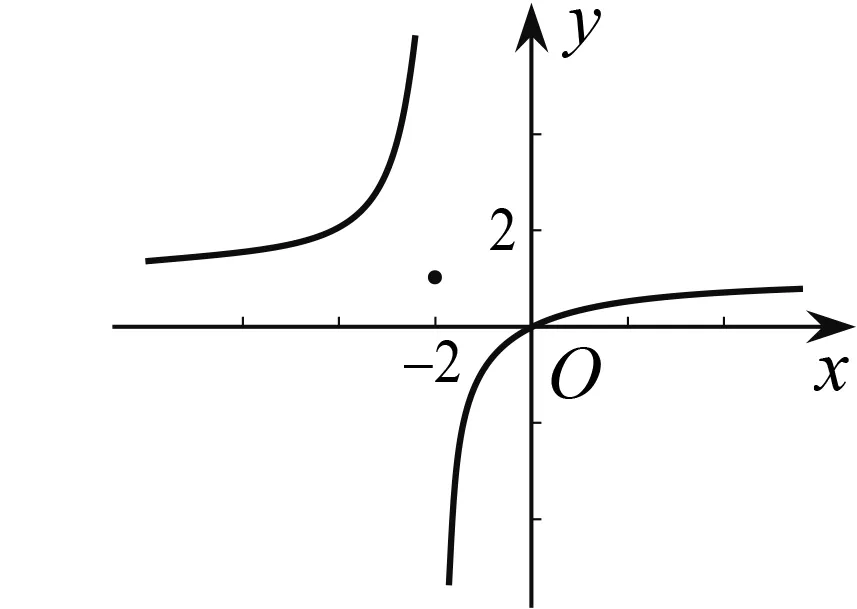
图1

2.4 悬疑再探

活动1 本节课的学习路径是什么？你能用结构图表示吗？(图2)

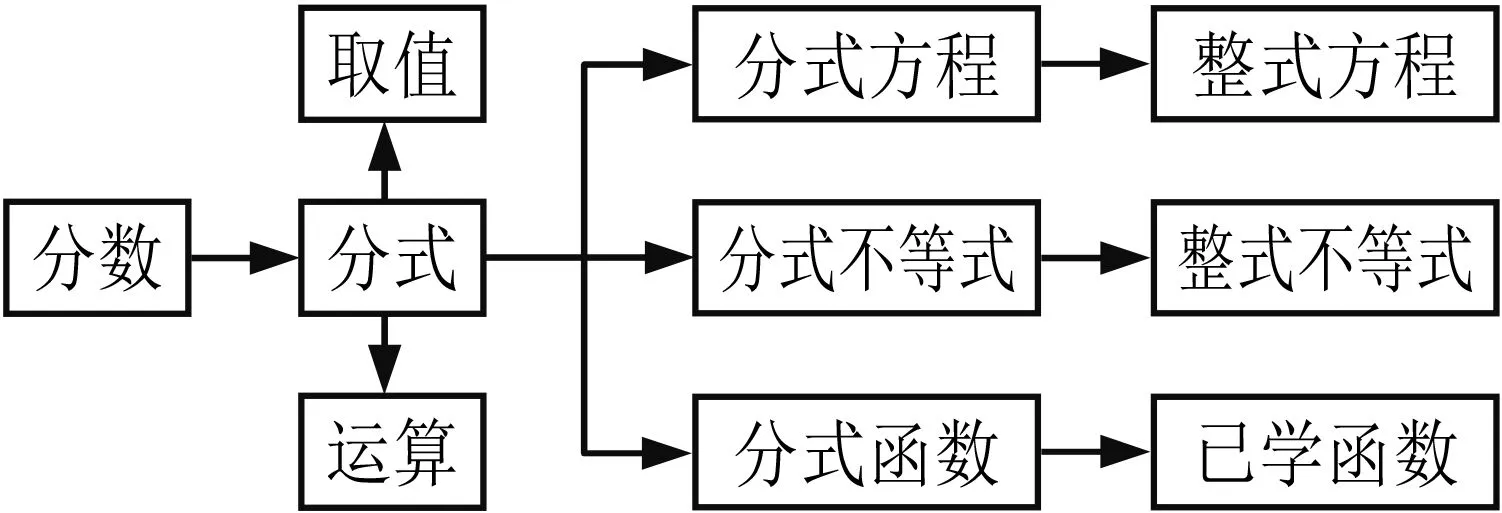
图2

教学说明自我反思是深度学习的一个重要环节，在课后阶段通常应给学生驻足回望的时空，引导学生建构反思．而结构化思考是发展学生高阶思维能力的重要手段，因此教师要善用结构化教学去培养学生的结构化思维．本环节活动能改变以往形式化的小结方法，通过建构反思能直指学生学的设计，打通分式学习脉络，导引学生思维的流向，促进学生积极的学．实现化思考为思维、化经历为经验，使学会学习真正发生，助推学生在学习道路上行稳致远．

教学说明数学是思维的体操．活动2能让学生展开联想，如几何中的线段的比、周长的比、面积的比、锐角三角函数的值等，这样不仅能引导学生主动思考、合理建构、延展思维，还有利于学生在知识重构中获得思维进阶，优化学生的思维品质，实现为理解而教．我们提倡课堂教学真正使学生不仅会“学答”，更能“学问”，做到让学生课始“带着问题走进课堂”，课末“带着问题走出课堂”．最终帮助学生建立自己的数学现实和数学学习的直觉，学会运用数学的思维方式进行思考[1]．

活动3 布置作业(略)．

3 回顾与反思

3.1 设计思路

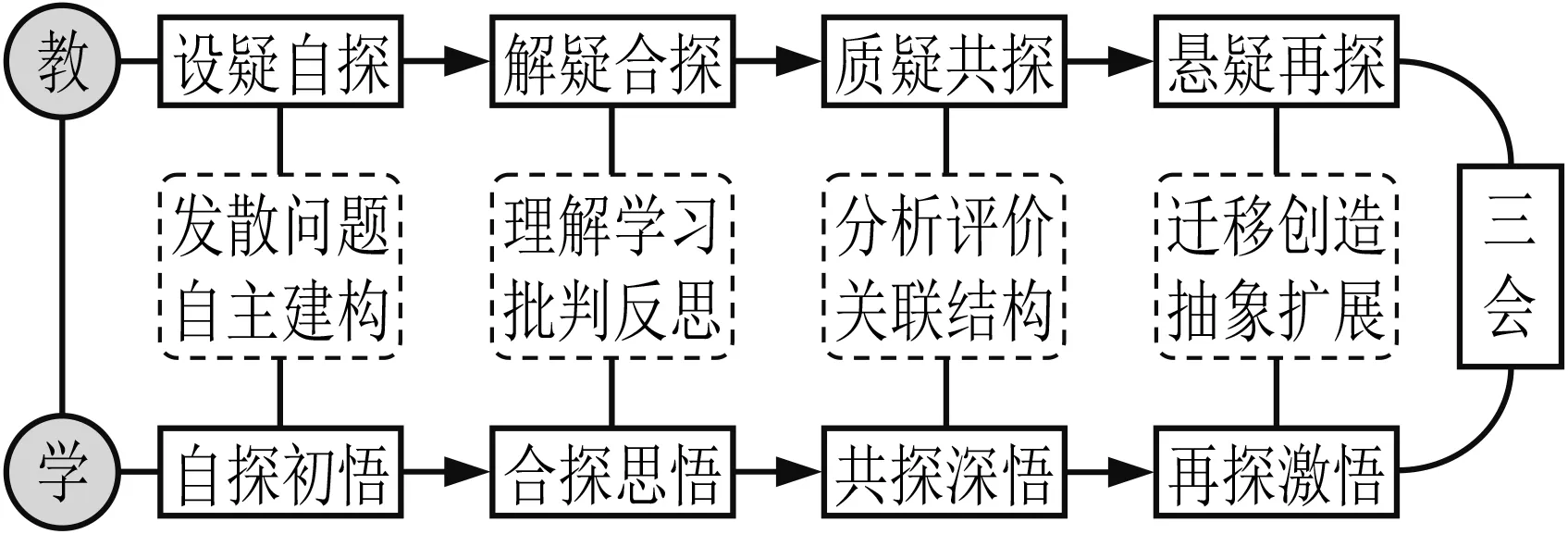
图3

3.2 教学反思

(1)组织探悟活动筑牢思维进阶的落点

教学设计应凸显“让教于学”理念，要树立“以学习者为中心”的数学课堂变革意识，用教学目标的高度去引领课堂教学的广度和深度[3]．而本节课采用从数到式再到关系式的设计思路，在各个教学环节都有相应的思维进阶活动，因此教学目标应有清晰的思维发展目标，在筑牢识记、理解、应用等低阶思维能力基础上，凸显分析、评价和创造等高阶思维认知方式．在自探初悟阶段通过识记、理解等认知方式发展学生可观察的思维结构从单点结构走向多点结构；在合探思悟阶段通过理解、应用等认知方式发展学生可观察的思维结构从多点结构走向关联结构；在共探深悟阶段通过分析、评价等认知方式发展学生可观察的思维结构从关联结构走向抽象扩展结构；在再探激悟阶段通过分析、评价、创造等认知方式发展学生可观察的思维结构走向关联结构和抽象扩展结构．从而让学生在原有低阶思维的基础上开展富有理解性、批判性、迁移性和创造性的深度学习，促进教学改进发生．

(2)整合学习内容联结思维进阶的节点

目前学科教学转型为学科育人，课堂教学走向为思维进阶而教．在初中阶段数学思维主要指运算能力和推理能力．而分式是培养学生运算能力和思维能等学科素养的重要抓手，对其复习应打破知识壁垒，依据课程标准和数学教材，以系统视角进行抽象提炼和归纳总结，采用爬梯式方式促进分式知识系统化、迭代化学习．内容设计首先要选择驱动性问题作为进阶起点．根据知识的逻辑性和思想方法的一致性进行问题链的设计，将散落的知识进行整体设计，以联系的方法看待知识，以期学生在深度学习的过程中有高阶思维参与并形成结构性的知识体系[4]．通过将核心知识问题化，如在分式知识拓展到分式不等式、分式函数上，引导学生多维度、多视角思考问题，做到横向联系、纵向挖掘，并在此过程中体验探究、感悟收获和反思得失．为了使学生学习获得的不仅是点状思维，还有知识以外的深刻经历和系统思维，我们应充分把机会留给学生的“探”，把时间留给学生的“悟”，把精力放在指导学生的“学”，从而为思维进阶提供持续动力．

(3)加强持续评价推动思维进阶的远点

立足于高阶思维能力发展的教学改进，应根据学生的适时反馈，对教学策略和教学内容做相应的调整，教学评价应做到全程化、全面化，以发挥其导航、护航的功能．在思维进阶的起点——自探初悟阶段应加强情感激励性评价，以激活学生思维，促进学生思维展开联系与转化；在思维进阶的关键点——合探启悟和共探深悟中，学生经历知识的应用与分析、思维的抽象与扩展、思想的批判与反思的过程，这时应加强过程性的嵌入式评价，以促进学生从教学的“旁观参加者”变为学习的“主动参与者”；在思维进阶的落点——再探激悟环节中，学生通过有效思辨、合作交流，能力得以进一步提升、思维得到进一步提高，这时应加强跟进式评价，以促进对知识的深层理解、能力的深度迁移与情感的深刻内化，进而从学以致用到学以致学，推动“探悟数学”——“探数学之秘、悟学习之道”走深走远．