“数学文化情境试题”课堂教学实践——以“数学文化之旅——空间图形体积问题”教学为例

陈 振 (江苏省常州高级中学 213003)

数学文化是指数学的思想、精神、语言、方法、观点以及它们的形成和发展，还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动．《普通高中数学课程标准(2017版)》[1]指出：数学文化应融入数学教学活动．教育部考试中心颁布的2017年高考数学考试大纲增加了对“数学文化”的考查，这使得数学文化素养对我们而言愈加重要．为顺应时代要求，努力达成课标要求，笔者尝试进行数学文化情境试题探究，并据此开设了本校的校庆公开课．通过查阅近年来各地高考模考试卷，决定以“空间图形体积问题”这一微切口展开尝试，和学生一起探讨、研究数学文化情境试题．本课题面向高三一轮复习的学生，学生已经具备完整的高中数学知识，且对数学文化试题有了一定的了解．下面将结合本节课教学设计作一些分析与反思．

1 教学设计

1.1 基础巩固——读图

纵观数学的历史，“形”的意识也许跟人类历史一样古老．中国的几何有着悠久的历史，据可靠记载，在中国出土的新石器时代的陶器大多为规则形状，陶器上有各种几何图案，通常还有三个着地点，这些都是几何知识的萌芽(图1)．

图1

设计意图精美图片展示我国古人的几何智慧，激发学生探索几何图形的兴趣．

接着，选取其中的一个紫砂壶为情境作为例1．

例1紫砂壶是中国特有的手工制造陶土工艺品，紫砂壶的壶型众多，经典的有西施壶、掇球壶、石瓢壶、潘壶等．图2给出了一个石瓢壶的相关数据(单位：cm)，则该壶的容量约为( )．

图2

A.100 cm3B.200 cm3

C.300 cm3D.400 cm3

设计意图在呈现问题时，笔者有意将原题中的一关键条件——“壶体近似看成一个圆台”隐去，而这一条件学生是可以通过图形得到的，重点关注读图能力的培养．同时，隐去条件后，本题就是一道有开放性意味的情境问题．学生可以解读成圆台，也可以看成是其他几何体．

真实课堂中有学生将壶体当作圆柱，这当然是不合理的，引导学生再读图去发现，壶长和口径长不同，不符合圆柱的特征．笔者顺势和学生一起复习圆柱、圆锥、圆台的几何特征，巩固立体几何图形基本知识．也有学生将壶体看成是球体的一部分，但在计算容量时学生自然会发现，近似看成球体后，由于球体的半径不明确，体积的求解难以实现，本道例题还是视作圆台更合适．笔者也鼓励学生在课后查阅资料，进一步完善球体计算这一想法，达成自主探究目标．这些都是有意义的课堂生成.通过和学生一起读图分析，向其传递一个信息：重视读图．通过读图，一般可以获得一些有效信息．同时，读图要有问题意识，带着问题阅读图形，将研究图形本身的特征与关注题目要解决的问题有机融合．

补全题目后，引导学生将相关数据与图形结合起来，并在图中标注好，谨防出现数与形不对应．去掉情境，题目为：已知一圆台，上底面半径是3，下底面半径是5，高是4，求壶的容量，即是求圆台的体积．此时学生依然有不同的选择：直接运用圆台的体积公式，或是利用大圆锥减小圆锥．笔者又和学生一起复习基本几何体的体积公式．最后，这道题目还涉及估算，学生若能将π近似为3，计算将得到简化，既节约了时间又提高了正确率．

这道题目由课堂情境导入，自然顺畅产生，文字叙述也简洁凝练．题目虽简单却涉及多个知识点，涵盖了立体图形的几何特征、体积公式等解决“空间图形体积问题”的必备知识．同时初步渗透读图、作图、用图的思想，培养去情境化、建立模型的意识．能读图，依据问题意识读出有效的图形，是问题解决的前提．

1.2 能力提升——作图

我们的古人在生产生活实践中也产生了很多图形问题，发展出很多求解几何体体积的方法．《九章算术》是我国古代的数学巨著，对于中国和东方数学，大体相当于《几何原本》对于希腊和欧洲数学．其卷第五“商功”章主要讨论空间几何体体积求解问题，从中选择一道作为例2让学生都来解一解．

例2《九章算术》是我国古代的数学巨著，其卷第五“商功”章有如下的问题：“今有刍甍(chú ménɡ)，下广三丈，袤四丈，上袤二丈，无广，高一丈．问积几何？”意为：“今有底面为矩形的屋脊形状的多面体(图3)，下底面宽3丈，长4丈，上棱2丈．上棱平行于下底面且与下底面的距离为1丈”，则它的体积是立方丈．

图3

设计意图例2依然是一道具体情境下的空间几何图形的体积问题．呈现题目时，也刻意隐藏了原题中的数学图形，而换成了一张生活实景图．需要学生依据刚刚的解题经验，通过阅读题目，自己作图，抽象出相应的几何体．

笔者通过课堂观察，发现学生基本都能读懂题意并作出图形．但作图依然存在两类问题：一是虚实线不分，导致空间图形立体感不强；二是方位不对，空间的点线面位置关系不清晰．这些图形正确却不很合理，不符合立体图形的审美要求，不利于解题．在平面中展示立体图形，是一个难点，需引导学生慢慢体会与感悟．

此时，我们已经可以将这道问题的情境过滤，用数学语言描述问题．

例2今有底面为矩形的屋脊形状的多面体(图4)，下底面宽AD=3丈，长AB=4丈，上棱EF=2丈，EF∥平面ABCD．EF与平面ABCD的距离为1丈，则它的体积是立方丈．

图4

笔者追问：“这是什么几何体呢？”引导学生发现这是一个一般的空间五面体，并不是我们熟悉的柱锥台，不能直接运用体积公式．那怎么办呢？学生大多会想到割补的思想．笔者适时给予鼓励：这和我们古代数学家的想法是一致的！顺势介绍《九章算术注》，刘徽在书中全面论证了诸多几何体体积公式，并发展了出入相补原理、截面积原理、齐同原理等．其中出入相补原理是：一个立体图形被分割成若干部分后，体积的总和保持不变．佐证学生的想法，鼓励学生进一步探究到底．

利用割补的方法，大多数学生都能够顺利解决问题．但也有人在解题时直接将EF摆在中间的位置，默认几何体两侧面对称，简化了运算，得到的结果也是一样的．此时，课堂生成了新问题：“本道题将几何体特殊化求体积，可以吗？”学生会有不同的意见与想法，待他们充分表达后，笔者展示事先准备好的GGB动画，通过直观观察发现，改变EF位置，几何体在所有等高处的截面面积保持不变．利用祖暅原理，即可确定体积不发生改变．因此，本题将几何体特殊化来求体积是可行的．

顺势向学生介绍祖暅原理[2]．祖暅用这一方法，证明了球体体积的计算问题．我国古代数学家在极限思想的运用上远远超过了同期其他国家的同类思想，达到了文艺复兴前世界数学界的最高峰．民族自豪感油然而生！

这道例题由《九章算术》而来，富含文化底蕴．其难度较例1有所提升，学生要通过读题准确作出图形，求解体积的方法也不再是简单地套用公式，强化渗透读图、作图、用图的思想，培养去情境化、建立模型的意识．会作图，把握重要因素，准确作出图形，是问题解决的关键．

1.3 知识迁移——用图

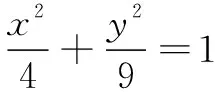
图5 图6 图7

A.4π B.8π C.16π D.20π

设计意图以祖暅原理为情境背景的题目有不少，笔者选择的这道例题需要学生先类比作出与要求几何体等体积的基本几何体再进行体积求解．这是一个难点，需要学生真正理解祖暅原理，并读懂、用好题目中的橄榄状的几何体．本题有一定思维度，为了让学生真正掌握祖暅原理的本质而非限于解决题目本身，鼓励学生进行小组讨论并将讨论结果在班级展示．

这道例题不再是考查学生用已经掌握的基本方法去求空间几何体体积，而是在创设的情境中给学生提供思路，让学生直接应用到体积的求解中，对思维的要求是更上一个层次的．因此，笔者鼓励学生合作学习，通过组内讨论和小组分享，让所有学生参与其中，集众人智慧解决问题．这既不会让部分学生望“题”兴叹，又达到了思维训练的难度．学生的表现也很亮眼，不仅顺利建立了等体积的模型，而且通过计算论证了截面面积保持相等，严谨证实了模型的合理性，令人惊喜.

这道例题的情境既是背景又是工具．祖暅原理是教材中的阅读材料，但绝非晦涩难懂，放在情境中，既达到了深层次的考查目标也不会超纲．同时，进一步渗透读图、作图、用图的思想，培养去情境化、建立模型的意识．会用图，抓住关键特征用好图形，是问题解决的难点．

2 教学反思

近几年高考，以数学文化为背景的空间几何体体积问题层出不穷，让人耳目一新，同时，它也让我们受困于背景陌生，阅读受阻，思路无法打开．为了尝试改变这一局面，笔者设计了这节课，选用的大体是两类情境：作为素材背景显性呈现的情境，主要是例1、例2，例1复习了空间几何体基本几何特征、基础体积公式，例2渗透了割补的基本方法；以及作为思想方法隐形呈现的情境，主要是例3，运用“文化”蕴含的数学思想和数学方法进行数学解题，将祖暅原理应用于体积求解．力求为学生渗透读图、作图、用图的思想，培养去情境化、建立模型的意识．

本节课通过对一些高考、模考试题的剖析求解，并穿插相关数学文化的介绍，提升学生阅读理解的信心，增加学生对数学文化的认识，加深对数学文化的理解，落实四基四能．将数学文化融入教学，还有利于激发学生的数学学习兴趣，有利于学生进一步理解数学，有利于开拓学生视野，提升数学学科核心素养．