基于传统文化 构建问题情境 走向自明学习
——以苏科版八年级“函数”为例*
2023-03-01胡永强江苏省苏州市阳山实验初级中学校215151
胡永强 (江苏省苏州市阳山实验初级中学校 215151)
1 引言
函数概念是从常量数学向变量数学过渡的重要节点.初中生首次接触函数概念,对它的理解存在较大困难.因此,如何恰当设计函数概念教学,促进学生深入理解函数概念显得尤为重要.学生在学习某个新的概念时,教师应当给学生提供与学生的认知程度相符合的情境,启发、引导和帮助学生逐步独立完成新概念的学习,提升学生学习新知识的能力水平[1].
苏科版数学教材借助高铁匀速行驶情境引出常量、变量,进而通过水库中水位与蓄水量、用火柴棒搭小鱼中火柴棒根数与小鱼条数、水滴激起的圆形波纹面积与半径三个情境引出两个变量间的关系,最终概括出函数的变量对应说定义.然而,教材中给出的情境之间缺少联系,这一方面增加了学生的认知负荷,另一方面也难以帮助学生形成系统的认知经验.
现有的教学设计中大多按照教材内容进行组织,给出较为丰富但没有关联的情境以引出函数定义,很少设计出有联系的情境,将中华优秀传统文化融入函数概念教学以及在函数定义教学中渗透学科德育[2-4].中华优秀传统文化绵延数千年从未中断,其中蕴含丰富的可供选用的教学素材,有待教师发掘并应用于教学.基于此,笔者从中华优秀传统文化中撷取部分素材,设计一节函数概念课并付诸实践,促使学生自己理解并建构函数概念、渗透学科德育并朝着自明的目标迈进.
2 史料分析
变化思想在中国古已有之,比如《易经》中的“易”就有变化的意思,主张世界本质上是不断变化的,人必须通晓世界的变化,才能认识世界[5].
唐朝窦叔蒙撰写的《海涛志》中设计了一个具有纵横两轴的坐标系统,用以推算并记录一个农历月份的高低潮时(如图1),这是世界上最早的高低潮时推算图,其间蕴含着函数思想[6].

图1 唐·窦叔蒙高低潮时推算图
现代意义上的函数定义起源于西方.17世纪德国数学家莱布尼茨首创function一词用来表示函数.19世纪我国清朝数学家李善兰与英国传教士韦列亚力合作翻译英国数学家德·摩根和美国数学家伊莱亚斯·罗密士的数学著作时将function一词翻译为函数,将德·摩根《代数学》一书中的函数定义翻译为:凡式中函天,为天之函数.将伊莱亚斯·罗密士的《代微积拾级》中的函数定义翻译为:凡此变数中函彼变数,则为彼之函数.“函”与“含”同义,有包含的意思[7].
本节课采用多种数学史运用方式将以上历史素材融入函数概念教学.基于唐朝窦叔蒙《海涛志》这一历史素材,设计3个有代表性的情境,让学生经历函数定义的探索与提炼过程,属于顺应式运用.在新课伊始,借助《易经》引出研究变化现象,在提炼出函数定义后借助微视频向学生介绍函数定义的相关历史演进过程,提升学生的文化涵养,属于附加式和复制式运用.
3 教学过程
基于对教材和历史的分析,结合学生的认知水平,将本节课的教学目标确定如下:(1)通过潮时与日期情境理解常量与变量的概念;(2)通过潮时与日期、潮位与时间和月最高潮高与月份3个情境探索函数概念;(3)了解函数概念发展历程,感悟古人智慧,培养理性精神和积极的数学信念.本节课的教学重点是探究并理解函数的概念,教学难点是理解函数概念中的两个变量间的对应关系.主要设计与实施教学环节如下.
3.1 创设函数情境
情境1 潮时与日期的关系.
师:同学们,我们生活在一个变化的世界中.研究变化问题古已有之,据史书记载,周文王姬昌在伏羲氏创立的八卦基础上,写成《易经》一书.此书中的易有变化的意思,主张世界本质上是不断变化的,人必须通晓世界的变化,才能认识世界,推动世界向前发展.
蔚蓝的大海是生命的摇篮,其间包含许多变化的现象.例如潮水每天上涨又退去,其中蕴含着一些规律,研究潮水涨落的学问称为潮汐学,其中的潮汐预报对生活在海边的人们非常重要,尤其是对船只的出海与入港有着十分重要的意义.
下面我们一起来了解一下潮汐的相关知识.
师:窦同学从小就对潮汐十分感兴趣,他每天都会到海边观察、记录、研究潮汐.经过一段时间的研究,他发现每天涨潮的时间比前一天推迟48 min.在这个过程中哪些量没有变化?哪些量不断变化?
生:每天涨潮比前一天推迟的时间保持不变,日期和涨潮时间不断变化.
师:在这一变化过程中,相邻两天涨潮时间的差是保持不变的量,叫做常量,日期和涨潮时间是可以取不同数值的量,叫做变量.(板书:常量、变量)
师:根据上述规律,假设初一的涨潮时间为 0:48,那么初二的涨潮时间是多少?
生:初二的涨潮时间为1:36.
师:日期为n的涨潮时间如何表示呢?
(学生陷入沉思)
师:如果设日期为x,涨潮时间为y,为了便于计算,现将时间先按十进制计算,你能用一个式子表示y与x之间的关系吗?
生:y=48x.
师:以上我们发现,一个月中涨潮的时间随日期的变化而变化,随日期的确定而确定.(板书:x变→y变;x定→y定)下面我们再来研究一天中涨落的水位(也称潮位)情况.
情境2 潮位与时间的关系.
师:图2是从某潮汐网站上下载的我国连云港2022年11月15日潮汐表.观察图2,你有哪些发现?

图2 连云港潮汐图
生:时间变化,潮位变化.
生:时间确定,潮位也确定.
生:一个时间对应一个潮位.
师:研究完一个月中的涨潮时间和一天中的潮高问题,下面我们再来研究一年中每个月的最高潮位问题.
情境3 最高潮高与月份的关系.
师:表1是某海港12个月的最高潮高表,观察此表你有哪些发现?

表1 某海港12个月的最高潮高
生:月份变化,最高潮高也在变化.
生:月份确定,最高潮高也确定.
生:对于月份的每一个值,最高潮高都有唯一的值与它对应.
设计意图本节课是引导学生从常量数学学习向变量数学学习过渡的关键一课.通过师生谈话引出研究变化问题这一主题,随后简要介绍《易经》,让学生了解我国古人早已对变化的问题有所研究,提升人文修养和文化自信.以海潮为背景设计的三个情境,帮助学生获取函数的解析法、图象法和表格法三种表达形式,以此引导学生总结并发现常量及变量的概念,借助问题支架探索两个变量之间的关系,为后面提炼函数定义打下坚实的基础.
3.2 提炼函数定义
师:上述3个情境有什么共同特征?
生:都是变化的过程;都有两个变量;当一个变量确定时,另一个变量也随之确定.
师:一个变量取某一值时,另一个变量有几个值与它对应?
生:另一变量有唯一的值与它对应.
师:请你用一段话描述上述共同特征.
几名学生接力回答,不断补充完善.
教师结合学生回答总结并板书函数定义:一般地,在一个变化过程中的两个变量x和y,如果对于x的每一个值,y都有唯一的值与它对应,那么我们称y是x的函数(function),x是自变量.
师:你认为函数定义中有哪几个地方比较重要?
生:变化过程.
生:两个变量;对于x和y;对于x的每一个值,y都有唯一的值与它对应.
师:很好.(结合学生回答用彩色粉笔对定义中的重点内容作出标注)
师:请结合上述3个情境说一说谁是谁的函数,谁是自变量?
生:涨潮时间是日期的函数,日期是自变量;潮位是时间的函数,时间是自变量;最高潮高是月份的函数,月份是自变量.
师:历史上函数概念的发展经历了漫长的过程,下面我们通过一段微视频来了解一下吧.(播放函数历史微视频)
我国古代已经有了函数思想,并且运用此思想观察研究.唐朝时期民间科学家窦叔蒙从小对海洋潮汐很感兴趣,连续观察研究发现涨潮时间随着日期的变化而变化.他将自己的研究成果写成《海涛志》一书,在书中,他设计了一个具有纵横两轴的坐标系统,推算并记录一个农历月的高低潮时,这是世界上最早的海洋高低潮时预报法,其间蕴含着函数思想,比欧洲最早的“伦敦桥涨潮时间表”还早450年.现代函数定义起源于西方.17世纪德国数学家莱布尼茨首创function一词表示函数.在我国,清代数学家李善兰(1811—1882年)在翻译西方数学著作时,把function译成“函数”,并沿用至今,这里“函”与“含”同义,有包含的意思.
师:视频中介绍,函数一词是我国清朝数学家李善兰在翻译西方数学著作时给出的,他所翻译的美国数学家罗密士的《代微积拾级》一书中的函数定义是:“凡此变数中函彼变数,则此为彼之函数.”这里的变数就是变量[7].
师:请以y=48x为例,解释一下李善兰所翻译的函数定义.
生:变量y是48x,其中含有变量x,所以称变量y是变量x的函数.
师:潮位和时间以及最高潮高与月份这两个函数关系可以用李善兰翻译的函数定义解释吗?为什么?
生:不可以.因为它们不能写出关系式.
师:请你对比现在给出的函数定义与李善兰翻译的函数定义,思考二者有何区别?
生:李善兰翻译的函数定义只限于两个变量能够写出关系式的类型,现在给出的函数定义没有这个限制,只要满足变量x的每一个值,y都有唯一的值与它对应,就可以称y是x的函数.
师:很好.我们现在给出的函数定义与李善兰翻译的函数定义相比适用范围更广.假如你不知道函数名称,你打算给它起个什么名字呢?请写下来.
生:对数、应数、关数、联数.
师:大家给出的名称都有道理.对此你有何感想?
生:数学不是僵化的,是不断发展变化的.
师:结合上述3个情境说一说函数有哪些表现形式?
生:关系式、图形、表格.
设计意图遵循概念教学的APOS理论,帮助学生逐步建构函数定义:引导学生寻找前面3个情境的共同特征—提炼本质特征—概括得出函数定义—检验3个情境是否符合定义.同时,通过微视频向学生介绍相关中华优秀传统文化,帮助学生全面了解函数发展历史,感悟古人的智慧,增强文化自信,发展正确的数学观.
3.3 感受函数应用
例1如图3,把水滴激起的波纹看成是一个不断向外扩展的圆.这里有哪些变量?请找出它们之间的函数关系,并说明理由.

图3
例2某水库水位的高低与相应的蓄水量如 表2所示.

表2 某水库的水位与蓄水量
蓄水量是水位的函数吗?为什么?
例3用一根长2 m的铁丝围成一个长方形.
(1)当长方形的宽为0.1 m,长为多少?
(2)当长方形的宽为0.2 m,长为多少?
(3)这个长方形的长是宽的函数吗?为什么?
设计意图借助教材中的素材编制3道例题,帮助学生进一步理解函数定义.例1是一道开放性问题,只要学生说得有道理即可;例2与表格形式相对应;例3可以写出关系式,与关系式形式相对应.
3.4 编制函数问题
师:请你编写一个包含函数关系的实际问题,让你的同伴找出其中的函数关系,并指出常量和变量.(学生独立编题—两人一组相互交流—教师选择学生展示作品)按照作品类型梳理如下:
类型1y=kx模型.(图4)

图4
类型2y=kx+b模型.(图5)

图5
类型3 其他模型.(图6)

图6
设计意图课堂留白,让学习真正发生,体现学生的主体地位,帮助学生深入理解函数定义,激发学习数学的兴趣,提升数学核心素养.
3.5 巩固函数知识
(1)“沙漏”是我国古代一种计时仪器,它根据一个容器里的沙漏到另一个容器中的数量来计量时间.请找出这个变化过程中的变量,说一说谁是谁的函数,并说明理由.
(2)数值转换机.
教学说明:以动画形式呈现,输入一个实数x,输出一个实数y(图7).教师演示两组,再选几位学生实际操作.
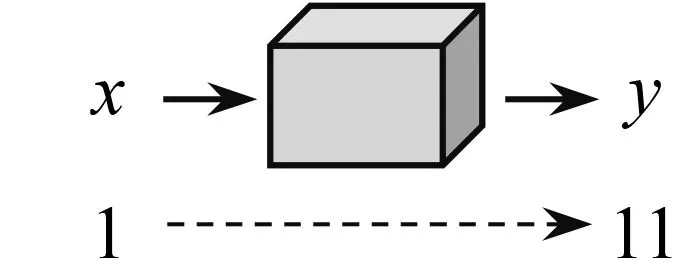
图7
师:数值转换机中的y是x的函数吗?为什么?
生:y是x的函数,因为它符合函数定义.
(3)请结合图8,选几个x的值输入,按照程序计算出相应y的值.思考:y是x的函数吗?为什么?
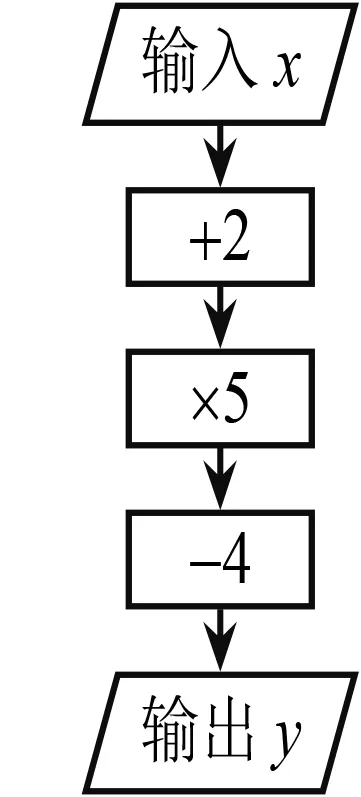
图8
生:(选值计算后)y是x的函数,因为它符合函数定义.
师:将运算程序图与数值转换机相对照,你有什么发现?
生:我知道其中的秘密了,数值转换机是按照这个运算程序图设计的.
师:太棒了!由此你有什么感想?
生:数学太神奇了.
设计意图巩固理解函数定义,体会数学的神奇之处,激发兴趣.
3.6 总结函数内容
引导学生从基础知识、思想方法、情感态度三个维度对本课内容进行小结.作业包括教材习题和寻找生活中变化的问题,说出其中的常量与变量,判断变量之间是否存在函数关系.
设计意图梳理、回顾本课所学内容,建构知识体系,实现德育之效.
4 学生反馈
在实施本课之前和之后分别对42名学生进行了前测和后测,对调查结果加以整理和分析发现以下结论:
对于本节课与函数相关的历史素材的价值,95%的学生表示窦叔蒙潜心研究海洋潮汐现象,创造二维坐标系统揭示涨潮规律的故事让自己更深刻地理解函数定义;90%的学生提到李善兰首次翻译函数的定义并给出函数名称,加深自己对函数的印象.
对窦叔蒙的故事的启示,多数学生写道:生活中到处都有函数问题,我们要热爱生活、善于观察、勇于探究、深入钻研、持之以恒,研究问题要有科学严谨的态度、要勇于创新,数学很有用.
对本节课印象最深的环节,60%的学生表示印象最深的是自主编题环节,他们认为这个环节调动学习气氛,让同学们说起来,加深自己对函数定义理解的同时感受到学习函数的快乐,倾听同伴问题时让自己受益很多.31%的学生表示对介绍函数历史的微视频印象深刻,特别是我国唐朝窦叔蒙借助二维坐标系统进行潮汐预报比西方早400多年,这是十分了不起的成就.
以上我们可以看到,本课融入的几则数学史料深受学生喜爱,对学生起到了多方面的积极影响,他们借此深刻理解知识的同时对数学的兴趣变得更加浓厚,深刻感受到中华优秀传统文化的魅力.课堂编题活动受到绝大多数学生的欢迎,使他们学会思考与倾听、学会交流与表达.
5 教学启示
5.1 基于传统文化,设计教学情境
《义务教育数学课程标准(2022年版)》(下称《标准2022》)在课程实施的教学建议中提出:注重情境素材的育人功能,如体现中国数学家贡献的素材,帮助学生了解和领悟中华民族独特的数学智慧,增强文化自信和民族自豪感.[8]本节课以我国唐朝时期潮汐学家窦叔蒙使用二维坐标系统预测潮汐这一历史素材为背景,创设“潮时与日期”“潮高与时间”“最高潮高与月份”三个情境,帮助学生从“解析式”“图象”“表格”三个维度探究函数定义.
5.2 构建问题之链,走向概念自明
《标准2022》指出,教师应注重问题提出对学生主动参与教学活动的促进作用,设计合理问题,激发学生学习动机,促进学生积极探究[8].本课以潮汐为背景设计了三个问题情境,构建探索函数概念的问题链,引导学生积极思考、主动探索,研究函数的三种不同表达形式,在此基础上顺利提炼概括出函数的定义,进而返回检验三个情境是否符合函数定义,最终达到对函数定义的自明之效.此外需要指出的是本课所构建的问题链对后续学习也将产生积极影响,潮汐情境为高中学习周期函数打下认知基础,函数机为高中阶段的函数集合定义奠定基础.
5.3 创设问题之白,提升核心素养
课堂留白为学生发现和提出、分析和解决问题创造了条件,能有效提高学生的课堂参与度,实现深度学习,促进学生核心素养的提升[9].本课设计让学生自主编题并与同伴交流环节,属于问题之白.此环节学生高度参与,兴趣高涨,相互启发.从课堂展示中我们可以发现,编题活动很好地促进了学生对函数定义及本质的理解,课后问卷也显示学生对此环节非常喜爱.同时,编题活动也很好地培养了学生的数学抽象、逻辑推理、沟通交流和主动倾听等能力,让学生抛开自我中心,懂得换位思考、尊重他人.
5.4 融入信息技术,渗透学科德育
信息技术融入数学教学是新课程改革倡导的理念之一,中华优秀传统文化与信息技术相结合融入课堂教学有助于开阔学生的视野,落实学科德育任务.在教学过程中,可以借助浏览网站、观看微视频等信息技术手段呈现中华优秀传统文化的相关素材,从而有效渗透学科德育.本课借助微视频向学生介绍窦叔蒙研究潮汐及李善兰翻译函数等中华优秀传统文化素材,帮助学生体会到做学问必须具备认真观察、潜心钻研、持之以恒、勇于创新等优良品质,感悟到数学是不断发展变化的,同时真切体悟到中华优秀传统文化的魅力.此外,以小程序形式呈现的数值转换机,在帮助学生深刻理解函数定义的同时也让学生感受到数学的神奇,提高学生对数学学习的兴趣,促进学生思考其背后的原理,培养理性精神.
(注:在本课设计与本文写作过程中,苏州大学数学科学学院沈中宇老师给予很多帮助,在此表示衷心感谢!)
