基于工业机器人的图像引导圆孔定位方法

马超，曹国华，2，丁红昌，2

(1.长春理工大学机电工程学院，吉林长春 130022；2.长春理工大学重庆研究院，重庆 401135)

0 前言

近年来，随着工业自动化程度的不断加深，通过工业机器人进行自动化装配已经逐渐代替人工装配。而轴孔装配在自动化装配中占有主要的地位，由于轴孔装配要求的精度较高，所以对待装配工件上的圆孔参数测量与定位在轴孔装配中是尤为重要的一步。

相比于传统的检测方法，基于视觉的孔测量与定位方法具有操作灵活、低成本、无需接触工件、不损伤工件等优点。LYU等[1]将一维单应性应用于圆姿态测量，该方法可以将线性求解结果优化，但此方法对噪声的鲁棒性不佳，所以不能将此方法应用于实际复杂的工作场景中。LI等[2]通过单目视觉测量系统测量孔位姿，但是单目视觉测量系统对于深度的测量稳定性与精度均不是很理想。李振[3]利用双目立体视觉、三维重建等方法对孔位姿进行测量，但是在椭圆检测时若获得的圆孔轮廓为不完整轮廓，该算法就会失效。WU等[4]针对金属零件弱纹理的特点，采用了锥退化的方法来测量圆形工件位姿，最后实现六自由度机器人对工件实施抓取，但是应用该方法若光照与图像分辨率选择不当，则会导致椭圆拟合时产生一定的误差，并且无法将其应用到高精度的轴孔装配上。LIU等[5]针对三维柔性视觉检测系统，提出了一种基于结构光视觉传感器的两步空间圆定位方法，但该方法仅获得圆的中心位置，无法确定方向。XIA 等[6]提取孔边缘并利用其边缘点对圆孔进行三维重建，得到圆孔位姿。LIN等[7]提出一种基于视觉的位姿估计方法定位工业机器人工作空间中轴孔。JIANG 等[8]采用双目立体视觉对空间孔三维重建，实现机器人轴孔装配自动化。KORTA等[9]使用OpenCV库搭建了工业机器人的电路装配视觉系统。综上所述，基于立体视觉的孔位姿与法向检测虽然取得了一定的成就，但是针对金属弱纹理工件匹配点稀疏的情况与在边缘残缺情况下检测椭圆时算法的鲁棒性仍然有待提升。

本文作者将以弱纹理的金属孔板工件为研究对象，基于工业六轴机器人，针对上述问题，提出一种在立体视觉极线约束下的图像引导孔位姿与法向的检测方法。首先对两幅图像进行椭圆轮廓检测，然后利用极线约束找到两幅图像中对应的轮廓匹配点，得到视差关系，最后进行三维重建。

1 检测系统原理与方法

此检测系统在采集完图像后，首先通过双目标定得到的相机参数对双目图像进行立体校正，然后通过文中所提出的基于弧段的椭圆检测算法提取圆孔边缘轮廓，接着通过SURF+RANSAC的算法对双目图像粗匹配，得到双目图像的基础矩阵，进一步通过极线约束的精立体匹配获得精准的视差信息，最后根据双目三角几何原理，进行三维重建，计算得到孔工件位姿。具体检测流程如图1所示。

图1 圆孔位姿检测工作流程

1.1 标定与校正

由于相机在成像过程中，会出现相机光轴不在图像的中心和相机在X、Y方向的缩小系数无法保持一致的问题，故需对相机进行标定，得到相机的内参数与畸变系数来对图像校正。另一方面，文中是通过平行移动机械臂带着单目工业相机获取双目图像，由于机械臂重复定位精度有限，所以需要对双目图像进行立体标定，得到外参数来得到精确的极线距离，并且还可以用得到的外参对双目图像进行立体校正，使得双目图像的对应点在同一水平线上，即2个像平面完全对准，以保证后续处理图像得到的视差信息更加准确。

1.2 基于弧段的孔轮廓图像提取

因为图像在稳定光照环境下采集，所以在提取图像边缘轮廓前仅需要采用高斯滤波对图像中的高斯噪声进行滤除即可。之后，利用由Qtsu改进的自适应阈值Canny算子获取图像中的边缘点。并且，在边缘检测过程中可以得到边缘点水平方向梯度值Gx与垂直方向的梯度值Gy，边缘点的坐标(x，y)。将所有边缘点都定义为Pi=(xi，yi，θi)，i=1，2，…，n。并且将边缘点按照式(1)进行分类，同时剔除Gx=0或Gy=0的边缘点。

(1)

然后通过搜索在边缘点Pi的八邻域中是否存在与其同类别的边缘点Pi+1，直到出现不同类别的边缘点或者边缘点邻域内不存在其他边缘点时结束搜索，形成弧段ζ并对弧段进行去伪。弧段提取流程如图2所示。

图2 弧段提取流程Fig.2 Arc segment extraction process

其中图2中的弧段α去伪方法为：通过计算弧段上边缘点的弓弦比σ，若弧段α上存在弓弦比σ大于设定阈值T的边缘点时，保留该弧段，否则当作伪弧段剔除。图3所示为弧段α上边缘点的弓弦比示意。

图3 弧α弓弦比示意Fig.3 Arc α schematic of bowstring ratio

若弧段α上存在一边缘点为Pi(x0,y0)，弧段两端点为L(x1,y1)、R(x2,y2)，则边缘点Pi处的弓弦比σ可由式(2)计算得出。通过理论分析与实验检测，文中设定弓弦比阈值为0.125。

(2)

(3)

在得到Ⅰ、Ⅱ、Ⅲ、Ⅳ 4种类别的弧段后，通过式(4)可得到椭圆轮廓的弧段三元组。

(4)

其中：ζa、ζb、ζc表示3条不同的弧段；Ⅰ、Ⅱ、Ⅲ、Ⅳ为弧段分类中的4种类别。椭圆平行弦中线定理：椭圆平行弦的中点共线，且该线经过椭圆中心。如图4所示：在2条弧段上做2组平行弦，将2组平行弦中点连接成2条直线，2条直线相交点即为椭圆中心。通过理论分析与实验测试，设定2条弧段之间的平行弦数量阈值应不少于16。

图4 平行弦定理求椭圆中心示意

通过上述过程已经得到椭圆的中心坐标(Ox，Oy)，还剩下椭圆长轴a、短轴b、倾斜角θ3个参数。因为椭圆中心在长轴所在的直线上，设长轴的斜率为ka，根据式(5)便可以得出其直线方程：

kaX-Y+(Oy-kaOx)=0

(5)

若在弧段上存在点P(x0，y0)，则点P到长轴所在直线的距离d可由式(6)计算得出：

(6)

根据椭圆相关几何知识可知，椭圆的长轴将会平分与其垂直的弦。通过式(6)可以得到弦两端点到长轴的距离，以此判断该弦是否被长轴平分。若存在多条这样的弦，则该假设的长轴斜率正确，否则需换一个新的斜率重复上述过程。

在确定长轴的斜率后，也就确定了椭圆的倾斜角θ，并且还可以通过kakb=-1计算得出短轴b的斜率kb。

在得知上述参数后，在长轴上以椭圆中心点为分界线，在中心点两侧选取焦点F1、F2。再任取弧段上的一点M，则根据式(7)即可得到半长轴α与半短轴β的长度：

(7)

式中：c为椭圆的焦距。

1.3 基于极线约束的孔轮廓点匹配

由于银白色金属工件存在弱纹理甚至无纹理的情况，这就导致了若使用传统的SURF与RANSAC等算法进行立体匹配时，会出现匹配点稀疏、缺失重要特征点视差信息等问题。为了解决这种现象，文中将采用基于极线约束的立体匹配方法来解决以上述问题。基于极线约束的立体匹配示意如图5所示。

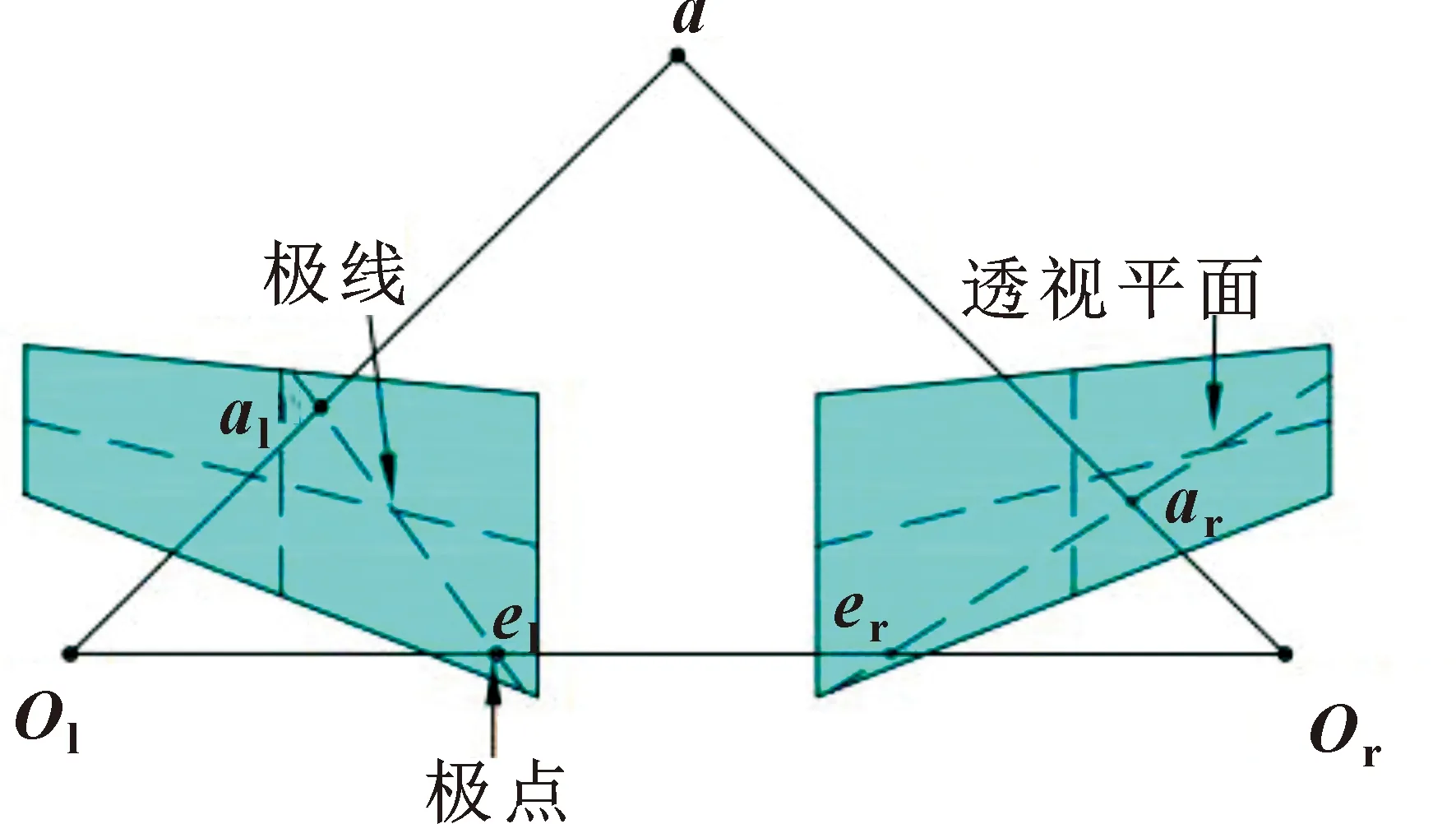
图5 基于极线约束的立体匹配示意

如图5所示，点a为空间中的某一点，点Ol与点Or分别是左右图像的投影中心，二者之间的连线被称为基线，平面aOlOr为极平面。点el与点er分别被称为左极点与右极点，点al与点ar分别是空间点在左右投影平面上的投影点，而左投影点al与左极点el的连线叫做左极线，右投影点ar与右极点er的连线叫做右极线。基于极线约束立体匹配，就是将左右两幅图像上的投影点与极线的关系一一对应，将匹配点的匹配维度从二维平面搜索转化为一维极线搜索上。这样不仅能很好地克服弱纹理工件的匹配精度问题，还可以大幅提升匹配速度。

在进行基于极线约束的立体精匹配前，还需要求解出双目图像的基本矩阵。虽然通过SURF+RANSAC算法得到的双目图像匹配点比较稀疏，但是却可以通过这些匹配点得到较为准确的基本矩阵。然后再结合第1.2节中提取到的圆孔边缘轮廓点的坐标信息，通过极线约束求得两幅图像中的同名点坐标。方法如下：

若已知左图像上的一点D1，则D1对应的右图像上的极线L2可由式(8)来表示：

L2=F·D1

(8)

同理，若已知右图像上一点E1，则E1在左图像中对应的极线L1可由式(9)表示：

L1=FT·E1

(9)

同时还可以得到左右图像上任意对应匹配点之间的转换关系如式(10)所示：

(10)

其中每一条极线Li都是由(a,b,c)3个参数描述的，极线可以表示成式(11)的形式：

ax+by+c=0

(11)

根据左图像中的一点P1求解出右图像中对应的极线后，由于点P1与在右图像中的同名点P2的纵坐标是相同的，所以只需要通过式(9)即可得到同名点P2的横坐标。

综上所述，在得到左图像或右图像的椭圆轮廓上任意一点时，都可以通过上述的方法求得在对应图像上的精确匹配点，获得精准的视差信息。

1.4 孔轮廓三维重建与位姿计算

在得到精准的视差信息后，便可以运用双目视觉模型中的三角几何关系进行三维重建。平行双目视觉模型如图6所示。

图6 平行双目视觉模型Fig.6 Parallel binocular vision model

在图6中点P(xc，yc，zc)为一三维空间点。左右两幅图像分别为机械手臂带着单目手眼相机经过水平移动获取，(xleft,yleft)与(xright,yright)为空间点P在左右图像上的投影坐标，yleft=yright=y，f为焦距,相机主点的像素坐标为(x0，y0)，B为基线长度，视差为：Ddisparity=xleft-xright。根据式(12)可计算出空间点P在相机坐标系下的三维坐标为

(12)

如图7所示，在得到椭圆边缘上若干边缘点三维坐标后，设3个边缘点三维坐标为A(x0,y0,z0)、B(x1,y1,z1)、C(x2,y2,z2)。则向量AB=(x1-x0,y1-y0,z1-z0)=(x3,y3,z3)，向量AC=(x2-x0,y2-y0,z2-z0)=(x4,y4,z4)。可以计算得出圆孔所在平面的法向量为：AB×AC=(y3z4-y4z3)i-(x3z4-x4z3)j+(x3y4-x4y3)k，而圆孔的轴线向量为：n=[(y3z4-y4z3),-(x3z4-x4z3),(x3y4-x4y3)]。

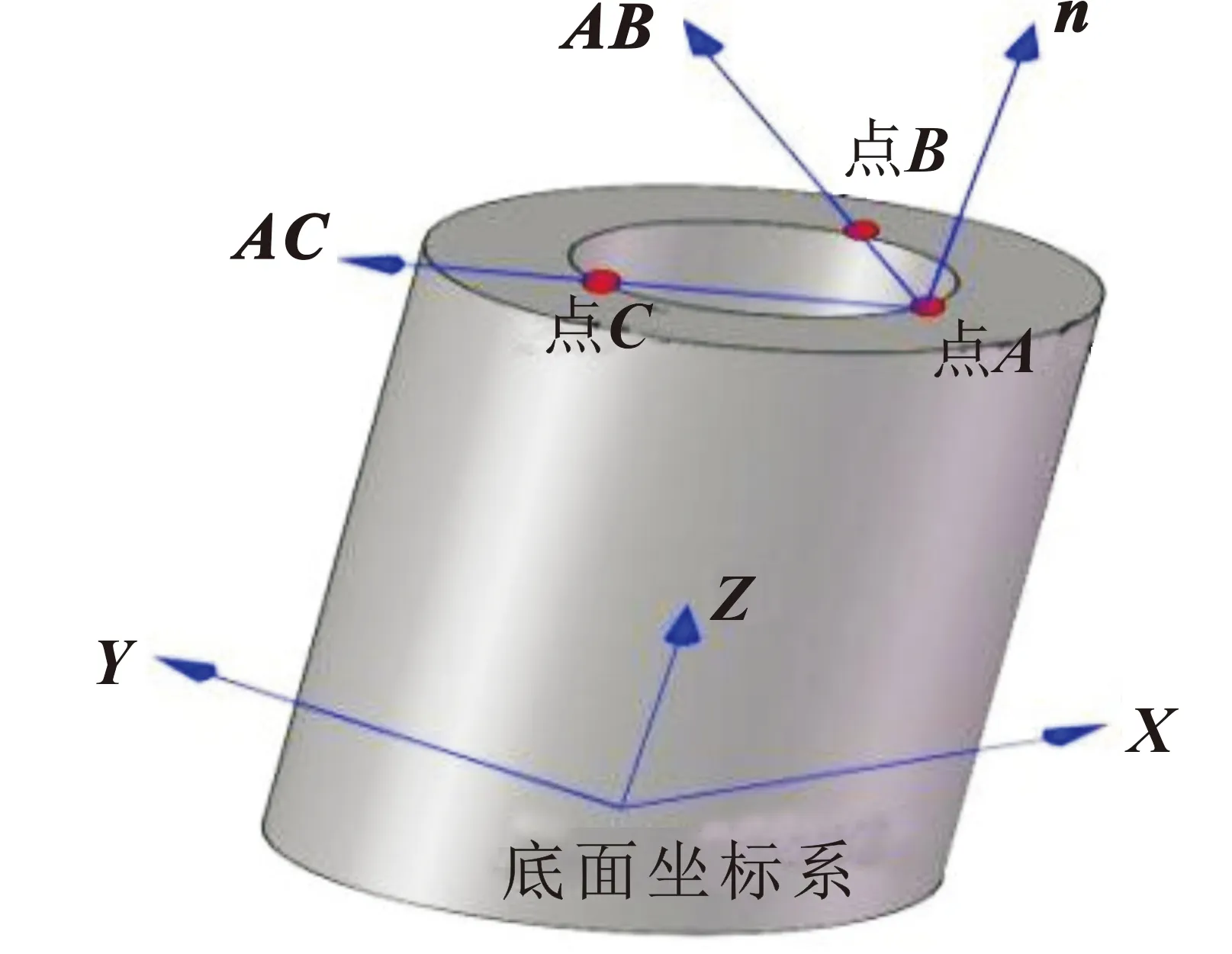
图7 计算孔端面法线示意Fig.7 Schematic of calculating the normal of hole end face

求得圆孔轴线后便可计算得出圆孔位姿，计算过程如下式：

(13)

其中：α、β、γ分别是圆孔轴线向量与世界坐标系xW、yW、zW的夹角。i=(1,0,0)、j=(0,1,0)、k=(0,0,1)分别为空间各坐标轴的单位向量。

2 实验与分析

为了验证文中所提出的基于工业机器人的图像引导圆孔定位检测方法的有效性与高精度。文中将搭建单目立体视觉系统，并对平面直孔工件进行检测验证。系统硬件包括：(1)AUBO-I5六轴机器人，最大工作半径为886.5 mm，定位精度可达到0.02 mm。(2)大恒MER-502-79U3M工业相机，分辨率为2 448像素×2 048像素，帧率为79帧/s。(3)相机镜头为50 mm定焦镜头。其中手眼相机的安装方式为眼在手上。系统软件程序平台为Visual Studio 2017 C++与MATLAB2018a，其中在MATLAB上将实现双目标定、图像立体校正等前期工作。而文中所提出的主要算法将由OpenCV在Visual Studio 2017上实现。系统构成如图8所示。

图8 系统构成Fig.8 System configuration

2.1 孔轮廓检测提取实验

为了验证文中提出的基于弧段的椭圆检测算法在实际工作场景中应用的性能与准确性，文中将对所要检测的孔板工件进行实验。为了清晰地展示提取孔轮廓的过程与效果，图9只展示孔板工件其中一个孔。图9(b)为经过Canny算子进行边缘提取后的轮廓弧段图像，其中包含了大量的短弧、直弧等伪弧。通过筛选候选弧段，得到了图9(c)，但是仍含有伪弧。图9(d)为通过弓弦比的方法去伪后的轮廓弧段，图9(e)为传统的霍夫变换得到的椭圆拟合效果，图9(f)为运用椭圆平行弦中线定理进行椭圆拟合的效果。可以看出：由于椭圆轮廓的残缺，传统的霍夫变换算法拟合的椭圆远离了真实的椭圆边缘；而文中算法有效克服了由于边缘残缺而导致椭圆检测算法失效的问题。并且还可以看到运用文中所提出的椭圆检测算法得到的椭圆曲线十分接近圆孔的轮廓，可见文中算法行之有效。

2.2 极线约束立体匹配实验

图10所示为AUBO-I5六轴机器人带着手眼相机在2个水平位置采集的图像，经过SURF特征点检测，再经过RANSAC算法提纯的效果图。

图10 立体匹配效果Fig.10 Stereo matching effect

经过SURF特征点检测与RANSAC算法误配点提纯后得到212对精确匹配点，但是大多数匹配点都分布在工件边缘，而位于孔轮廓上的匹配点则寥寥无几，匹配点示意如图11所示。这将会导致关键视差信息缺失，影响后续三维重建工作。但是却可以通过这些匹配点计算出两幅图像的基本矩阵，用于下面的基于极线约束的立体匹配。

图11 SURF+RANSAC特征点检测效果

通过计算基本矩阵与两幅图像中像素点的关系可以得到基本矩阵F为

通过上述获得的圆孔轮廓边缘点信息与双目图像的基本矩阵，进行基于极线约束的立体匹配。文中将在孔板工件中选取一排3个孔轮廓进行实验，实验效果如图12所示。

图12 基于极线约束的立体匹配效果

从图12中可以看出：相比于传统的SURF+RANSAC特征点检测，对于金属弱纹理孔工件，采用文中算法可以精确地得到孔轮廓上的若干匹配点，解决了由于弱纹理导致的匹配点稀疏、关键视差信息丢失的问题。

2.3 孔位姿计算

通过第2.2节中实验得到的两幅图中对应的孔轮廓点对，根据第1.4节中相关原理以及孔轴线的求解方法，文中对孔心间距30 mm且水平放置的孔板工件进行实验，并对其中的以极线约束立体匹配后的3个孔轮廓进行三维重建，实验效果如图13所示。

图13 圆孔轮廓三维重建效果

从表1—表2中可以看出：通过文中方法检测得到圆孔工件参数，误差在1 mm以内；工件位姿参数误差在0.3°以内。

表1 重建孔位姿参数Tab.1 Reconstructed hole position parameters

表2 孔轴线向量与世界坐标系的夹角

为了验证文中方法的可靠性，对多组不同位姿的工件进行检测。通过机器人末端执行器得到的理论位姿与文中方法比较得出误差曲线如图14所示。

由图14可知：x、y、z坐标与孔心距的平均误差分别为0.67、0.65、0.68、0.6 mm，最大误差为1 mm；与世界坐标系x、y、z夹角的平均误差为0.22°、0.2°、0.21°，最大误差为0.3°。综上所述，文中所用的位姿检测方法具有较高的精确度与可信度，实现了对圆孔的高精度定位。

图14 位姿参数误差

3 结论

文中研究了一种基于工业机器人的图像引导圆孔定位方法，实现了对圆孔工件参数与圆孔工件位姿的高精度检测。提出一种基于弧段的椭圆检测算法，之后通过基于极线约束的特征点匹配得到了准确的双目图像匹配点，进而通过双目平行立体模型进行三维点计算与三维重建。实验分别验证了孔轮廓提取的鲁棒性，孔位参数与孔位姿检测的精度，并利用孔心距、与世界坐标系各轴夹角等参数进行精度评价。文中方法提升了对孔轮廓提取的鲁棒性，提升了通过图像引导进行参数与位姿检测的精度。通过实验表明，圆孔工件参数误差可达到1 mm以内，位姿误差可达到0.3°以内。满足目前工业领域对无损检测所需求的高效率、高精度等要求。