通信拓扑切换下的预定时间分组协同制导方法

马文卉，符文星，方洋旺，刘双喜，梁晓庚,3

(1.西北工业大学自动化学院，西安 710072；2.西北工业大学无人系统技术研究院，西安 710072；3.中国空空导弹研究院，洛阳 471009)

0 引 言

近年来，网络通信技术的发展改变了传统飞行器各自为战的模式，文献[1-3]对协同制导问题的研究开启了诸多学者对协同制导领域的探索。网络化的协同制导技术可通过信息共享实现协调配合、完成协同任务，因而广受关注。现今，防御手段快速升级迭代，多重对抗措施对飞行编队协同造成极大挑战，为执行多元化协同任务，编队扩编势在必行。然而，编队扩编势必会为通信能力带来挑战。受网络规模、通信距离、带宽、频点数量和外界干扰等多重因素制约，组网通信链路可靠性随着编队规模的增加而下降，固定通信网络拓扑结构极易断开。虽然架构灵活的分组协同能够充分发挥规模优势、在保证编队扩编的同时兼容饱和攻击或波次攻击等多重任务，但频繁的通信断信极大地威胁了系统稳定性，因此放宽分组通信约束、保证拓扑切换下的协同制导系统稳定性至关重要。随着一致性理论的发展，通信拓扑切换条件下的分组编队协同问题得到了广泛的研究[4-8]。文献[4]针对拓扑切换下的分布式分组时变编队跟踪控制问题开展研究，提出了一种集群系统模型框架：组领队承担组间通信职能，组内、组间采用无向通信。该方案能够保证拓扑切换下系统稳定，且分组结构易于工程拓展。文献[5]提出了适用于多目标的两阶段分组协同制导方案，有向分组通信相比于无向分组通信有利于减轻通信负担。但考虑到入度平衡假设的限制，进一步开展耦合分组方案研究更适用于多目标任务。

分组协同能兼顾多重任务需求，但编队扩编不仅会加重网络通信的负担，还会影响飞行编队协同效果，不充分的收敛会导致协同时间差、降低协同效能甚至导致任务失败。因此，快速、充分的收敛对于飞行编队来说至关重要。文献[9]基于有限时间一致性研究了无向分布式通信下的饱和攻击问题。文献[10]将协同制导问题转化为视线系下的剩余飞行时间协调问题，利用有限时间理论，提出拓扑切换下协同拦截方案。相比于渐近收敛[4-8]，有限时间协同制导方案[9-16]收敛速度加快，但收敛时间上界受初始条件限制，不适用于复杂的飞行编队协同任务。为此，诸多学者将目光转向固定时间理论的相关研究[17-21]。虽然固定时间方法能避免对初始条件的依赖，但难以兼顾收敛速度和收敛效果，通过参数整定保证收敛时间上界小于到达时间的固定时间方案不便于工程应用。另一方面，快速完成协同、转入独立制导阶段能从根本上避免通信干扰，实时判断系统收敛会浪费有限计算资源，因此，为针对性地协调通信资源，进一步探索预定时间协同制导方法具有工程价值。

综上所述，复杂环境下分组协同制导极大的受制于通信状况，飞行编队无法按理想的固定网络拓扑结构通信，实现拓扑切换下的快速收敛以保证协同打击是当前协同制导亟待解决的重要问题。针对上述问题，本文提出一种适用于通信拓扑切换场景下的预定时间分组协同制导方法。相比于已有方法，在拓扑切换的情况下，该方法的收敛时间可根据任务需求明确选定，理论上独立于飞行初始条件和制导参数。同时，利用牵制分组控制实现多目标分组打击，结合文献[22]的相关思路，基于M矩阵假设，构建便于规模拓展的有向耦合分组网络架构，利用小组领队飞行器通信保证“组内-组间”协同。

1 预备知识

1.1 图论

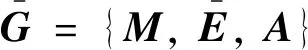
(1)

在此基础上给出M矩阵定义及引理如下。

定义1[1].对于非奇异矩阵W={wij}∈RN×N，若wij≤0,∀i≠j且其逆矩阵W-1的所有元素都非负，则矩阵称为M矩阵。

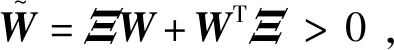
1.2 预定时间稳定理论

引入预定时间尺度函数如下

(2)

式中：h>1;t0为初始时刻；T>0为有限的系统收敛时间。对a(t)求导则有

(3)

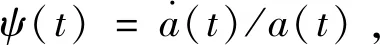
引理2[24].考虑如下动力系统

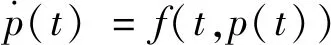
(4)

式中：p(t)∈Rn为状态变量；f(·,·)为有界向量场。系统存在某一Lyapunov函数V(t,p(t))连续可微，简记为V(t)且V(t,0)=0。当b≥0且k∈R+时，若满足

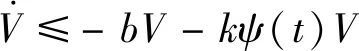
(5)

则系统全局预定时间稳定，即对于t∈[t0,t0+T)有

V(t)≤a-k(t)e-k(t-t0)V(t0)

(6)

且对于t∈[t0+T,∞),V(t)≡0。

2 问题描述

2.1 带有拓扑切换的分组通信网络

本文采用图1所示牵制分组策略进行协同，通过组领队飞行器之间的信息交流，分组协同根据实际需求可利用组间协同完成的任务类型包括但不限于同时打击多目标、时差到达某一特定目标或多目标。包含s个目标的目标集为T*={T1,T2,…,Ts}。飞行编队被划分为σ(σ≥max(s,2))个小组，记为MG={MG1,MG2,…,MGσ}。当mi属于第j(j=1,2,…,σ)个小组时，记Gi=j。选取部分小组领队无人机进行牵制，相应牵制矩阵记为D=diag(d1,d2,…,dN)。

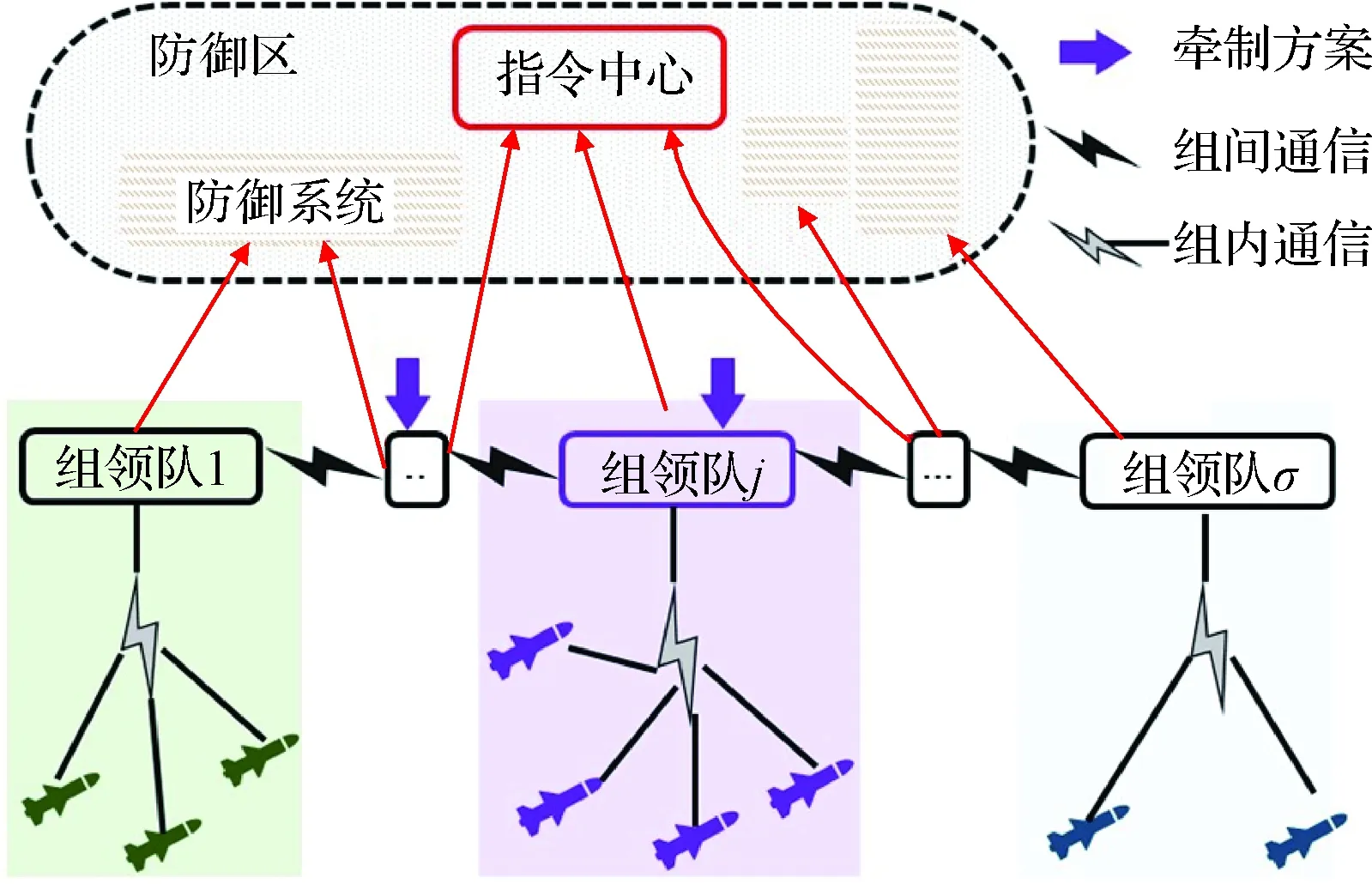
图1 牵制分组协同架构示意图Fig.1 Diagram of the pinning group cooperative structure

假设 1.在通信受限需要切换通信拓扑的情况下，分组及小组相应任务不随通信拓扑而改变，任意飞行器所属组不变，即系统状态量连续。

假设 2.在通信拓扑切换过程中，分组通信网络可通过牵制策略Dμ(t)以保证Υμ(t)=Lμ(t)+Dμ(t)始终为M矩阵。

2.2 协同制导建模

为建立协同制导模型，忽略飞行器和目标的姿态、视其为三维空间中质点，做出基本假设如下：

假设 3.末制导阶段飞行时间短，飞行器处于无动力飞行状态，即飞行器速度大小相同且保持不变，加速度向量方向与速度方向垂直用于调整速度方向。

三维协同制导几何关系如图2所示。其中，mi-XIYIZI为参考惯性坐标系；mi-XmiYmiZmi为飞行器体坐标系；mi-XLiYLiZLi为视线参考坐标系。飞行器mi的视线角和速度前置角分别使用(θLi,φLi)和(θmi,φmi)表示；LOS表示视线，Ri则表示飞行器mi与目标之间的相对距离；Vm和σi分别表示飞行器mi的速度和总前置角。

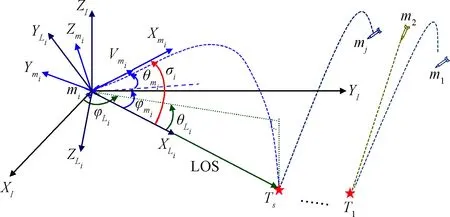
图2 三维制导几何示意图Fig.2 Three-dimensional guidance geometry

根据文献[26]和[27]，相对运动方程描述如下

(7)

式中：ayi和azi是mi在俯仰和偏航方向上的加速度；λyi和λzi表示惯性参考系中的视线角分量。

进而可将总前置角表示如下

σi=arccos(cosθmicosφmi),σi∈[0,π)

(8)

令Fi(t)=Ri/Vm和Hi(t)=-cosσi，构建飞行器协同制导系统状态方程如下

(9)

本文拟通过设计制导指令使得飞行器编队预定时间分组收敛并完成多目标协同打击，协同制导目标可具体表示为预定时间一致性目标，即

定义 2.任意mi,mj∈MGi(MGi⊂MGσ),分组预定时间收敛的协同打击在满足如下条件时成立：

(10)

且∀t≥t0+T,满足|Fi(t)-Fj(t)|=0,|Hi(t)-Hj(t)|=0。

3 拓扑切换下的预定时间分组协同制导律设计

设计预定时间协同制导指令如下

(11)

式中：Ui为第mi个飞行器的协同控制指令，其中带有拓扑切换牵制分组误差ε1i和ε2i为

(12)

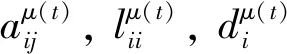
引理3[25].对于任意给定向量X,Y∈Rn×1，存在任意正定对称矩阵W∈Rn×n使得以下不等式成立

2XTY≤XTWX+YTW-1Y

(13)

引理4[4].对于任意正定实对称矩阵Q1,Q2∈Rn×n和任意向量Y∈Rn×1，有如下关系式成立

(14)

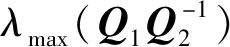
定理 1.通信网络拓扑切换时状态量连续，即满足假设 1时，采用预定时间协同制导指令(11)，通过牵制保证m次拓扑切换下Υμ(tρ)=Lμ(tρ)+Dμ(tρ),ρ∈{0,1,…,m-1}始终为M矩阵，且当t∈[t0,t0+T)时，存在制导律参数h>1,β1>0,β2>0满足条件(15)-(17)使状态量在拓扑切换下预定时间收敛。

qphλmin(Γμ(t))min(ξμ(t))>1

(15)

(16)

(17)

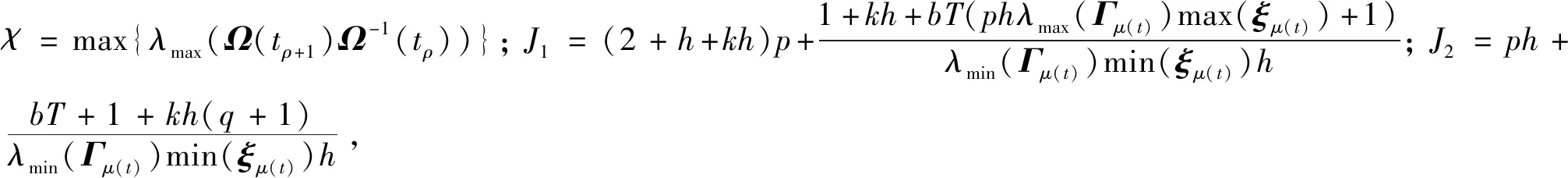
证明：首先，对系统进行状态变换。其次，证明[t0,t0+T)时拓扑切换系统在每个时间段[tρ,tρ+1),ρ∈{0,1,…,m-1}预定时间收敛，进一步证明拓扑切换点tρ预定时间收敛。随后，证明系统误差预定时间收敛、控制量有界，在t∈[t0+T,∞)时稳定性保持不变。

(1)系统状态变换

对于任意mi∈MGi记误差变量为

(18)

式中：状态量记为F=[F1,…,FN]T,H=[H1,…,HN]T，分组期望FG=[FG1,…,FGN]T,HG=[HG1,…,HGN]T。

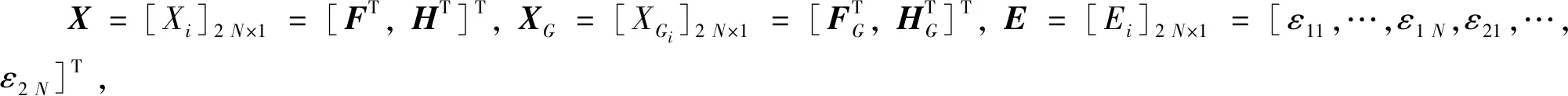
(19)

(20)

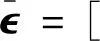
(21)

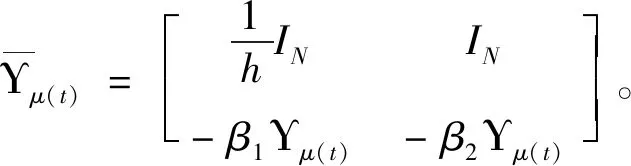
(2)t∈[tρ,tρ+1),ρ∈{0,1,…,m-1}时，协同制导系统预定时间收敛

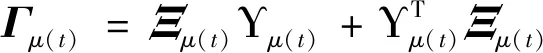
(22)

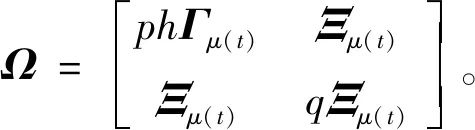
对Lyapunov函数(22)求导，得

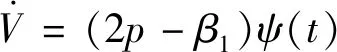
qβ2ψ(t)

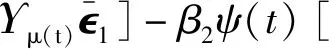
phψ(t)[

(23)

根据引理3，放缩则有

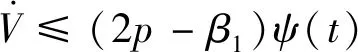
qβ2ψ(t)

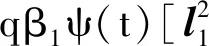
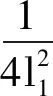
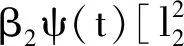
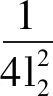
(24)

整理得

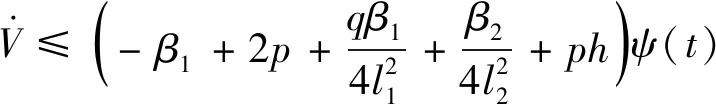
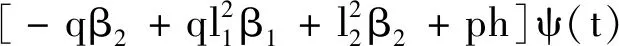
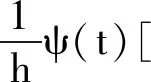
(25)

进一步放缩可得关系式如下

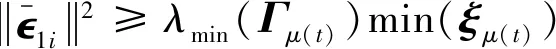
(26)

同理，有

(27)

同理，放缩Lyapunov函数(22)，得

V≤ph

(28)

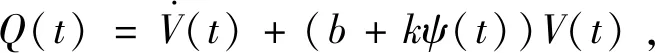
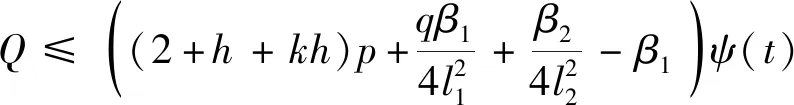
(29)

根据可行性条件，系数满足

(30)

进一步放缩有

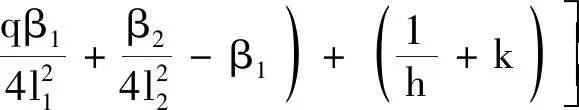
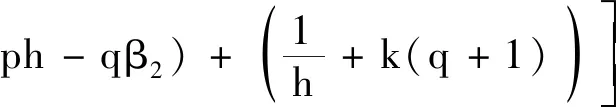
b[phλmax(Γμ(t))max(ξμ(t))+1]

b

(31)

根据可行性条件，可结合ψ(t)≥h/T放缩得

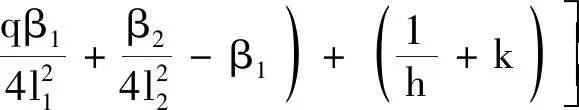
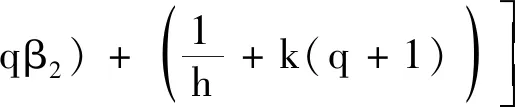
b[phλmax(Γμ(t))max(ξμ(t))+1]

b

(32)

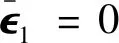
(33)

因此，满足预定时间收敛引理2条件可得：

V(t)≤a-k(t)e-b(t-tρ)V(tρ),t∈[tρ,tρ+1)

(34)

(3)tρ(ρ∈{0,1,…,m-1})切换时预定时间收敛

在切换时刻t=tρ

(35)

据假设 1，系统状态量连续，Ω(t)为正定实对称矩阵，由引理4有

(36)

即

(37)

将式(34)代入(37)，得

(38)

进一步递归得到

(39)

根据t-t0=t-tρ+(tρ-tρ-1)+…+(t1-t0)≥t-tρ+ργ0可得

b(t-tρ)]V(t0)

(40)

故系统预定时间收敛。

(4)误差预定时间收敛

根据Lyapunov函数可得不等式如下

(41)

同理，有

(42)

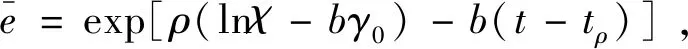
(43)

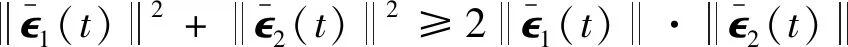
(44)

(45)

由于t→(t0+T)-时ψ(t)→∞,故

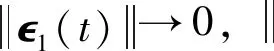
(46)

故误差预定时间t0+T收敛。

(5) [t0,t0+T)控制量有界性证明

令β=max(β1,β2)，则式(11)中U=[Ui]N×1得

‖U(t)‖=‖β1ψ2(t)Υμ(t)1(t)+β2ψ(t)

Υμ(t)

(47)

将式(44)代入(47)，则有

(48)

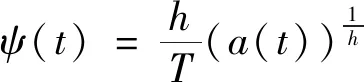
(49)

据定理1中的可行性条件kh(ρ+1)>2，则有

(50)

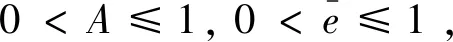
(51)

在[t0,t0+T)控制量U(t)有界。

(6) [t0+T,∞)状态保持且控制量为0

当t∈[t0+T,∞)时，ψ(t)=0，故有

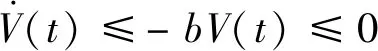
(52)

令t=t0+T

(53)

因此，

0≤V(t)≤V(t0+T)=0,t∈[t0+T,∞)

(54)

当t=t0+T时V(t)≡0，则1(t)=0,2(t)=0。则在[t0+T,∞)时有U(t)=0。故[t0+T,∞)时分组一致性保持，控制量有界且连续。

综上，通信拓扑切换下的多飞行器编队分组预定时间稳定性得证。

4 基于预定时间收敛的两阶段协同制导方案

通信环境复杂，尽早实现协同可以减少通信对制导的不利影响，降低潜在的任务负担，本文给出两阶段协同制导方案及其参数整定相关思路以增加工程可用性。

1) 采用预定时间分组协同制导律实现剩余飞行距离和总前置角误差的收敛以保证协同。

(55)

式中：

Δ1=max(sinφmi,δ1),Δ2=max(sinθmicosφmi,δ2),δ1和δ2为边界约束小量。

2) 当时间t=t0+T时，协同状态量协同一致，所有飞行器转至独立制导阶段，采用纯比例导引协同制导律如下：

(56)

式中：Kp为制导系数。

注 1.在接敌区域内，独立制导有利于避免通信强干扰导致的协同失败。在第一阶段协同变量收敛的基础上，第二阶段独立制导律可保持协同状态一致，从而实现既定的分组一致到达。将式(56)代入(8)，得

(1-Kp)Vmsinσi/Ri

(57)

因此

(58)

从而得到

(59)

代入(57)则有

(60)

因此第一阶段结束时协同状态量一致，第二阶段初始状态相同，当Kp≥2时，独立纯比例导引律引导飞行器到达目标。

在此基础上给出参数整定相关思路，实施过程中，需要实际给定的参数可分为如下几类：

(1)预定时间参数：t0和T，根据实际任务需求事先设定。

(3)制导律控制参数：h,β1,β2和Kp，其中h用于调节预定时间收敛速度；β1和β2调节误差收敛速度;Kp用于调节第二阶段纯比例导引指令。

注 2.为进一步简化制导律参数选择，则令β2=ηβ1(η>0)，根据式(16)可得

(61)

因此，可通过调节参数η确定β1取值范围，从而选择合适的制导律控制参数β1和β2。

5 仿真校验

本节针对不同的场景开展带有拓扑切换的预定时间协同制导方法的仿真校验。

5.1 同时打击不同目标

该仿真算例中，两个目标分别位于(0 km,1 km,0 km)和(0 km,-11 km,0 km)，由7个飞行器组成的编队被分为2个小组用于实现对多目标的协同打击。编队飞行器的飞行速度为500 m/s，过载约束±10，前置角约束为|θmi|<45°,|φmi|<45°。分组情况及初始条件给定如表1所示。

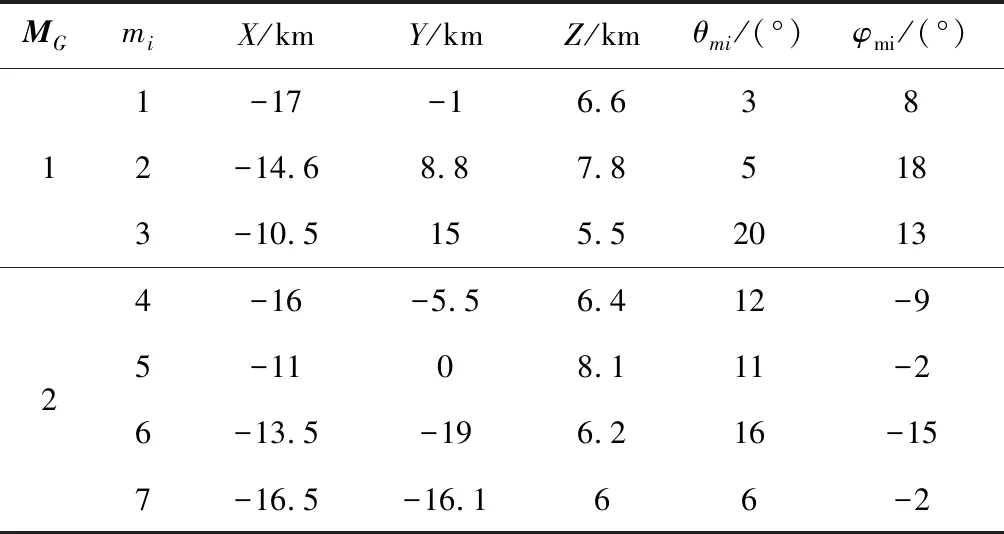
表1 仿真算例1仿真初始条件Table 1 Initial conditions of Case 1

分组同时到达不同目标则期望状态量一致,构建虚拟组期望FG1(0)=FG2(0)=F1(0)=36.9,HG1=HG2=-0.9。选择组MG1中的m1和组MG2中的m4进行牵制，即牵制策略可表示为

Dμ(t)=diag(1,0,0,1,0,0,0)

(62)

4种通信拓扑关系给定如下

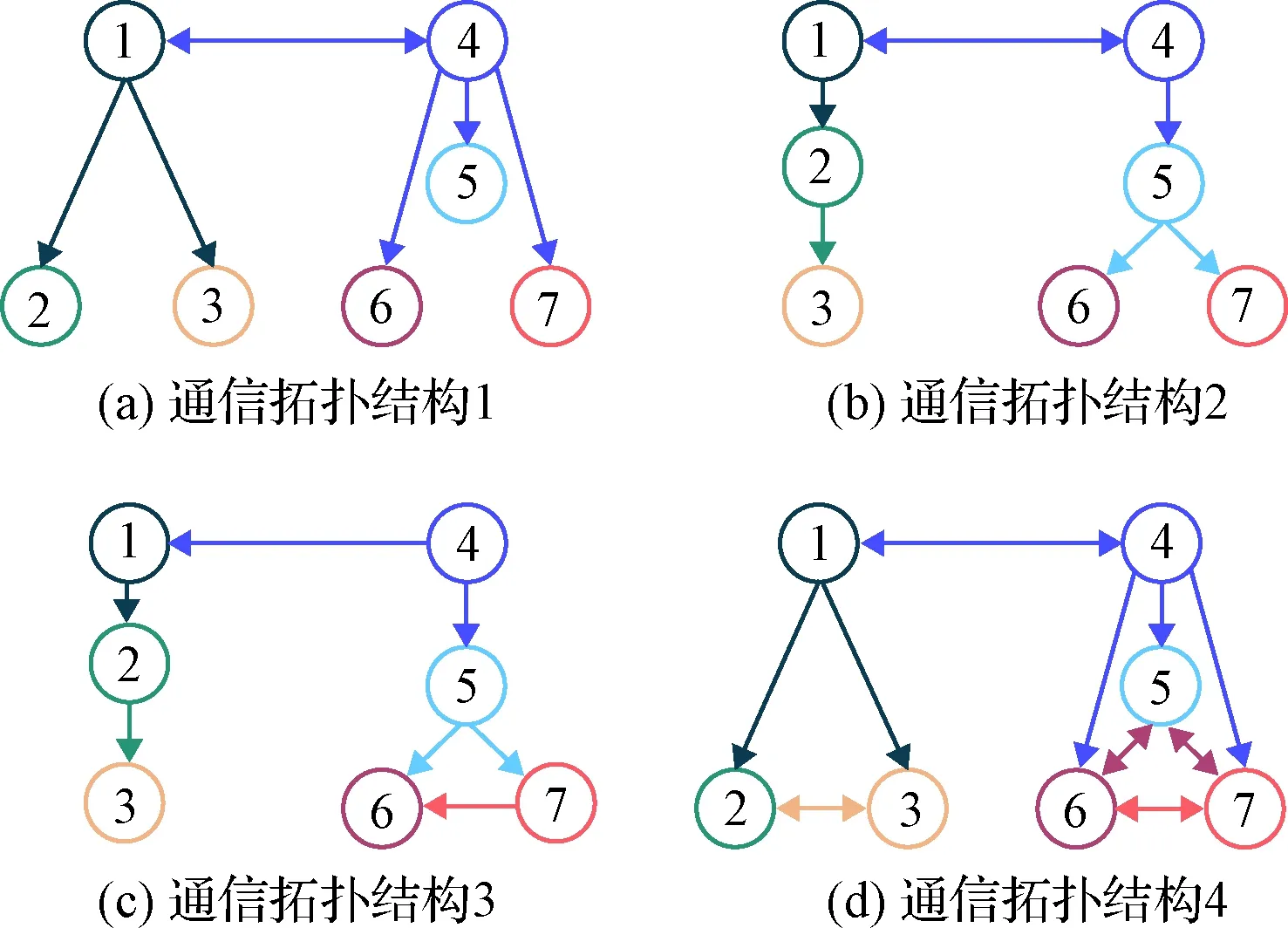
图3 仿真算例1通信拓扑结构Fig.3 Topologies of Case 1

通信拓扑切换序列如图4，Υμ(t)始终为M矩阵。

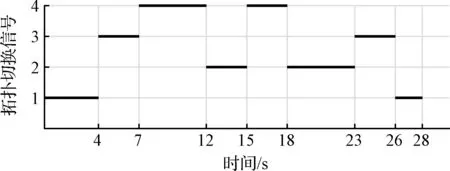
图4 仿真算例1通信拓扑切换信号Fig.4 The switching topology index of Case 1

设置参数如下T=28 s,h=4,β1=0.55,β2=1,Kp=6。仿真结果如图5所示。

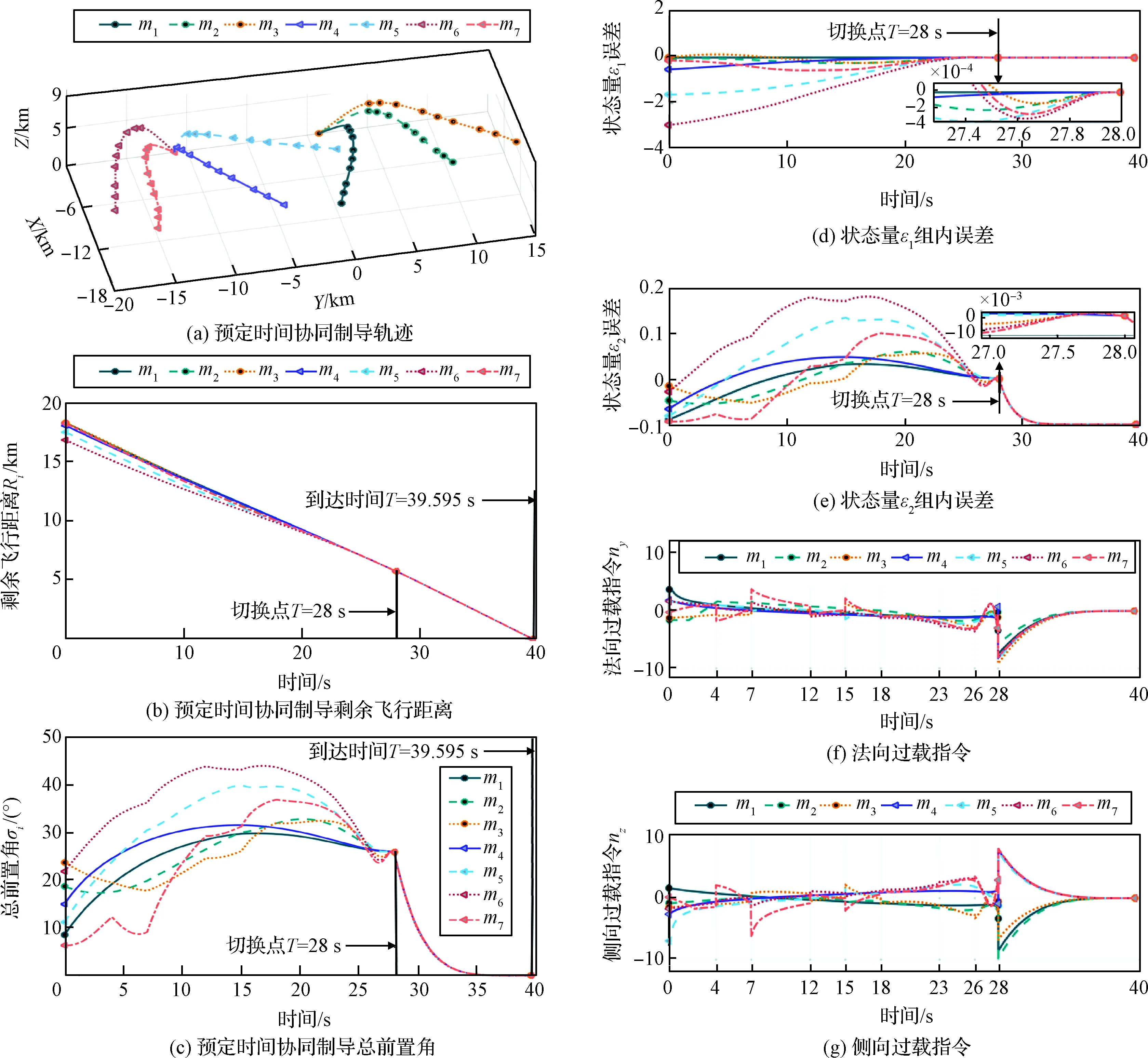
图5 预定时间协同制导仿真结果Fig.5 Simulation results of PTCGL

仿真结果表明，在通信拓扑结构切换的情况下，两组飞行器在本文提出的制导律作用下按照期望在T=28 s时实现分组协同状态量收敛，在39.595 s时两组同时击中不同目标，脱靶量小于2 m。

为进一步验证预定时间分组协同制导方法的有效性，基于协同制导律(11)，以文献[22]中的分组一致性协议为对照，给出基于分组一致性的传统分组协同控制指令如下

(63)

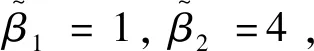
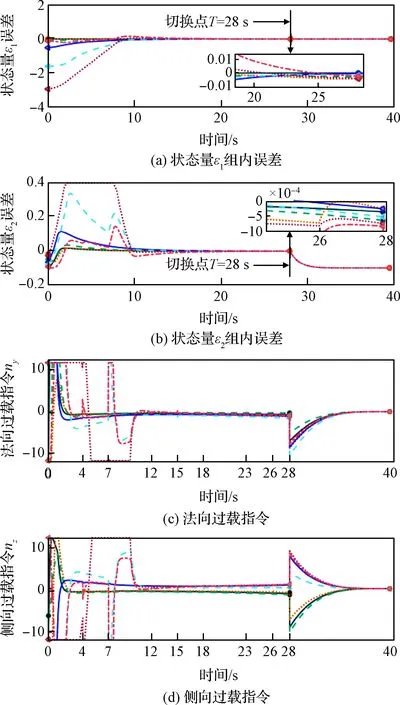
图6 传统协同制导仿真结果Fig.6 Simulation results of traditional cooperative guidance

仿真结果表明，传统协同制导方案，可于39.595 s按分组期望实现协同分组打击，脱靶量小于2 m。该方案在28 s处转阶段，状态变量分组误差分别小于0.01和0.001，飞行过程中，为保证收敛速度，飞行前期过载指令较大达到过载限幅±10且总前置角达到60°，即两方向前置角均达到限幅45°。

预定时间协同制导方案在拓扑切换条件下体现了更佳的收敛效果，即可根据任务需求实现预定时间收敛。传统渐近一致性方案虽然能通过调参满足切换条件，但较大的控制增益容易使执行机构达到物理限幅，难以兼顾收敛速度和收敛效果。本方案可保证系统快速且充分的收敛，易于施用。

5.2 波次打击

仿真算例中，两个目标分别位于(0 km,1 km,0 km)和(0 km,-11 km,0 km)，包含7个飞行器的编队被分为3个小组，其中，第一组和第二组同时到达不同目标，第二组和第三组构成对同一目标的波次攻击。飞行器飞行速度300 m/s。过载约束±5，前置角|θmi|<45°,|φmi|<45°，编队分组及初始条件给定如表2所示。

表2 仿真算例2仿真初始条件Table 2 Initial conditions of Case 2

四种通信拓扑关系及对应牵制策略给定如下

图7中,m1,m4和m6分别为小组领队飞行器，承担组间通信任务，小组领队无人机背景黄色即表示当前牵制策略选定该领队无人机施加牵制控制。通信拓扑切换序列如图8所示，Υμ(t)始终为M矩阵。

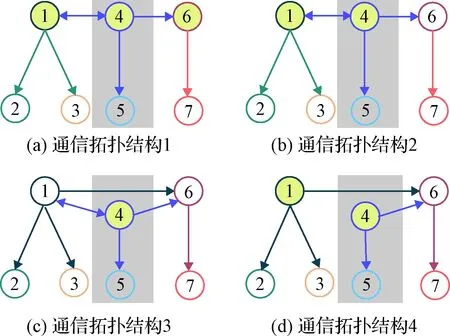
图7 仿真算例2通信拓扑结构Fig.7 Topologies of Case 2

图8 仿真算例2通信拓扑切换信号Fig.8 The switching topology index of Case 2

设置参数如下T=45 s,h=4,β1=0.6，β2=1,Kp=5两组分组同时到达不同目标，给定虚拟组期望FG1(0)=FG2(0)=60,HG1=HG2=-0.9，两组时差打击相同目标FG3(0)=63,HG3=-0.85。仿真结果如图9所示，结果表明在通信拓扑切换的情况下，三组飞行器在本文提出的制导律作用下按照期望在T=45 s时实现分组协同状态量收敛，在64.715 s时两组同时击中不同目标，在70.152 s时第三组协同到达目标，与前组对同一目标构成时差约5.5 s的波次攻击，脱靶量均小于2 m。

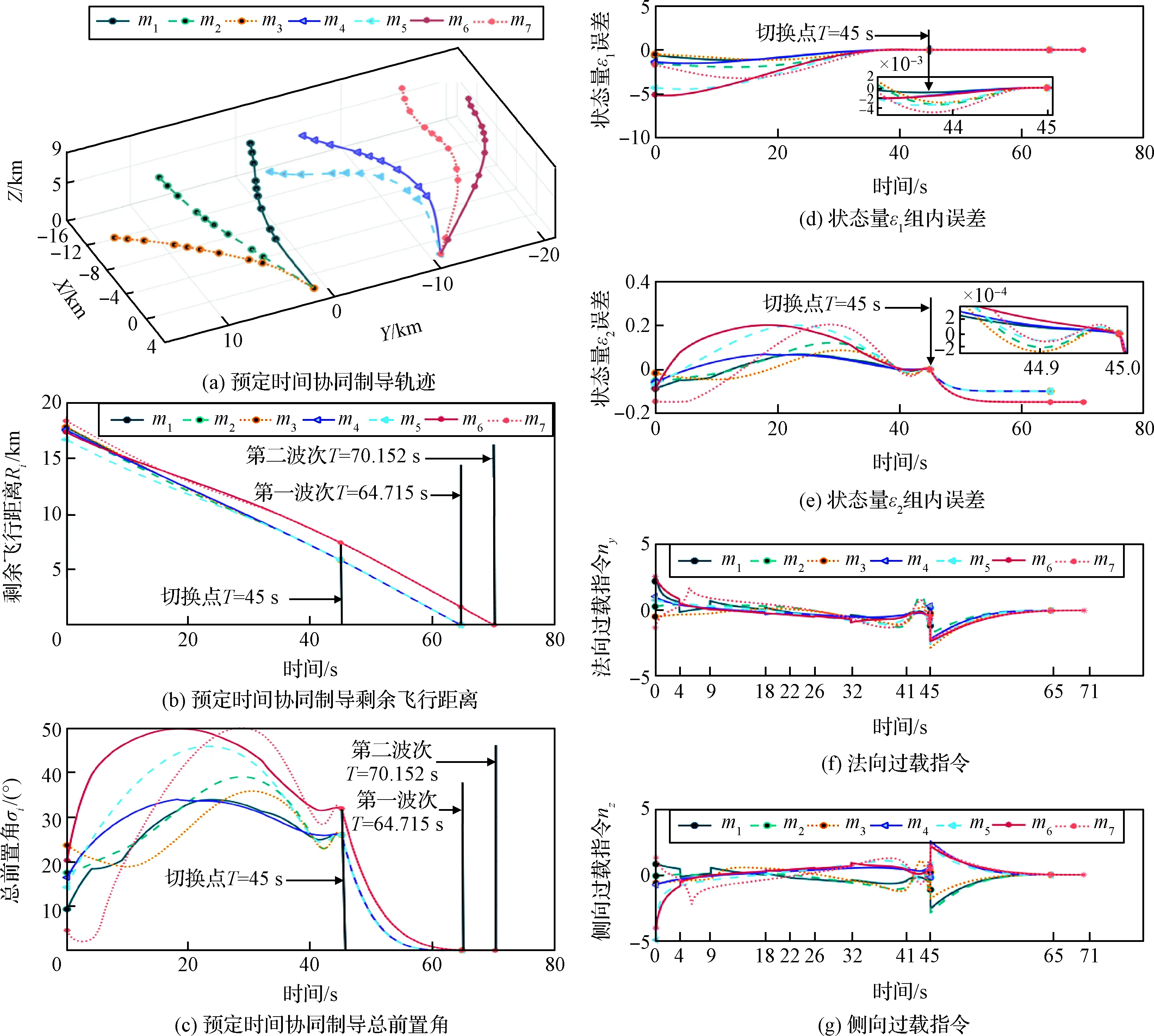
图9 仿真算例2仿真结果Fig.9 Simulation results of Case 2

6 结 论

为实现通信拓扑切换下的协同制导，本文提出一种预定时间分组协同制导律。该制导律一方面通过牵制控制放宽对分组通信网络的相关约束；另一方面，利用预定时间尺度函数实现分组协调变量的预定时间收敛。理论上，在拓扑切换的情况下，本文所设计的协同制导律可独立于初始条件和控制参数、根据任务指定收敛时间。在此基础上，为增加工程可用性，本文进一步给出两阶段预定时间协同制导方案并明确参数整定的相关思路。仿真校验结果表明本文提出的协同制导方案切换时间明确，第一阶段制导律可保证有向通信网络拓扑切换下的预定时间分组收敛，为第二阶段提供良好的初始状态；第二阶段制导律可通过保持协同状态一致完成分组协同任务。未来拟进一步针对通信延迟、断讯等复杂网络问题影响下的协同制导方案开展研究。