太极二号卫星精密热控关键技术及试验验证
2023-02-28冯建朝张晓峰侍行剑蔡志鸣
冯建朝,张晓峰,2,梁 鸿,侍行剑,何 涛,蔡志鸣
(1.中国科学院微小卫星创新研究院,上海 201304;2.哈尔滨工业大学能源科学与工程学院,哈尔滨 150001)
0 引 言
宇宙中存在大量的引力波源,包括起源于宇宙早期暴涨、反弹的原初引力波,宇宙早期相变产生的相变引力波,到黑洞、中子星系统并合产生的引力波等,覆盖了从10-18Hz到104Hz的宽阔频段。天体来源的引力波按照其质量等特征量的改变具有非常宽广的频段,从小于微赫兹至千赫兹跨越约10个量级。中低频(0.1 mHz~1 Hz)波源的特征质量大,引力波强度强,因此其探测范围可覆盖几乎全宇宙空间(红移z≈12)。探测这个频段的引力波需要摆脱地面噪声和地面实验尺度的限制,在太空实现百万公里级精密激光干涉测量。
中科院空间引力波探测团队提出的“太极计划”要求星间激光干涉测距噪声小于等于8 pm·Hz-1/2以及无拖曳控制残余加速度扰动小于等于3 fm·s-2·Hz-1/2,并制定了太极计划三步走路线图,从“太极一号”、“太极二号”到“太极三号”三星,通过对太极关键技术进行全系统、全功能、高指标的在轨验证,逐步提高其成熟度、可靠性及在轨适应性,最终实现空间引力波探测任务[1]。
上述两个顶层指标的实现要求航天器精密温控技术在敏感区域实现温度波动小于等于10 μK·Hz-1/2。2019年在近地轨道的太极一号(TJ01) 上已实现温度波动小于等于1 mK@1000 s[2-3],并将在未来深空轨道的太极二号上实现温度波动小于等于100 μK·Hz-1/2@10 mHz~0.1 Hz。影响太极二号卫星敏感区域温度稳定度的因素主要包括两个:太阳常数变化和卫星内部电子学单机热耗的变化。其中,由太阳常数引起的热源扰动约为2 W/(m2·Hz1/2);卫星平台提供的热边界相对复杂,通过后期整星级热设计,可以满足温度场波动小于等于±2 K。
上述温度指标对精密测控温技术提出了很高要求,由于非接触式测温存在理想黑体假设,实际测量时带来的理论偏差导致测温分辨率无法达到μK级[4],因此学界在精密测控温技术中普遍采用接触式测量方案。上海交通大学新型光通信系统国家重点实验室,使用分光仪通过测量温度导致的向列晶体(NLC)微小形变,实现了3 μK的测量分辨力[5]。石英晶体的固有频率随温度变化而变化,利用此特性可以进行温度测量,美国Quartzdyne公司生产的QT系列石英晶体温度传感器最高频达7.144 MHz,理论的测温分辨率可达100 μK[6]。基于调制电流电桥法,德国Max-Planck研究院使用热敏电阻作为传感器实现了地面短期±3.5 μK的温度测量分辨力[7]。美国加州大学伯克利分校使用热敏电阻在中心温度点35 ℃附近获得了长期10 μK的测量分辨力,NASA也在试验室条件下获得了50 μK的测量分辨力[8]。
实现高精度温控指标需要高效热防护系统,南京航空航天大学黄杰等[9]提出了热防护系统分区协调耦合推进方法,通过调节热防护系统的涂层发射率、材料导热系数、防热瓦厚度等,提高了热防护系统的隔热性能。哈尔滨工业大学孟松鹤等[10]对热力耦合约束下一体化热防护的结构尺寸优化与材料优选方法进行了详细介绍,并探讨了一体化热防护发展的特点和不足。汉森物理实验室Higuchi等[11]采用多级热防护方法,通过地面验证试验,在1 mHz频点处,实现了热控制系统对环境热扰动抑制1000倍的效果。
精密测控温技术在航天器上的应用也日渐增多,欧洲宇航局在2009年5月14日发射的“赫歇尔”卫星的远红外光学系统实现了工作温度的稳定度 30 mK/100 s,波动范围小于±0.5 K[12]。詹姆斯韦伯空间望远镜通过主动控温将NIRCam探测器温度控制在1 mK附近[13]。国内高分二号卫星相机主要光机部件在轨温度稳定度最高优于±5 mK[14]。欧空局LISA Pathfinder核心部件上的热控制系统可以实现10 μK·Hz-1/2@1 mHz的测量精度,20 μK·Hz-1/2@1 mHz的控温精度[15]。法国国家航天研究中心(CNES)“Microscope”卫星的核心载荷FEEU和SU的120轨内变化范围分别为20 μK和15 μK[16]。2019年,中国科学院微小卫星创新研究院,为满足太极一号卫星核心测量平台±0.1 K的精密控温需求,设计了多级辐射式控温方案,最终实现了±0.5 mK的控温精度[17-18]。
目前国内航天应用的精密测控温技术仍与引力波探测航天器的需求相差2~3个数量级。为了实现100 μK·Hz-1/2@10 mHz~0.1 Hz温度波动指标,太极二号航天器精密温控团队提出了多级热阻尼控温方法。围绕该种方法,如何建立多级阻尼系统状态空间的数学模型,明晰热扰动在复杂结构中的传递机理,并进行试验验证,是本文的主要研究内容。
1 基于传递函数的多级阻尼热控方法
太极二号采用核心舱和外围舱体分区控温与热弹稳定设计。太极二号核心舱构型布局如图1所示,分为三层结构:核心舱板及套筒、载荷壳体(隔热罩)及镜筒、光学组件及电极笼。
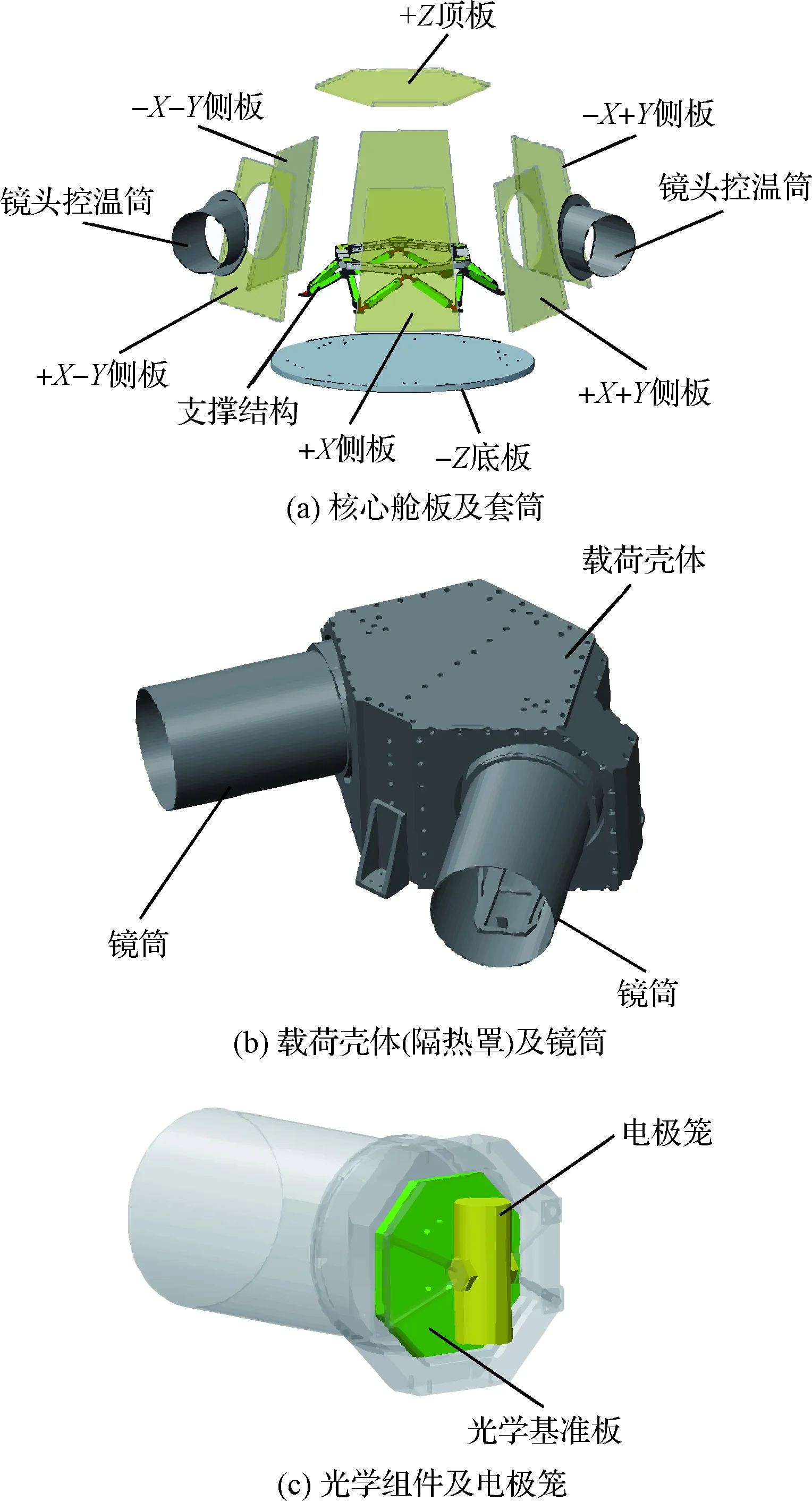
图1 太极二号核心舱构型布局Fig.1 Layout of the Taiji-2 core module
1.1 控温数学模型
太极二号核心舱热设计的主要思路为多级热阻尼控温,即将太极二号热模型等效为多级热阻尼模型,如图2所示。图2中T0,n为边界温度,R1,i,C1,i分别为热阻尼层1的热阻、热容,R2,j,C2,j分别为热阻尼层2的热阻、热容。

图2 多级热阻尼模型Fig.2 Multistage thermal damping model
采用R-C热网络法对上述模型进行分析,将核心舱所有组件离散化为具有特定热容的节点C。将各节点间的辐射、导热等换热关系用热阻R来表示,可得第i层阻尼的第j个节点的热模型如下式所示:
(1)
式中:Ti,j为第i层中第j个节点的温度;Ri,k&i,j为第i层中第k个节点与第i层中第j个节点间的热阻;Ci,j为第i层中第j个节点的热容;Qi,j为第i层中第j个节点的自身热源。
假设系统有n层阻尼,每一层划分为m个节点,则系统的状态变量为:
T1(t),T2(t),…,Tmn(t)
(2)
为了创建系统的状态空间,将系统的边界离散为q个算数节点,作为输入:
x1(t),x2(t),…,xq(t)
(3)
假设系统中关注的节点个数为L个,作为系统输出:
y1(t),y2(t),…,yL(t)
(4)
则可得系统的状态方程如下式:
(5)

T′(t)=AT(t)+Bx(t)
(6)
热阻尼系统的L个输出,也可以写成N个状态变量:
(7)
简写为:
y(t)=CT(t)
(8)
式中:C为输出矩阵,表达了输出向量与状态向量间的关系。
在复频域上求解热阻尼系统的状态方程,经过拉氏变换化简后可得:
T(s)=(sI-A)-1T-(0)+(sI-A)-1Bx(s)
(9)
解析后,可得系统函数矩阵为:
H(s)=C(sI-A)-1B+D
(10)
综上分析,H(s)即为热阻尼系统的传递函数矩阵,其求解的关键是矩阵(sI-A)-1,即阻尼系统网格节点的热容C和节点间的热阻R。
热容C取决于自身材料的比热和尺寸大小,其数值容易获取。热阻R均包括辐射热阻和导热热阻,其中,辐射热阻R不仅与材料表面辐射特性和角系数相关,还和表面的温度相关,且呈四次方关系,较为复杂。
为了简化计算,下面对辐射项进行线性化处理:

(11)
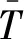
(12)
化简后,可得:
(13)
通过创建多级阻尼系统的状态空间,可对太极二号核心舱的温度场状态进行计算与分析,求解热扰动在模型中的传递特性,进而指导太极二号卫星的热设计。
1.2 系统特性分析
基于太极二号卫星核心舱热设计的需要,对热阻尼系统进行定性分析,将其简化为如图3所示R-C热网络。

图3 核心舱R-C热网络Fig.3 R-C thermal network of the Core module
核心舱简化模型的热网络方程如下:
(14)
计算可得,系统传递函数矩阵如下:
(15)
令上式中的s=ωj,并简化为如下形式:
(16)
幅频特性为:
(17)
相频特性为:
(18)
上式中:
a=(C1R1+C2R2+C2R1)ω
(19)
b=1-C1R1C2R2ω2
(20)
综上理论分析,可将太极二号核心舱多级热阻尼特性总结如下:
1)频率为ω的环境温度T0的波动幅值传递到单机时,温度波动幅值衰减为原来的|H(ωj)|,其具体数值由系统参数R,C和信号频率ω确定;
2)温度波动信号传递到单机时,不仅其幅值会有一定的衰减,波动相位也会产生延时,具体值为∠H(ωj),同样也由系统参数R,C和信号频率ω确定;
3)当多级阻尼系统参数确定后,其衰减比随着环境噪声频率ω的减小而增大,这表明多级阻尼系统对于低频段的热噪声的阻尼能力降低;
4)对于相同频率的环境热噪声,系统的衰减比随着阻尼层热容C和热阻R的增大而减小,这表明增大热阻尼层的R和C均可以增强热阻尼系统的阻尼能力。
2 太极二号核心舱热设计
2.1 关键技术介绍
依据上述状态热模型及其特性分析,可知影响卫星高精度控制的因素很多,其中各种热源的扰动是主要因素。太极二号卫星核心区域精密热控涉及到的热源扰动包括电极笼的热源扰动、光学基准板的热源扰动、边界的热源扰动等,这些都可认为是精密控温的热源噪声。如何有效抑制这些复杂的热源噪声,涉及卫星核心区域精密热控的关键技术。为了攻克此项关键技术,本文主要从热源噪声模型、噪声抑制方法和控温方案设计三方面展开,如图4所示。

图4 关键技术攻关路线Fig.4 Key technologies roadmap
太极二号卫星热噪声传递模型如图5所示,热噪声源很多且传递路径较为复杂。以太阳常数波动引起的热扰动为例,其传递路径依次为太阳电池阵安装板、支撑结构和隔热罩,最终传递到核心器件。为了有效抑制复杂环境热噪声,本文提出了增大热阻尼和构建稳定热边界的协同控温方法。

图5 噪声传递模型Fig.5 Noise transfer model
在方案设计过程中,为了增大热阻尼,本文提出了三级热阻尼控温方法。为了构建稳定可调热边界,本文一方面采用TJ01星载高精度控温仪,对一级控温对象进行主动控温,降低平台热源扰动的干扰;另一方面在连接部件和隔热罩上布置微调分档式加热器,进行微小热量调控,以实现核心器件温度基准点调控目的。
2.2 热设计方案
太极二号核心舱采用三级热阻尼控温方案,具体如下:
1)第一级控温对象为核心舱板和遮光筒,控温目标为±0.1 K,以主动控温为主;
2)第二级控温对象为载荷隔热罩和镜筒,控温目标为5 mK·Hz-1/2@1 mHZ~1 Hz,以被动控温为主;
3)第三级控温对象为光学组件和电极笼,控温目标为100 μK·Hz-1/2@1 mHZ~1 Hz,以被动控温为主。
被动热阻尼设计中,均以增大辐射热阻和导热热阻为目的,不仅在材料选择方面进行了筛选,而且对组件的构型也进行了精细化的设计。
主动控温方案中,共设计了两类主动加热器:初级闭环加热器(Primary heater)和微调加热器(Fine tune heater),如图6所示。闭环加热器用于边界控温,微调加热器用于温区的调整和系统的温度稳定度的提升。
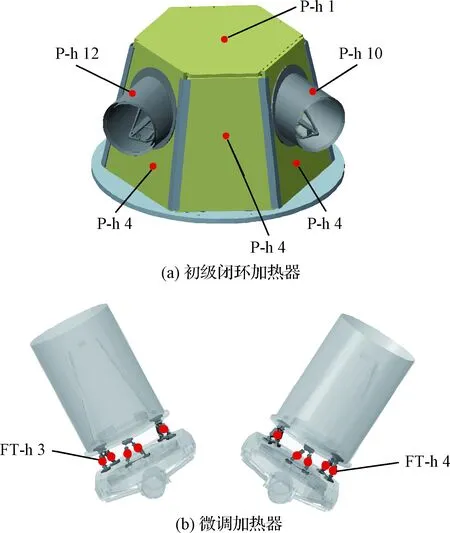
图6 主动加热器设计Fig.6 Active heater
在核心组件光学基准板(Optical bench)和电极笼(e-House assembly)上,布置了高灵敏度测温电阻,具体位置如图7所示。

图7 测温点分布Fig.7 Temperature measurement point distribution
3 载荷舱热控设计
3.1 热试验设备
太极二号核心舱真空热试验在卧式KM2真空罐内进行,如图8所示。试验设备主要包括:真空罐、直流电源、高精度控温仪、Fluke超级电桥、自研高分辨率测温样机等。

图8 真空罐内放置Fig.8 Placed in vacuum chamber
3.2 试验结果
为了匹配指标要求,需要将时域上的测试数据转换到频域进行分析。转换过程中,由于数据处理方法的不同,会使得分析结果略有差异。为了与国际引力波探测数据分析方法一致,本文将采用LISA团队开发的数据分析工具LTPDA[19],对测试结果的幅值谱密度进行线性拟合,并进行分析。
1)光学基准板
光学基准板的幅值谱密度曲线如图9所示,在10~100 mHz范围内,温度稳定度≤13.6 μK·Hz-1/2,优于太极二号卫星100 μK·Hz-1/2的指标要求;在1~100 mHz范围内,温度稳定度≤17.6 μK·Hz-1/2,与太极三号卫星的最终指标≤10 μK·Hz-1/2,仍有一定差距。

图9 光学基准板测试结果Fig.9 Optical bench test results
光学基准板的热环境,主要分为V型支架和隔热罩两部分,共有5个测温点,其中3个位于V型支架上,2个位于隔热罩上。5个测点处的温度波动如图10所示。在10000 s内V型支架的温度波动范围约为±200 μK,载荷隔热罩的温度波动范围约为±80 μK。

图10 光学基准板热环境Fig.10 Optical bench thermal environment
2)电极笼
在10~100 mHz范围内,质量块的温度稳定度≤11.5 μK·Hz-1/2,如图11所示,优于太极二号卫星100 μK·Hz-1/2的指标要求;在1~10 mHz范围内,温度稳定度≤73.1 μK·Hz-1/2,与太极三号卫星的最终指标≤10 μK·Hz-1/2,仍有一定差距。
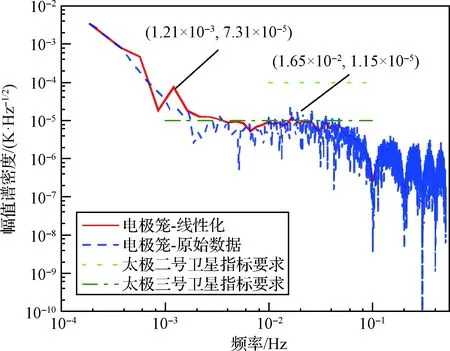
图11 电极笼测试结果Fig.11 Electric housing test results
电极笼热环境的测温点布局与光学基准板相同,5个测点的温度波动如图12所示,在10000 s内V型支架的温度波动范围约为±200 μK,载荷隔热罩的温度波动范围约为±80 μK。

图12 电极笼热环境Fig.12 Electric housing thermal environment
4 噪声分析
4.1 理论分析
对于太极二号引力波探测器而言,来自环境的任何热扰动都将是热噪声。本文将不同种类的热噪声统一归纳为温度信号。设f(x)是以2π为周期的温度函数,用三角多项式表示如下:
ancosnx+bnsinnx
(21)
式中:
(22)
(23)
温度函数按傅里叶系数展开后可得傅里叶级数如下:
(24)
这表明任意的周期性温度函数可以按照傅里叶级数展开。实际工程中的温度函数往往是非周期性的,需采用傅里叶变换进行处理,无限时长的非周期温度函数f(x)可在频域下表示为:

(25)
本次试验中,获取的温度信号为非连续的,假设采集点个数为M,则离散傅里叶变换式如下:
(26)
为了验证上述方法的可行性,以太极一号卫星实际在轨数据为例进行分析。某段时间内,太极一号卫星核心测量平台的温度变化曲线如图13(a)所示,时域温度波动幅值为±0.02 K。频谱如图13(b)所示,幅值较大的热噪声主要集中在低频段,频点f=0.005278 Hz时,噪声幅值最大为2.23 mK。
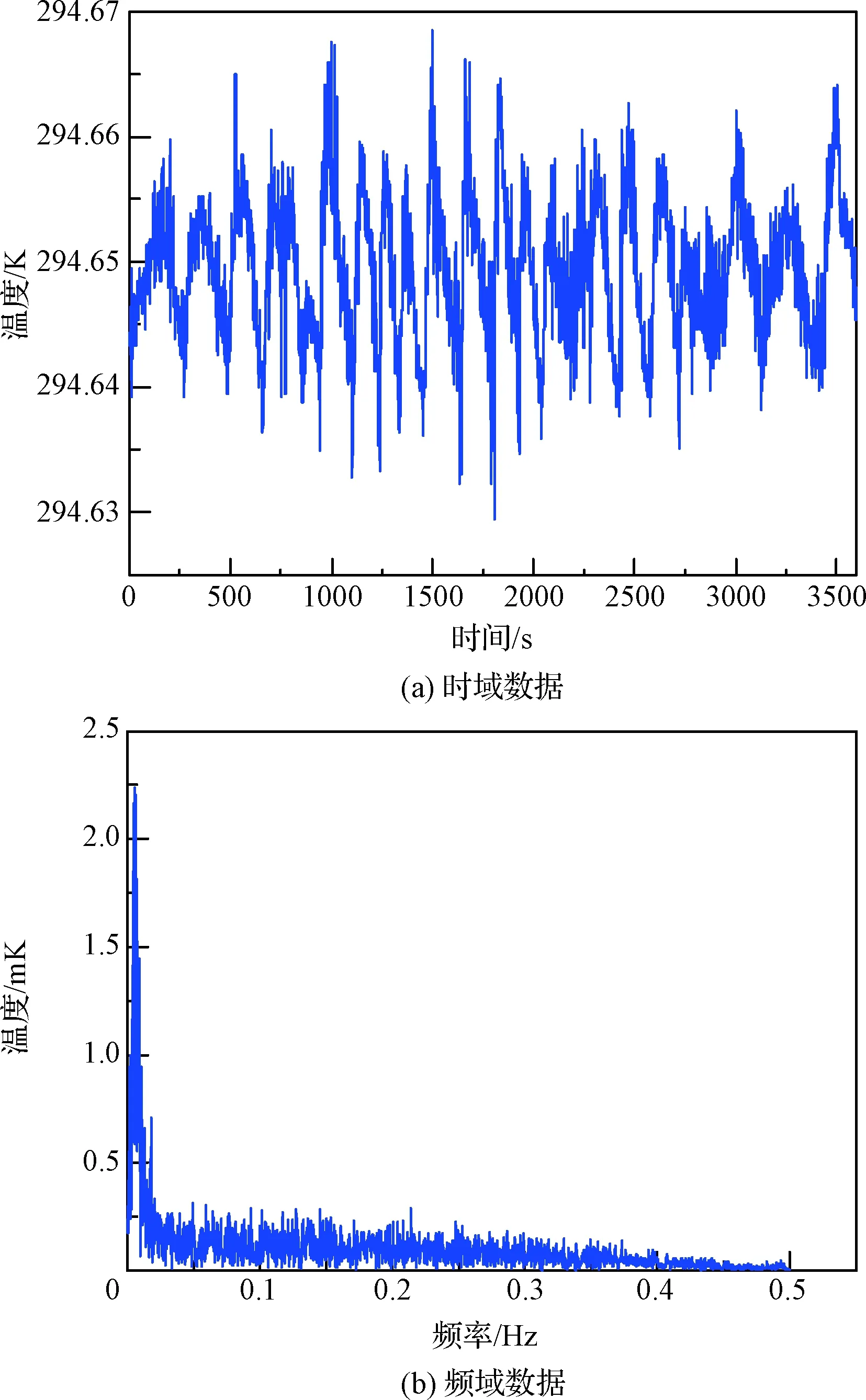
图13 太极一号在轨温度Fig.13 Taiji-1 on-orbit temperature
依据频率谱,进行时域上各频点下的噪声曲线拟合,如图14 (a)所示。将上述噪声曲线叠加后,与原始在轨曲线对比,如图14 (b)所示,频谱转换拟合曲线与实际在轨曲线吻合,表明温度曲线时频转换的方法正确可行。
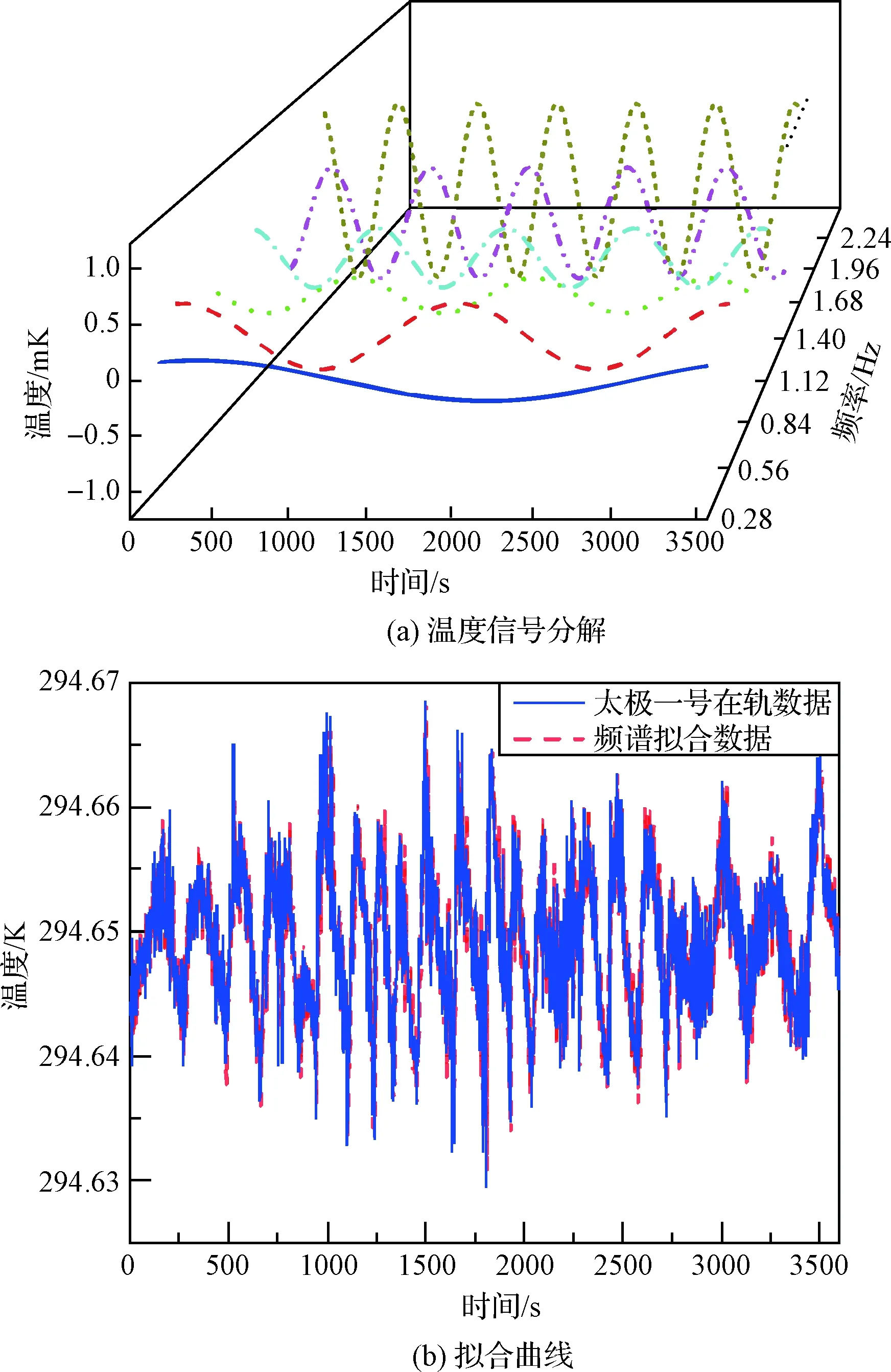
图14 太极一号温度频谱分析Fig.14 Taiji-1 temperature spectrum analysis
4.2 结果讨论
1)光学基准板
基于试验中获取的温度数据,对光学基准板测试数据进行频谱分析,如图15 (a)所示,噪声幅值最大值为4 μK,频点为0.96 mHz。而且可以发现,温度波动幅值大于1 μK的噪声均为低频噪声,集中在1~5 mHz范围内。按温度波动幅值大小选取最大的20个噪声频谱,如图15 (b)所示,这些噪声的频段主要集中在0.96~3 mHz范围内,幅值均≥1.5 μK,相位角的取值范围为3~3.3 rad。

图15 光学基准板温度频谱分析Fig.15 Optical bench temperature spectrum analysis
为了探究热噪声的传播途径,基于试验获取的温度数据对光学基准板热环境同样进行频谱分析,并选取0.96~2.88 mHz范围内,噪声幅值较大的20个频点进行分析,结果显示热环境中5个位置上的噪声频谱与光学基准板具有较高的重叠性,如图16所示。
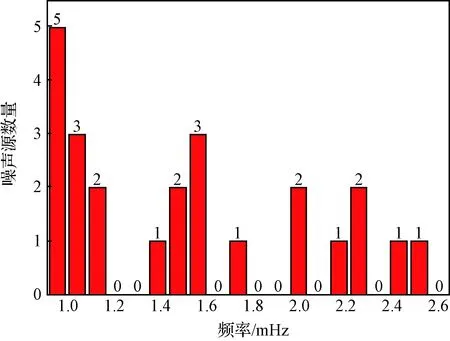
图16 光学基准板频谱重叠Fig.16 Optical bench spectral overlap
在不同频点处,光学基准板和周围环境的噪声频谱重叠个数并不相同,这主要来自以下两个原因:
(1)热环境的测温点数量有限,不能捕捉所有的噪声源;
(2)热环境中的噪声源与光学基准板自身的耦合。
总体呈现频率越低重叠个数越多的趋势,这进一步证明了随着频率的降低,热噪声传播穿透力逐渐增强。选取低频段内两个典型的频点作频谱曲线,图17(a)频率为0.96 mHz,图17(b)频率为1.05 mHz,可以看出,V型支架是光学基准板低频热噪声的主要来源。
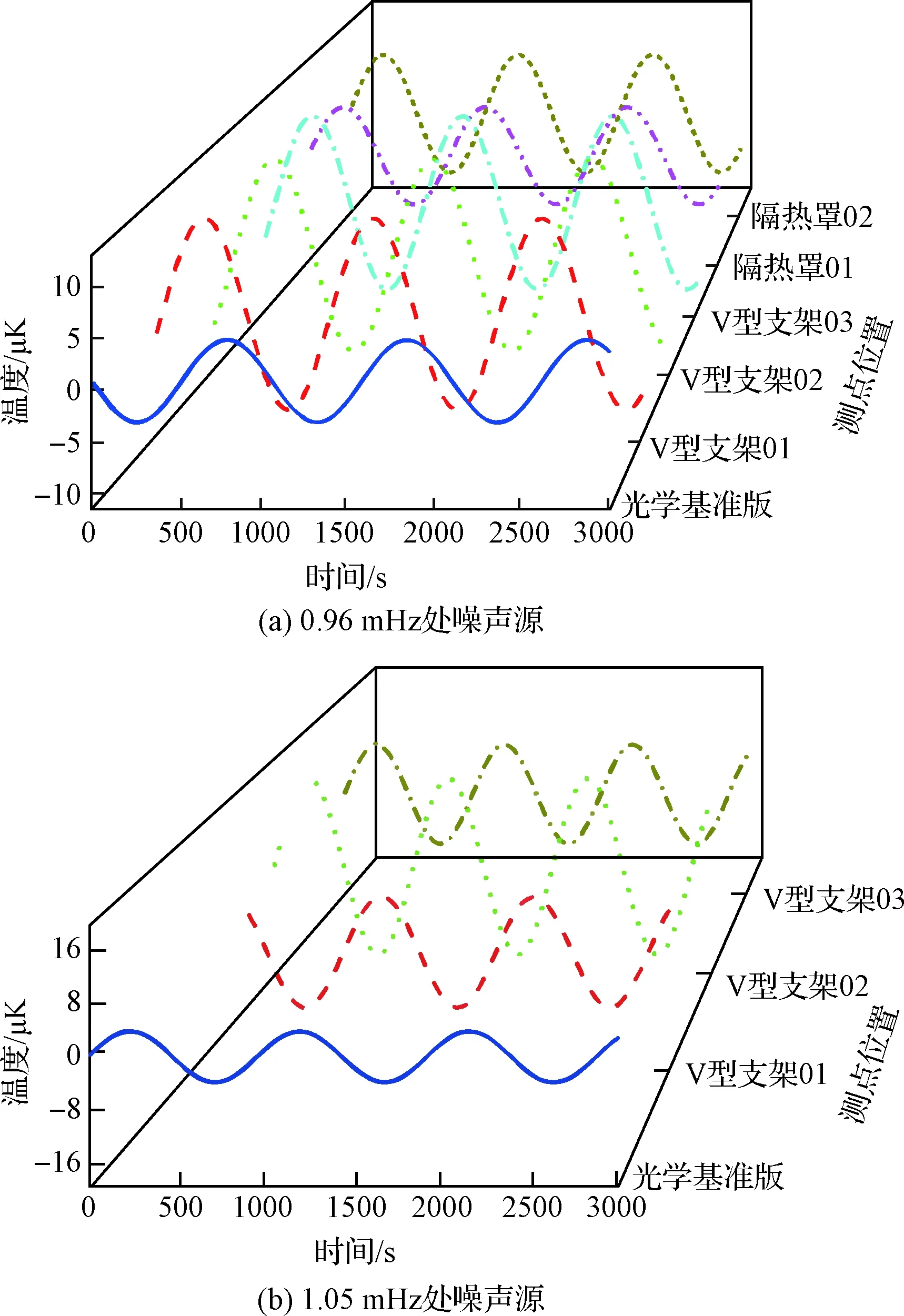
图17 光学基准板噪声源Fig.17 Optical bench noise sources
2)电极笼
采用同样的方法,基于试验中获取的电极笼温度数据,对电极笼温度进行频谱分析,如图18(a)所示,温度波动幅值最大值为11 μK,频点为0.94 mHz。进一步观察可知,电极笼温度波动幅值大于1 μK的热噪声均为低频噪声,主要集中在 1~5 mHz范围内。为了对噪声特性进行分析,按噪声幅值大小选取其中最大的20个噪声频谱,如图18(b)所示,这些噪声的频段集中在0.94~2.7 mHz范围内,幅值范围为3.8~11 μK,相位角的取值范围为3.1~3.2rad。

图18 电极笼温度频谱分析Fig.18 Electric housing temperature spectrum analysis
对电极笼热环境的温度曲线进行频谱分析,并选取0.94~2.63 mHz范围内噪声幅值较大的20个频点进行分析,同样发现热环境中5个位置的噪声频谱与光学基准板具有较高的重叠性,如图19所示。
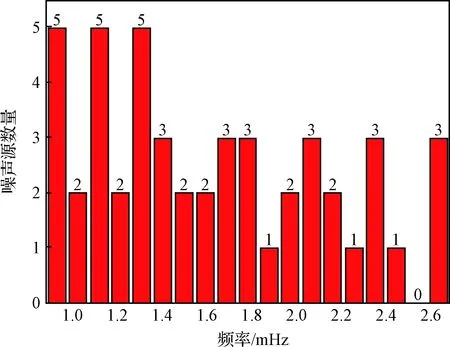
图19 电极笼频谱重叠Fig.19 Electric housing spectral overlap
在不同频点处,电极笼和周围环境的噪声频谱重叠个数不同,原因与光学基准板相同,而且随着频率的降低热噪声传播穿透力逐渐增强。选取低频段内两个典型的频点作频谱曲线,图20(a)频率为0.94 mHz,图20(b)频率为1.04 mHz,可以发现不同频段的热噪声在环境中的分布具有不均性。

图20 电极笼噪声源Fig.20 Electric housing noise sources
5 结 论
为满足太极二号卫星精密控温的需求,本文采用多级热阻尼控温方案,逐级降低环境热噪声。针对此方案,建立了多级阻尼状态空间数学模型,并且明晰了热扰动在复杂结构中的传递特性。为了验证多级热阻尼的防护效果,课题组开展了太极二号核心载荷舱专项热试验,结果满足指标要求,具体如下:
1) 在10~100 mHz频段内,光学基准板的温度稳定性≤13.6 μK·Hz-1/2,电极笼的温度稳定性≤11.5 μK·Hz-1/2,这表明太极二号卫星热控关键技术路线正确,并已完成试验验证;
2) 在1~100 mHz频段内,光学基准板的温度稳定性≤17.6 μK·Hz-1/2,电极笼的温度稳定性≤73.1 μK·Hz-1/2,距离太极三号卫星优于10 μK·Hz-1/2的控温目标仍有一些差距,需要在此基础上继续深入研究;
3) 通过噪声频谱分析,发现影响核心测量仪器温度稳定性的噪声源多集中在低频段,与环境噪声频段高度重合,这表明热噪声的传递机理与低频段热噪声的抑制方法,是后续提高控温精度的主要研究方向。
