柔性航天器预设性能及时间自抗扰姿轨跟踪控制

曹 芊，贾庆贤，李化义，马 晨，何文韬，张迎春

(1.哈尔滨工业大学航天学院，哈尔滨 150001；2.南京航空航天大学航天学院，南京 210016)

0 引 言

未来航天器在电子设备方面，如在电路、传感器和执行器的设计上愈加趋于大功率化的同时，也向着小型化发展。而传统的基于太阳能转换的动力子系统，即星载的太阳能阵列却不易实现小型化，反而在航天器电子设备的升级换代中越来越向大型化发展，这就导致阵列相对航天器整体的重量、体积和成本方面所占的比重越来越大，因此大功率卫星上的太阳能阵列一般具有非常长的翼展[1]。这种太阳翼一般具有较高的柔性和较低的固有频率[2]。目前的研究工作通常是进行地面或在轨测试以研究空间飞行过程中的太阳能阵列挠性动力学特性[3]。当太阳能阵列受到控制回路动力学或轨道机动加速度的激励，其产生的弹性振动可能会对整星动力学产生扰动，进而可能会影响到卫星的稳定[4]，因此有必要在姿轨控制器的设计中考虑太阳能阵列柔性的影响。

柔性航天器是典型的多体系统，一般由中心刚体和多个柔性附件组成。姿轨控制系统的设计需要考虑到中心刚体同各种柔性附件的耦合。近年来关于刚柔耦合航天器的研究主要集中于实现航天器姿态控制，对航天器轨道位置控制的研究较少[5-7]。文献[8-9]基于线性化的Newton-Euler方程提出了6自由度柔性航天器的线性化模型，并进一步实现了动力学模型的模块化构建[10]，大大简化了复杂多体机械系统的建模工作。

两航天器间的相对运动涉及姿态、轨道的变化，属于6自由度空间运动范畴，其有着两种不同的描述方法：一种称为向量代数法，文献[8]及文献[11]的模型构建均基于该方法；另一种称为几何力学法，又称螺旋理论，几何框架下描述的航天器运动往往具备更为简洁的形式，文献[12-13]在此框架下研究了不规则天体周围航天器的导航与控制，文献[14-17]依据此框架研究了航天器编队的控制及小行星周围航天器的悬停控制，文献[18]在此框架下设计了高精度的终端滑模姿轨控制器。

基于上述研究，为实现柔性航天器在预定时间、预设性能下的姿轨跟踪控制，本文首先推导了基于刚柔耦合多体航天器的相对耦合动力学模型并给出了预设性能约束后的相对姿轨运动学和动力学模型；然后设计了扰动观测器来估计振动引起的扰动力矩；最后设计了预定义时间积分滑模控制器对该模型进行一体化控制。通过Lyapunov理论证明了系统的闭环稳定性和跟踪误差收敛性。该算法通过对状态误差的实时监测来调整执行器的输出，使控制器在系统存在柔性振动及空间环境干扰的情况下仍可实现高精度的姿轨跟踪。仿真结果表明了该控制方案的有效性。

1 SE(3)上的运动学、动力学模型

本节在SE(3)框架下描述了处于任意位姿状态的刚性航天器、柔性航天器的动力学模型以及二者间的相对动力学模型。动力学模型的建立基于以下假设：

假设1.目标航天器在地球轨道上稳定运行，无控制力、力矩的输入；追踪航天器则存在控制指令的激励，因此本文中仅考虑追踪航天器的柔性，将目标航天器视为理想刚体。

1.1 数学基础及相关定义

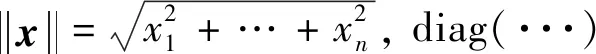
如图1所示，地球轨道上运行的航天器的位姿构型空间为李群SE(3)，其是航天器所有平移运动及旋转运动的集合，可表示为R3与旋转群SO(3)的半直积：

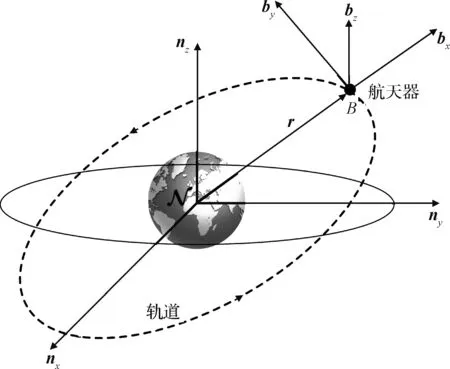
图1 惯性系下航天器的位姿表示Fig.1 Configuration of a spacecraft in the inertial frame

(1)

定义航天器角速度和线速度的一体化表示：速度旋量ξ(Twist)，力矩和力的一体化表示：力旋量φ(Wrench)，分别为：

(2)

式中：速度旋量和力旋量均定义在航天器体坐标系B中。

定义航天器的空间惯量矩阵：

(3)

式中：J,m分别为航天器的惯量矩阵和质量。

定义映射(·)∧:R3→so(3)，R6→se(3),(·)∧是SO(3)或SE(3)的李代数表达，其满足以下变换关系：

(4)

定义(·)∧的逆映射(·)∨:so(3)→R3,se(3)→R6。se(3)伴随矩阵可以表示为：

(5)

SE(3)伴随变换矩阵可以表示为：

(6)

1.2 运动学及动力学

考虑图2所示的单阵列柔性航天器，其中阵列坐标系P附着在阵列上，太阳能阵列相对中心刚体的位姿可由g0表示为：

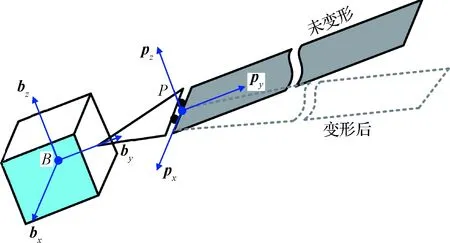
图2 考虑阵列柔性的航天器Fig.2 A spacecraft considering array flexibility

(7)

式中：lBP为P系在B系中的位置；RBP为P系相对于B系的旋转矩阵，其由阵列的倾角决定。

基于模块化的多体动力学建模方法，结合刚体旋量公式,B系下单阵列的柔性航天器的动力学可以表示为：

(8)

式中：φsc,B=φg+u+de，u为控制力项，φg为重力梯度项，de为环境干扰项；φhub/sa,B为B系中中心刚体施加于阵列的力旋量；Ihub为中心刚体的空间惯量矩阵。

阵列与中心刚体间的动力学耦合关系由模态有效质量方法描述[19]，耦合动力学依据悬臂模态模型描述[20]，阵列与中心刚体之间的连接为P系原点。则P系下阵列的动力学可以表述为：

(9)

式中：K为刚度矩阵；D为阻尼矩阵；η为模态位移列阵；L为阵列的模态有效质量因子矩阵，L∈RNm×6，Nm为模态截断的阶数。

式(9)中P系下描述的力旋量需要通过SE(3)伴随变换矩阵转换至B系。

(10)

通过式(10)的变换关系，将变换后的式(9)代入式(8)可得到追踪航天器的动力学方程：

(11)

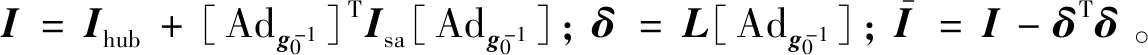
基于刚体假设的目标航天器动力学方程为：

(12)

式中：φg表示目标航天器的重力梯度项；ξt表示目标航天器的速度旋量。

上述重力梯度项φg的计算表达式为[21]：

φg=

(13)

式中：rB=RTr；r为惯性系至航天器体系B的标量距离;μ为地球引力参数。

航天器的位姿运动学方程可以表示为：

(14)

式(14)的一体化表示形式为：

(15)

式(15)的指数坐标形式方程为：

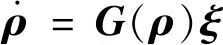
(16)

式中：指数坐标ρ=[ΘT,βT]T，其中Θ∈R3,β∈R3分别表示航天器姿态和位置的指数坐标，ρ可通过对数映射：exp(ρ∧)=g∈SE(3)→ρ∧∈se(3)和(·)∨映射获得，即ρ=(lng)∨。

G(ρ)的计算式如下[22]：

(17)

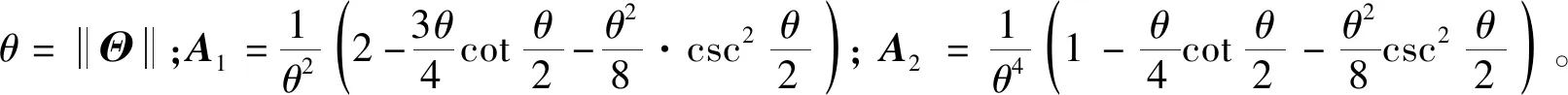
1.3 相对运动学及动力学

根据文献[16-17]，SE(3)上的相对运动学、动力学方程可表示为：

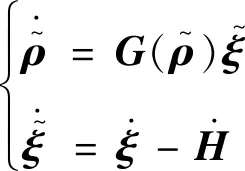
(18)

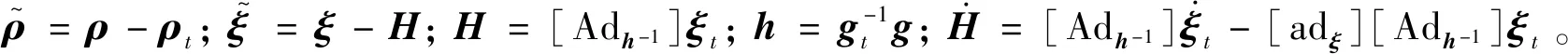
由式(11)和式(12)可推导出柔性航天器的相对运动学和动力学系统：

(19)

注 1.与航天器位姿及速度旋量参数相比，模态位移η的大小要小得多，但不可忽略；同时，由于模态变量的维数较大，因此分配在模态变量上的计算资源一般远大于位姿和速度旋量。当机载计算资源和存储空间有限时，关注其观测估计值比实时精确计算出模态位移更为现实有效。

注2.追踪航天器整个姿轨机动期间，在执行器作用下，不可避免会激发挠性结构的弹性振动，文中将弹性振动所产生的力旋量视为扰动项之一。

故式(19)可重述为：

(20)

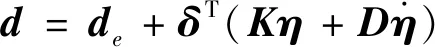
2 控制器设计

2.1 假设、引理

本节控制器的设计将基于以下假设、引理和定理：

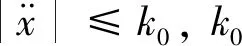
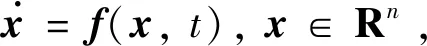
(21)

式中：q∈(0,1]。对于任意稳定解x0，稳定时间函数均满足：T(x0)≤T，则T为弱预定义时间。则称该系统是关于时刻T全局弱预定义时间稳定的。

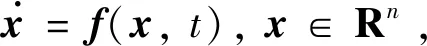
(22)

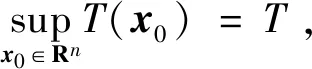
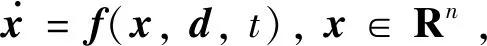
(23)

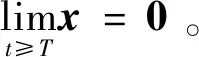
2.2 普通滑模控制器(SMC)

首先定义以下普通滑模面：

(24)

式中：s0=[s01,s02,s03,s04,s05,s06]T。

针对满足上述假设条件的航天器姿轨跟踪系统(20)，提出了本文的定理1。

定理 1.考虑式(20)的相对非线性系统，若满足假设1～3，采取如下控制律：

(25)

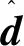
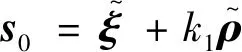
证.定义如下Lyapunov候选函数：

(26)

使用式(24)～(25)，对式(26)求导得：

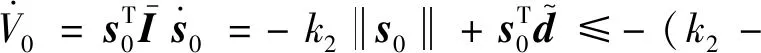
(27)

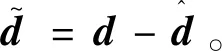
因此，当k2->0时，将是半负定的，则V0有界，因此位姿跟踪误差速度旋量跟踪误差有界。

对式(27)求导：

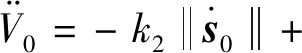
(28)

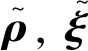
证毕。

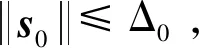
2.3 预定义时间扰动观测器

本节中扰动观测器用于估计姿轨跟踪系统中的集总扰动，基于文献[23]中的跟踪微分器及假设4，预定义时间干扰观测器(Predefined time disturbance observer,PTDO)可以设计为：

(29)

式中：α1,α2,α3,b1,b2为设计的观测器增益参数，b1tanhn(b2x)=[|x1|nb1tanh(b2x1),…,|xn|n·b1tanh(b2xn)]T。

根据文献[23]定理4.8及备注4.10，参数值α1,α2,α3与收敛时间相关，为保证式(29)中的观测器能够在预定义的时刻To前实现跟踪收敛，α1,α2,α3应该满足以下关系：

(30)

式中：γ>0;To为观测器收敛时间的上界；k0为非负的未知常数，可通过取较大的参数来满足。

注4.有关式(29)中预定义时间的跟踪微分器的稳定性证明可在文献[23]找到，本文不再赘述。

注5.与文献[23]不同，为避免计算过程中非连续性问题，文中将跟踪微分器中的符号函数sign用双曲正切函数tanh来进行替换，增益参数b1,b2取值越大，观测效果越好，但同时也会耗费较大的计算资源，实际应用中可根据观测误差要求及星载计算效率权衡取值。

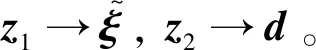
2.4 自抗扰预设性能及时间积分滑模控制器(ADR-PPT-ISMC)

为兼顾姿轨跟踪系统跟踪控制的动态性能，定义如下性能边界函数：

pi(t)=(pi0-pi∞)exp(-at)+pi∞

(31)

式中：pi(t)为随时间递减的性能函数，其中i对应各位姿自由度的预设性能函数；pi0为t=0时预设性能函数的取值；pi∞为t=+∞时预设性能函数的取值，i=1,2,…,6;a为跟踪误差的速率下界。

保证以下控制目标：

(32)

上述预设性能约束为不等式约束，为了简化控制律的设计，将不等式约束转换为等式约束，定义如下归一化跟踪误差：

(33)

选择光滑、严格单调递增的误差转换函数：

(34)

文中选取参数ϑi=1，则ftran(εi(t))=tanh(εi(t))。

利用误差转换函数对不等式约束进行处理：

(35)

ftran的逆函数可以表示为：

(36)

对式(36)求导：

(37)

通过上述定义及转换，得到以下预设性能约束后的姿轨运动学和动力学模型：

(38)

根据相关预定义时间控制理论，定义以下积分滑模面：

(39)

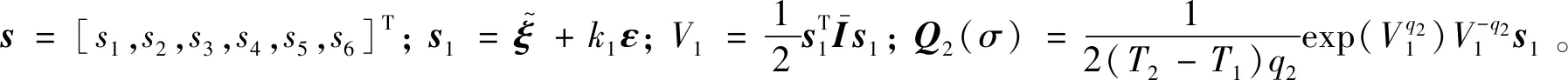
针对满足上述假设条件的航天器姿轨跟踪系统(38)，提出了本文的定理2。

定理 2.考虑式(38)的相对非线性系统，在假设1～4成立的前提下，若采取式(39)的滑模面，且控制律(40)设计如下：

(40)

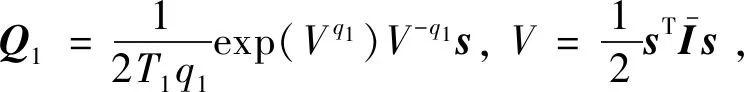
证.控制律(40)下的闭环系统可表示为：

(41)

(42)

对Lyapunov函数V求导，可得：

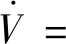
(43)

由假设3可知：

(44)

因此有：

(45)

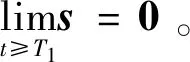
当t≥T2时子系统(41)满足以下关系：

(46)

因此根据引理2，系统(41)～(42)关于时间T2-T1是强预定义时间稳定的。但由于强预定义时间T1仅是滑模面收敛至s=0的最小上界，因此并不能确保时间T2为滑模面s1=0收敛时间的最小上界，因此根据引理1，系统(38)～(40)是关于时间T2弱预定义时间稳定的。

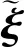
注8.控制器(40)，能够在预定时间T1内将跟踪误差驱动到定义的滑模面s=0，即跟踪误差在预定时间T1内到达滑模面(到达阶段)；后续可确保滑模运动在预定时间T2-T1时间内实现控制目标(姿轨跟踪误差收敛至零)并在其后保持，即保证滑动阶段的预定时间稳定性。其中T1为强预定义时间，T2为弱预定义时间。

3 仿真校验

为验证本文基于ADR-PPT-ISMC的柔性航天器姿轨跟踪控制器的跟踪性能，本节对上述提出的方法进行仿真验证。

设置仿真总时长60.0 s，时间步长0.1 s，地球引力参数μ=398600.44 km3/s2，两航天器的质量均为600 kg，惯量矩阵均为diag(110,100,115) kg·m2，其中追踪航天器太阳能阵列倾角30°，阵列坐标系P在体系B中的位置坐标列阵为[0,0.3,0]Tm，截取阵列的前3阶模态，阵列刚度矩阵为K=diag(8,15,20)，阵列阻尼矩阵为D=diag(0.05,0.05,0.05)，阵列的模态有效质量阵

观测器、控制律增益参数取值见表1，两航天器的初始状态见表2。

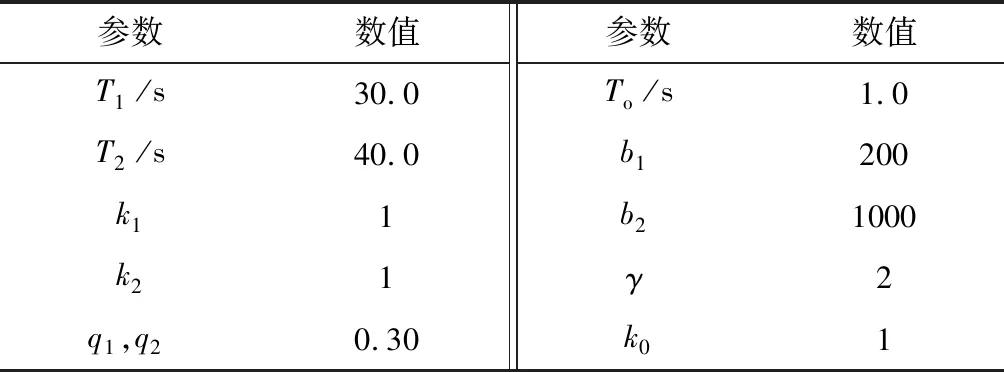
表1 控制器与观测器增益参数Table 1 Gain parameters of controllers and observers

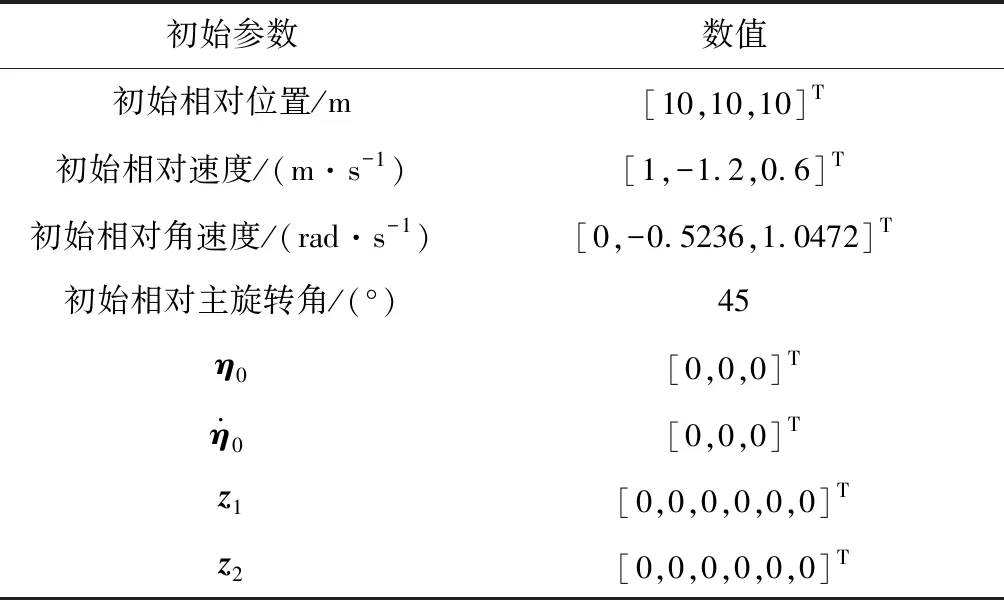
表2 初始状态Table 2 Initial states

两航天器相对姿态可由初始相对主旋转角及相对角速度确定。其中目标航天器的状态更新依赖于式(12)，其初始状态由一组低地球轨道参数给出，如表3所示。

表3 目标航天器的开普勒轨道参数Table 3 Keplerian orbit parameters of the target spacecraft

性能边界函数相关参数列阵如下：

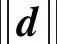
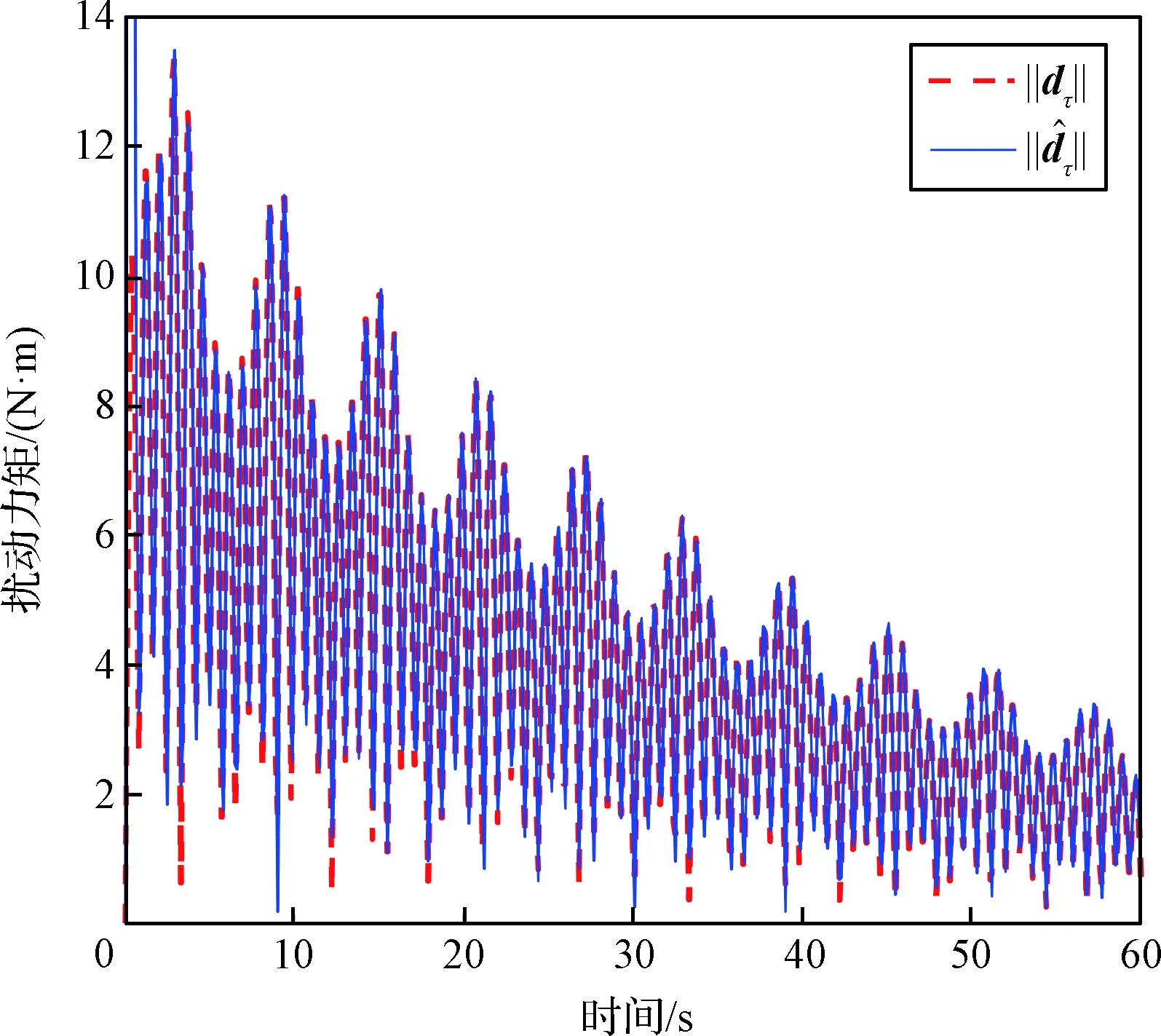
图3 集总扰动力矩的跟踪轨迹Fig.3 Tracking trajectories of lumped disturbance torque

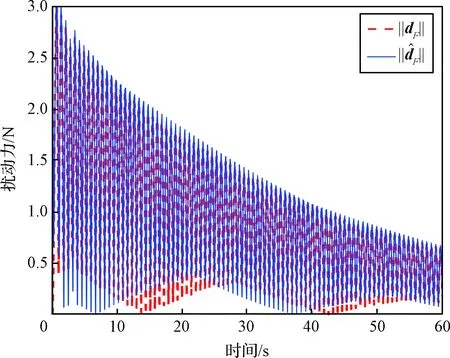
图4 集总扰动力的跟踪轨迹Fig.4 Tracking trajectories of lumped disturbance force

图5～图6为预设性能控制方法下的两航天器相对姿态和位置变化曲线，图7～8为无预设性能函数控制方法下的两航天器相对姿态和位置变化曲线。分别对比图5与图7，图6与图8，可以明显看出相对姿态与相对位置的超调量均有明显降低，此外由于性能函数(31)自身的衰减速度，使得系统整体的收敛速度也有所加快。文中性能函数(31)的作用主要在于改善系统的动态性能，尽管性能函数中也定义了误差界限以对系统的稳态性能提前界定，但系统的稳态性能主要还是依赖于文中所提出的ARC-PT-ISMC，因此为提高计算效率，pi∞的取值可适当放宽。

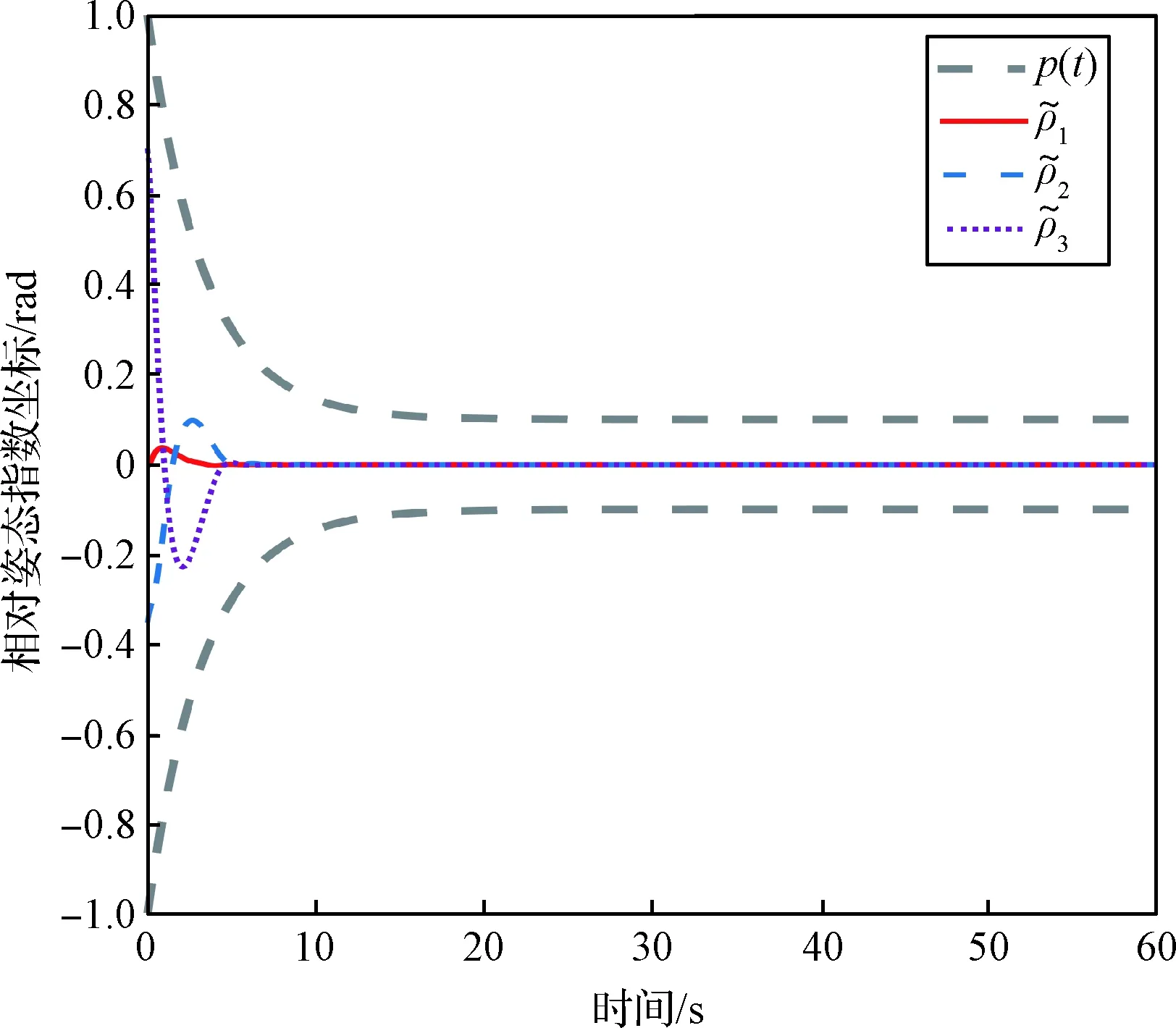
图5 相对姿态指数坐标的变化曲线(预定义性能)Fig.5 Variation of the relative attitude exponential coordinates (prescribed performance)

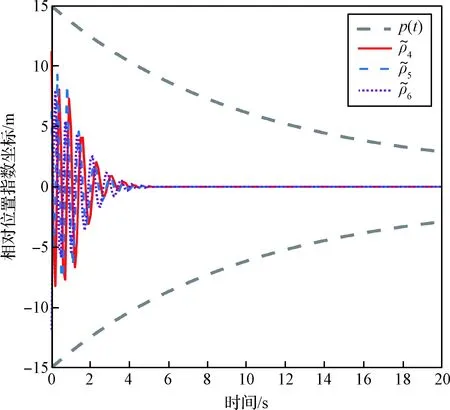
图6 相对位置指数坐标的变化曲线(预定义性能)Fig.6 Variation of the relative position exponential coordinates (prescribed performance)

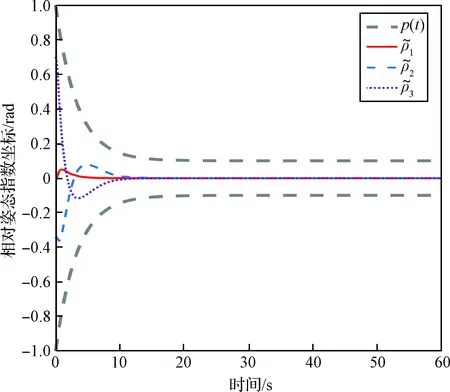
图7 相对姿态指数坐标的变化曲线(未预定义性能)Fig.7 Variation of the relative attitude exponential coordinates (unprescribed performance)

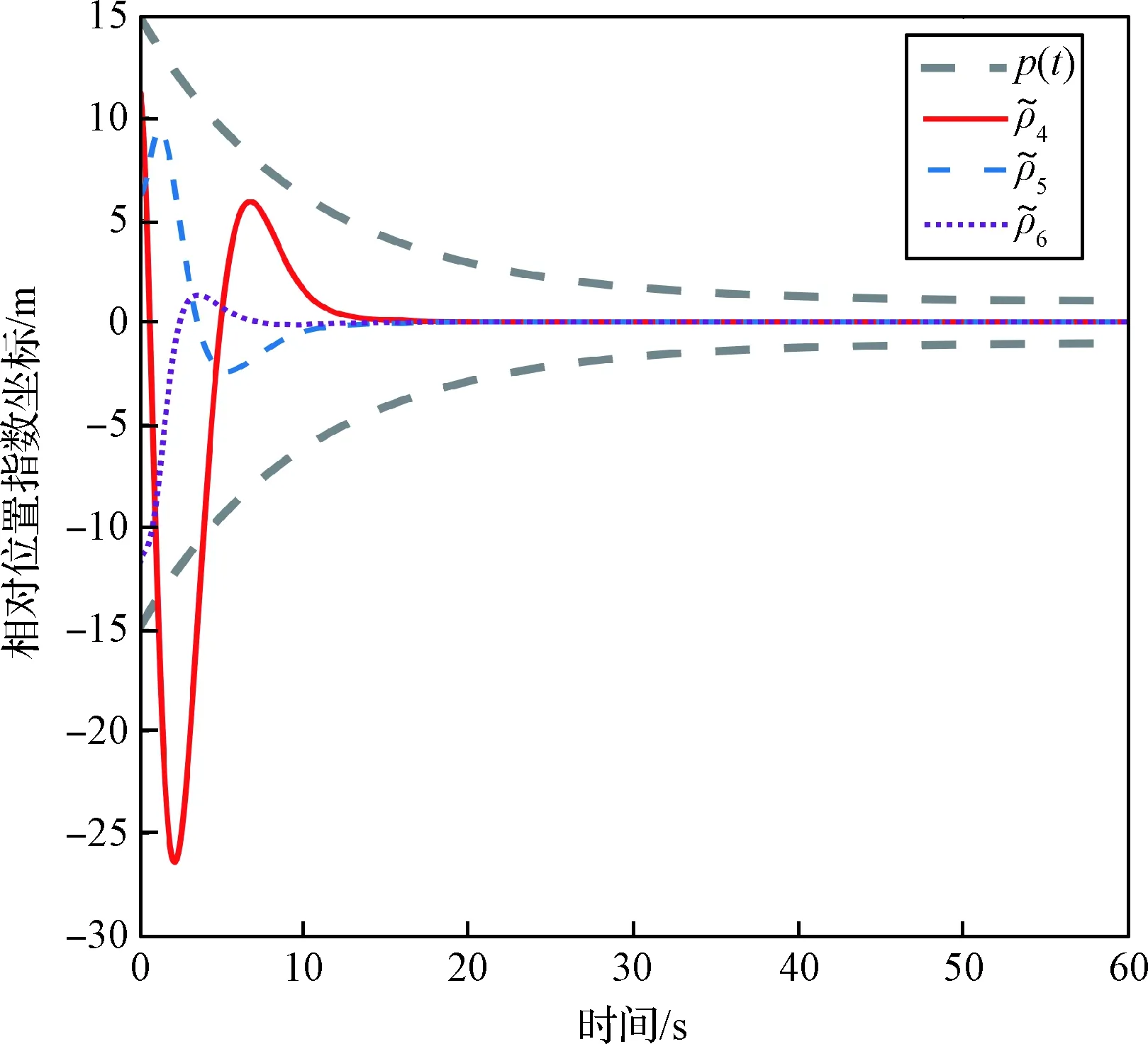
图8 相对位置指数坐标的变化曲线(未预定义性能)Fig.8 Variation of the relative position exponential coordinates (unprescribed performance)

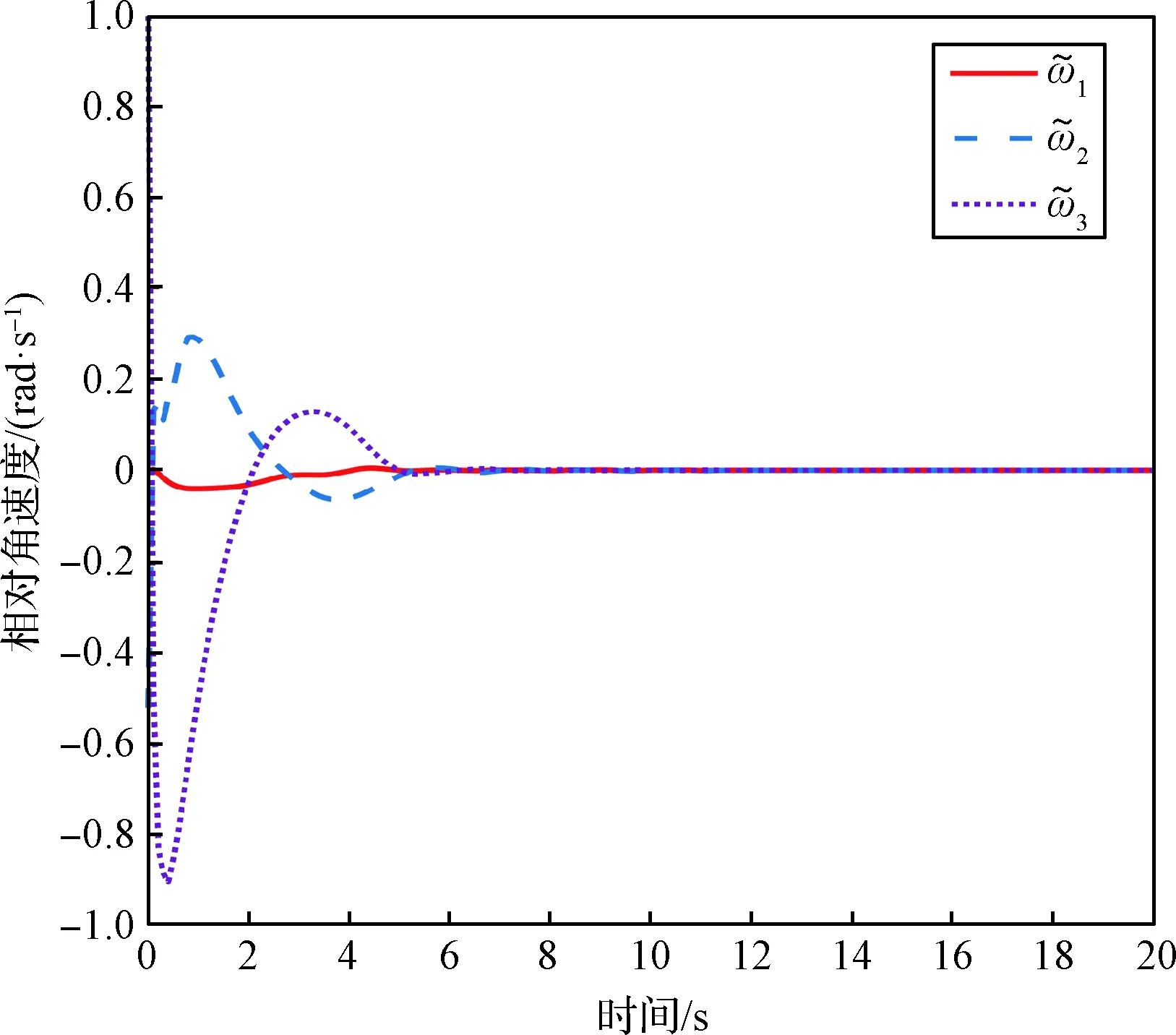
图9 相对角速度Fig.9 The relative angular velocity

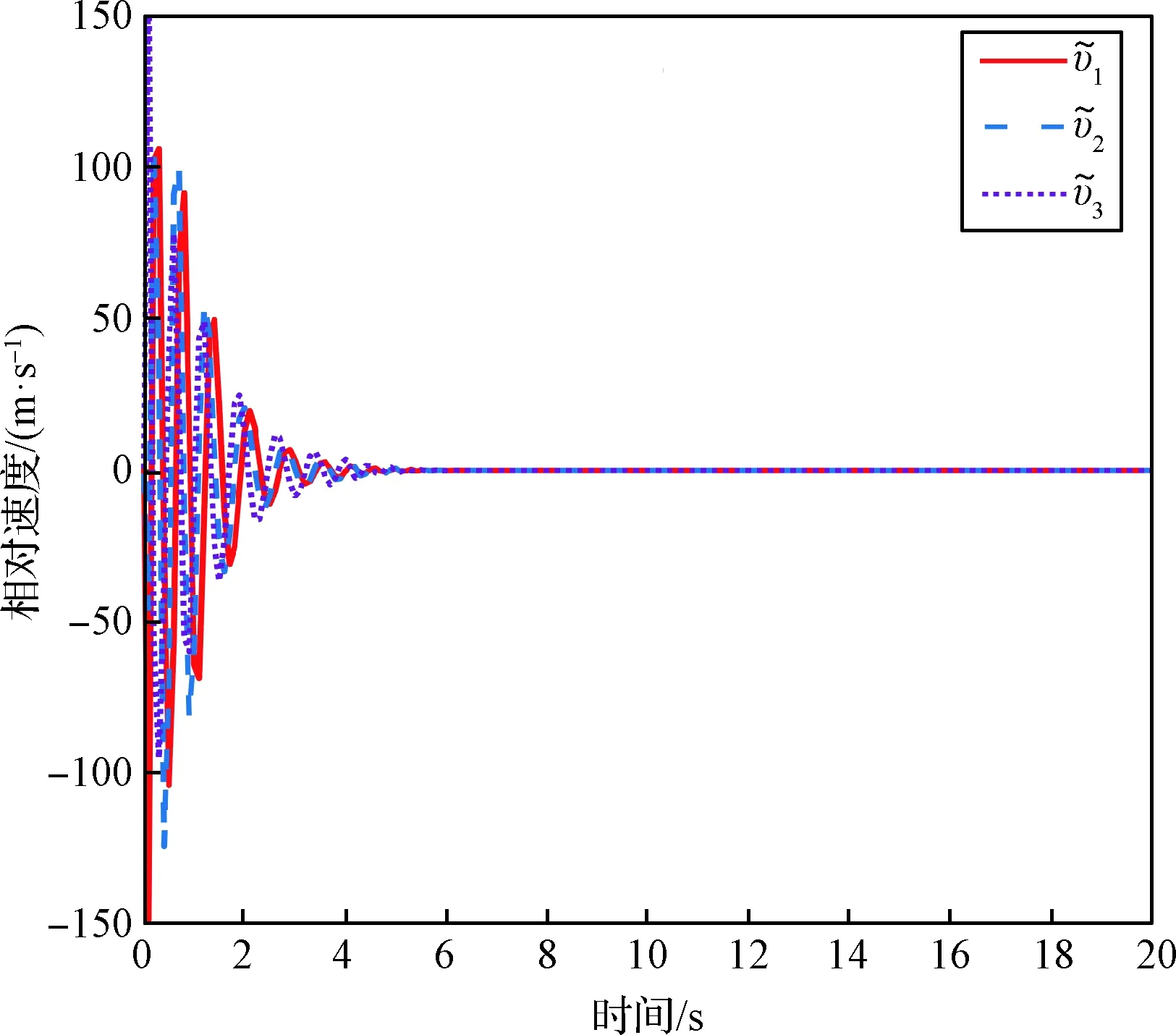
图10 相对速度Fig.10 The relative velocity

图11～12给出了集成自抗扰的复合控制方法(ADR-PPT-ISMC)和不考虑扰动控制方法(PPT-ISMC)作用下位姿指数坐标范数的变化情况。可以看出未使用ADR控制方案的姿态、位置误差范数受到系统扰动的影响，最终的指数坐标收敛误差分别收敛到10-4rad和5×10-5m，而该收敛误差精度要差于文中所提出的ADR-PPT-ISMC方法。上述分析表明，含ARC的复合控制方案的跟踪性能在收敛精度及抗干扰方面优于未使用ADR的控制方案。

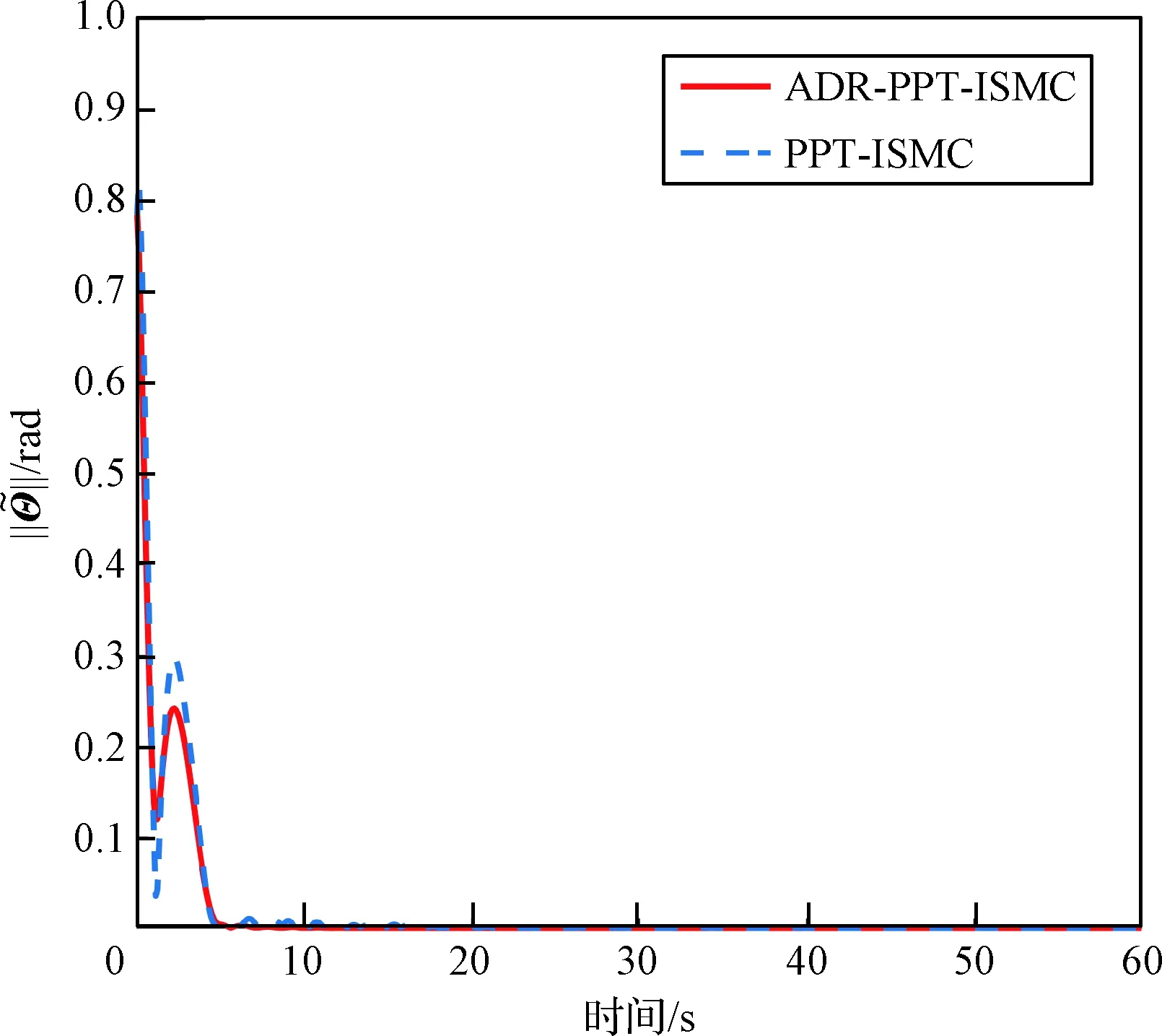
图11 相对姿态指数坐标的范数Fig.11 The norm of the relative attitude exponential coordinates

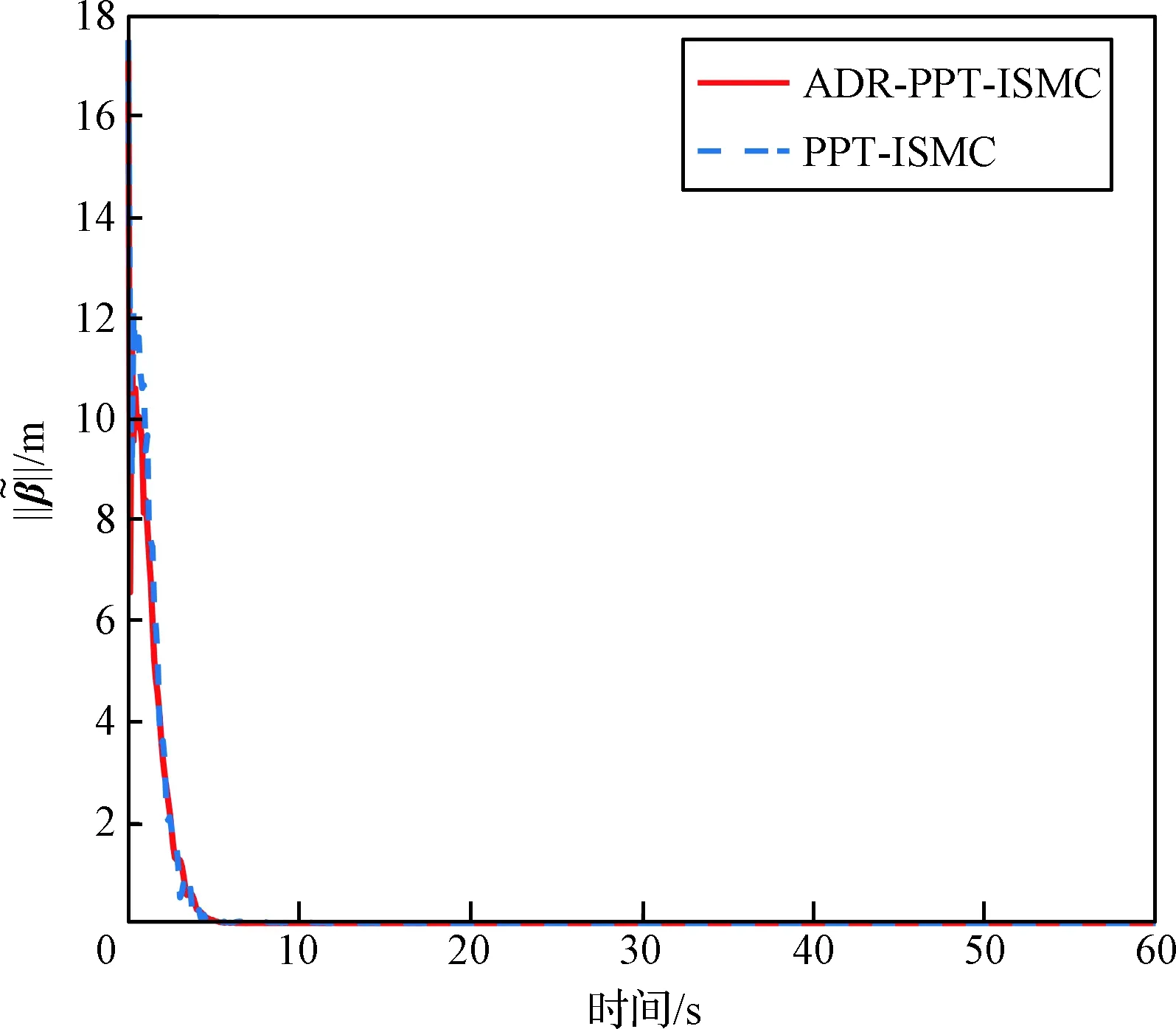
图12 相对位置指数坐标的范数Fig.12 The norm of the relative position exponential coordinates

4 结 论

对于考虑弹性振动及空间环境干扰下的柔性航天器姿轨跟踪问题，本文利用预定义时间稳定性理论给出一种预设性能及时间的自抗扰积分滑模鲁棒跟踪控制器设计方法，按照该方法设计的控制器，可以保证系统在预设性能参数及时间下渐近跟踪到预先设定的参考输入。采用预定义时间的扰动观测器以补偿弹性振动及外部干扰的影响,使其具有较好的鲁棒性。文中给出的仿真实例表明了该方法的有效性。