运载火箭推力故障不确定性下轨迹可达包络分析

李超兵，包为民，李忠奎，程晓明，魏才盛

(1.北京大学工学院，北京 100871；2.中国航天科技集团有限公司，北京 100048；3.北京航天自动控制研究所，北京 100854；4.中南大学自动化学院，长沙 410083)

0 引 言

运载火箭是执行航天任务的重要基础和保障。随着我国航天强国建设的步伐逐渐加快，对运载火箭的可靠性和智能化提出了更高的要求[1-2]。不同类型、不同级别的故障对任务的影响程度不同。动力系统故障是运载火箭最容易遭受到的故障，轻则导致火箭入轨精度降低，重则直接导致飞行任务的失败[3]。随着运载火箭在线计算能力的提高和火箭智能化相关技术的发展，当动力系统出现故障时，有望通过在线故障诊断和轨迹重规划，在线调整飞行程序，完成或部分完成既定任务。

近几年，许多学者面向推力故障下轨迹重规划问题开展研究。谭述君等[4]通过分别求解故障下面向目标轨道和救援轨道的离线重规划问题，构建了离线样本集，在线通过调用样本集完成实时轨迹重规划。马昊磊等[6]提出一种基于自适应伪谱法的故障火箭轨迹重规划方法。Li等[7]针对运载火箭突发电力故障问题，考虑规划方法的实时性，提出了一种基于凸优化的轨迹重规划方法。Song等[8]通过构造状态相关的评价指标，使得推力下降故障发生后，运载火箭能够自主决策和规划到目标轨道的轨迹。李远东等[9]针对可重复利用运载火箭的推力下降问题，提出了基于粒子群算法和优化ZEM/ZEV制导律的轨迹优化方案。Ma等[10]针对运载火箭突发的推力下降问题，提出了一种改进的并行牛顿制导算法，能够有效解决多约束下的制导问题。He等[11]基于凸优化方法和深度神经网络离线计算和构建故障状态到最优救援轨道的数据库，在线突发故障时可快速获得最优重规划救援轨道。Diao等[12]提出了推力故障运载火箭的在轨自主决策方法和基于目标自适应更新的迭代制导方法。值得注意的是，上述研究虽然能够针对特定故障，在线获得重规划的目标轨道或救援轨道，但并未考虑故障存在不确定性的实际工况。当运载火箭突发推力故障时，故障信息由故障诊断子系统估计获得，存在较强的不确定性。定量评估运载火箭推力故障不确定性的影响，分析不确定性下轨迹可达包络，对于推力故障下运载火箭的能力分析、在线自主决策和轨迹重规划具有重要的参考价值。

尽管对故障不确定性影响的研究较少，但已有部分研究开展了环境、测量、执行等环节不确定性的影响分析，对本文的研究具有重要参考价值。Luo等[13]综述了当前主流的不确定性影响分析方法，包含蒙特卡洛仿真法、局部线性化法、混沌多项式法、状态转移张量法、微分代数法等。Jones等[14]针对轨道不确定性的传播过程，基于混沌多项式法进行了求解。Valli等[15]基于微分代数法进行了不确定性的传播分析，以较小的计算代价实现了较高的估计精度。Yang等[16]考虑了航天器推力器的执行不确定性，基于状态转移张量法分析了不确定性对轨迹可达包络的影响。Jin等[17]面向航天器的交会问题，考虑了环境不确定性、测量不确定性、执行不确定性的影响，基于状态转移张量法构建了不确定性的传播和更新方程。在不确定性影响分析方法中，状态转移张量法由于不需要对不确定性进行随机采样[18]，因此非常适合用于推力故障运载火箭这类复杂动力学系统的不确定性分析。

本文针对突发推力故障的运载火箭轨迹重规划问题，考虑故障和环境存在不确定性，分析了运载火箭的轨迹可达包络。首先，建立了推力故障火箭轨迹重规划问题模型，并利用序列二次规划法进行求解。然后，通过对不确定性传播的建模，提出了基于状态转移张量法的运载火箭轨迹可达包络分析方法。最后，通过与传统蒙特卡洛仿真方法的对比，验证了本文方法的有效性和优势，有望为推力故障运载火箭的能力分析、自主决策和轨迹重规划提供技术支撑。

1 推力故障火箭运动模型与轨迹优化

运载火箭在地心惯性系下关于时间t的运动方程为：

(1)

式中：r为火箭位置矢量，v为火箭速度矢量，μ为万有引力常数，T为推力大小，u为推力单位矢量，m为运载火箭的当前质量，D为气动力矢量，g0为引力加速度，Isp为火箭发动机的比冲。

运载火箭上升过程中可能遭遇多类型故障。本文选择发生频率较高的推力下降故障进行分析。火箭发生推力下降故障后，真实推力大小为：

Treal=k0T

(2)

式中：k0为推力下降比例系数。

当运载火箭突发故障后，执行原定推力序列无法使火箭到达设计轨道的期望位置r(tf)和期望速度v(tf)，其中tf是入轨时间。为使推力故障对飞行任务的影响最小，需进行运载火箭轨迹的在线重规划。本文假设运载火箭在t0时刻突发故障，以燃料最省(到达设计轨道后火箭剩余质量最大)为优化目标，考虑动力学约束、起始与终端条件约束、推力约束等，建立如下推力故障火箭轨迹重规划问题模型：

(3)

式中：J为燃料最省性能指标，Re表示地球半径。

推力故障运载火箭的轨迹重规划问题可通过求解最优问题的一般方法，如序列二次规划[19]、凸优化[20]等方法进行求解，本文采用序列二次规划法对问题进行求解。

值得注意的是，轨迹重规划问题假设系统是完全已知的，忽略了环境不确定性(如气动不确定性)和故障不确定性对运动轨迹的影响。特别地，当发生推力下降故障后，火箭控制系统依赖故障诊断模块获得估计的推力下降比例系数k，当k存在估计不确定性时，小范围的推力大小变化将引起较大范围的轨迹波动，使得重规划轨迹失效。本文将基于状态转移张量法分析火箭轨迹优化受不确定性的影响，获得火箭轨迹的可达包络。

2 系统不确定性建模

包含不确定性因素下运载火箭的开环动态系统方程可以建模为：

(4)

E[w(t)wT(t′)]=Sw(t)δ(t-t′)

(5)

式中:δ(·)为Kroneckerδ函数，Sw(t)为相应的协方差矩阵。

系统的控制量输入依据导航状态计算得到，在该运载火箭的动力学模型中的物理意义为火箭推力，广义表达式为：

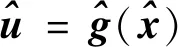
(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

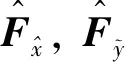
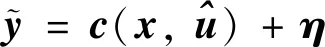
(15)

E[η(t)ηT(t′)]=Sη(t)δ(t-t′)

(16)

式中:Sη(t)为相应的协方差矩阵。

在突发推力故障工况下，虽然可以通过建立和求解在线重规划问题获得优化轨迹，但轨迹的重规划过程未考虑不确定性因素的影响。当发生推力下降故障后，火箭控制系统依赖故障诊断模块获得估计的推力下降比例系数k0,k0的估计值往往存在较强的不确定性。此外，大气密度ρ往往也存在不确定性，进而影响为气动力矢量D。最后，在故障发生时刻运载火箭所处位置状态也会存在一定不确定偏差，该偏差在运动过程中会随着时间累积而对运载火箭整体状态的计算产生一定影响。

为表示出系统动态方程(4)在考虑此类不确定性下的具体形式，需对系统的状态增广处理，也即定义运载火箭运动系统的真实状态为：

x=[rT,vT,cT,eT,dT,p]T

(17)

结合式(1)和式(4)，在考虑系统不确定因素作用下真实状态的动态方程具体可表示为：

(18)

(19)

vrel=(v+c)-ω×(r+e)

(20)

式中：Cd为阻力系数,Aref为参考面积，c∈R3,e∈R3,d∈R3和p∈R分别表示作用在遥测速度、遥测位置、推力加速度及大气密度上的不确定因素；ω×为地球自转角速度矢量ω的反对称矩阵。这些不确定性变量的动态过程满足一阶马尔克夫过程，即某时刻的状态只与上一时刻的状态有关。τc,τe,τd及τp分别对应偏差在整个系统中的时间常数。并且系统加入的不确定偏差满足高斯噪声的性质：

(21)

(22)

(23)

(24)

式中:σj(j=c,e,d,p)为对应不确定因素的稳定方差。

此外定义火箭运动系统的导航状态中包含火箭的位置、速度以及大气密度，具体为：

(25)

(26)

(27)

系统选择的测量状态为地心惯性系下的位置信息。也即：

(28)

至此建立了推力故障后运载火箭在不确定性因素作用下的系统状态动态方程。系统状态偏差的求解特别是运载火箭轨迹可达包络的求解还需对本章建立的不确定性模型作进一步处理。

3 运载火箭轨迹可达包络分析

(29)

(30)

(31)

(32)

式中：

(33)

(34)

(35)

同样地，对状态更新中的状态偏差量，即式(8)进行线性化可以得到：

(36)

(37)

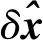
(38)

可以得到增广状态的状态方程为：

(39)

(40)

式中：

(41)

基于式(39)和(40)中给出的线性化后的系统状态方程，由状态转移张量法计算系统的线性协方差及其更新方程为：

CA=E[X(t)XT(t)]

(42)

(43)

(44)

考虑到系统状态在模型不确定因素作用下的误差传递状况可以通过系统真实状态的协方差矩阵来分析，因此提取协方差矩阵为：

(45)

基于系统状态偏差的协方差矩阵Dtrue，可以定量评估状态偏离期望状态的轨迹包络范围。

基于状态转移张量法的推力故障运载火箭轨迹可达包络分析算法如图1所示。从输入推力故障后重构的优化轨迹开始，在依据系统初始条件下确定的不确定性因素后建立对应状态偏差的协方差微分方程，最后利用数值计算的方法即可求解各个时刻下的状态偏差量。通过运载火箭状态与轨道位置的对应关系即可求出推力故障下不确定性作用的可达域包络。

图1 推力故障运载火箭轨迹可达包络分析算法Fig.1 Reachable envelope analysis algorithm for thrust fault launch vehicle trajectory

4 仿真校验

为验证本文提出的推力故障、气动以及位置信息等不确定下运载火箭轨迹可达包络分析方法的有效性,本节组织了两种不同推力故障及不确定因素作用下运载火箭轨迹包络优化计算算例，其中推力故障包括小推力故障损失以及较大的推力故障损失。运载火箭仿真相关参数如表1所示。

表1 运载火箭数据Table 1 Launch vehicle data

4.1 故障类型1计算仿真

故障类型1的仿真场景假定运载火箭在时间t0=200 s时突发推力下降故障，推力下降比例系数k0=70%，并且主要考虑推力及大气密度的不确定性因素。基于序列二次规划方法求解式(3)中推力故障火箭轨迹重规划问题，可获得故障后的重规划轨迹，如图2所示。重规划轨迹与标称轨迹的入轨轨道根数对比如表2所示。从图2和表2的仿真结果可以得出，入轨在t0=200 s发生推力损失30%，经过轨迹重规划，重规划轨迹终点的轨道根数尽管与标称轨迹的轨道根数存在一定的误差，但基本能够满足飞行任务的轨道要求。

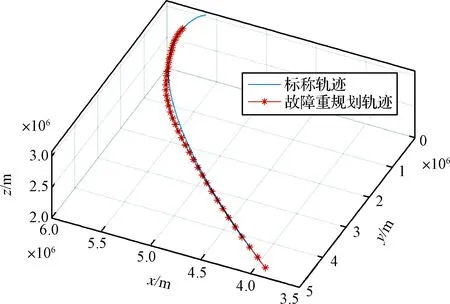
图2 故障类型1重规划轨迹与标称轨迹对比图Fig.2 Comparison between the replanning and nominal trajectories after fault type 1

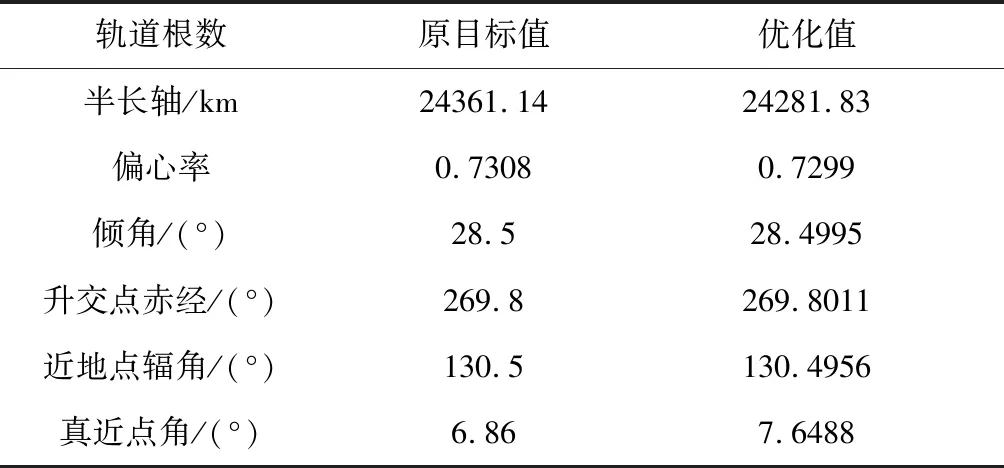
表2 重规划轨迹与标称轨迹入轨轨道根数对比Table 2 Terminal orbital elements comparison between the replanned trajectory and the nominal trajectory

为进一步分析故障发生后不确定性的影响，仿真中引入推力不确定性和气动不确定性，相关参数如表3所示。

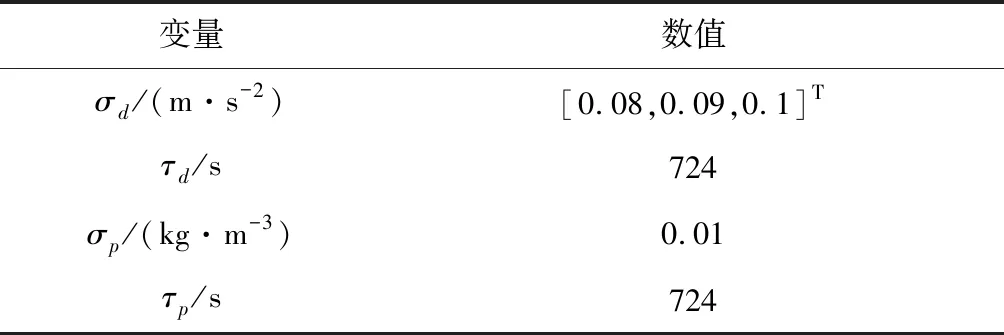
表3 故障类型1不确定性参数设置Table 3 Uncertainty parameter setting of fault type 1

基于本文提出的推力故障运载火箭轨迹可达包络算法，可以获得故障发生后运载火箭的状态偏移包络(3σ包络)，如图3到图5所示。其中图3给出了运载火箭位置矢量的包络分量，图4给出了运载火箭速度矢量的包络分量，图5给出了推力故障火箭重规划轨迹的局部轨迹偏差范围。

图3 运载火箭位置偏差随时间变化曲线Fig.3 Deviation curve of launch vehicle position with time

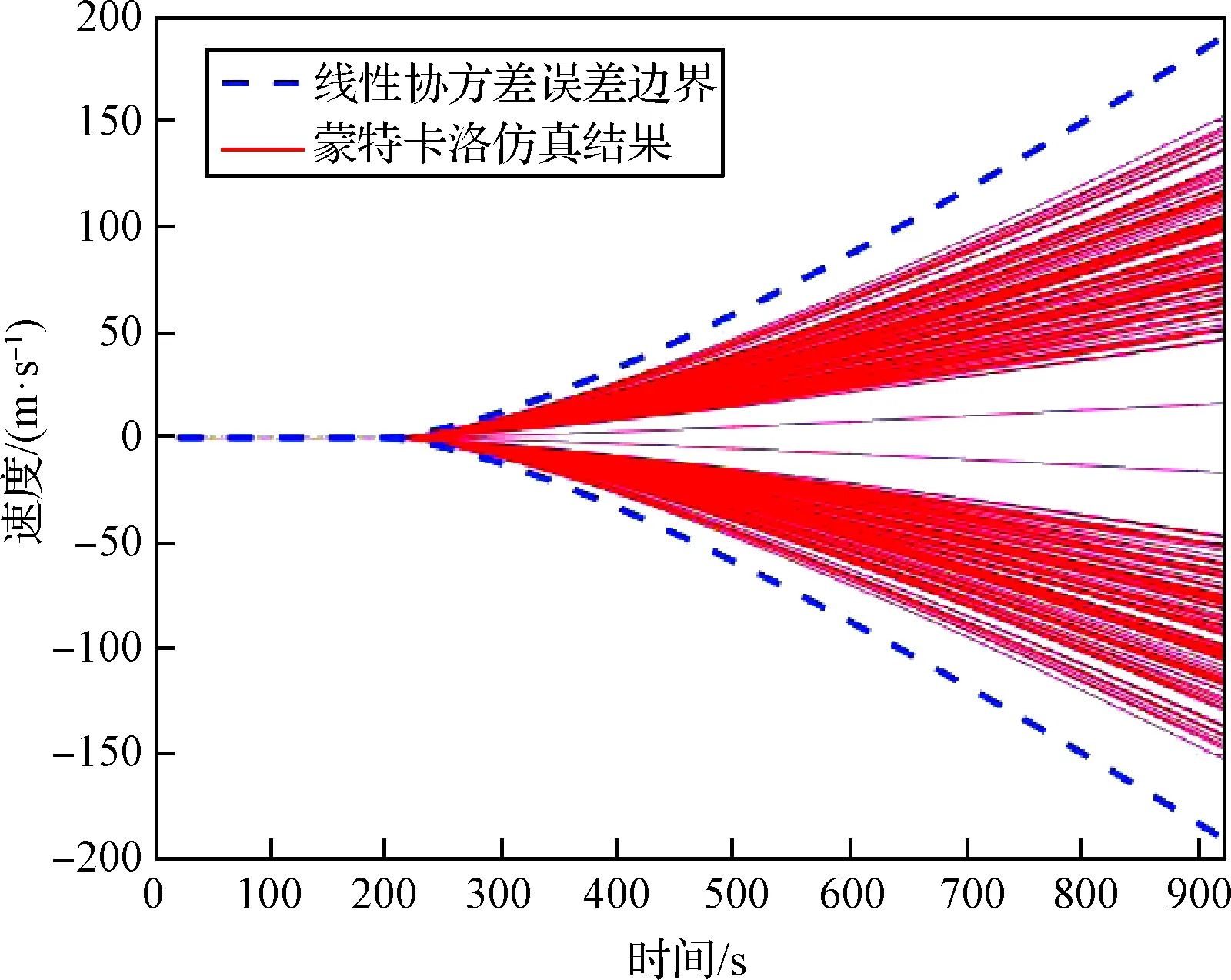
图4 运载火箭速度偏差随时间变化曲线Fig.4 Deviation curve of launch vehicle velocity with time

图5 推力故障火箭重规划轨迹的局部轨迹偏差示意图Fig.5 Schematic diagram of local trajectory deviation of rocket replanning trajectory with thrust fault

为验证所提方法的优势，本文基于表2中不确定性参数设置，随机进行了100次独立的蒙特卡洛仿真，仿真结果同样绘制于图3到图4中以方便进行对比分析。

结合该故障类型下的重规划结果以及计算出的火箭状态偏差量，为了能够更加直观地观察到系统状态偏离值对火箭终端入轨能力的影响程度，将状态偏差结果转换为火箭入轨时的轨道偏差，其偏差结果如表4所示。

表4 重规划轨迹入轨轨道根数偏差Table 4 Deviation of the terminal orbit elements in replanning trajectory

4.2 故障类型2计算仿真

在故障类型2的仿真场景中,假定运载火箭在时间t0=500 s时突发较大的推力下降故障，推力下降比例系数k0=50%，并且在考虑了推力及大气密度的不确定性外还加入了运载火箭故障位置不确定性因素。故障后的重规划轨迹如图6所示,重规划轨迹与标称轨迹的入轨轨道根数对比如表5所示。

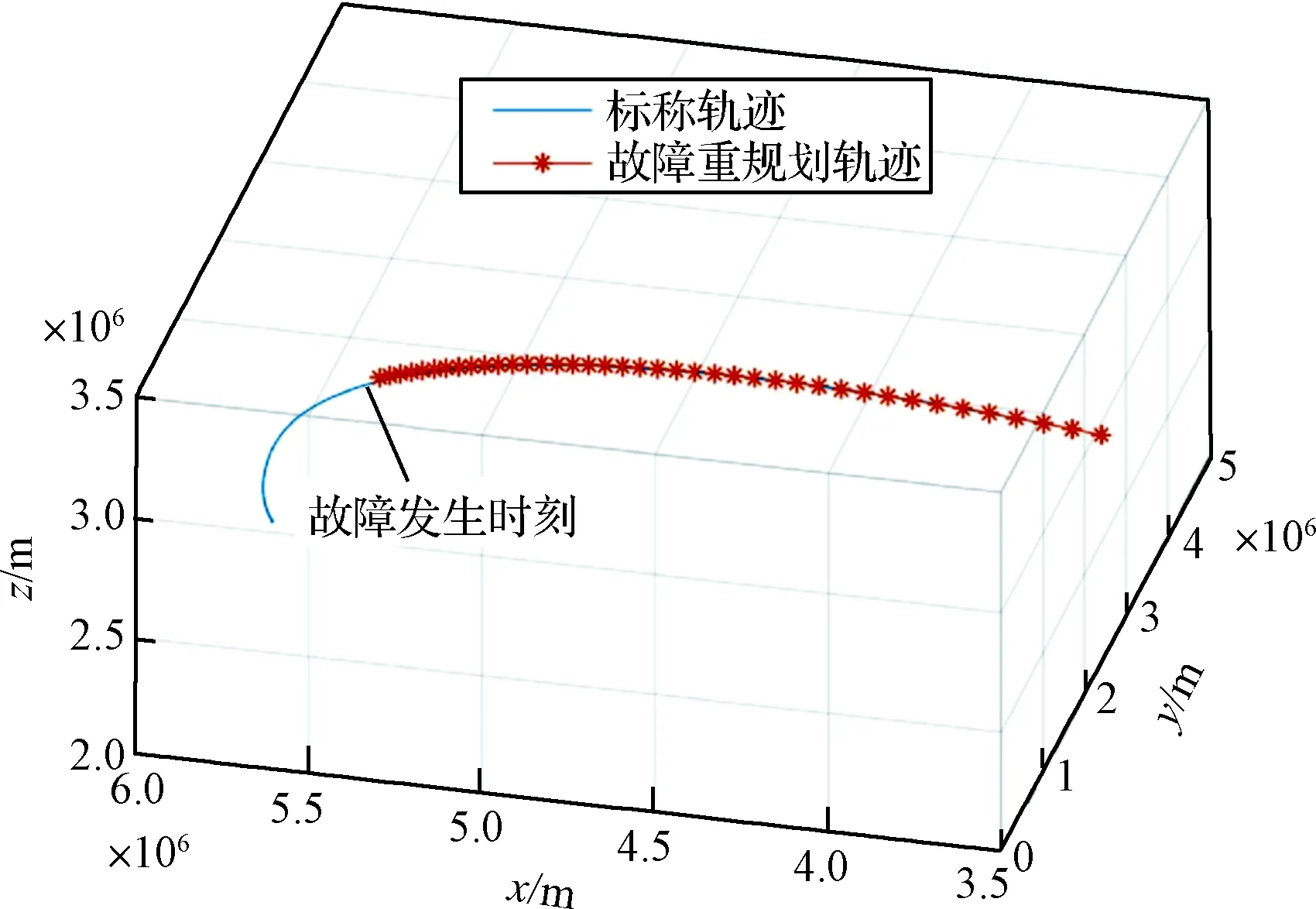
图6 故障类型2重规划轨迹与标称轨迹对比图Fig.6 Comparison between the replanning and nominal trajectories after fault type 2

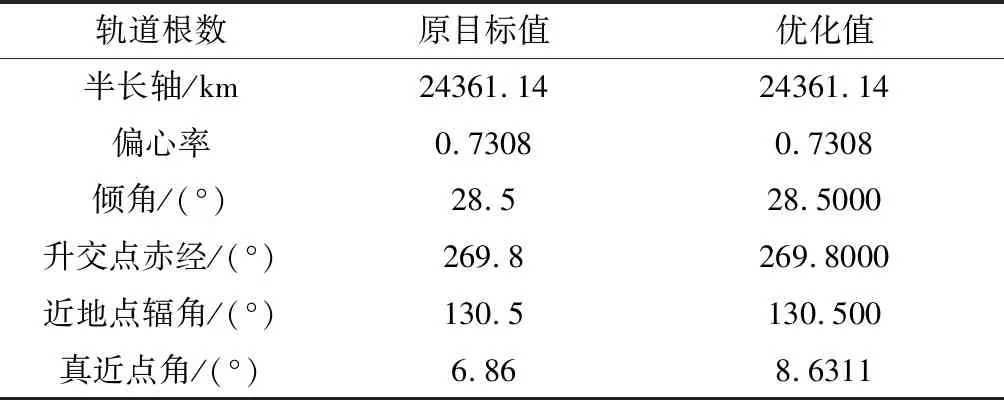
表5 重规划轨迹与标称轨迹入轨轨道根数对比Table 5 Terminal orbital elements comparison between the replanned trajectory and the nominal trajectory

在该故障类型中添加了额外的运载火箭火箭位置不确定偏差，各不确定性相关参数如表6所示。

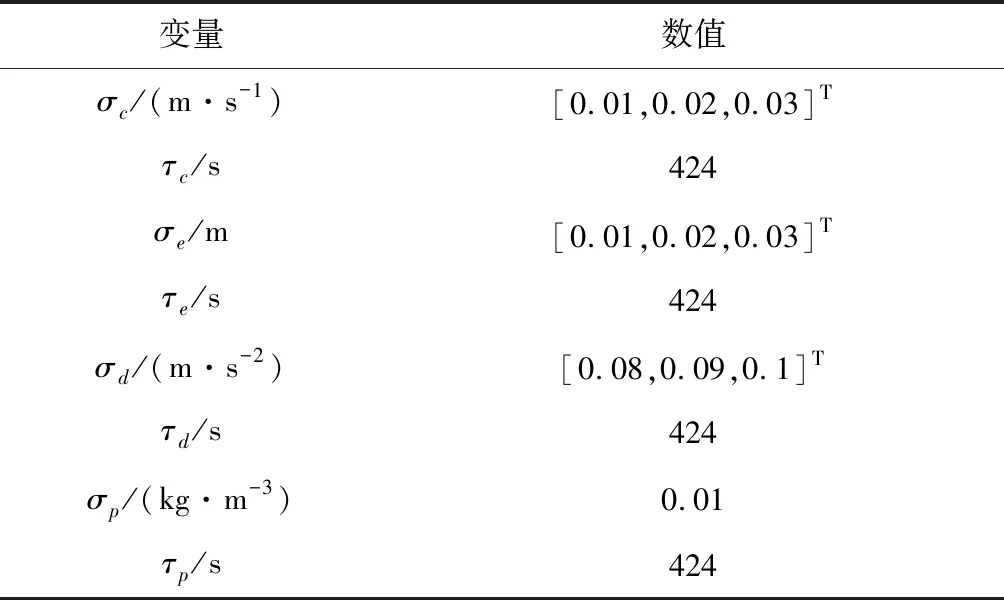
表6 故障类型2不确定性参数设置Table 6 Uncertainty parameter setting of fault type 2

在此故障类型下同样仿真计算出了运载火箭在位置和速度上各分量的偏差分布状况，计算仿真结果如图7-9所示。

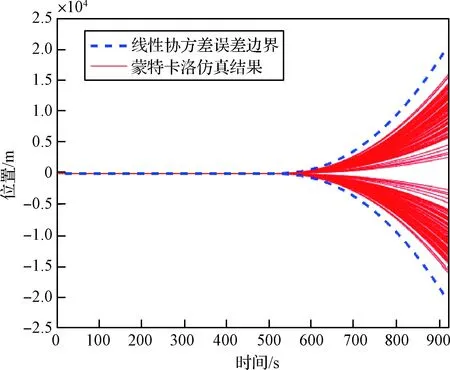
图7 运载火箭位置偏差随时间变化曲线Fig.7 Deviation curve of launch vehicle position with time

图8 运载火箭速度偏差随时间变化曲线Fig.8 Deviation curve of launch vehicle velocity with time

图9 推力故障火箭重规划轨迹的局部轨迹偏差示意图Fig.9 Schematic diagram of local trajectory deviation of rocket replanning trajectory with thrust fault

结合该故障类型下的重规划结果以及计算出的火箭状态偏差量，将状态偏差结果转换为火箭入轨时的轨道根数偏差，其偏差结果如表7所示。

表7 重规划轨迹入轨轨道根数偏差Table 7 Deviation of the terminal orbital elements in replanning trajectory

从以上2种故障类型的仿真计算结果中可以得出：本文提出的推力故障不确定性下运载火箭轨迹可达包络分析方法给出的位置矢量包络边界和速度矢量包络边界与100次蒙特卡洛仿真得到的偏差上界结果一致，验证了所提方法的有效性。区别于多次蒙特卡洛方法，本文方法能够一次性给出运载火箭轨迹可达包络，对于后续的运载火箭能力分析、故障发生后的决策等工作具有明确、直接、及时的参考价值。

5 结 论

针对突发推力故障的运载火箭的轨迹优化与设计问题，提出了一种基于状态转移张量法的故障火箭轨迹可达包络分析方法。通过建立推力下降故障的运载火箭运动模型，在不考虑不确定因素影响下，采用序列二次规划方法优化节求解出推力故障下的重规划轨迹。考虑故障和环境不确定性，基于线性协方差对非线性系统的传播过程进行建模和模型线性化，并采用状态转移张量法实现了对运载火箭轨迹可达包络分析。仿真结果表面，所提方法能够一次性给出运载火箭轨迹可达包络边界，与100次独立蒙特卡洛仿真得到的包络边界一致。论文所研方法有望为推力故障运载火箭的能力分析、自主决策和轨迹重规划提供技术支撑。