月壤钻采进尺力形成机理及进尺力预测建模
2023-02-28刘天喜
周 峻,刘天喜,梁 磊,赵 阳
(哈尔滨工业大学航天学院,哈尔滨 150001)
0 引 言
地外天体钻进采样是深空探测任务中极其重要的一项研究内容,其中,外螺旋内中空的取心方式是各国行星钻进机构的研发重点。此类结构能够较好地保持样品的层理特性,降低采样扰动,但是过于复杂的结构又导致了较高的故障风险。因此,为保障钻采设备能够高效可靠地完成采样任务,需要进一步开展机土相互作用机理、钻探工况识别、高度自适应无人自动控制等星球钻进采样技术的研究[1-2]。机土相互作用主要包括进尺力和回转扭矩两大部分,其中进尺力是指钻具与土体间发生切削、挤压、摩擦等作用从而在钻具轴向上产生的与进尺运动相反方向的合力,回转扭矩是指用于克服失效月壤对钻具发生阻力作用的周向扭矩,其形成机理是开展其他钻采技术研究的基础和关键,难点在于需要充分考虑月壤的特点,建立细观颗粒状态与宏观土体力学行为之间的跨尺度关联[3]。
嫦娥五号探测器发射前,对于钻采机土相互作用机理的研究主要关注点在钻头切削刃对土体的破坏作用,基于被动土压力理论,构建切削刃前的月壤失效区,通过失效区的受力和几何关系计算钻进负载[4-5]。而针对钻杆部分,文献[6]建立了钻杆螺旋槽内月壤运动模型,但目的是通过对钻杆几何结构参数与回转扭矩之间相互影响关系的分析实现钻杆结构设计的优化。以上模型与相关试验均聚焦于钻进回转扭矩的变化,然而进尺力作为保障钻进工况顺利完成的重要指标不应被忽略。文献[7]综合月壤回转切削作用下的剪胀模型、粮仓效应下的取心力学模型以及螺旋槽中钻屑的运移模型构建了基于特定钻进样本的自适应钻进策略,但是其采用的钻头形状并非探月工程中采用的双排阶梯构型,进尺力产生机理存在明显不同,忽略了钻头锥面贯入土体产生的挤压效应。近几年,钻进采样方面的研究多以离散元方法为主。针对月壤颗粒多孔多角的结构特点,建立可体现月壤大内摩擦角、小内聚力等力学特点的本构模型[8-10],对钻采过程中土体颗粒的运动场及应力场进行仿真[11-14],此外,还对钻进采样过程中岩石的影响[15]和样品分层的现象[16]进行了讨论。虽然离散元法契合了月壤的散体特性,能够在细观上为机土相互作用机理的研究提供支持,但是海量的颗粒运算导致仿真效率低下,无法支持月壤钻采状态的实时模拟与识别。然而,解析模型近年来进展缓慢,文献[17]基于细观上月壤颗粒的运动提出了一种基于试验数据的进尺力半经验预测模型,机土相互作用被简化为土体密度变化的映射,模型预测结果过于依赖试验样本,需要对进尺力的成因进行更深层次的分析。
综上所述,解析法近来无重大突破,现有成果均针对钻具结构设计优化,钻头形状与实际探月工程采用的双排阶梯构型存在明显差异,缺少对进尺力形成机理的探究;而离散元方法针对颗粒本构建模,关注钻进过程中的颗粒运动及现象,无法建立细观与宏观间的力学联系,且计算量巨大,耗时长,不利于后续开展月壤辨识反演等研究。因此,亟需在月壤钻采机土相互作用机理方面取得突破,为后续钻采过程中土体辨识、最优工况自适应控制等研究的开展提供可靠的理论支持。
基于以上问题,本文对钻采过程中土体随钻具运动产生的位移和形变进行分析,提出进尺力的形成机理,建立以钻头贯入回转状态土体柱孔扩张问题的等效解析解为核心的进尺力预测模型,开展模拟月壤地面钻采试验,并对模型进行验证。
1 进尺力形成机理
1.1 进尺运动分析
月壤钻采过程中,钻具的运动包含竖直方向的进尺运动和绕轴向的回转运动,与之接触的月壤随之运动并产生形变。由文献[17],月壤运动只发生在钻头附近的有限区域内,并且进尺力主要由钻头锥面贯入土体产生。为了进一步分析进尺力产生的机理,对钻具运动过程进行分解,并假设钻孔处样品土体均进入钻杆内部,不对钻具周围月壤产生影响,分析月壤产生的位移及变形情况,从而分析进尺力的形成机理。
图1为钻具进尺过程中土体位移示意图,t时刻钻具位置由实线表示,t+Δt时刻由虚线表示。当钻头向下移动Δh距离时,钻头周围月壤在径向被压缩Δr距离,两者之间存在如下关系:
Δr=Δh·tanθbit
(1)
式中:θbit为钻头倾角。
采用拉格朗日法对土体的变形进行描述,土体中任一物质点,如图1中A点,初始位置为r0,t时刻所在位置为A′,所产生的径向位移为ur(t)=r-r0,t+Δt时刻所在位置为A″,所产生的位移为ur(t+Δt)=r′-r0,两者之间存在如下关系:

图1 钻具进尺过程月壤位移示意图Fig.1 Displacement of lunar soil caused by drilling tool footage movement
(2)
式中:vz为钻具的进尺速度。
1.2 回转运动分析
图2为钻具回转过程中土体位移示意图,t时刻钻具位置由实线表示,t+Δt时刻由虚线表示。钻头侧边推动月壤运动,钻具以角速度ω匀速转动,则Δt时间内转过的角度为Δθ,那么土体中任一物质点转过的角度为uθ,如图2中的B点。转动时一侧土体受挤压,那么环向的位移必然是关于r和θ的函数。但是,钻具高速回转使土体被快速推动,环向的压缩形变远远小于空间上土体的位移,且钻头结构对称,因此,忽略环向的挤压变形,假设土体随钻具同样以角速度ω匀速转动。然而土体回转伴随排粉运动,因此,回转速度的快慢将影响四周土体的密度、孔隙率等属性。
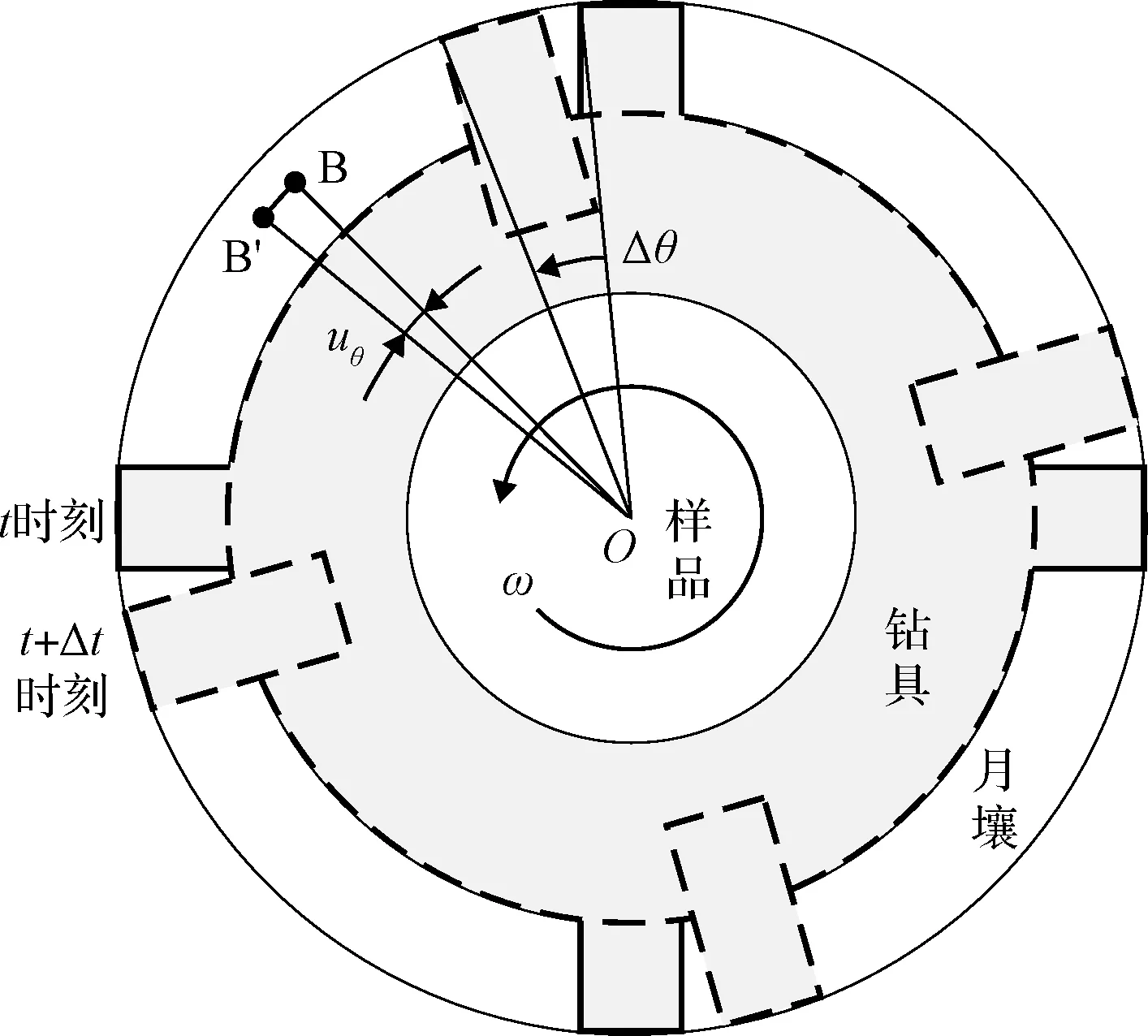
图2 钻具回转过程月壤位移示意图Fig.2 Displacement of lunar soil caused by drilling tool rotation movement
通过土体位移分析可知,进尺过程中,土体因钻头贯入在径向方向上产生压缩变形,从而产生径向压应力并作用给钻具。因此,进尺力实际为进尺过程中土体挤压钻具下移产生的摩擦力,包含钻杆处的摩擦力和钻头处竖直方向的摩擦力分量。回转运动并不直接与进尺力相关,但是会改变四周土体属性,影响钻具贯入产生的径向压力,进而影响进尺力的大小。
1.3 进尺力机理分析
如图3所示,假设深度为H的厚壁圆筒形土体是由竖直方向上n个高度为ΔH的相同尺寸的厚壁圆筒形土体叠加而成,每层土体初始内半径为a0,外半径为b0,由点划线表示。由于每层土体的高度ΔH极小,可将厚壁圆筒的形变问题等效为平面应变问题。钻头向下运动时钻头锥面贯入土体的过程即为每层土体平面从初始内半径扩张至接触部分钻具半径的过程,扩张后的土体尺寸由虚线表示。
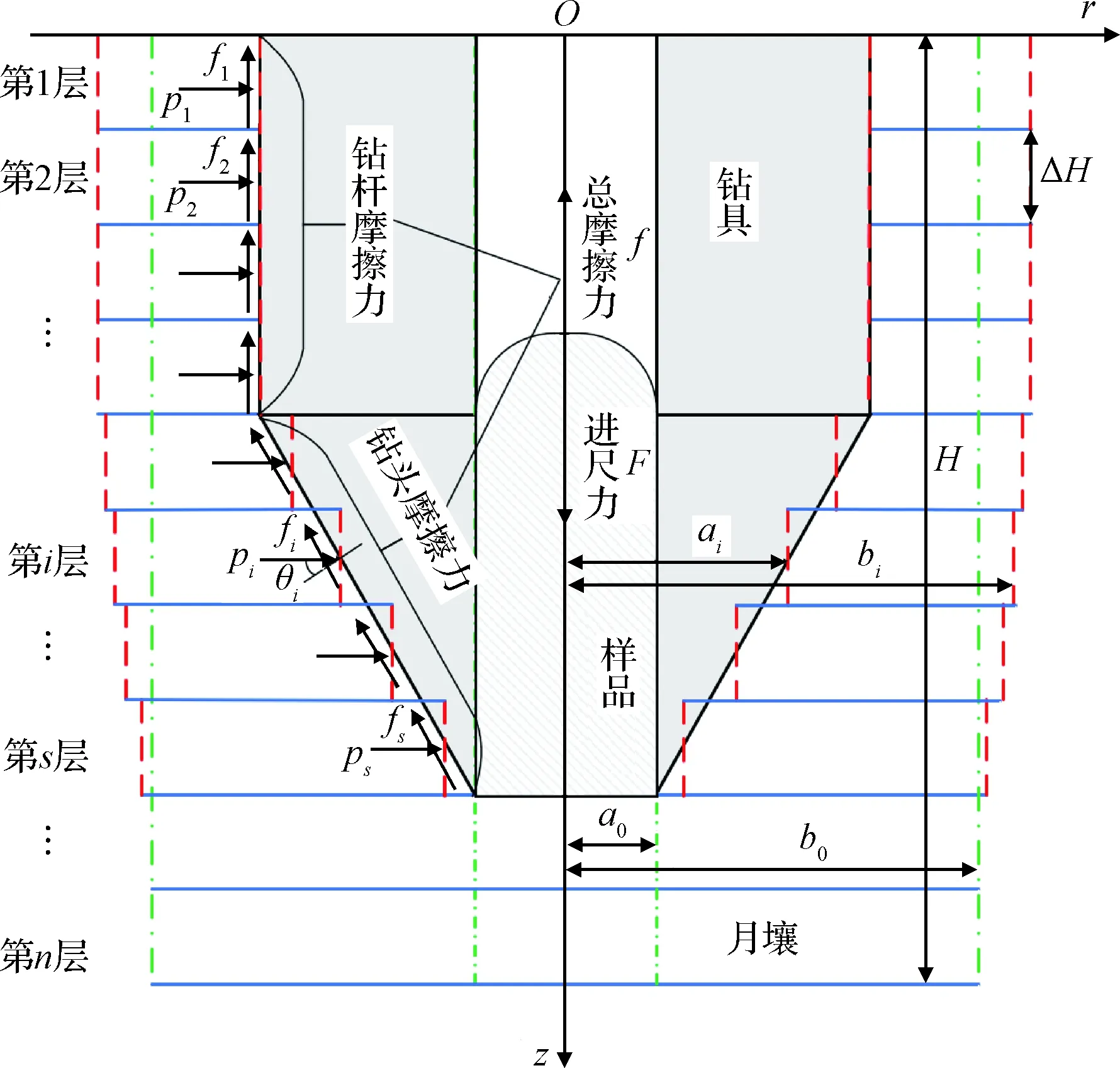
图3 钻具与月壤相互作用机理示意图Fig.3 Mechanism of the interaction between drilling tool and lunar soil
易得第i层厚壁圆筒土体对钻具产生的摩擦力fi为
(3)
式中:μ为土体与钻具间的摩擦系数;pi为第i层土体的孔壁压力;θi为pi与接触钻具表面法线的夹角,当处于钻头区域时,θi=θbit,当处于钻杆区域时,θi=0;dSi为第i层土体孔壁与钻具接触的面积单元;ai为第i层土体孔径;Δh为一层厚壁圆筒土体的高度。
进尺力F等于土体与钻具间的总摩擦力f,包括钻杆与钻头两部分,表示为
(4)
综上所述,进尺力的求解问题可转化为有限区域匀速回转土体的柱孔扩张问题,即求解孔径扩张至ai时的孔壁压力pi。
2 进尺力预测模型
由进尺力的形成机理可知,进尺力预测模型的核心是求解每一层厚壁圆筒土体在当前时刻所处扩张状态下的孔壁压力。土体随初始内孔径a0的增大发生变形,该变形按发展顺序最多可经历三个阶段,分别为弹性阶段、弹塑性阶段以及完全塑性阶段。设厚壁圆筒土体是均匀且各向同性的,密度为ρ,并以恒定的角速度ω绕轴线转动。
2.1 弹性阶段
土体形状为厚壁圆筒,故采用极坐标系进行分析。平面内任一点位置可通过坐标(r,θ)描述,可得回转状态下单位土体的平衡微分方程为
(5)
式中:σr为径向正应力;σθ为环向正应力;ρω2r为单位土体被施加的离心惯性力。
土体的弹性应力-应变关系在平面应变问题中表示为
(6)
式中:εr为径向线应变;εθ为环向线应变;ur为径向位移;E为土体的弹性模量;ν为土体的泊松比。
边界条件可通过孔径a处和外壁b处的载荷得到,为计算方便,将载荷分为静压力和回转附加压力两部分,表示为
(7)
式中:p为扩孔压力;p0为初始压力;k1为回转附加压力系数,记为k1=(1+2ν)/(8-8ν)。
由式(5)至式(7)解得,土体发生弹性变形时的应力分布函数为
(8)
位移分布函数为
(9)

2.2 弹塑性阶段
随着孔径a的逐渐扩大,土体变形加重,孔壁最先达到屈服条件。采用库伦-摩尔屈服准则[18],可得屈服状态下径向正应力与环向正应力间的关系为
(10)
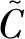
令
(11)
则屈服准则可表示为
ασθ-σr=Y
(12)
当式(8)中的r=a时,将应力结果代入式(12)中,可得孔壁处恰好达到屈服状态的极限孔壁压力pmax1为
(13)
为使后续推导简洁明了,将上式中的回转项系数记为k2=[2ν(α-1)+α+3]/(8-8ν)。
此后,随着孔径的扩张,土体变形将分为塑性区和弹性区两部分,如图4所示。设弹塑性区边界的半径为c,该边界所对应的物质点初始位置为c0。边界内的塑性区土体单元满足平衡微分方程式(5)和屈服准则式(12),化简得塑性区应力分布微分方程为
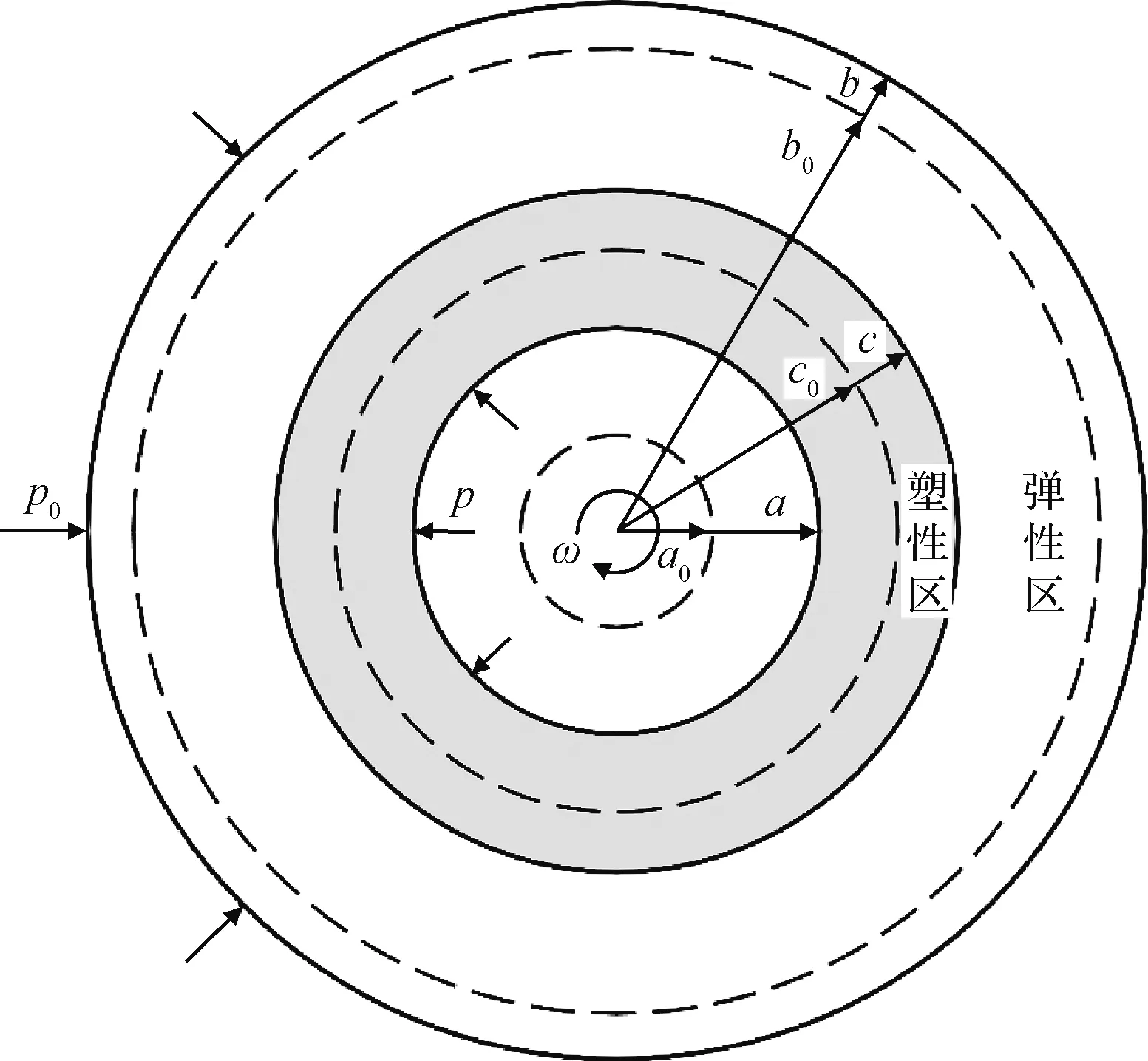
图4 弹塑性阶段柱孔扩张示意图Fig.4 Cavity expansion of cylindrical finite rotation soil in elastoplastic stage
(14)
解得塑性区应力分布函数为
(15)
式中:D1为第一个积分常数。
弹性区应力分布函数可根据弹性区微分平衡方程、应力应变关系以及r=b处的边界条件解得:
(16)
式中:D2为第二个积分常数。
因应力分布具有连续性,所以令r=c,联立式(15)和式(16),可确定两个积分常数分别为
(17)
(18)
那么,由式(15)当r=a时,可得孔径与弹塑性区边界之间的关系为
(19)
虽然得到了塑性区的应力分布函数,但是由于当前弹塑性区边界c未知,不能对应力分布情况进行求解,因此,需要对扩孔过程中土体单元的位移情况进行分析。
易得弹性区的位移分布为
(20)
当式(20)中的r=b时,可得到土体外边界的位移,为
(21)
土体发生塑性屈服所产生的形变可分解为弹性应变分量和塑性应变分量两部分,用上标el和pl分别表示。对于非关联的库伦摩尔流动法则,径向塑性应变分量和环向塑性应变分量存在如下关系:
(22)
式中:ψ为土体的剪胀角。
将弹性阶段的应力应变关系式(6)代入塑性流动法则式(22)中,可得塑性区应力应变为
(23)
将式(23)进行积分,以孔壁恰好进入屈服状态时弹性应力应变的解和孔壁压力pmax1作为初始条件,化简得到屈服阶段应力应变关系式为
(24)
式中:Q是积分常数,其表达式为
(25)
针对塑性阶段的土体大变形问题,采用对数应变对土体位移与应变之间的关系进行描述:
(26)
将式(15)、式(17)以及式(26)代入式(24)中,化简后得:
(27)

(28)
其中,κ1,κ2,κ3以及κ4是与土体状态相关的常量,其表达式为
(29)
采用换元法对式(27)进行求解,令:
(30)
将式(27)化简为
(31)
式中:系数γ=[α(1+β)]/[(α-1)β]。
在区间[r,c]上进行积分即可得到塑性区内的位移分布函数:
(32)
对于弹塑性区边界处,土体位移同样具备连续性,因此通过弹性区位移关系式(20)可得边界处的位移关系为
(33)
为了对式(32)中的积分进行数值计算,引入无穷级数进行等效,即:
(34)
式中:j为无穷级数的阶数。那么,当r0=a0,r=a时,即可得到塑性区的孔径扩张关系为
(35)
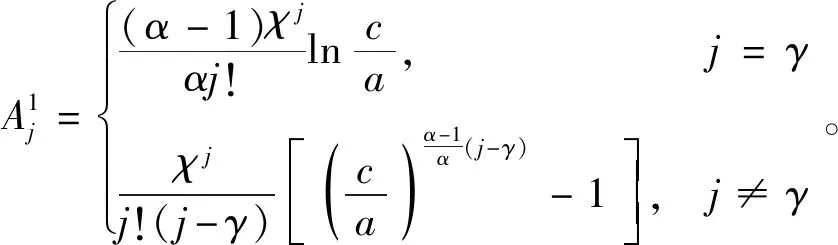
2.3 完全塑性阶段
弹塑性区边界随孔径扩张而随之外移,当与土体外边界重合时,即c=b时,土体完全进入塑性状态,由式(19)可得,此刻孔壁压力p与当前土体内外径之比存在如下关系:
(36)
塑性区的应力应变关系式(24)是基于塑性流动法则建立的,因此,土体进入完全塑性状态后仍然满足该关系。对式(31)在区间[r,b]上进行积分即可得到位移分布函数为:
(37)
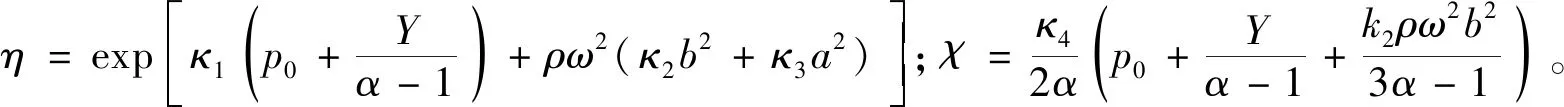
同理,采用无穷级数进行等效,当r0=a0,r=a时,即可得到完全塑性阶段的孔径扩张关系为:
(38)

综上所述,求解进尺力时,首先需要判断当前孔径下土体处于的变形阶段,采用对应公式解得土体的位移分布情况,进而求得孔壁压力,最终将各层土体的孔壁压力代入式(4),即可得到当前时刻的进尺力。
3 试验验证与分析
3.1 钻进试验
采用土壤综合试验平台进行模拟月壤钻采试验,钻具为双排8齿阶梯构型,如图5所示,钻具尺寸如表1所示。

图5 双排8齿阶梯构型钻具Fig.5 A drilling tool with double rows and eight-tooth ladder configuration

表1 钻具尺寸参数Table 1 Drilling tool size parameters
采用文献[17]中的基础模拟月壤作为试验对象,土体密度经测量为1.65 g/cm3。试验的进尺速度为90 mm/min,匹配低、中、高三种回转速度(60 r/min,90 r/min,120 r/min)形成三种仿真工况,如表2所示。模拟钻进采样100 mm,并实时采集钻进过程中的进尺力数据。

表2 各试验工况的钻进规程Table 2 Drilling procedures for various test conditions
3.2 仿真算例
根据文献[11]以及模拟月壤制备指标以及试验测量数据,设置仿真中的土体材料属性和尺寸参数,如表3所示。

表3 仿真设置参数Table 3 Simulation parameters
钻具尺寸设置与试验采用的钻具尺寸一致。对于低、中、高三种回转工况,分别设置相应的运动内聚力为1.5 kPa,1 kPa,0.5 kPa。仿真钻进距离为100 mm,并将土体在竖直方向上平均分成1000层,对钻进过程中每层土体孔壁压力和进尺力进行求解。
以钻头从开始进入到完全穿过第500层土体为例,该层土体钻孔扩张时的孔壁压力曲线如图6所示。钻头进入土体后,土体迅速进入弹塑性阶段,此阶段的孔壁压力呈快速增大趋势,并很快达到极值,孔径仅扩张了5%左右。此后,土体进入完全屈服阶段,此阶段孔壁压力随孔径扩张而逐渐减小,明显表现出土体的剪胀特性。对于低、中、高速三个回转工况,第500层土体的孔径由7 mm分别扩张至7.3664 mm,7.2872 mm以及7.2395 mm时,孔壁压力达到极值,即回转速度越快土体孔壁压力达到极值所需要扩张的程度越小,土体越容易进入完全塑性阶段。
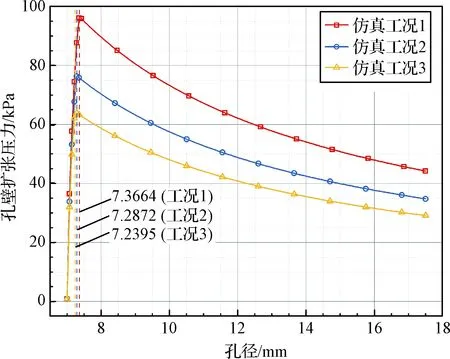
图6 第500层土体钻孔扩张孔壁压力曲线Fig.6 Borehole wall pressure of the 500th layer soil with cavity expansion
3.3 试验结果对比分析
图7中虚线和实线分别表示试验采集的进尺力结果和仿真预测的进尺力结果。通过对比可知,本文提出的模型能够较为准确反映钻采过程中进尺力的变化趋势。在钻头入土阶段,进尺力较小,且变化缓慢;钻头完全钻入土体后,进尺力快速增大,且进尺力增量随钻进深度的增加而增大。此外,回转速度增大时,进尺力及其增量均随之减小,体现了土体回转速度增大后土颗粒流动性增强从而内聚力减小的特性。
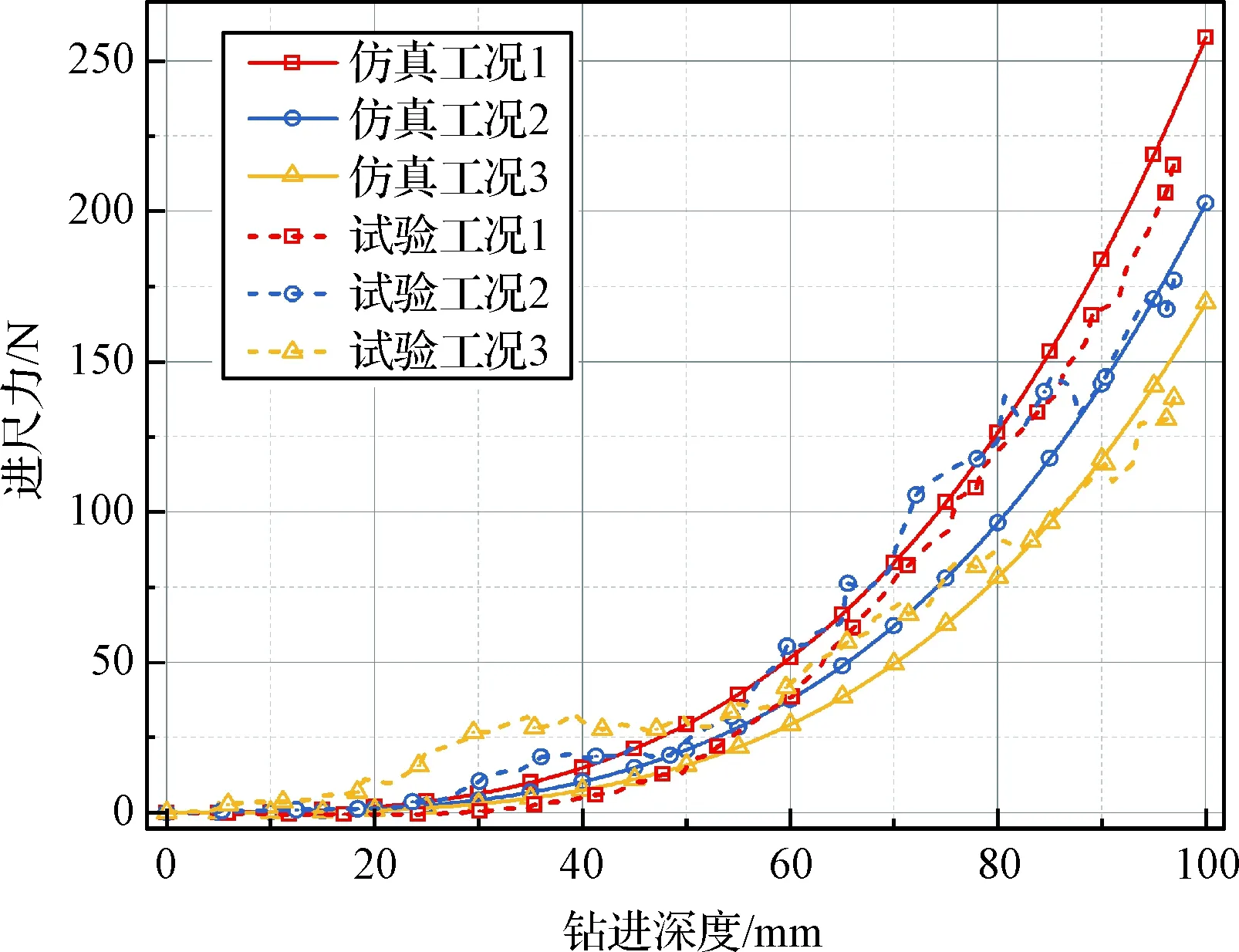
图7 模型计算结果与地面试验结果对比Fig.7 Comparison of simulation results with ground test results
4 结 论
本文通过钻采过程中土体运动和形变分析了进尺力形成机理,得到了回转状态下土体柱孔扩张问题的等效解析解,并以此建立了钻采进尺力预测模型,通过模拟月壤钻采试验验证了模型的正确性,并得到如下结论:
1) 本文详细分析了钻具进尺和回转两种运动模式下土体的位移和形变,得到进尺力的形成机理,进尺力即为钻具下移过程中钻具表面的总摩擦力,其值与土体向四周扩张而产生的径向压力有关。
2) 求解了回转状态下有限土体柱孔扩张问题的等效解析解,得到了弹性阶段、弹塑性阶段以及完全塑性阶段土体的应力和位移分布函数,并建立了钻采进尺力预测模型。
3) 进行了模拟月壤钻采试验,经过试验与仿真结果的对比,模型能够准确预测钻采过程中的进尺力,验证了模型的合理性,为钻采技术的机理研究提供可靠的理论支持。
