隧道循环进尺的极限平衡分析*

梁桥 杨小礼 陈翔

(1.中南大学 土木工程学院, 湖南 长沙 410075; 2.湖南工程学院 建筑工程学院, 湖南 湘潭 411104;3.湖南湘平路桥建设有限公司, 湖南 长沙 410075)

隧道循环进尺的极限平衡分析*

梁桥1,2杨小礼1陈翔3

(1.中南大学 土木工程学院, 湖南 长沙 410075; 2.湖南工程学院 建筑工程学院, 湖南 湘潭 411104;3.湖南湘平路桥建设有限公司, 湖南 长沙 410075)

为使隧道施工中开挖进尺的选择更加合理,提出了掌子面超前核心土对数螺旋破坏模式,该模式由拱顶围岩与超前核心土两部分组成;针对拱顶围岩,基于Janssen筒仓理论和Mohr-Coulomb强度准则建立了竖向力计算公式,而针对掌子面超前核心土,基于对数螺旋破坏模式推导了循环进尺计算公式,建立了循环进尺与内摩擦角、黏聚力、支护压力、开挖高度等参数之间的相互关系.研究结果表明:在施工阶段考虑隧道掌子面稳定性时,必须考虑循环进尺的影响,掌子面附近围岩状态的短期改变会使掌子面超前核心土所需的支护力比未考虑循环进尺的情形急剧增长;黏聚力与内摩擦角的改善对循环进尺与掌子面区域稳定性具有重要的意义,而支护力对该区域的影响具有临界性,不可盲目增大.

循环进尺;极限平衡;对数螺旋;破坏模式;超前核心土

隧道施工时,掌子面周边围岩平衡被打破,施工中初支、衬砌安装滞后,为保证隧道稳定,并充分发挥围岩自承能力,需在隧道开挖过程中选择一个合适的开挖进尺.一般而言,循环进尺过小,会使得造价提高、工期延长,支护增加;循环进尺过大,易使拱顶不稳定甚至塌方[1].因此,根据不同地质条件、施工工艺等合理选择开挖进尺是隧道施工的难点之一.Anagnostou等[2]的研究表明,掌子面附近不仅有横向拱效应,而且有纵向拱效应;Lee等[3]对不同循环进尺条件下掌子面的稳定性进行了缩尺模型试验研究和分析,证实掌子面的稳定性受循环进尺的影响较大;文献[4- 5]从普氏平衡拱理论和太沙基松散介质理论出发,对隧道循环进尺进行了推导和计算.可见,对于隧道循环进尺问题,国内外学者均已开展了相关研究[6- 7],但研究成果相对较少,理论依据依然较缺乏,给实际工程中循环进尺的选择带来不便与困惑.

文中基于Janssen筒仓理论和Mohr-Coulomb强度准则,考虑了掌子面前方超前核心土极限平衡与掌子面周边整体稳定性[8],推导了循环进尺计算公式,并结合实例进行了分析.

1 循环进尺的计算模型

当隧道埋置深度达到一定限值时,围岩具有成拱作用,其围岩压力仅是隧道周边某一范围内围岩的重力,而与埋深无关.基于Janssen筒仓理论的掌子面稳定性分析模型如图1所示[1].图中，M为三角形楔形体所受水平摩擦力，V为竖向力，σn为掌子面均布支护力，θ为三角形楔形体斜边与水平面的夹角.

图1 基于Janssen筒仓理论的掌子面稳定性分析模型

Fig.1 Stability analysis model of tunnel face based on Jan-ssen’s silo theory

基于文献[3,9]模型试验(如图2所示)与文献[8,10- 11]的掌子面对数螺旋破坏模式,在考虑掌子面前方及上部荷载效应的基础上建立了如图3所示的考虑循环进尺的掌子面稳定性计算模式.

图2 掌子面与循环进尺1∶40模型试验[9]

Fig.2 Model tests of the tunnel face and round length in 1∶40

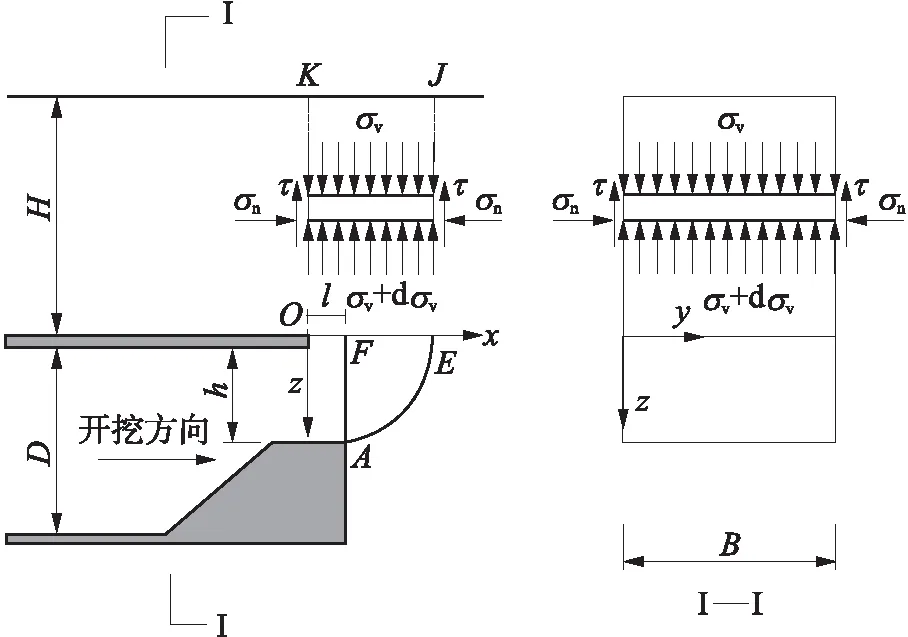
图3 掌子面拱顶围岩破坏模式

该破坏模式由上部OEKJ方形体与下部AFE对数螺旋体组成[10],该模式与Lee等[9]模型试验结果形态相似.在该模式中,剪切强度在方形体、对数螺旋体四周作用,这部分剪切强度对保持掌子面的平衡具有积极的意义.当上部结构产生的作用力与下部对数螺旋体能维持平衡时,掌子面稳定,否则掌子面破坏.

在图3中,取隧道宽度为B,隧道高为D,隧道开挖高度为h,埋深为H,循环进尺为l,则拱顶对数螺旋曲线AE方程为[11]

r=r0exp(θtanφ)

(1)

在常规的钻爆法施工时,常常采用台阶法施工,即选取开挖高度h=D/2,此时螺旋半径OE为

(2)

式中，θa为初始∠AOF.

当不考虑地表荷载时,取上部结构单元体列竖向平衡方程:

(3)

(4)

将式(2)、(4)代入式(3),积分可得作用在FE上的竖向力Fsilo为

(5)

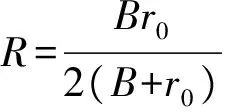
由式(5)可知,上部结构体所产生的竖向力随着埋深H的增加而增加,但当埋深H趋于无穷时,竖向力将为恒值,即作用在掌子面前方土体的竖向力随着埋深的增加而趋于恒定,这有利于确定隧道掌子面的支护压力上限.

为使整个破坏模式维持平衡,需求解对数螺旋体AFE所能提供的最大竖向力, 因此取对数螺线体中某一微单元斜面列平衡方程[17],如图5所示,通过微分方程求得允许作用在FE面上的最大竖向力F.

图4 掌子面超前核心土对数螺旋体破坏模式

Fig.4Logarithmicspiralfailuremodeoftunnelfaceadvancedcoresoil

图5 微单元受力分析示意图

Fig.5 Schematic diagram of force analysis for an infinitesi-mal slice

螺旋曲线方程采用的是极坐标,为求得螺旋曲线上某点在直角坐标系中的斜率,通过坐标变换得

(6)

求得螺旋曲线上某点在x-z坐标系中的斜率为

(7)

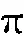
在微单元体斜面的切向与法向求平衡方程,其中切向平衡方程为

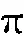
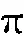
(8)

法向平衡方程为

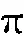
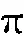
(9)

微单元体的重力

dG=γBdA

(10)

其中dA为微单元体侧面积,即

dA=(rcosθ-l)dz

(11)

作用在微单元体上的支护力

dp=σBdz

(12)

其中σ为作用在掌子面的支护力.

(13)

式中,dN为斜面法向力.

同理,在微单元体侧面的剪切力为

dTs=2dA(c+σytanφ)

(14)

式中,σy为侧压力强度,

(15)

竖向力强度为

(16)

将式(16)、(15)、(11)代入式(14),得

(17)

将式(17)、(10)、(12)、(13)代入式(8)、(9),联立方程求解得

(18)

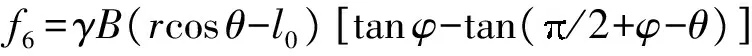
当掌子面与循环进尺区域维持平衡时,微分方程求解需满足以下条件:当θ→θa时,F→0,即拱脚位置能保持原有平衡;当θ→0时,F→Fsilo,掌子面前方土体能维持拱顶的平衡.

当l=0时,该破坏模式退化为只考虑掌子面稳定而未考虑循环进尺影响的情况,这方面的研究成果较多,式(18)结果与其他研究成果的比较如图6所示,其中文献[18]采用黏聚力c=5 kPa进行数值计算,文献[19- 20]选取砂土进行试验,文献[20]认为其黏聚力为0～5 kPa.从图中可知,当不考虑循环进尺时,本文结果与数值、试验结果较为接近,都在c=5 kPa左右,且具有相似的趋势性规律,可见该式具有一定的合理性.

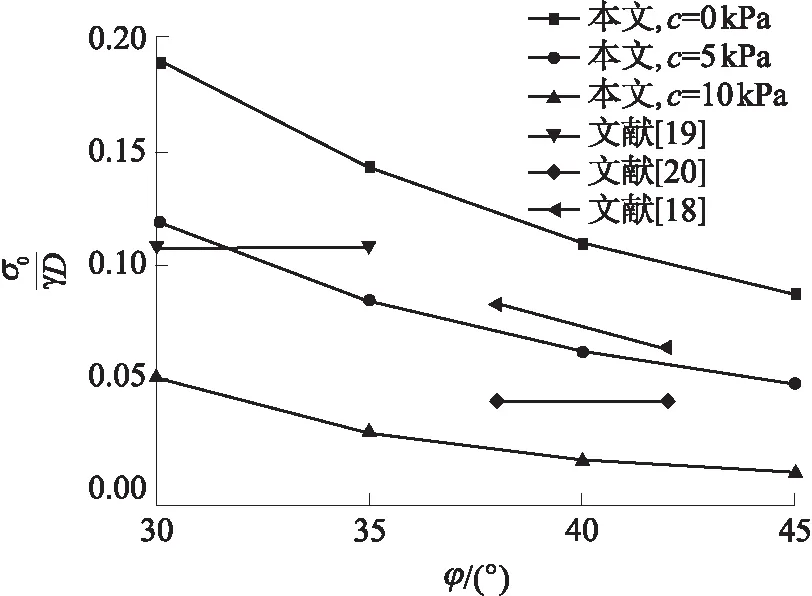
图6 归一化支护压力对比

2 讨论与运用

通过工程实践发现,在隧道的开挖过程中,循环进尺的选择对整个掌子面附近的稳定性有较大的影响,同时也是施工单位针对不同地质条件合理调整施工进度与造价的重要考量,而通过前述计算模型的推导得到的式(18)可为工程提供参考.在该极限平衡体系中,掌子面底部稳定与循环进尺段的平衡通过边界条件得到满足,在不同的围岩参数下,可优化得出最佳的循环进尺.

当内摩擦角φ=25°、H/D=1、γ=20 kN/m3时,在不同的黏聚力作用下,随着循环进尺的增大,掌子面所需的支护力同比增长,如图7所示.

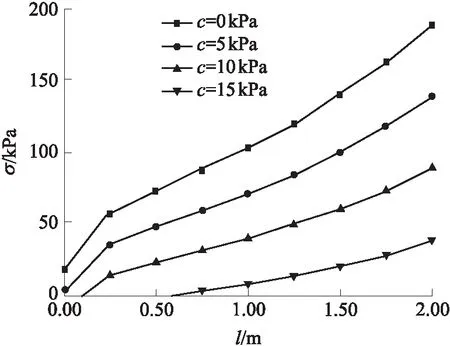
图7 支护力与循环进尺的关系

从图中可以看出:当循环进尺为0时,即使黏聚力较小,所需的支护力最大也不超过18 kPa;当循环进尺增大到0.25 m时,所需支护力急剧增长,且增长幅度随着围岩黏聚力的减小变得更大,这表明在考虑隧道掌子面施工稳定性时,虽然循环进尺是短期存在的,但对掌子面附近围岩状态的改变甚大,其影响在施工阶段应予以重视;当循环进尺在0.25～1.00 m时,随着循环进尺的增加,支护力的增长较为均匀,增长幅度比0.00～0.25 m段支护力的增长幅度要小,反映了掌子面在该围岩条件下开挖时,若循环进尺在0.25～1.00 m之间,则所需的支护力随着循环进尺的增加可近似等比例的增加,施工单位可综合实际情况选择恰当的循环进尺,更好地实现安全施工与便利;当循环进尺大于1.00 m时,支护力随着循环进尺的增加而增大,增长率也随循环进尺持续增大,并且黏聚力越小,这种现象越明显,这表明,当循环进尺过大时,掌子面与循环进尺区域的综合稳定性仅靠掌子面支护力去维持是难以为继的,表现出上部塌落体对掌子面的影响随着循环进尺的增大而逐渐减小,而循环进尺段自身的稳定开始占据主导,破坏形态可能发生了改变.

当黏聚力逐渐增大时,维持掌子面平衡所需的支护力会逐渐减小,如图8所示.一般而言,当循环进尺选定之后,掌子面支护力与黏聚力基本上呈线性关系,且黏聚力的增长极大地减小掌子面的支护力.这表明,在进行隧道施工方案对比时,选择黏聚力的改善比实施支护力提升的效果更好.从图8中可知,在2 m循环进尺范围内,黏聚力最大值不超过18.19 kPa,故在围岩中的黏聚力较大(超过18.19 kPa)时,可认为该围岩条件较好,循环进尺段对掌子面整体稳定性的影响较小,而在围岩条件较差的地质环境(黏聚力小于18.19 kPa)中,仅靠围岩自身条件不足以维持平衡,需综合考虑掌子面支护方式与拱顶加固方式来达到循环进尺的最优,顺利通过不利区域.

图8 支护压力与黏聚力的关系

从图8中亦可以看出,当黏聚力较小时,在不同的循环进尺区间,支护力的选择范围较大,其中0.00～0.50 m区间值最大,随后区间值随着循环进尺的增大而缓慢逐步增加,当达到循环进尺为2.00 m时,支护力达到189.3 kPa,所需支护力较大,钻爆法施工较难达到,因此,可通过图8各循环进尺区间综合支护力与黏聚力改善措施来达到施工预期.

当c=10 kPa,H/D=1,γ=20 kN/m3时,支护力与内摩擦角的关系如图9所示.从图9与式(2)可以看出:当内摩擦角增大时,拱顶螺旋半径减小,作用于掌子面的支护力逐渐减小,但当内摩擦角增大到45°时,不同循环进尺下的支护力都逐渐趋于接近,且数值较小;当内摩擦角增大时,拱顶受到两侧摩擦力的影响较大,拱顶逐渐趋于稳定,且作用于下部掌子面的应力随内摩擦角的增大而减小,则掌子面需提供的支护力也逐步减小,故在实际施工中,提升内摩擦角对改善掌子面稳定性的效果比较明显,但当内摩擦角大于30°时,改善内摩擦角对支护力的提升效果相对较差,说明掌子面发生整体滑动的可能性增大.

从图9中也可以发现,当内摩擦角较大时,不同循环进尺之间的支护力差别逐渐减小,故在施工条件允许的情况下,可适当提升支护强度,使得实际操作中可优先选择较大的循环进尺施工,提升效率.

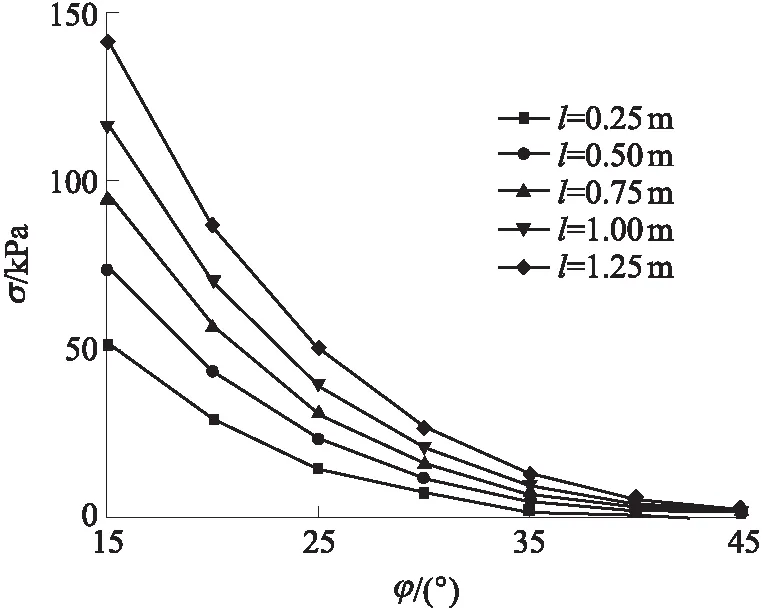
图9 支护压力与内摩擦角的关系

Fig.9 Support pressure as a function of the internal friction angle

在黏聚力为10 kPa时,内摩擦角与循环进尺的关系如图10所示.从图中可知:不同内摩擦角下,支护力与循环进尺同步增长,当循环进尺小于0.50 m时,内摩擦角越小,支护力的增长幅度越大,说明循环进尺对整个掌子面的区域稳定性的影响较大,与图7结论一致;当循环进尺大于0.50 m时,支护力的增长速率随着循环进尺的增长趋于均匀,但随着内摩擦角的增大,增长率趋于减小,实际上,在该围岩条件下,当内摩擦角增大到45°时,掌子面是接近稳定的.

图10 内摩擦角与循环进尺的关系

Fig.10 Internal friction angle as a function of the round length

在施工时,时常采用核心土施工方式,此时作用于掌子面的支护力较为稳定,通过前述分析可知,黏聚力对提升循环进尺的效果较明显,如图11所示.从图中可以看出:当循环进尺为0时,即使掌子面支护力为0,黏聚力达到6.47 kPa即可以维持平衡;当循环进尺逐渐增加时,所需黏聚力同步增大,在循环进尺0.00～0.25 m阶段的增长斜率明显大于0.25～1.75 m阶段,再次说明循环进尺对整体稳定性的影响较大,同时,一旦考虑循环进尺之后,黏聚力的提升需求相应减缓许多,说明当预留核心土确定之后,掌子面支护力也就确定,此时更需关注掌子面前方核心土的性能提升以有效地提升循环进尺.

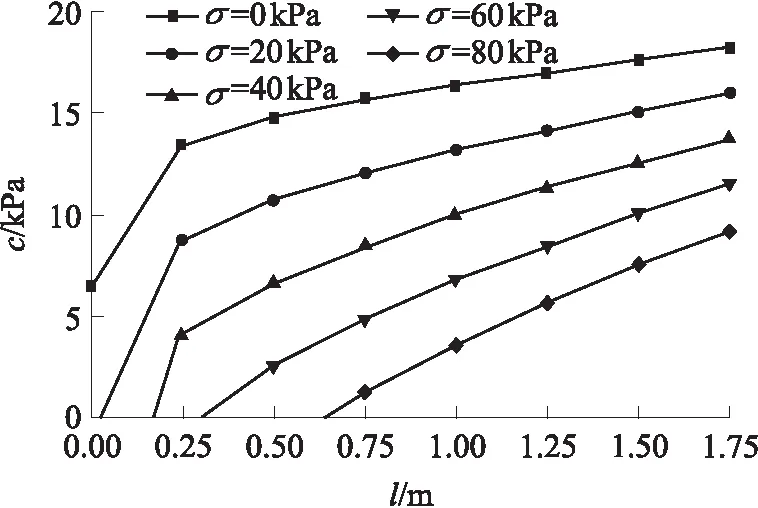
图11 黏聚力与循环进尺的关系

从图11中还可以看出,当支护力较大时,即使黏聚力较小,也能保证一定的循环进尺开挖,但这种支护力需求在实际的钻爆法施工中是较难达到的,结合图7可发现,在黏聚力较小的情形下(小于5 kPa),循环进尺最好控制在1 m以下.

3 工程对比与运用

3.1 工程对比

在北京长安街6条过街通道结构施工设计中[4- 5],根据北京市要求,只能采取暗挖且结构地板顶面距地面不允许超过4.7 m,结构净宽(单跨)10 m,净高不小于2.5 m,扣除结构厚度、装饰厚度、防火层厚度等,覆土只剩1.2 m(如图12所示),不允许交通中断,因而施工中确保地面安全是十分重要的.

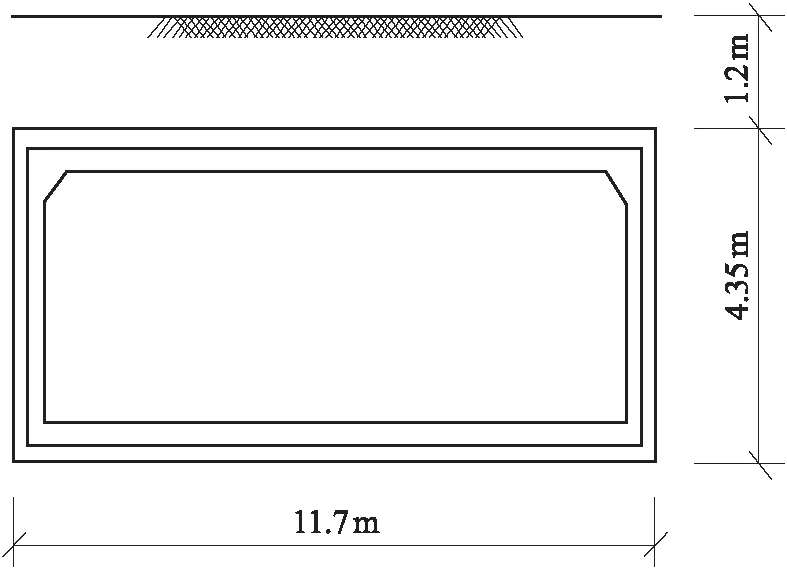
图12 地下通道示意图

从地表以下2～3 m分别为人工堆积层(c=8 kPa,γ=18.0 kN/m3,φk=30°)、亚黏土(c=15 kPa,γ=18.0 kN/m3,φk=35°)、第四纪沉积层轻中亚黏土(c=24 kPa,γ=18.5 kN/m3,φk=40°),结构顶部全部在人工堆积层中通过,侧墙底板在堆积层及亚黏土中通过.

在该围岩条件下,王志达等[4]根据太沙基理论得出循环进尺为0.82 m,惠丽萍等[5]计算得出循环进尺为0.77 m,塌落拱高为0.433 m,从纵向开挖看,因埋深较浅,如果循环进尺为0.77～0.82 m,则势必造成冒顶而使工程无法实施,深埋条件也难以达到要求,因此实际工程采用的开挖进尺为0.50 m.根据文中提供的破坏模式,参数按不利原则选取,即c= 8 kPa,γ=18.0 kN/m3,φk=30°,根据式(18)可得,在掌子面无支护力情况下,循环进尺为0.44 m,虽然比实际采用的循环进尺偏小,但对浅埋隧道而言更安全,若需提高施工效率,可改善围岩条件,如通过注浆、预留核心土等措施来提高黏聚力与支护力,有效提升循环进尺长度.

3.2 工程运用

工程中不仅关注循环进尺,亦关注开挖高度.在掌子面的支护力确定的情况下,通过开挖高度的调整可优化循环进尺,提升施工效率.循环进尺与开挖高度的关系如图13所示,循环进尺随着开挖高度与隧道高的比值的增大而减小,当支护力较大,且开挖高度与隧道高的比值在0.3～0.4之间时,其循环进尺的变化范围相对较小,在开挖高度接近隧道高度时,循环进尺的变化范围更小,且趋于0.这说明在实际施工中,存在一个开挖高度对循环进尺影响较大的区域,这个区域范围随着支护力的增大而增大,反映了众所周知的事实:支护力越完善,循环进尺选择的余地越大;当支护力较小时,低开挖高度是比较合适的选择,即采用台阶法或三台阶法等开挖方式.

图13 循环进尺与开挖高度比关系Fig.13 Relationship between round length and excavation height ratio

从图13中亦可以看出,随着支护力的增大,循环进尺与开挖高度比的曲线更趋平滑,说明掌子面支护力的增长,使得掌子面受力状态改善而减弱了循环进尺对掌子面的影响,但支护力对提升循环进尺的效果是随其增大而减弱的,尤其是在低开挖高度时,说明盲目地增大掌子面的支护力并不总是能最优化循环进尺,有临界性.

4 结论

文中围绕隧道循环进尺问题,考虑了掌子面循环进尺与超前核心土的稳定性,推导了相应的计算公式,分析了支护力、黏聚力、内摩擦角、开挖高度对循环进尺的影响,并与实际工程进行了对比,得到了一些有益的结论:①该模式计算结果与已有的试验和数值结果接近,证实了该模式具有一定的合理性;②循环进尺在实际施工中虽然是短期存在的,但其对掌子面附近围岩状态的改变甚大,使得掌子面支护力迅速增长,因此在施工阶段考虑隧道掌子面稳定性时需加入循环进尺的影响;③黏聚力与内摩擦角对改善循环进尺、掌子面区域稳定性具有重要的意义,而支护力对该区域的影响具有临界性,不可盲目增长.

[1] 王立川.浅埋偏压隧道围岩压力与开挖进尺优化的极限分析方法 [D].长沙:中南大学,2011.

[2] ANAGNOSTOU G,KOVARI K.Facestability conditions with earth-pressure-balanced shields [J].Tunnelling and Underground Space Technology,1996,11(2):165- 173.

[3] LEE Y Z,SCHUBERT W.Determination of the round length for tunnel excavation in weak rock [J].Tunnelling and Underground Space Technology,2008,23(3):221- 231.

[4] 王志达,龚晓南.浅埋暗挖人行地道开挖进尺的计算方法 [J].岩土力学,2010,31(8):2637- 2642. WANG Zhi-da,GONG Xiao-nan.Calculation method of digging length in underpass with underground excavation under shallow cover [J].Rock and Soil Mechanics,2010,31(8):2637- 2642.

[5] 惠丽萍,王良.浅埋暗挖土质隧道开挖进尺的理论探讨 [J].铁道标准设计,1995(11):25- 27. HUI Li-ping,WANG Liang.The theoretical analysis of round length in the shallow tunnel [J].Railway Standard Design,1995(11):25- 27.

[6] 李达,李永生,罗占夫.复杂条件下隧道开挖循环进尺优化方法研究 [J].岩土力学,2013,34(2):498- 502. LI Da,LI Yong-sheng,LUO Zhan-fu.Study of footage optimization method of tunneling cycle under complicated conditions [J].Rock and Soil Mechanics,2013,34(2):498- 502.

[7] 许金华,何川,周艺,等.基于台阶法的极破碎软岩隧道开挖进尺优化研究 [J].水文地质工程地质,2013,40(2):42- 48. XU Jin-hua,HE Chuan,ZHOU Yi,et al.Research on construction optimization and safety control technology for complicated condition’s tunnel [J].Hydrogeology & Engineering Geology,2013,40(2):42- 48.

[8] ANAGNOSTOU G.The contribution of horizontal arching to tunnel face stability [J].Geotechnik,2012,35(1):34- 44.

[9] LEE Y-Z,SCHUBERT W,KIM C-Y.The influence of the round length on the stability of tunnel face and unsuppor-ted span [M]∥Underground Space Use:Analysis of the Past and Lessons for the Futur.London:Taylor & Francis Group,2005:211- 223.

[10] 张佳华,杨小礼,张标,等.基于非线性破坏准则的浅埋偏压隧道稳定性分析 [J].华南理工大学学报(自然科学版),2014,42(8):97- 103. ZHANG Jia-hua,YANG Xiao-li,ZHANG Biao,et al.Stability analysis of shallow bias tunnels based on nonlinear failure criterion [J].Journal of South China University of Technology(Natural Science Edition),2014,42(8):97- 103.

[11] MOLLON G,DIAS D,SOUBRA A H.Rotational failure mechanisms for the face stability analysis of tunnels dri-ven by a pressurized shield [J].International Journal for Numerical and Analytical Methods in Geomechanics,2011,35(12):1363- 1388.

[12] YANG X L,ZHANG Dao-bin,WANG Zhuo-wei.Upper bound solutions for supporting pressures of shallow tunnels with nonlinear failure criterion [J].Journal of Central South University,2013,20(7):2034- 2040.

[13] YANG X L,HUANG F.Three-dimensional failure mecha-nism of a rectangular cavity in a Hoek-Brown rock medium [J].International Journal of Rock Mechanics and Mining Sciences,2013,61:189- 195.

[14] FRALDI M,GUARRACINO F.Evaluation of impending collapse in circular tunnels by analytical and numerical approaches [J].Tunnelling & Underground Space Technology,2011,26(4):507- 516.

[15] FRALDI M,GUARRACINO F.Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections [J].International Journal of Solids and Structures,2010,47(2):216- 223.

[16] SUBRIN D,WON H.Tunnel face stability in frictional material:a new 3D failure mechanism [J].Computes Rendus Mecanique,2002,330(7):513- 519.

[17] ANAGNOSTOU G,PERAZZELLI P.The stability of a tunnel face with a free span and a non-uniform support [J].Geotechnik,2013,36(1):40- 50.

[18] MOLLON G,DIAS D,SOUBRA A H.Face stability ana-lysis of circular tunnels driven by a pressurized shield [J].Journal of Geotechnical and Geoenvironmental Engineering,2009,136(1):215- 229.

[19] KIRSCH A.Experimental investigation of the face stabi-lity of shallow tunnels in sand [J].Acta Geotechnica,2010,5(1):43- 62.

[20] CHAMBON P,CORT J F.Shallow tunnels in cohesionless soil:stability of tunnel face [J].Journal of Geotechnical Engineering,1994,120(7):1148- 1165.

Limit Equilibrium Analysis of Round Length in Tunnel Excavation

LIANGQiao1,2YANGXiao-li1CHENXiang3

(1. School of Civil Engineering, Central South University, Changsha 410075, Hunan, China; 2.College of Construction Engineering, Hunan Institute of Engineering, Xiangtan 411104, Hunan, China; 3. Hunan Xiangping Road and Bridge Construction Co., Ltd., Changsha 410075, Hunan, China)

In order to determine the round length reasonably in the process of tunnel excavation, the logarithmic spiral failure mode of advanced core soil on the tunnel face is proposed, which consists of two parts respectively considering vaults and advanced core soil in the surrounding rock. Then, in light of Janssen’s silo theory and Mohr-Coulomb strength criterion, a calculation formula of vertical force loading on vaults is established, and the formula to calculate the round length in advanced core soil on the tunnel face, which is governed by such relevant parameters as internal friction angle, cohesive force, support pressure and excavation height, is set up on the basis of logarithmic spiral failure mode. The results show that (1) the round length produces very important impact on the stability of tunnel face, especially in the construction stage; (2) the support pressure on tunnel face considering round length may increase rapidly; and (3)the reinforcement of cohesive force and internal friction angle is of great significance for the improvement of round length and tunnel face stability, while the support pressure is of a critical value in terms of affecting tunnel face.

round length;limit equilibrium;logarithmic spiral;failure modes;advanced core soil

2016- 04- 01

国家“973”计划项目(2013CB036004);国家自然科学基金资助项目(51178468,41302226);湖南省自然科学基金资助项目(2015JJ4019) Foundation items: Supported by the National Program on Key Basic Research Project of China(2013CB036004),the National Na-tural Science Foundation of China(51178468,41302226) and the Natural Science Foundation of Hunan Province(2015JJ4019)

梁桥(1981-),男,博士生,讲师,主要从事岩土工程研究.E-mail:liangqiao81@163.com

1000- 565X(2017)05- 0113- 07

U 451+.2

10.3969/j.issn.1000- 565X.2017.05.016