“从问题到方程”教学设计

文| 刘 畅

一、教学背景

《义务教育课程方案（2022 年版）》在课程实施意见中提出：培养学生会用数学的眼光观察世界、会用数学的思维思考世界、会用数学的语言表达世界。基于此，笔者以“从问题到方程”为例，贯彻落实新课标的要求。“从问题到方程”这一课题中的“到”韵味深长，笔者认为，更多的要带领学生经历探索实际问题中数量关系的过程，教给学生探究问题的方式，并注重对学生抽象能力、应用意识和建模能力的培养。

二、教材分析

“从问题到方程”是苏科版数学七年级上册第四章第一节的内容，是在学习了有理数以及代数式之后探究的又一个重要内容。这节课重在探索实际问题中的数量关系，并用方程描述，再归纳总结出一元一次方程的概念，并使学生意识到方程是刻画现实世界的数学模型，为后面解一元一次方程以及用一元一次方程解决实际问题做铺垫，并且为后续二元一次方程、一元二次方程的学习提供了思路。

三、学情分析

学生在小学时期就学习过方程的概念，但他们对从生活问题中抽象出数学模型乃至方程较为陌生。到了初中阶段，我们进一步加强对方程的学习，经历了从生活中的实际问题到建立方程的过程，使学生充分感受到方程的简明性和优越性。

四、教学目标

1.探索实际问题中的数量关系，并用方程描述，通过对多种实际问题中数量关系的分析，使学生初步感受方程是刻画现实世界的有效模型。

2.通过观察，归纳一元一次方程的概念。

3.培养学生的数学建模能力，提高抽象问题的解决能力。

五、教学重难点

探索实际问题中的等量关系以及归纳一元一次方程的概念。

六、教学过程

（一）创设情境，导入新课

（出示购买物品称重的图片）

师：在日常生活中，我们利用天平性质来测量物体质量，那么，天平的原理是什么呢？

生：等量！

师：你能说一说其中的等量关系式吗？

生：两边重量相同。

出示一个1 g 小球、2 个同样的大球与5 g 砝码在天平上（如图1）。

图1

师：如何精准地知道双方的等量关系呢？你们有什么方法？

生：天平两边物体重量相等，可以用等式方法。

出示笛卡尔对数学问题的理解。

师：著名的数学家、哲学家以及几何的创始人笛卡尔认为世间万物中的一些问题都可以转化为数学问题，再将这些数学问题进一步转化为代数问题，最后将代数问题再简化成解方程。从他的话语中我们可以看出什么？

生：我们可以知道世界万物都能转化为数学问题，而这些数学问题我们都可以运用解方程的方法来解决。

师：找到等量关系就可以根据等量关系式列出方程吗？这个方程又是一个什么方程呢？我们又该如何解这个方程呢？

生：2 个相同大球的质量加1 个1 g 小球的质量等于5 g 砝码的质量。

师：方程可以看作是数学中描述相等关系的一架天平。今天我们共同学习“从问题到方程”。

（设计意图：本环节借助实例的方式，引导学生再次复习等式的性质，同时，通过复习的方式，引出本次探究的问题，再从“天平”这一实际问题入手，引导学生说出其中的等量关系，并尝试建立方程，从而引出本课的课题。）

（二）探究新知

1.探索发现，了解天平与等式关系

出示2x+1=5

师：根据刚刚我们找出的等量关系，发现通过方程描述这类等量关系最为简明，因此，请大家根据等式的性质尝试列出方程。

生：设一个大球的质量为xg，就可以得到：2x+1=5。

2.由天平看等式性质

师：你知道天平的特性是什么吗？如何才能保持天平两边的平衡呢？

生：两边质量相同。

师：没错，天平的原理就是两边质量相同，这样才能保持平衡。那么，你还能运用天平原理，也就是方程来描述等量关系吗？

问题一：

师：学校开展篮球联赛，规定：胜一场得2 分，负一场得1 分。某篮球队比赛了12 场，共得20 分。那么，你该如何去描述其中数量之间的等量关系？

生：胜场得分+负场得分=20 分。

师：如何建立方程呢？

生：设胜了x 场，可知负了（12-x）场。得到方程：2x+1（12-x）=20。

问题二：

师：想一想：以绳三折测之，绳多四尺；若将绳四折测之，绳多一尺。绳长、井深各几何？这个问题究竟问的是什么，从中你发现哪些信息呢？

师：同学们可以通过画示意图理解这个问题的意思。

（展示学生画的图，如图2 所示）

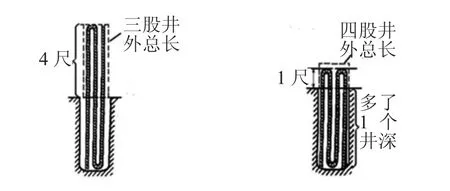
图2

生：用绳子量井深，把绳三折来量，井外余绳四尺；把绳四折来量，井外余绳一尺。绳长、井深各几尺？

师：你能描述其中的等量关系吗？

生：3×（井深+4）=4（井深+1）。

师：等号两边都表示的是什么量？

生：绳长。

师：如果设井深为x 尺，如何列出方程？

生：设井深为x 尺。可列出方程：3（x+4）=4（x+1）

师：还有其他的等量关系吗？还可以设绳长为x尺来列方程组。

列式略。

师：实际问题中已知量和未知量之间的相等关系，可以用多种不同的方式描述。通过比较可以看出，用方程描述这种等量关系最简明。

（设计意图：旨在培养学生的思维，同一个问题，从不同的等量关系、不同的角度都能解决这个问题。）

3.数学运用

用方程描述下列问题中数量之间的等量关系：

某公园的门票价格为：成人票8 元/张，儿童票3元/张。买门票共花了44 元，共有8 人去公园。

师：你能找出其中的相等关系吗？

生：成人票的总价+儿童票的总价=44 元。

设成人x 人，可知儿童为（8-x）人，可列方程：8x+3（8-x）=44。

变式：某公园的门票价格为：成人票8 元/张，儿童票3 元/张。买门票共花了44 元。你能找出其中的相等关系并列出方程吗？

生：成人票的总价+儿童票的总价=44 元。

设成人x 人，儿童y 人，可列方程：8x+3y=44。

师：这两个问题之间有什么联系与区别？

生：联系是等量关系是一样的，区别是第二个问题有两个未知量，因此要设两个未知数，而第一个问题只有一个未知量，因此只要设一个未知数。

师：总结得很到位！

（设计意图：在这个情境中，等量关系不变，但未知数的设法不一样了，让学生能够概括其中的联系与区别，为后面一元一次方程概念的归纳与辨析做铺垫。）

甲、乙两人加工同一种服装，乙每天比甲多加工1 件，乙加工服装24 件所用时间与甲加工服装20 件所用时间相同。

师：如何用方程来描述其中数量之间的相等关系？

生：乙加工服装24 件所用时间=甲加工服装20件所用时间。

设甲每天加工x 件，可知乙每天加工（x+1）件。则可列出方程：

正方形桌面的面积是2 m2，求它的边长。

生：设正方形的边长为x m，可列方程：x2=2。

4.自主归纳，形成方法

师：在刚刚我们描述的过程中，你们的思路是什么样的？

生：审题、寻找等量关系、设未知数、列方程。

（设计意图：让学生经历“从问题到方程”的过程，引导学生自主归纳其一般步骤，从而培养学生的归纳概括能力，以形成自己的知识体系，为后续用方程解决实际问题做铺垫。）

（三）归纳一元一次方程的概念

出示：①2x+1=5；②2x+1（12-x）=20；③3（x+4）=4（x+1）；④8x+3（8-x）=44；⑤8x+3y=44；⑥

师：观察上述问题中的方程，你能将它们分类吗？

（学生小组讨论交流）

生：⑤中含有两个未知数，其他的方程都只含有一个未知数。

生：⑥方程等号两边不是整式，其他方程的两边都是整式。

生：⑦中未知数的次数是2 次，①②③④⑥中未知数的次数都是1 次。

师：同学们归纳得真全面！我们把像①②③④这样只含有一个未知数并且未知数的次数是一次的方程叫做一元一次方程。你能再写几个一元一次方程吗？

（展示学生的作品，让其他同学进行辨析）

（四）练习巩固

1．下列式子中：①5x+3y=0；②6x2-5x；③3x＜5；④x2+1=3；⑤x+1=3 是一元一次方程的有（）。

（设计意图：本题考查了一元一次方程的概念，通过观察、辨析，有助于学生深刻地理解一元一次方程的概念。）

2．用方程描述下列问题中数量之间的等量关系：

（1）一头半岁的蓝鲸体重22 t，90 天后体重为30.1t。设蓝鲸体重平均每天增加xt，可得方程______。

（2）把50 kg 大米分装在3 个同样大小的袋子里，装满后还剩余5 kg，设每个袋子可装大米xkg，可得方程______。

（3）甲、乙两城市间的铁路经过技术改造后，列车在两城市间的运行速度从100 km/h 提高到120km/h，运行时间缩短了2 h。设甲、乙两城市间的路程为xkm，如何列方程？

（设计意图：本题让学生再次经历用一元一次方程解决实际问题的过程，巩固用一元一次方程解决实际问题的一般步骤。）

3.请你赋予2x+1=5 其他的实际意义。

（设计意图：让学生编题目，是为了让学生更深刻地理解知识并应用知识，培养学生的发散性思维，让学生在交流、讨论中碰撞出思维的火花。）

七、案例小结

本节课的设计重点没有放到一元一次方程的概念，而是着重带领学生经历“从问题到方程”的过程。如何分析问题中的数量关系，如何找到等量关系，如何列出方程，是本节课的核心内容。通过这一系列的教学步骤，学生不仅能够学到一元一次方程的基本知识，还能够在解决实际问题的过程中培养数学建模和解决问题的能力。这种实践性的教学方法有助于学生更好地理解和应用数学知识。