基于常项值和先验节点的全纯嵌入潮流计算方法
2023-02-27姚超凡李华鹏陈厚合
李 雪,姚超凡,姜 涛,李华鹏,陈厚合
(1.东北电力大学 现代电力系统仿真控制与绿色电能新技术教育部重点实验室,吉林 吉林 132012;2.东北电力大学 理学院,吉林 吉林 132012)
0 引言
潮流计算是电力系统安全稳定分析的基础,基于牛顿-拉夫逊(Newton-Raphson,NR)法的潮流计算方法已在电力系统中得到广泛应用[1]。但NR法的局部收敛特性使得该方法对初值的选择较为敏感,实际计算时,不合理的初值将导致潮流计算不收敛,且当潮流不收敛时,无法明确判定是由NR法缺陷导致的还是由系统在该运行方式下不存在潮流解导致的[2]。随着电网互联规模的不断扩大,新能源和电力电子设备占比不断提高,电力系统运行方式呈现出明显的多样化、复杂化等特征[3-4],这使得电力系统潮流求解更为复杂。因此,研究收敛性和鲁棒性更强的潮流计算方法,探索适用于新型电力系统的潮流求解新理论,对电力系统的规划和运行具有重要意义[5]。
针对NR法在电力系统潮流求解中存在的问题,西班牙学者Antonio Trias于2012年首次提出将全纯嵌入法(holomorphic embedding method,HEM)应用于求解电力系统非线性潮流方程的初步构想,为电力系统潮流计算提供了新思路[6]。HEM基于复分析理论,将潮流待求量嵌入复参数后构建全纯函数,通过显式化隐式全纯函数实现潮流的求解,该方法无需提供初值且无需形成Jacobi矩阵,具有良好的收敛性。理论上:若系统存在潮流解,则HEM可保证收敛至高电压解;若系统不存在潮流解,则会出现解析延拓大幅振荡的现象,这为调度人员提供了明确的参考[7]。基于HEM的这一优点:文献[8-9]将HEM应用到电力系统交直流潮流计算中;文献[10]采用HEM求解电力系统的概率潮流;文献[11]采用HEM计算电力系统的负荷裕度;文献[12]基于HEM提出一种预测系统电压薄弱节点的方法;文献[13]提出通过嵌入多个复参数来构建多维嵌入全纯函数,以搜索电力系统的静态电压稳定域边界;文献[14]计及异步电机负载特性,采用HEM分析电力系统的动态电压稳定性。
虽然HEM已在电力系统潮流计算和安全稳定分析中得到了应用,但采用HEM求解大规模电力系统潮流时,计算效率仍存在不足。文献[15]提出将HEM与高斯-赛德尔法和快速解耦法结合,提高HEM在大规模电力系统潮流求解中的计算效率,但所提方法需与传统潮流算法相结合才可体现出较好的计算性能,且每次更新潮流待求量全纯函数的幂级数高阶项系数后,需计算所有节点的电压逼近值,计算冗余度高是制约该方法求解效率的主要原因。文献[16]指出在利用HEM求解大规模系统潮流时,用于全纯函数显式化的幂级数阶数过高是导致实际系统潮流计算效率较低的另一主要原因,且由于计算机双精度的限制,潮流解的精度难以得到保证。文献[17]分析当幂级数阶数过高时,求解过程中的截断误差对HEM求解电力系统潮流的影响。文献[18]通过从数学的角度分析HEM中所采用的基于Padé近似的解析延拓方法发现,在不考虑计算机截断误差的情况下,当幂级数计算阶数过高时,Padé近似存在伪零极点对(Froissart doublets现象),将影响潮流收敛。
针对上述采用HEM求解潮流时存在的问题,本文提出一种基于常项值和先验节点(priori buses)的全纯嵌入潮流计算方法(holomorphic embedding load flow method,HELM)。首先,构建基于常项值的全纯嵌入潮流模型,通过动态更新常项值避免高阶Padé近似计算,提高HEM的收敛性;其次,定义系统先验节点,提出先验节点电压幅值预判机制以减少计算冗余,提高求解效率;然后,提出2种基于全纯嵌入潮流的发电机节点类型转换策略;最后,通过4~25 000节点不同规模的交流测试系统对所提方法的准确性和有效性进行分析、验证。
1 HELM基本理论
采用全纯嵌入理论求解电力系统潮流的实质是将电力系统的潮流求解问题转化为全纯函数显式化问题,本节简要介绍电力系统HELM的基本求解流程。
设电力系统中节点数为N,潮流待求变量集合为z,电力系统潮流方程f(z)=0可表示为:

将潮流待求量嵌入复参数α后,根据不同类型节点特点所建立的HELM计算模型f(z(α))=0参考文献[9]。其中任意全纯函数p(α)在其定义域内各点的邻域均无限可微,在p(α)定义域内任一值α0处可将该函数展开为式(2)所示的泰勒级数[6]。
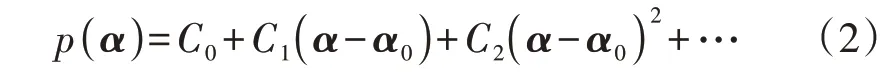
式中:Cn(n=0,1,2,…)为泰勒级数中n次幂的幂级数系数。
将HELM计算模型中的全纯函数以类似式(2)的展开式替代后,所得关于复参数α的多项式关系参考文献[9]。进一步根据多项式等式两边同阶项幂级数系数相等的原则,可推导出各全纯函数泰勒级数展开式中高阶项系数的递归关系。同时,当令复参数α=0时,可得各泰勒级数常数项值,如式(3)所示。根据常数项值和递归关系,可逐阶求取高阶项幂级数系数,实现全纯函数显式化。所有全纯函数显式化过程如附录A图A1所示。

式中:Wi[0]、Vi[0]分别为全纯函数Wi(α)、Vi(α)泰勒级数展开式中的常数项,为复数,Wi(α)=1/Vi()α。
全纯函数显式化后,由于嵌入复参数α=1时,全纯嵌入潮流方程与原潮流方程组完全等价,因此系统节点电压集V(1)即为所求实际电压解。基于解析延拓理论求解所有节点电压函数V(α)在α=1处的逼近值时,Padé近似不仅可扩大级数V(α)的解析范围,而且具有较高的精确度[16]。传统HELM采用矩阵法计算Padé近似,存在较多复杂的矩阵运算,求解效率较低,为此,本文借鉴文献[8]中的Bauer’s Eta法,求解时仅需将Bauer’s Eta表中第1行元素相加即可得到泰勒级数逼近值,可有效提高HELM电压逼近值的求解效率。
2 基于常项值和先验节点的HELM潮流求解方法
对于拓扑结构较复杂的大规模电力系统,传统HELM存在求解效率、收敛性等方面的不足。本节提出一种基于常项值的全纯嵌入潮流计算方法(HELM based on constant values,CHELM),以实现潮流的准确求解;在此基础上提出先验节点电压幅值预判策略,以减少HELM中的冗余计算量(将基于常项值和先验节点的HELM记为P-CHELM),提高大规模电力系统全纯嵌入潮流的求解效率;进一步考虑潮流计算中PV节点无功越限问题,提出适用于CHELM和P-CHELM的PV-PQ节点类型转换策略,以实现大规模电力系统全纯嵌入潮流的准确、高效求解。
2.1 基于CHELM的电力系统潮流求解方法2.1.1 全纯嵌入潮流模型的构建
本节所提基于常项值的全纯嵌入潮流模型为:

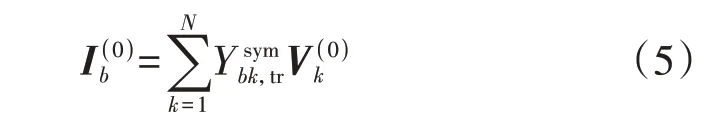
HELM模型需满足3个构建条件[17]:
1)当嵌入复参数α=0时,全纯嵌入潮流方程组f(z(0))=0应易于求解,以便得到幂级数常数项;
2)当α=1时,f(z(1))=0应与原潮流方程组完全等价,从而保证z(1)为实际潮流解;
3)由方程组f(z(α))=0所确定的隐式函数z(α)具有全纯特性。
基于上述条件,对所提模型的合理性进行分析、验证。首先,当嵌入复参数α=0时,CHELM计算模型可化简为(PV节点l的无功全纯函数Ql(α)泰勒展开式中常数项Ql[0]=0):

由式(6)可知,当Ql[0]=0时,除平衡节点电压级数常数项Vr[0]=1外,对于PQ节点,有Vi[0]=V,对于PV节点,有Vl[0]=Vl(0),即CHELM中所引入的电压常项值即为电压全纯函数泰勒展开式中的常数项。然后,可由式(5)进一步计算出PQ、PV节点的电流常项值I、I。不同于传统HELM泰勒展开式中常数项取值固定的局限性,CHELM中的常数项取值极具灵活性,取任意值均可满足各等式条件要求。该特点与文献[15]中快速、灵活的HELM类似,可以选取不同的幂级数常数项作为计算起点,因此,可与高斯-赛德尔法、NR法等传统迭代法结合求解,提高全纯嵌入潮流的灵活性。虽然理论上常项值可任意选取,但在本文中,为保证所有系统潮流求解的通用性,仍选取式(3)所示各幂级数常数项进行计算。因此,本文所提全纯嵌入潮流模型满足HELM模型的构建条件1)。
当嵌入复参数α=1时,CHELM计算模型完全等价于式(1)所示潮流模型,满足HELM模型的构建条件2)。此外,文献[7]已在数学上证明在全纯嵌入潮流模型中引入多项式,如在PQ节点模型中引入复参数α的多项式(1-α)I,并不影响求解问题的全纯特性,因此,CHELM计算模型满足HELM模型的构建条件3)。
综上,本文所提CHELM模型完全满足HELM模型的3个构建条件。
2.1.2 全纯函数显式化
在求得幂级数的常数项后,需推导出幂级数高阶项系数与低阶项系数间的递归关系式,由此完成全纯函数显式化。首先将式(2)所示泰勒展开式代入CHELM计算模型式(4)中,根据多项式等式两边同阶项幂级数系数相等的原则,通过等式左右两边一阶项系数可得到递归关系式,如附录A式(A1)所示。当阶数n>1时,比较等式两边同次幂αn的系数,得到递归关系式,如附录A式(A2)所示。
由式(A2)可以看出:由PV节点电压幅值约束所推导出的递归关系式中,包含电压实部Vlre和虚部Vlim。为便于统一求解,所有节点电压待求量V均以实部、虚部表示为V=Vre+jVim,同时将导纳矩阵Y以电导G、电纳B表示(Y=G+jB),并代入式(A1)和式(A2)。令复数型递归关系等式两边实部、虚部分别相等,从而将整体求解过程转换为求解实数方程。
为便于采用计算机进行求解,本节以4节点系统为例推导高阶项幂级数系数的矩阵求解形式。其中,节点1为平衡节点,节点3为PQ节点,节点2和节点4为PV节点。所推导的CHELM高阶项幂级数系数求解的矩阵形式如附录A式(A3)所示。
2.1.3 常项值动态更新
虽然理论上CHELM计算模型中所引入的常项值可任意选取,但为保证求解的通用性,本文仍选取式(3)所示各幂级数零阶项系数作为计算起始点,进而根据式(A1)和式(A2)计算幂级数高阶项系数。然而,该计算与传统HELM类似,仍无法避免高阶幂级数计算及其所带来的Padé近似收敛性问题。根据上述常项值选取特性,本节进一步提出常项值动态更新策略,以提高Padé近似收敛性,进而增强潮流计算的收敛性和求解灵活性。采用CHELM计算电力系统潮流时,首先需设置幂级数计算阶数的上限nmax以及常项值更新的次数上限Rmax,根据式(3)所示常项值以及式(A1)和式(A2)所示幂级数高阶项系数递归关系,计算幂级数高阶项系数,以实现隐式全纯函数显式化。当幂级数阶数n达到阶数上限nmax时,以当前解析延拓所求的各节点电压逼近值Vb-pade更新各节点的电压常项值V,并由式(5)计算对应节点电流常项值I,然后更新递归关系式中的常项值,求解高阶项幂级数系数,直至最大功率不平衡量满足预设潮流精度要求,得到系统潮流解。当常项值更新次数R达到上限Rmax时,结束计算,以避免潮流计算陷入死循环。基于该策略的CHELM各全纯函数显式化过程如附录A图A2所示,图中Vi-pade、Vl-pade分 别 为PQ节 点i、PV节 点l的 电 压 逼近值。
2.2 先验节点选取策略
采用HELM求解电力系统潮流时,需要计算一定阶数的幂级数系数,所得电压逼近值才可满足计算精度要求。传统HELM在每次更新幂级数高阶项系数后,均采用解析延拓计算系统中所有节点的电压逼近值,若系统规模较大,则会产生较多冗余的计算量,导致求解效率较低。本节借鉴电力系统电压中枢点的概念和作用[19],提出先验节点计算策略如下:基于系统拓扑结构,统计所有PV节点的连接度(本文将节点所连支路数定义为连接度),将大于给定连接度阈值的所有PV节点作为先验节点;在幂级数高阶项系数更新后,由解析延拓Padé近似计算出所有先验节点的电压幅值Vpriori,并与给定电压幅值进行比较;当误差满足预设内循环精度ρin要求时,计算所有节点的电压逼近值,并分别由式(7)和式(8)得到功率Scalc及最大功率不平衡量mmax;将mmax与给定潮流外循环精度ε进行比较,直至满足精度要求,算法收敛,得到系统潮流解。
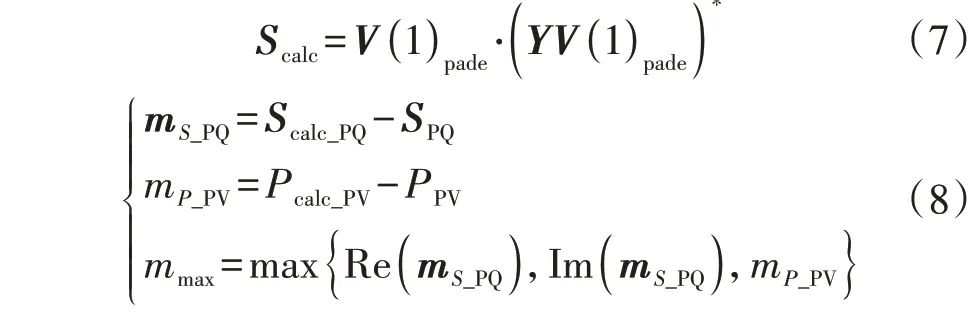
式中:V(1)pade为所有节点电压逼近值组成的列向量,其中1为复参数α的取值;“·”表示矩阵点乘运算;mS_PQ为PQ节点复功率不平衡量;mP_PV为PV节点有功功率不平衡量;Scalc_PQ、Pcalc_PV分别为计算所得PQ节点复功率、PV节点有功功率;SPQ、PPV分别为PQ节点给定复功率、PV节点给定有功功率;Re(·)、Im(·)分别表示取实部、虚部。
实际计算时,先验节点需根据系统拓扑结构选取合适的连接度阈值来确定,将所有大于连接度阈值的PV节点定义为先验节点,并进行潮流计算。附录A表A1给出了部分测试系统PV节点的连接度。
图1为采用本文所提方法得到的表A1各测试系统在不同连接度阈值下的潮流计算耗时。由图可知:当先验节点的连接度阈值为4时,测试系统的计算耗时最短(个别系统最佳阈值取值存在较小差异,但计算耗时相差仅为ms级),因此,本文在后续计算中将连接度大于4的PV节点作为先验节点,以提高CHELM的计算效率。

图1 不同连接度阈值下不同测试系统潮流计算耗时Fig.1 Load flow computational time of different test systems under different connectivity thresholds
2.3 节点类型转换
电力系统实际运行时,作为PV节点的发电机无功有可能越限,此时该节点将由PV节点转换为PQ节点,节点电压变为待求量。本节借鉴MATPOWER软件[20]中NR法的 节 点 类型转换方法,提出2种CHELM和P-CHELM节点类型间的转换方案。
1)方案1:在潮流初步收敛后,根据此时各节点的电压值,由式(9)计算出所有PV节点的无功出力,并与各发电机无功出力上下限进行对比,将所有无功出力越限节点全部转换为PQ节点,然后,继续采用式(3)所示常项值以及式(A1)和式(A2)的递归关系,根据CHELM计算系统新状态下的潮流解,不断重复上述过程,直至不存在越限节点为止。

式中:Qge_PV为PV节点注入无功功率;VPV为PV节点电压逼近值;YPV为节点导纳矩阵中的PV节点对应部分;Qload_PV为PV节点所带无功负荷。
2)方案2:在计算出初步潮流分布后,判断无功出力越限量最大的节点,仅将该节点转换为PQ节点,并采用CHELM不断计算潮流,直至满足所有节点的无功出力上下限约束,得到最终潮流解。
上述2种节点转换方案均可在所提CHELM及P-CHELM中实现,具体采用哪种转换方案,需结合电网中发电机的实际运行情况进行选择。方案1需将所有越限节点均转换为PQ节点,可以有效保证所有发电机的安全稳定运行,但越限节点较多时不符合运行准则,且存在部分PV节点被强制转换的可能性;而方案2在每次潮流收敛后仅将越限值最大的节点转换为PQ节点,可尽可能少地将越限节点转换为PQ节点,但是在潮流计算过程中,会存在部分发电机处于无功越限的状态下运行,影响电网的运行安全稳定性。因此,在实际工程中,应权衡利弊选择合适的转换方案。
2.4 计算流程
综上,本文所提基于CHELM和P-CHELM的电力系统全纯嵌入潮流求解算法计算流程如附录A图A3所示,具体步骤如下。
1)根据式(3)的初始常项值及式(A1)和式(A2)的递归关系求解幂级数高阶项系数,再利用Bauer’s Eta法求取先验节点电压逼近值。
2)若先验节点电压逼近值满足内循环精度要求,则进一步计算所有节点电压逼近值,并由式(7)计算此时节点注入复功率,由式(8)计算功率不平衡量,若功率不平衡量满足潮流精度,则执行步骤4);否则继续计算更高阶幂级数系数。
3)当幂级数阶数达到阶数上限nmax后,计算所有节点电压逼近值,并据此更新电压常项值,继而由式(5)更新电流常项值,继续计算高阶项系数以及先验节点电压值,转至步骤2)。
4)由式(9)计算PV节点无功出力,并与其限值进行对比:若存在越限情况,则选择节点转换方案进行节点类型的转换,再执行步骤1);否则,结束算法,输出潮流结果。
3 算例分析
为验证本文所提CHELM和P-CHELM在电力系统潮流计算中的准确性和有效性,本节通过节点数为4~25 000之间不同规模的测试系统进行分析、验证。
3.1 准确性与通用性验证
3.1.1 潮流结果验证
为验证所提方法的准确性和通用性,本节首先将所提CHELM、P-CHELM与传统HELM、NR法对不同规模测试系统的潮流计算结果进行对比。若NR法平启动的潮流计算不收敛,则采用MATPOWER软件所提供的初值进行计算。本文算例的计算精度均为10-3,幂级数阶数上限nmax=12,Padé近似计算均采用Bauer’s Eta法。对于300节点及以下规模系统,采用CHELM进行计算,对于1 000节点以上大规模测试系统,采用P-CHELM进行计算。将连接度大于4的所有PV节点作为先验节点,电压幅值预判精度设为10-7。附录B表B1以NR法潮流计算结果为基准,给出了传统HELM和所提CHELM潮流计算结果中电压幅值及相角的最大误差。
由表B1可以看出:对于各类测试系统,本文所提方法与NR法计算结果均一致,验证了本文所提方法的计算准确性。需要指出的是:P-CHELM是在CHELM的基础上引入了先验节点的计算思路,仅会提高计算效率,而不会影响潮流计算精度,因此,表B1中P-CHELM与CHELM的计算精度相同。可知,所提方法较传统HELM具有更好的潮流收敛性能。
表B1中,对于部分系统,传统HELM与CHELM的计算结果相同,这是由于这些系统采用CHELM进行计算时,不需要更新常项值即可收敛。由传统HELM与CHELM的递归关系以及图A1和图A2的显式化过程可知,若初次计算未达到阶数上限便可实现潮流收敛,则此时由于2种方法采用相同的幂级数常数项,且递归关系相同,因此2种方法的计算过程与计算结果均一致。分析发现,在145节点以下规模的系统中,常项值均不需要更新即可实现潮流收敛,此时2种方法的性能相同,并不能体现出本文所提CHELM的优势。而对于1 000节点以上的大规模测试系统,大多需更新常项值才能实现潮流收敛。由于常项值更新后2种方法的幂级数常数项及递归关系式均不同,求解的初始点以及求解过程将不同。采用传统HELM时会出现计算阶数过高,进而影响解析延拓和潮流收敛性;而CHELM由于设置了幂级数阶数上限、动态更新常项值等策略,可有效提高大规模电力系统全纯嵌入潮流的收敛性。
进一步将传统HELM的计算精度由10-3降至10-2,由于受传统HELM解析延拓收敛性较差的制约,表B1中Case 6 468rte等测试系统仍无法收敛,同时Case 2 848rte、Case 2 868rte系统的最高计算精度仅能达到10-2。表1给出了采用传统HELM与所提CHELM求解部分测试系统潮流时所能达到的最高计算精度。其中,传统HELM的幂级数阶数上限设为400,CHELM常项值最大更新次数设为30。由表可知,本文所提CHELM的计算精度远高于传统HELM。

表1 CHELM与HELM最高计算精度对比Table 1 Highest accuracy comparison between CHELM and HELM
3.1.2 节点类型转换方案验证
本节对所提CHELM节点转换方案进行验证。首先以Case 39节点测试系统为例,其中发电机G8的无功出力范围为0~250 Mvar,基态潮流下,该发电机无功出力为-1.37 Mvar,低于其无功出力下限,需将该发电机节点转换为PQ节点,以无功下限值作为G8的无功给定值(仅1个节点越限,方案1和方案2结果相同)。在更新节点类型后,继续采用所提CHELM计算得到最终收敛的潮流结果。表2给出了该场景下CHELM和NR法计算的各发电机节点的电压幅值和相角(表中2种方法的电压幅值均为标幺值)。由表可知:该场景下,CHELM和NR法计算出的各发电机节点电压幅值和相角一致,电压幅值和相角的相对误差均为0。在潮流计算结果中,CHELM相对于NR法的电压幅值最大绝对误差为2.16×10-6p.u.,电压相角最大绝对误差为1.23×10-4°,2种方法均将G8所在节点由PV节点转换为PQ节点。该结果验证了所提CHELM节点类型转换方案的正确性。

表2 Case 39节点测试系统下的CHELM与NR法电压计算结果对比Table 2 Voltage computational results comparison between CHELM and NR method under Case 39-bus test system
进一步通过Case 118节点测试系统对所提转换方案的通用性进行验证。采用所提CHELM计算的Case 118节点测试系统基态潮流下PV节点无功越限情况如附录B表B2所示,由表可知,节点9、15、16、43、46、48共6个PV节点出现无功功率越限情况,该计算结果与NR法计算结果一致。
首先按照方案1将上述无功越限的PV节点均转换为PQ节点,然后采用CHELM计算系统潮流。附录B表B3对比了所提CHELM与NR法计算得到的所有越限PV节点转换为PQ节点后的电压幅值和相角。由表可知:采用所提CHELM节点转换方案1的计算结果与NR法的计算结果一致,电压幅值和相角的相对误差均为0。在整个潮流计算结果中,CHELM相对于NR法的电压幅值最大绝对误差为3.53×10-6p.u.,电压相角最大绝对误差为1.66×10-4°,验证了所提CHELM节点类型转换方案1的可行性和有效性。
进一步根据所提CHELM的节点类型转换方案2,在每次潮流计算结束后仅对越限量最大的PV节点进行类型转换。附录B表B4对比了采用CHELM节点类型转换方案2的节点转换结果与NR法的节点转换结果。2种方法均依次将节点46、16、43、9、48、15转换为PQ节点,共经过6次节点类型转换得到最终的潮流解。附录B表B5进一步对比了2种方法计算的所有发生节点类型转换的节点电压幅值和相角。由表可知:所提CHELM节点类型转换方案2所得各无功越限节点的电压计算结果与NR法的电压计算结果一致,电压幅值和相角的相对误差均为0。在所有节点电压幅值和相角中,CHELM相对于NR法的电压幅值最大绝对误差为1.56×10-5p.u.,电压相角最大绝对误差为8.23×10-4°,验证了所提CHELM节点转换方案2的正确性和有效性。
上述Case 39和Case 118节点测试系统算例验证了本文所提2种CHELM节点类型转换方案的正确性和可行性,这2种方案可应用于电力系统的潮流求解。
3.2 收敛性分析
本节以Case 2 868rte系统为例,通过潮流计算过程中的最大功率不平衡量ΔS~的变化趋势分析幂级数计算阶数对潮流计算收敛性的影响。
图2对比了传统HELM和CHELM计算该系统潮流时,随着幂级数阶数升高,ΔS~中最大不平衡量的变化趋势(图中纵轴均为标幺值)。图2(b)中横轴“12(0)”表示所提CHELM每计算12阶(nmax=12)后更新常项值,将阶数初始化为0。由图2可知:在传统HELM幂级数阶数达到27阶后,便达到最高计算精度,但也仅为10-2;而在CHELM更新2次常项值后,计算精度就达到了10-3。进一步由图2可看出:在传统HELM达到最高精度10-2后,功率不平衡量一直呈现出较高幅值的振荡,计算精度难以进一步提高,观察发现,在计算过程中幂级数系数呈递增趋势,当幂级数阶数增至50时,幂级数系数升至1018数量级,幂级数系数过大且阶数过高,导致解析延拓发散,影响电压逼近值的计算,进而影响功率的计算结果,使得功率不平衡量ΔS~持续振荡,最终导致潮流计算发散;而在本文所提CHELM计算精度达到10-3后,ΔS~经过极小幅度的振荡后逐渐减小,直至达到10-11,在第1次更新常项值后,幂级数系数即降至10-3数量级,解析延拓可较好地收敛至电压逼近值,进而可保证准确求解出系统潮流解,实现潮流计算的快速收敛。
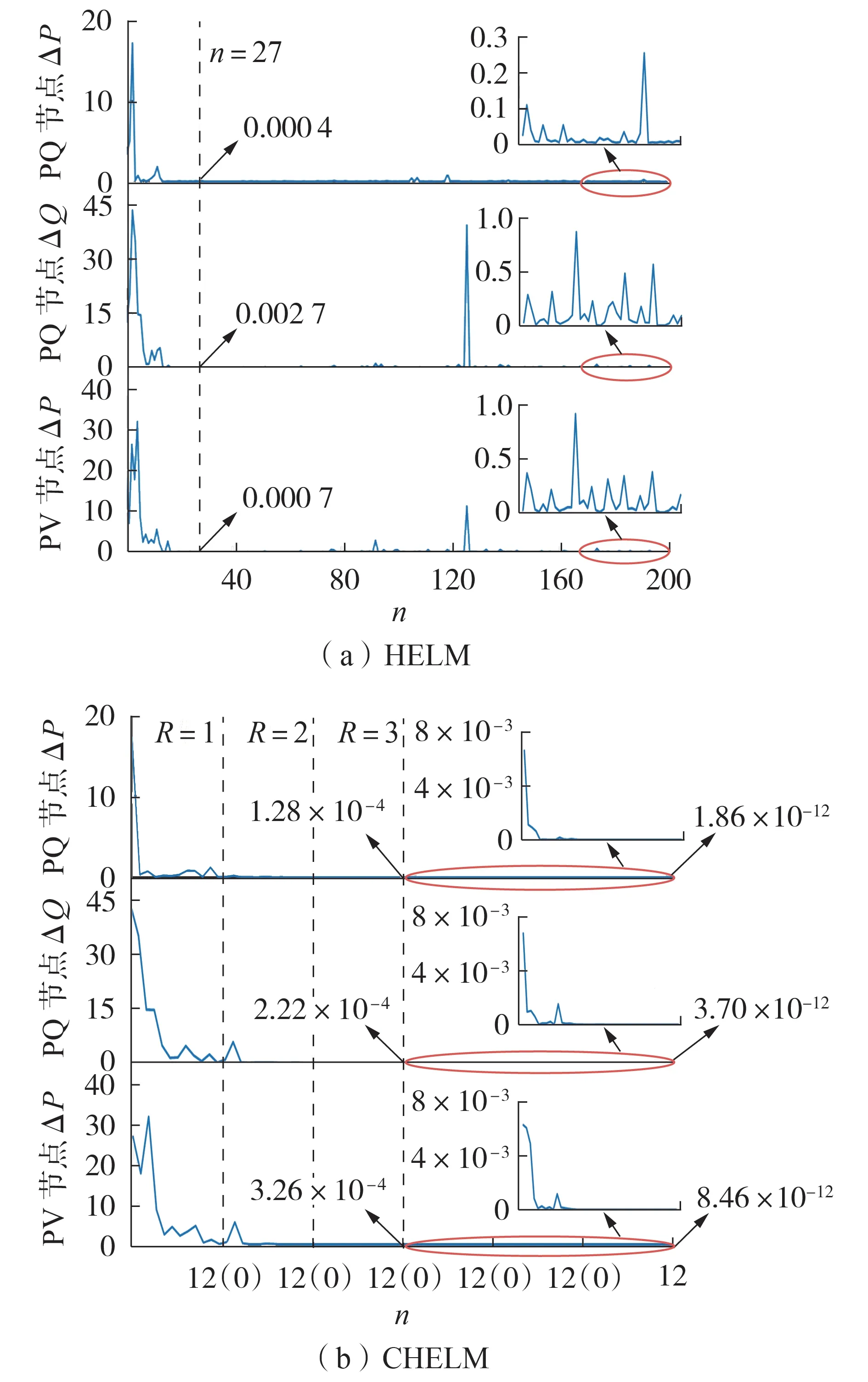
图2 Case 2 868rte测试系统下传统HELM与所提CHELM功率不平衡量变化趋势对比Fig.2 Unbalanced power change trend comparison between traditional HELM and proposed CHELM under Case 2 868rte test system
综上:在利用传统HELM求解系统潮流时,功率不平衡量持续振荡,将导致潮流计算发散;而在利用所提CHELM计算系统潮流时,由于动态更新常项值后,幂级数系数有效降低且呈下降趋势,可使解析延拓较好地收敛,且随着阶数升高,计算过程中的不平衡量仅存在较小幅值的振荡,整体呈下降趋势,最终可使潮流收敛至精确解附近,保证了潮流计算的收敛性和准确性。
3.3 计算效率对比
3.3.1 常项值对计算效率的影响分析
表3对比了传统HELM和所提CHELM在求解部分系统潮流时的计算耗时。由表可知,引入所提动态更新常项值的计算策略后,CHELM计算效率明显高于传统HELM,计算效率提升大于34 %,平均提升了45.79 %,计算耗时显著缩短。这是由于HELM仅以1个固定的幂级数常数项作为计算初始点,不断更新幂级数高阶项系数,进而求取各节点电压值,计算效率较低,而本文所提CHELM在每达到所设定的幂级数阶数上限nmax时就更新常项值,求解过程更灵活,不仅可保证解析延拓具有较好的收敛性,而且可更快求得电压解,显著缩短了全纯嵌入潮流计算耗时。

表3 传统HELM与CHELM计算耗时对比Table 3 Computational time comparison between traditional HELM and CHELM
综上,在传统HELM中引入本文所提更新常项值的计算策略后,不仅可以解决大规模系统的全纯嵌入潮流收敛问题,极大提高HELM收敛性,而且可进一步提升计算效率,实现电力系统潮流的快速求解。
3.3.2 先验节点对计算效率的影响分析
本节验证采用先验节点电压幅值预判提升所提CHELM计算效率的有效性。附录B表B6对比了CHELM与P-CHELM求解部分系统的计算耗时。由表可知,采用先验节点电压幅值的预判策略可进一步提升HELM效率,计算效率最低提升了17 %,平均提升了24.50 %。因此,引入所提先验节点的计算策略,可减少不必要的计算冗余,有效提高CHELM的计算效率。
为体现本文所提方法的计算效率,附录B表B7对比了所提P-CHELM和传统HELM对部分1 000~25 000节点测试系统的潮流计算耗时。由表可知,所提P-CHELM计算效率远高于传统HELM,效率提升高达49.55 %~64.74 %,平均提升了58.66 %。综上,相较于传统HELM,本文所提方法不仅收敛性好以及计算精度高,而且具有更高的计算效率。
3.4 鲁棒性对比
本节对比CHELM与平启动下NR法的收敛性和计算耗时。NR法最大迭代次数设为10次。
NR法采用平启动时,300节点及以下规模的系统均可有效收敛,计算耗时与CHELM的结果对比如附录B表B8所示。由表可知,对于小规模系统,在保证计算准确性的前提下,CHELM的计算效率接近NR法。
对于1 000节点以上的大规模系统,P-CHELM与NR法的计算耗时如表4所示。由表可知,随着系统规模的增大:NR法采用平启动时,收敛性问题愈发严重;而所提P-CHELM仍能保持全纯嵌入潮流求解的特性,在保证计算结果准确性和精度的前提下,表现出良好的收敛性。

表4 P-CHELM与NR法计算耗时对比Table 4 Computational time comparison between P-CHELM and NR method
综上,本文所提P-CHELM对不同规模电力系统的潮流计算均可收敛,相较于NR法具有更强的鲁棒性。
4 结论
本文提出P-CHELM,通过节点数在4~25 000之间不同规模的电力系统测试系统算例对其进行分析、验证,得到结论如下:
1)所构建全纯嵌入潮流模型以及节点类型转换方案合理、可行,可实现基于常项值的实际电力系统全纯嵌入潮流准确、快速计算;
2)所提CHELM可解决传统HELM中解析延拓的收敛问题,具有更好的潮流收敛性能和更高的计算精度;
3)所提常项值动态更新策略和先验节点电压幅值预判机制可有效降低全纯嵌入潮流的计算量,在保证计算准确性的前提下,有效提高了计算效率;
4)与NR法相比,所提P-CHELM不依赖于初值便可准确、快速计算出系统潮流解,其收敛性更强,为新型电力系统的潮流计算提供了新思路。
需指出的是,尽管所提方法相较于传统HELM和NR法均具有更强的潮流收敛性,且相较于传统HELM具有较高的计算效率,但是其计算时间仍有进一步的优化空间,而如何在本文基础上继续提高全纯嵌入潮流的计算效率,将是笔者后续研究的重点。
附录见本刊网络版(http://www.epae.cn)。
