基于负载变流器控制带宽的直流系统稳定性分析
2023-02-27赵学深李霞林王成山
卢 浩,朱 琳,赵学深,郭 力,李霞林,王成山
(1. 智能电网教育部重点实验室(天津大学),天津市 300072;2. 天津市智慧能源与信息技术重点实验室,天津市 300072)
0 引言
直流系统相对于交流系统在低碳和灵活性方面具有明显优势,其控制简单,无须考虑频率、相角及同步等问题,有利于新型电力电子化源荷的接入[1-2],有助于增加可再生能源的利用率并提高系统效率,是未来智能配电系统的重要组成部分[3-4]。但是,由于其具有拓扑结构灵活、运行状态多且低碳电力电子源荷随机性波动性强等特点,直流系统的稳定性问题是研究中关注的重点[5-7]。
源侧输出阻抗与负载侧输入阻抗比不满足奈奎斯特判据是互联系统不稳定的根源[8-9]。故对于不稳定的互联系统,一般采用调整源侧输出阻抗或改变负载侧输入阻抗的方法使得源载阻抗比满足奈奎斯特判据,保证系统稳定。调整源侧输出阻抗的方法可分为无源[10-11]和有源[12-13]。无源方法通常在电路中加入电阻、电容或电感器件,其中,文献[14]在源侧变流器的直流稳压电容后并联了一个RC 和RL 滤波器来减小输出阻抗的振荡尖峰,保证了系统的稳定性,但无源器件同时带来了较大的功率损耗。与无源方法相比,有源方法仅用控制算法来调整源侧输出阻抗。文献[15]提出了基于低通滤波的有源阻尼方法,减小了源侧变流器的等效输出阻抗,解决了由线路电抗与变流器稳压电容构成的低阻尼LC 环节导致直流微电网发生高频振荡的失稳现象。文献[16]针对线路引起中压直流系统直流侧容易发生高频振荡的问题,提出了一种正阻尼重构稳定控制策略,调整了源侧输出阻抗的相位,使线路中的电感与变流器的输入滤波电容构成的LC 振荡环节与源侧输出阻抗耦合区域的相位大于−90°,使得源侧输出阻抗在LC 振荡频率附近呈现正阻尼特性,抑制了含线路的输出阻抗振荡尖峰,提高了系统的稳定性。然而,调整源侧输出阻抗的方法具有一定的局限性:
1)当系统拓扑改变时,如系统运行工况改变(开环、合环运行)、增加负载等,均需重新设计源侧变流器控制参数,不利于系统多工况无缝切换的稳定安全运行;
2)需要获取系统全部参数且对精度要求较高,在系统参数不确定性较强的情况下,通过源侧变流器控制解决稳定性问题可能导致系统不能达到预期带宽阻尼,使整个系统失稳。
为了降低对系统拓扑及全局参数信息的依赖性,文献[17-19]研究了通过改变负载侧输入阻抗确保系统稳定的方法。文献[17]在负载变流器比例-积分(PI)控制回路中引入母线电压来调节负载变流器的占空比,在非常小的频率范围内增大负载变换器的输入阻抗,抑制了源载交互引发的振荡。文献[18]在负载变流器的PI 控制回路中引入母线电流来调节负载变流器的占空比,同样增大了负载变换器的输入阻抗。上述方法均需要在负载侧控制环节中增加额外的控制环,不能只使用市场产品的通用PI 控制算法,难以推广应用。此外,将线路阻抗与源侧输出阻抗并联的阻抗模型仅适用于级联系统,对于共母线直流系统并不适用。
针对上述问题,本文基于通用PI 控制器,不增加额外控制环,无需整个系统的全局信息,通过限制负载侧PI 参数选取的范围改变负载变流器输入阻抗,解决了负载变流器经线路聚合至共母线直流系统发生的非预期失稳问题。最后,通过硬件在环仿真实验验证了负载子系统自稳性判据的正确性。
1 系统结构及建模
本文以图1 所示的共母线直流系统电路模型为对象开展理论研究,其共母线直流系统结构如附录A 图A1 所示。模型主要由3 个部分组成:1)AC-DC变流器作为外部交流网与共母线直流系统的能量转换接口;2)通过源侧DC-DC 变流器向375 V 直流母线供电;3)多种类型的N台负荷变流器通过直流线路接入共母线直流系统。图1 中:iLs、io、Vs、Vbus分别为源侧变流器电感电流、输出总电流、输入电压和母线电压;Cs和Ls分别为直流母线电压变流器的出口侧稳压电容和滤波电感;Lline,m、Rline,m、CinCPL,m、RCPL,m、CCPL,m、LCPL,m分别为第m台负载变流器接入母线的线路电感、线路电阻、输入滤波电容、低压侧负载阻抗、出口侧稳压电容和滤波电感,其中,m=1,2,…,N,N为负载变流器数量。

图1 共母线直流系统电路模型Fig.1 Circuit model of DC system with common bus
源侧变流器和负载变流器的控制框图如附录A图A2 所示。图中:kP,v和ki,v分别为源侧变流器电压环的比例系数和积分系数;kP,i和ki,i分别为源侧变流器电流环的比例系数和积分系数;Vrefb和ds分别为母线电压参考值和源侧开关管占空比;kP,CPL,m和ki,CPL,m分别为第m台负载变流器电压环的比例系数和积分系数;VCPL,m、VCPL,m,ref、dCPL,m分别为第m台负载变流器的输出电压、输出电压参考值、占空比。
1.1 恒功率负载阻抗模型
在对负载变流器进行建模时,图1 紫色框中第m台负载变流器的输入阻抗通常被等效成−V2inCPL,m/PCPL,m的通用负增量阻抗模型,其中VinCPL,m和PCPL,m分别为第m台负载变流器的输入电压和额定功率。然而在考虑负载变流器控制参数的影响时,需对其建立恒功率负载阻抗ZCPL,m(s)的模型[19],可表示为:

ZCPL,m(s)的阻抗特性如图2 所示。

图2 ZCPL,m(s)的Bode 图Fig.2 Bode diagram of ZCPL,m(s)
图2 中,fCPL,m为第m台负载变流器的控制带宽(表达式见附录A 式(A1)),其对应相角为−90°,此时:

式中:Re(∙)表示阻抗值的实部。
ZCPL,m(s)与通用负增量阻抗模型相似之处在于:当 频 率f
1.2 负载子系统模型——计及线路影响的恒功率负载模型
负载变流器通过线路连接至共母线直流系统,其中线路阻抗采用π 型模型。由于线路分布电容远小于负载变流器输入滤波电容,因此忽略线路分布电容的影响。第m台负载变流器计及线路影响的恒 功 率 负 载ZPOL,m(s)由ZCPL,m(s)、Lline,m、Rline,m和CinCPL,m组 成,如 图1 黄 色 框 所 示。ZPOL,m(s)的 表 达式为:

式中:“//”表示并联。
1.3 负载侧总并联输入阻抗和源侧总输出阻抗模型
结合图1 蓝色框和式(3),得到负载侧总并联输入阻抗ZPOL(s)为:

共母线直流系统源侧总输出阻抗Zout(s)如图1橙色框所示,其表达式详见附录B 式(B3)。由式(4)和 式(B3)可 得,系 统 源 载 阻 抗 比To(s)=Zout(s)/ZPOL(s)。从To(s)可以看出,使系统满足奈奎斯特判据可以:1)减小Zout(s);2)增大ZPOL(s)。由于本文在负载侧解决系统稳定性问题,下面将分析负载变流器控制带宽对系统稳定性的影响。
2 恒功率负载控制带宽对系统稳定性影响的分析
通常情况下,源侧变流器或负载变流器在设备出厂前,都会基于该台变流器在其独立运行时的传递函数模型,按照通用控制带宽选取原则设计其控制参数(变流器电压环控制带宽通常不超过该变流器开关频率的1/10),以满足稳定性需求。但当负载变流器通过线路聚合至共母线直流系统时,由于Lline,m与CinCPL,m形成了LC 电路谐振,可能会导致系统振荡失稳,现以附录B 表B1 所示共母线直流系统为例进行说明。附录A 图A3 为负载变流器在不同控制带宽下(fCPL,m取值范围为200~500 Hz,开关频率fkCPL,m为5 000 Hz),以频率和幅值平面构成的ZCPL,m(s)与Zout(s)的Bode 图。
由式(1)、附录B 式(B3)和附录A 图A3 可知,fCPL,m的改变仅改变了ZCPL,m(s),并不影响Zout(s),因此在不同fCPL,m下,Zout(s)均相同。显然,在没有任何线路连接时,每一个fCPL,m下ZCPL,m(s)与Zout(s)在频率和幅值构成的平面内均满足Zout(s) 但当负载变流器通过线路聚合至共母线直流系统 时,Lline,m与CinCPL,m构 成 的LC 环 节 会 与ZCPL,m(s)相互影响,可能导致共母线直流系统发生振荡失稳。附录A 图A4 为负载变流器控制带宽fCPL,m分别为200、250、400、500 Hz 时To(s)的奈奎斯特曲线。 由 附 录A 图A4 可 知,随 着fCPL,m的 增 加,To(s)的奈奎斯特曲线向点(−1,j0)移动,系统稳定裕度逐渐减小,特别是当fCPL,m=500 Hz 时,奈奎斯特曲线包含了点(−1,j0),不满足奈奎斯特判据,系统会失去稳定。由To(s)=Zout(s)/ZPOL(s)可知,在不调整Zout(s)的情况下,改变fCPL,m影响了ZPOL,m(s),进而影响了整个系统稳定性。图3 为不同负载变流器控制带宽下ZPOL,m(s)的Bode 图。 图3 不同fCPL,m下ZPOL,m(s)的Bode 图Fig.3 Bode diagram of ZPOL,m(s) with different fCPL,m 由图3 可知,Lline,m与CinCPL,m构成的LC 环节会与ZCPL,m(s)相互作用,使得计及线路影响的ZPOL,m(s)在LC 振 荡 频 率fline,m(即1/(2πCinCPL,m Lline,m)≈237 Hz)处产生振荡尖峰。此外,ZPOL,m(s)的相位在fline,m附近急剧变化,当fCPL,m较小时,ZPOL,m(s)在振荡频率的相位在−90°到0°之间,此时ZPOL,m(s)的阻抗呈正阻尼特性;随着fCPL,m的增加,ZPOL,m(s)在振荡频率的相位在90°到180°之间,此时ZPOL,m(s)的阻抗恶化成负阻尼特性,系统稳定性降低。对比附录A 图A4 和图3 可知,随着负载变流器控制带宽的增大,负载变流器经线路聚合至共母线直流系统发生了非预期的失稳现象,根本原因为线路电感与变流器输入滤波电容构成的LC 环节与ZCPL,m(s)相互作用,使得ZPOL,m(s)在振荡频率处的阻抗为负阻尼,恶化了系统的稳定性。所以,通过合理控制负载变流器带宽,可确保ZPOL,m(s)在振荡频率处的阻尼为正,保障系统的稳定性。 本章将分析在振荡频率处ZPOL,m(s)的阻抗,从而揭示负载变流器及其线路间的相互作用影响共母线直流系统稳定性的机理。 附录A 图A5 为ZPOL,m(s)的电路拓扑结构。其中,振荡频率fline,m的表达式为: 为了更为清晰直观地理解,接下来将针对振荡频率fline,m位于负载变流器控制带宽内和控制带宽外2 种情况,利用图解法和极限法共同确定ZPOL,m(s)在振荡频率处的阻抗值。 当振荡频率fline,m位于负载变流器控制带宽内(fline,m 当频率f→0 时,ZPOL,m(s)的示意图如附录A 图A6(a)所示。结合式(5),将s=j2πfline,m代入式(7),此 时 在 振 荡 频 率 处ZPOL,m(s) 的 阻 抗 值ZPOL,m(j2πfline,m)记为M1: 在振荡频率fline,m位于负载变流器控制带宽外(fCPL,m 因此,当振荡频率fline,m位于负载变流器控制带宽内(ZCPL,m(s)负阻尼区)时,在fline,m处线路的正电阻Rline,m与ZCPL,m(s)的负阻抗相抵后,ZPOL,m(s)阻抗减小,在ZCPL,m(s)的负阻抗过大时,甚至会使ZPOL,m(s)在振荡频率处阻尼为负,导致系统稳定性恶化;反之,当fline,m位于负载变流器控制带宽外(ZCPL,m(s)正阻尼区)时,在fline,m处ZPOL,m(s)阻抗始终保持正阻尼特性,且阻抗值恒大于Rline,m。依据Bode 图和奈奎斯特判据,当系统同时满足:1)存在负阻尼环节;2)Zout(s)和ZPOL(s)幅值曲线相交处,Zout(s)和ZPOL(s)的 相 角 差 大 于180°,系 统 不 稳定[20-21]。由上述分析可知,负载变流器控制带宽小于线路振荡频率时,ZPOL,m(s)在fline,m处的阻抗为正阻尼,此时Lline,m与CinCPL,m构成的LC 环节与ZCPL,m(s)的相互作用并没有为系统带来额外的负阻尼,在原系统稳定的前提下,接入满足带宽要求的ZPOL,m(s),系统同样保持稳定,详细推导见附录C。 基于上述分析,本文提出负载子系统自稳性判据,用于判别负载变流器经线路聚合至共母线直流系统后发生的非预期失稳问题。其判据表达式为: 当所接入共母线直流系统负载变流器的带宽与其线路振荡频率满足式(16)时,系统满足奈奎斯判据,保证了系统稳定。 为了验证所提判据的有效性,在附录B 图B3 所示的LaunchXL-F28069M 控制板和实时数字仿真RT-BOX 平台进行了控制硬件在环实验。 现以附录B 表B1 所示的单源单负载共母线直流系统为例,进行理论分析和实验验证。负载变流器1 的开关频率为5 kHz,其控制带宽fCPL,1初始值为419 Hz,经线路连接至共母线直流系统,由式(5)可得振荡频率fline,1≈237 Hz。 实验中负载变流器1 以功率PCPL,1=180 kW 向直流负荷供电,某时刻PCPL,1从180 kW 增加到200 kW。由图4(a)可知,由于fline,1 图4 案例A 系统频域分析图和直流母线电压实验结果波形Fig.4 Diagrams of system frequency domain analysis and experimental result waveforms of DC bus voltage in case A 基于式(16)调整fCPL,1 现以附录B 表B2 所示的单源多负载共母线直流系统为例,开展理论分析和实验验证工作。在实验过程中,负载变流器1 以功率PCPL,1=300 kW 向直流负荷供电,负载变流器2 以功率PCPL,2=180 kW 向直流负荷供电,某时刻负载变流器2 的PCPL,2从180 kW 增加到200 kW。负载变流器1 的带宽为fCPL,1=200 Hz,fline,1=237 Hz,即fCPL,1 图5 案例B 系统频域分析图和直流母线电压实验结果波形Fig.5 System frequency domain analysis diagrams and experimental result waveforms of DC bus voltage in case B 负载变流器2 的开关频率为10 kHz,由图5 系统频域分析图可知,负载变流器2 的初始控制带宽fCPL,2为760 Hz(fline,2 基于式(16)调整fCPL,2为180 Hz,fCPL,2 上述理论及实验结果均证明了负载子系统自稳性判据的有效性。 本文开展了负载变流器控制带宽影响系统稳定性的理论研究和实验验证。主要结论如下: 1)源-载变流器基于开关频率设计控制参数合理,而负载变流器经线路聚合至共母线直流系统后却发生振荡失稳现象的根本原因是线路电感与负载变流器输入滤波电容构成的LC 振荡环节相互作用,使得计及线路影响的恒功率负载在振荡频率处的阻尼为负,恶化了系统的稳定性。 2)基于推导计及线路影响的恒功率负载在振荡频率处的阻抗可知,当线路振荡频率小于负载变流器控制带宽时,振荡尖峰落入恒功率负载阻抗负阻尼区域,使得计及线路影响的恒功率负载在振荡频率处的阻抗值可能呈现负阻尼特性,导致系统稳定性变差;反之,落入正阻尼区域,振荡频率处的阻抗值恒大于线路电阻值,为正阻尼特性,保证了系统的稳定性。 3)提出了一种负载子系统自稳性判据,仅通过比较线路电感与负载变流器输入滤波电容构成的LC 振荡频率与负载变流器的控制带宽的大小,能够有效解决负载变流器经线路聚合至共母线直流系统发生的非预期失稳问题。 值得注意的是,本文提出的负载子系统自稳性判据给出了在保证全直流系统稳定的情况下,负载变流器控制带宽选择的上限,然而并非控制带宽选择越小越好。负载变流器控制带宽越小,全系统的阻尼虽然会越好,但是负载本身的响应速度也会变慢,故负载变流器控制带宽的优化选择将是后续研究的重点。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。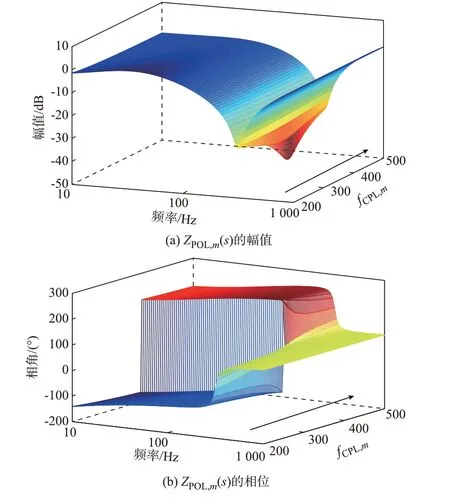
3 负载子系统自稳性判据






4 理论分析与实验验证
4.1 案例A:级联系统

4.2 案例B:单源多负载系统

5 结语
