基于指数变换的电力系统不稳定特征值计算方法

陈亦平，曹玉磊，赵利刚，肖 亮，李崇涛

（1. 中国南方电网电力调度控制中心,广东省广州市 510663；2. 中国南方电网科学研究院有限责任公司,广东省广州市 510663）

0 引言

特征分析法是电力系统小干扰稳定性分析过程中的一个有效方法［1］。其中,QR/BR 等全特征值计算方法具有数值稳定性好、收敛速度快且不漏根的优势［2］。然而,随着现代电力系统规模的不断扩大,系统状态变量的数量可以达到几千阶甚至数万阶,全特征值计算方法已经不能满足大规模系统特征分析的需要。在小干扰稳定分析过程中,通常只有部分关键特征值是所关心的。因此,部分特征值计算方法成为进行大规模电力系统小干扰稳定性分析的切实可行方法。其中,电力系统小干扰稳定分析中关键特征值通常可以分为两类［3］,即弱阻尼特征值和不稳定特征值。

目前,部分特征值计算方法包括序贯法、子空间法［4］。其中,利用子空间法可以得到系统的一组模值最大的特征值。子空间方法中最具有代表性的是基于Krylov 子空间的隐式重启动Arnoldi（implicitly restarted Arnoldi,IRA）方法［5-7］、基于非Krylov 子空间的Jacobi-Davidson（JD）方法［8］和子空间加速瑞利商迭代方法［9］。

IRA 方法具有算法适应性强、收敛速度快的优点,是求解电力系统部分特征值最成功的方法之一,已经被国内外多种电力系统特征值计算程序和小干扰分析程序采用,如PEALS、PSAT 和PSASP等［10］。该方法的主要特征是可以优先收敛到模值最大的特征值,在实际应用中需要配合位移-逆变换或者Cayley 变换将关键特征值映射为模值最大的主导特征值［11］。因此,通过在弱阻尼区域设置一系列的位移点,便可以得到几乎所有的弱阻尼特征值。但位移-逆变换或者Cayley 变换在求解不稳定特征值时性能并不好［12］。这是因为特征值的主导性随着离位移点的距离增加而减弱,而不稳定模态在右半平面上的分布无法提前估计。

作为以上特征值计算方法的补充,本文提出一种基于指数变换的双层Arnoldi 算法来求解大规模电力系统的不稳定特征值。首先,该方法采用了一种指数变换的谱变换方式。由于指数变换在求解不稳定特征值时具有良好的谱主导性和谱稀疏性,因此所提方法可以不遗漏地求解电力系统的全部不稳定特征值。此外,本文采用了内层Arnoldi 算法隐式地求解指数矩阵与向量的乘积,避免了显式计算指数矩阵,使得所提方法在保证计算精度的前提下具有较高的计算效率,从而可以满足在大规模实际系统中应用的需要。

1 小干扰稳定性分析基础

1.1 数学模型

电力系统的小干扰稳定性分析的数学模型通常可以用如下微分代数方程来描述:

式中:A͂∈Rn×n、B͂∈Rn×m、C͂∈Rm×n、D͂∈Rm×m为稀疏矩阵,其中n为状态变量Δx的个数,m为代数变量Δy的个数。

消去式（1）中代数变量Δy,得到:

式中:A∈Rn×n为系统的状态矩阵,其具体形式如式（3）所示。

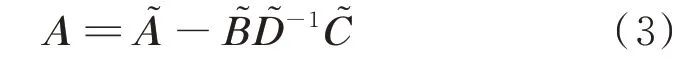
需要说明的是,状态矩阵A失去了稀疏特性。在实际计算中,关于状态矩阵A的所有运算都采用稀疏技术［13］,而不直接计算A。在本文中,为了叙述方便,算法中仍然采用A来描述。

1.2 关键特征值分类

电力系统小干扰稳定分析中关键特征值所在区域通常可以分为弱阻尼区域和不稳定区域［3］,如图1所示。

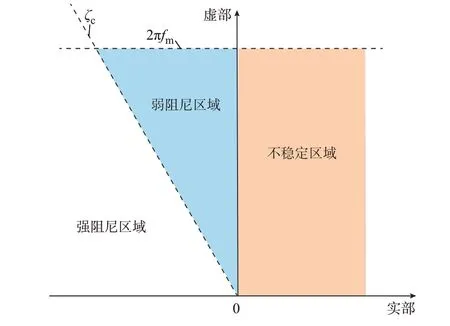
图1 关键特征值所在区域分类Fig.1 Region classification of critical eigenvalues

从图1 可以看出,弱阻尼区域是由关键阻尼比ζc、虚轴以及最大振荡频率fm所决定的窄三角区域。除此之外,另一个区域为位于虚轴右侧的不稳定区域。在实际电力系统中,控制器参数调节不恰当可能会导致电力系统出现不稳定特征值。而遗漏其中任何一个不稳定特征值都将导致对电力系统的小干扰稳定性产生错误的判断。因此,本文提出了一种双层Arnoldi 算法来求解电力系统的全部不稳定特征值。

2 外层隐式重启动Arnoldi 算法

本章首先回顾了基本的Arnoldi 方法；然后,给出了指数变换的定义；最后,基于指数变换给出了计算电力系统不稳定特征值的外层Arnoldi 算法和相应的隐式重启动策略。

2.1 基本的Arnoldi 方法

给定一个矩阵M∈Rn×n和一个初始非零向量v∈Rn,则k阶的Krylov 子空间可以表示为:

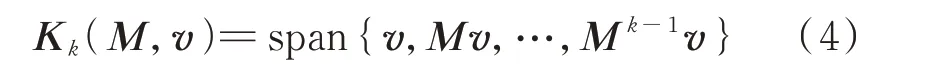
矩阵M关于向量v的k阶Arnoldi 分解具有如下形式:

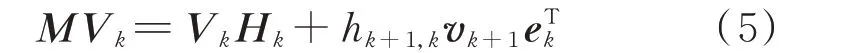
2.2 指数变换

指数变换的定义如下:

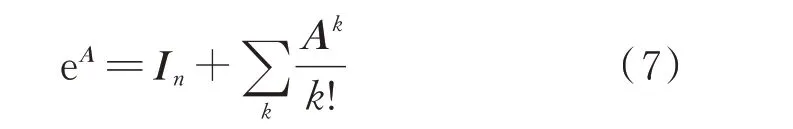
式中:In∈Rn×n为单位矩阵。假设A是可对角化的,那么可以得到状态矩阵A和指数矩阵eA的特征值对之间的对应关系。如果(λ,u)是A的一个特征值对,那么(μ,u)将是eA的一个特征值对,且满足:

相反,如果(μ,u)是eA的一个特征值对,那么(λ,u)是A的一个特征值对,且满足:

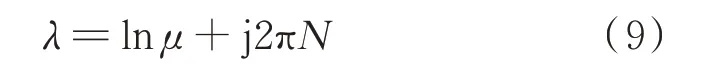
式中:N为参数,是一个具体的正整数。

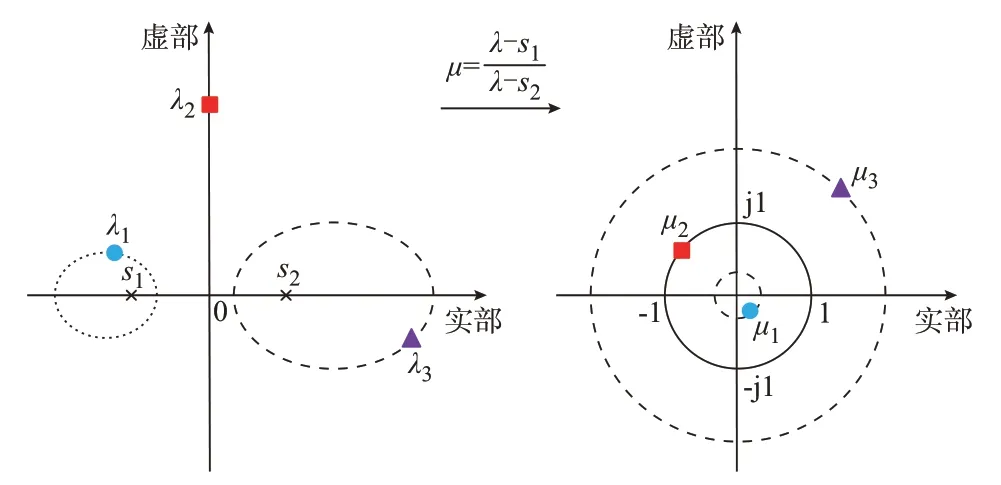
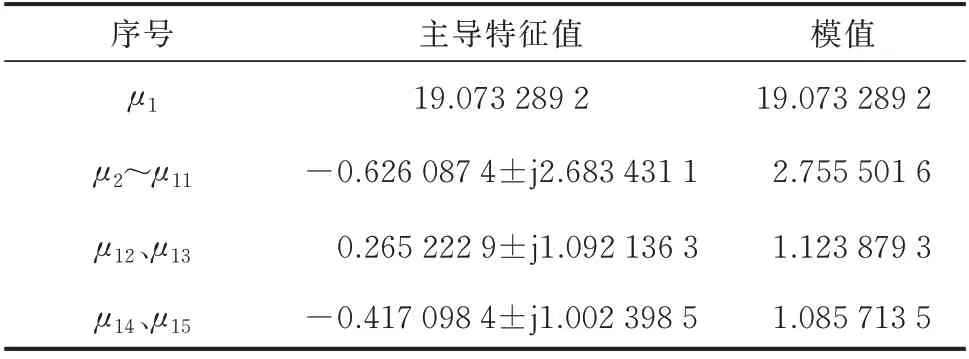
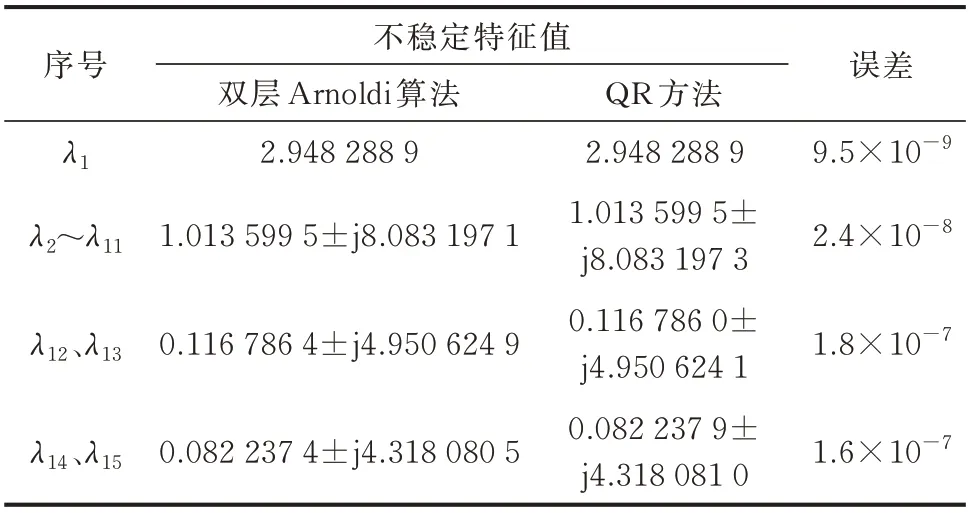
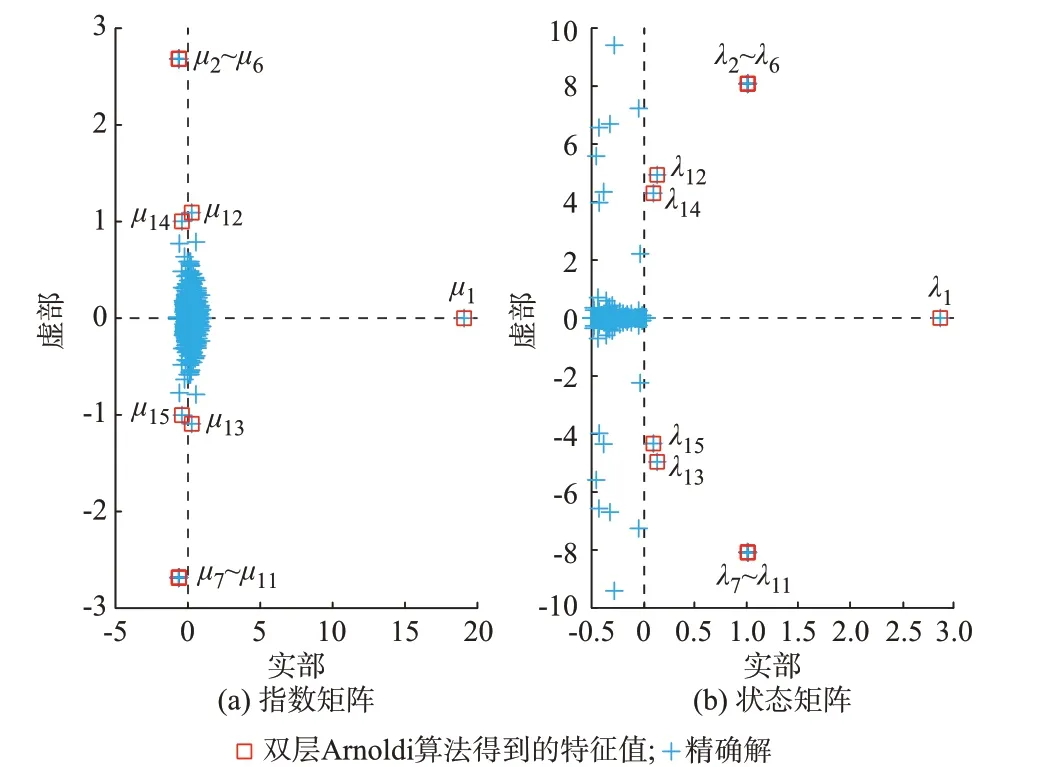
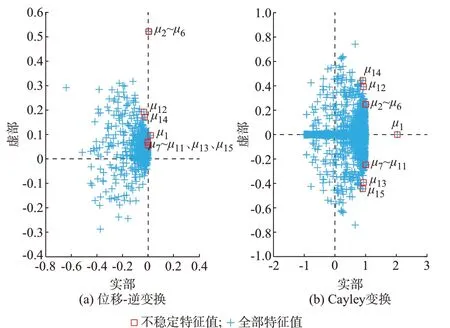
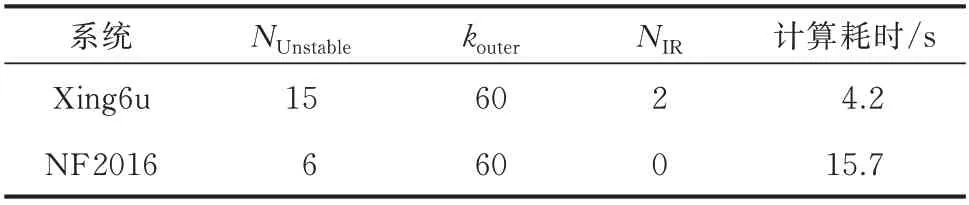
从谱变换的角度来看,指数变换将状态矩阵A的不稳定特征值映射为指数矩阵eA的模值大于1 的主导特征值,如图2 所示。Re(λ2)

图2 指数变换示意图Fig.2 Schematic diagram of exponential transformation

作为对比,Cayley 变换的示意图如图3 所示。可以看出,Cayley 变换也可以将不稳定特征值映射为模值大于1 的特征值,但这种变换降低了映射后特征值之间的距离,使得不稳定特征值收敛较为困难［12］。

图3 Cayley 变换示意图Fig.3 Schematic diagram of Cayley transformation

2.3 重启动策略

Krylov 子空间方法的特征是其可以优先收敛到模值最大的特征值。在外层Arnoldi 算法中,令

也就是对指数矩阵eA进行Arnoldi 分解,然后便可以得到其主导特征值。逆变换后便可以得到状态矩阵A的不稳定特征值。

2.3.1 逆变换求解参数N

假设(μi,ui)是M的一个收敛的特征对,那么需要计算式（9）中的N值来得到对应的特征值λi。考虑到特征值收敛时误差ri的值已经非常小,根据式（9）可以得到:

式中:Round(·)为取整函数；H 表示共轭转置。得到N后,λi=lnμi+j2πN,λi和ui分别为状态矩阵A的特征值和特征向量。

2.3.2 重启动策略

当得到矩阵M关于式（5）的Arnoldi 分解后,如果此时主导特征值并没有全部收敛,就需要采用重启动策略来提高特征值的收敛性。对Hk的特征值按模值递减排序,即

此外,在利用外层隐式重启动Arnoldi 算法求解状态矩阵A的不稳定特征值的过程中,需要计算指数矩阵eA与向量v的乘积。考虑到直接求解大规模指数矩阵eA是不现实的,下面采用内层Arnoldi 算法来隐式求解eAv。

3 内层采用加速收敛技术的Arnoldi 算法

3.1 内层Arnoldi 算法求解eAv

本节利用Arnoldi 算法隐式地求解eAv的值［14］。给定状态矩阵A和向量v（其中||v||2=1）,则k阶的Krylov 子空间可以表示为:

3.2 加速收敛技术

实际的电力系统通常为刚性系统,也就是同时存在模值很大和模值很小的特征值,这会导致内层Arnoldi 算法的收敛速度很慢［16］。因此,为了提高Arnoldi 算法的收敛速度,本节采用基于位移逆矩阵S的加速收敛技术［15-16］。位移逆矩阵S定义为:

式中:τ为位移系数,通常取值为很小的正实数,如0.02。

相应的Arnoldi 分解具有如下形式:

如果误差rk小于收敛容差εinner,那么VkeGke1可以被认为是eAv的一个很好的近似解。需要说明的是,eGk是一个低阶指数矩阵,可通过文献［17］中的算法高效求解。

3.3 求解eAv 的算法流程

利用内层Arnoldi 算法求解eAv流程如下:

步 骤1:给 定A、v、εinner、kinner,其 中kinner为 内 层Arnoldi 算法的最大扩展维数,令M=S。

步骤2:令k=1,2,…,kinner,根据式（25）得到k阶Arnoldi 分 解,根 据 式（31）计 算 误 差rk,若rk<εinner,结束迭代。

步骤3:根据式（29）计算得到eAv。

在步骤2 的Arnoldi 分解过程中,需要计算Sv的值,为了减小计算量,这里采用稀疏技术而不直接计算状态矩阵A［13］。此外,考虑到Arnoldi 分解的阶数k较小时误差rk通常较大,为了减小计算量,可以当k较大（k>40）时再计算误差rk。

4 算法实现

利用双层Arnoldi 算法求解电力系统不稳定特征值的算法流程如下:

步 骤1:给 定A、v、kouter、εouter,其 中kouter为 外 层Arnoldi 算 法 的 维 数,εouter需 要 设 定 的 比εinner小。令v←v/||v||2。

步骤2:形成矩阵eA的kouter阶Arnoldi 分解,其中eAv的计算利用内层Arnoldi 算法实现。

步骤3:计算得到Hk的所有特征值对(μi,zi),i=1,2,…,kouter,然后对特征值μi按式（13）进行排序。

步骤4:令q为模值大于1 的特征值μi的数量,根据式（6）判断前q个特征值μi是否收敛。如果收敛,则结束迭代,转向步骤6。

步骤5:令前p（p>q）个特征值为期望特征值,根据式（16）得到前p阶Arnoldi 关系,然后扩展到kouter阶Arnoldi 分解,转向步骤3。

步骤6:根据式（9）采用逆变换,得到状态矩阵A的所有不稳定特征值。

考虑到实际系统中由于控制器参数设置不合理等因素产生的不稳定特征值数目较少,kouter设置为60 就已足够。重启动过程中期望特征值的个数p需要设定的比q略大。

5 算例分析

本文利用Xing6u 和NF2016 这2 个实际系统来验证所提方法的有效性。其中,Xing6u 是开源的系统［9］,NF2016 是 以 中 国 某 区 域 电 网2016 年 运 行 方式为基础的实际系统。Xing6u 系统有2 940 个状态变量、17 798 个代数变量、73 946 个非零元素。NF2016 系 统 有40 819 个 状 态 变 量、71 656 个 代 数 变量、486 605 个非零元素。本文所进行的测试都是在一台装有Intel i7 CPU、内存为16 GB 的台式机上进行的,并且所有测试都用C++代码编写。

5.1 不稳定特征值计算

首先,在Xing6u 和NF2016 这2 个系统上测试内层Arnoldi 算法的有效性。任取初始向量v,随着内层Arnoldi 算法维数的扩展,根据式（31）得到计算eAv时的误差。当eAv的计算精度为10-8时,Arnoldi分解的维数通常小于60,即内层Arnoldi 算法可以快速且准确地求解eAv。因此,收敛容差εinner可以设置为10-8。对于极少数初始向量v,当扩展维度小于80 时,内层Arnoldi 算法可能收敛不到10-8。此时,为了提高计算效率,可以选取最小误差时对应的维度来求解eAv。此外,为了减小计算量,可以当内层Arnoldi 算法的维数k较大（k>40）时再计算误差rk。

接下来,利用双层Arnoldi 算法计算Xing6u 系统的不稳定特征值。外层Arnoldi 算法的维数kouter设置为60,εouter设置为10-6。经过2 次重启动后,算法2 的迭代终止。指数矩阵eA模值大于1 的主导特征值μ1～μ15如表1 所示。经过逆变换后,状态矩阵A的不稳定特征值如表2 所示。由表2 可以看出,该系统的15 个不稳定特征值λ1～λ15均被得到,包括2.94、0.08±j4.32、0.11±j4.95 以 及5 对 重 特 征 值1.01±j8.08。与QR 方法得到精确解的对比显示,所提方法具有较高的计算精度。

表1 指数矩阵的主导特征值Table 1 Dominant eigenvalues of exponential matrix

表2 状态矩阵A 的不稳定特征值Table 2 Unstable eigenvalues of state matrix A

所得结果与精确解的对比如图4 所示。可以看出,指数映射将所有不稳定特征值映射为模值较大的主导特征值,且不同主导特征值之间的间距较远。因此,利用所提双层Arnoldi 算法非常容易得到系统所有的不稳定特征值。

图4 Xing6u 系统指数矩阵和状态矩阵的特征值分布Fig.4 Distribution of eigenvalues for exponential matrix and state matrix in Xing6u system

最后,为了直观地展示不稳定特征值经过位移-逆变换和Cayley 变换后的分布情况,Xing6u 系统的特征值经过相应变换后的结果如图5 所示。

图5 Xing6u 系统经位移-逆变换和Cayley 变换后的特征值分布Fig.5 Distribution of eigenvalues after shift-invert transformation and Cayley transformation in Xing6u system

位移-逆变换和Cayley 变换的形式分别为A→(A-sI)-1和A→(A-s1I)(A-s2I)-1,其中,s、s1和s2为位移点。在本测试中,采用位移点为s=1+j10 的复位移-逆变换以及位移点为s1=-1和s2=1 的实Cayley 变换。需要说明的是,对于复位移-逆变换来说,只需要关注具有非负虚部的不稳定特征值即可,即图5（a）中的μ1、μ2～μ6、μ12、μ14。

从图5（a）可以看出,在位移-逆变换谱上,靠近位移点s=1+j10 的5 个重特征值成为模值最大的主导特征值。然而,远离该位移点的特征值μ1、μ12、μ14的模值非常小。与位移-逆变换不同,Cayley 变换可以将所有的不稳定特征值映射为模值大于1 的主导特征值。但从图5（b）可以看出,大多数不稳定特征值尤其是5 对重特征值与其他特征值聚集在一起,使得IRA 方法收敛的难度较大。

对Cayley 变换来说,当位移点选择合适时也可以得到系统的所有不稳定特征值。但由于事先并不能获取系统不稳定特征值的数量以及位置分布情况,需要不断改变位移点的位置,直到可以收敛到系统的全部不稳定特征值。依次选取位移点(s1,s2)为(-0.5,0.5)、 (-1,1)、 (-1.5,1.5)、 (-2,2)、 (-2.5,2.5)和(-3,3),最大重启动次数设置为50,子空间维数设置为60,收敛容差设置为10-6。当位移点(s1,s2)选择为(-2.5,2.5)和(-3,3)时,分别经过43次和40 次重启动收敛到所有的不稳定特征值。而对于其他4 组位移点,当达到最大重启动次数时,仍存在遗漏不稳定特征值的情况。

与图4 相比,在求解不稳定特征值时,指数变换在谱主导性和谱稀疏性方面都具有较大的优势。这是因为指数变换可以将所有不稳定特征值映射为主导特征值,且主导性随着特征值实部的增大而增大。当子空间维数设置为60 时,经过2 次重启动,所提双层Arnoldi 方法就可以收敛到Xing6u 系统所有的不稳定特征值。

5.2 效率测试

在本节中,利用Xing6u 和NF2016 这2 个实际系统来测试所提方法的计算效率。需要说明的是,NF2016 系统是正常运行的系统,并不包含不稳定特征值。因此,在测试过程中通过修改控制器参数使其变为不稳定系统,并包含3 对不稳定特征值,分别 为 0.447 8±j9.596 3、0.315 6±j10.081 7 和0.134 7±j13.542 2。当维数kouter设置为60、收敛容差εouter设置为10-6时,利用所提双层Arnoldi 算法,未经过重启动过程就可以收敛到全部的特征值。求解Xing6u 和NF2016 系统不稳定特征值的计算耗时如表3 所示。其中,NUnstable为不稳定特征值的个数,NIR为重启动的次数。

表3 Xing6u 和NF2016 系统的计算耗时Table 3 Calculation time of Xing6u and NF2016 systems

由表3 可知,双层Arnoldi 算法求解Xing6u 系统不稳定特征值的计算耗时为4.2 s,而QR 方法的计算耗时为13 s。对于更大规模的NF2016 系统来说,计算耗时为15.7 s。此外,由于NF2016 系统规模较大,基于本文所采用的测试环境无法用QR 方法求解全部特征值。可以看出,所提双层Arnoldi 算法可以适用于较大规模的系统。

此外,当位移点选择合适时,Cayley 变换也可以较为快速地得到系统的所有不稳定特征值。例如,当位移点选择为s1=-3 和s2=3 时,Cayley 变换求解Xing6u 系统全部不稳定特征值的耗时为1.3 s。但对任意一个系统来说,由于事先不知道不稳定特征值的分布,并不能保证一开始选取的位移点就是合适的位移点。如果用于试错的位移点数目较多,Cayley 变换的计算耗时则可能会超过所提方法。另一方面,对于大规模系统来说,所提方法的计算效率已经可以满足实际应用的需要。考虑到所采用的方法在谱主导性和谱稀疏性上具有较大的优势,其可以作为现有特征值计算方法的补充,以确保在电力系统部分特征值计算过程中能够不遗漏不稳定特征值。

6 结语

本文提出了一种基于指数变换的双层Arnoldi算法来求解大规模电力系统的不稳定特征值。该方法的主要优势在于:

1）可以将电力系统所有的不稳定特征值映射为主导特征值,并且特征值的主导性随实部的增大而增大。

2）结合指数变换的谱主导性和谱稀疏性的优势,外层Arnoldi 算法易于收敛到所有不稳定特征值,且内层Arnoldi 算法可以快速地计算其中所需的指数矩阵和向量的乘积。因此,所提方法具有较高的计算效率。

3）利用Xing6u 和NF2016 系统的数值测试表明,所提方法具有较高的计算精度。

此外,双层Arnoldi 方法是针对求解不稳定特征值提出的,而指数变换的应用使得该方法不适用于求解弱阻尼特征值。这是因为指数变换将所有的弱阻尼特征值映射为非主导特征值。考虑到位移-逆变换或者Cayley 变换在求解弱阻尼特征值时是非常高效的,可以针对不同的区域采用不同的谱变换方法。例如,在弱阻尼区域采用位移-逆变换或者Cayley 变换,而在不稳定区域采用指数变换。综上,所提方法可以作为现有特征值计算方法的补充,以确保在大规模电力系统部分特征值计算过程中能够不遗漏不稳定特征值。需要说明的是,研究更高效的指数矩阵与向量乘积计算方法对于所提方法计算效率的提升具有显著意义,这也是需进一步探索的内容。