深部岩石爆破主裂纹扩展方向与地应力的关系

葛进进，徐 颖,2，程 琳，宗 琦

(1. 安徽理工大学 土木建筑学院，安徽 淮南 232001；2. 深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232001)

随着现代化矿井开采由浅部向深部的转变，岩体赋存在高应力环境中，导致深部矿井岩石爆破破碎理论和围岩稳定机理和浅部相比发生了变化，亟待完善和丰富[1]。

有关地应力场对岩体爆破开裂及破岩效果的影响，国内外已开展不少研究[2-4]。杨仁树等[5]采用实验室模型试验，研究高应力状态下炮孔穿过层理爆破的裂纹起裂、扩展等动态力学行为；岳中文等[6]采用新型数字激光动态焦散线试验系统开展多组爆破光测试验，研究单向围压作用下切缝药包爆破爆生主裂纹的动态力学行为；杨建华等[7]采用光滑粒子流体力学-有限元方法耦合数值模拟方法，研究了高地应力作用下炮孔间裂纹的传播及贯通过程，分析了炮孔周围应力场动态演化过程与分布特征。

现有研究表明，初始地应力对爆生裂纹的发展具有明显的“抑制”作用，且爆生裂纹优先向静态应力场中最大主应力方向扩展[8]；当裂纹方向与静态压应力方向倾斜时，静态压应力场对裂纹的扩展起阻碍作用，当裂纹向静态应力场方向偏转并一致后，静态压应力场对裂纹扩展的阻碍作用大大降低[9]。根据杨立云等[10]的研究得出，这是由于初始压应力场降低了裂纹尖端的应力集中程度，阻碍了裂纹的扩展，使得爆生主裂纹的扩展距离变短，产生“抑制”作用。

在试验和生产实践中，炮孔爆破在具有动、静应力场方面的介质中表现为优先起裂，爆破效果好，炸药消耗低。张志呈等[11]称这种现象为“波导效应”。他认为，岩体内的地应力错综复杂，由于地应力的存在，岩体的动态响应也会发生变化。爆破应力波与地应力叠加有相强相弱的规律，同相位相强，反之相弱。

对此，肖正学等[12]提出“初始应力场对裂纹发展导向作用原理”。他认为，当地应力足够大，主应力方向与爆炸应力波方向一致时，爆炸应力波必然与地应力相碰并发生叠加作用，在碰撞的切向伴生拉应力，当合成拉应力值超过岩石的抗拉强度时，岩石将沿主应力方向起裂。

综上，研究者们普遍认为初始应力条件下岩石爆生径向裂纹的扩展偏向于最大主应力的方向，但是对于其作用机理却持有不同观点，尚存在争议。为此，本研究开展不同围压荷载作用下透明岩石爆破相似模型试验，研究初始应力下岩石爆破裂纹扩展的机理，揭示初始地应力对爆生裂纹扩展方向、长度和速度等的影响规律。研究结果将为深部岩体控制爆破提供理论指导，丰富深部岩石爆破理论。

1 模型试验

1.1 相似系数

根据原型和模型的平衡、几何、物理方程、应力边界条件和位移边界条件进行推导，可以得出模型试验的各物理量之间的相似关系为[13]

(1)

式中：α为相似比；L为长度；δ为位移；E为弹性模量；μ为泊松比；γ为容重;σ为应力;σc为抗压强度;σt为抗拉强度;ε为应变;X,Y,Z为体积力；C为内聚力；φ为内摩擦角；T为时间；各物理力学参数的下标p为原型，下标m为模型。

以淮南矿区丁集煤矿深部巷道为工程原型[14]，通过取芯测得原岩容重27 kN/m3、平均抗压强度为135 MPa；其断面形状类似半圆拱形，断面尺寸是5 000 mm×3 880 mm(如图1所示)考虑应力加载试验装置的有效应力加载范围以及最大荷载集度，同时为降低模型试验失真程度与尺寸效应影响程度，确定用于模拟断面的模型试件的尺寸为300 mm×300 mm×20 mm。结合原型和模型的几何尺寸，可以得出其几何相似比为αL=16.7。

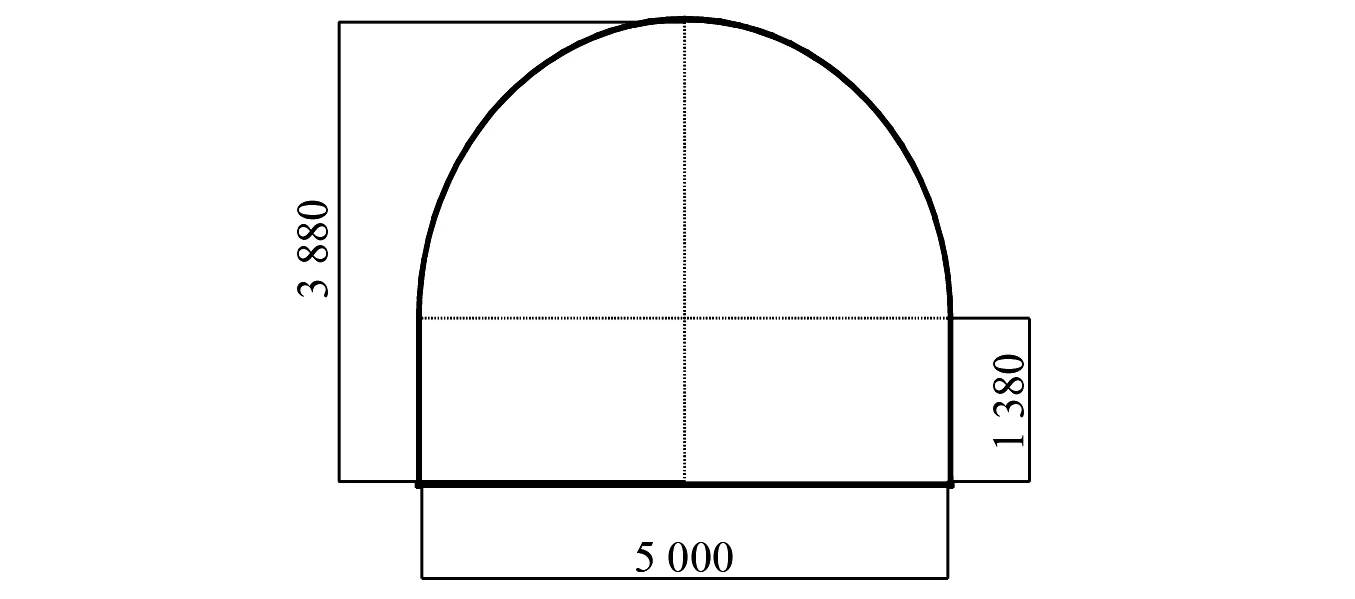
图1 巷道断面尺寸示意图(mm)Fig.1 Schematic diagram of roadway section size(mm)

第二个需要确定的就是容重相似比aγ，其与模型材料种类相关。相似模型试验使用的材料性质应尽可能地与原型相似，但目前无法得到与现场岩体条件完全一致的模型材料。所以，材料相似的条件只能近似满足。本文采用一种符合硬岩基本物理性质的透明硬岩相似材料[15]，便于爆后裂纹的观测与分析，其容重为12.3 kN/m3。再由原岩容重27 kN/m3，这样便可得到容重相似比为2.2，则相应的应力相似系数ασ=36.7。从而，理论上所需模型材料的单轴抗压强度则为3.68 MPa。

1.2 爆破动力设计

煤矿井下爆破常采用三级煤矿许用水胶炸药，其密度为1 150 kg/m3、爆速为3 600 m/s。而模型试验中所使用的炸药类型与实际爆破中的不同，因此为了遵循“炸药爆炸能量相似”原则，同时方便调整不耦合装药系数，协调炸药与模型材料的匹配性，试验采用自制小型“雷管”。该“雷管”由玻璃管、DDNP、铜丝、砂子以及橡皮泥、502胶水制作而成，其密度约为1.02 g/cm3，在玻璃管的约束下DDNP的爆速可达4 000 m/s[16]。

根据相似准则要求，相似炸药和原型炸药间应满足CρCD=1(Cρ为原型炸药与模型炸药的密度比；CD为原型炸药与模型炸药的爆速比)[17]。代入原型炸药和模型炸药参数，得CρCD=1.014，基本满足“炸药爆破能量相似”的原则。

1.3 应力加载设计

在模型材料与炸药基本符合相似准则的基础上，利用自主研制的应力加载装置提供的主动液压加载模拟模型体所处的应力环境(如图2所示)。应力加载装置模拟竖直和水平两个方向上的地应力。竖直方向σv模拟上覆岩层介质自质量，水平应力σh模拟垂直于岩石巷道轴向的水平构造应力。

图2 模型试验装置系统Fig.2 Model test equipment system

根据应力相似系数ασ=36.7，垂直应力σv=γH，设计试验模拟赋存岩体的埋深分别为0～1 600 m，则相应的竖直方向围压加载应力值与水平方向围压加载应力值为0～1.168 MPa。因此，模型试验共设计5组加载方案，如表1所示。

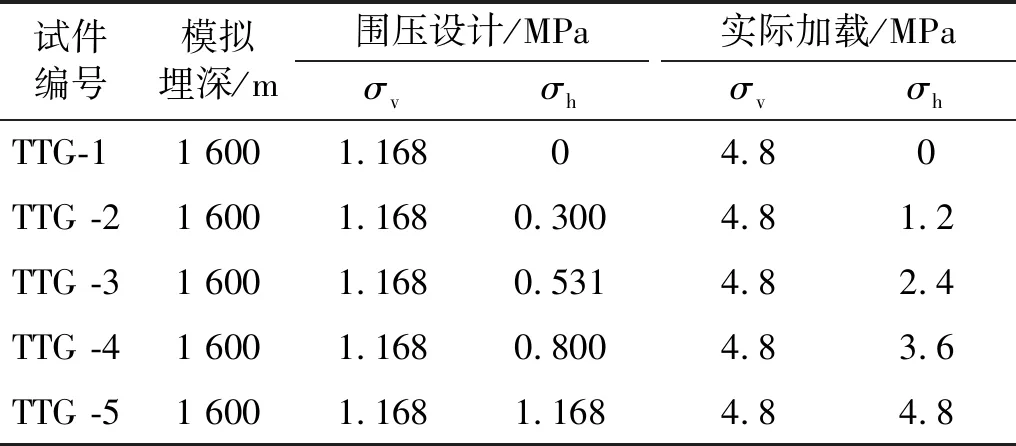
表1 模型试件应力加载方案Tab.1 Stress loading scheme of model specimen

1.4 模型参数

依据相似理论对模型材料强度、围压加载值以及炸药使用量的计算结果，进行预爆破模型试验，结果表明由于所选材料强度偏低、装药量偏大的原因，导致试件破碎程度较大，不利对爆后试件进行裂纹扩展规律的研究，因此在理论计算的基础上，结合预爆试验结果对爆破模型参数进行适当调整，实际装药以及模型试件参数如表2、表3所示。

表2 模型试件基本物理力学参数Tab.2 Basic physical and mechanical parameters of the model specimens

表3 爆破装药参数Tab.3 Blasting charge parameters

装药炮孔位于试件中心，并在其两端用2 mm厚塑料圆片黏结，用于固定特制小雷管。详细的装药结构如图3所示。

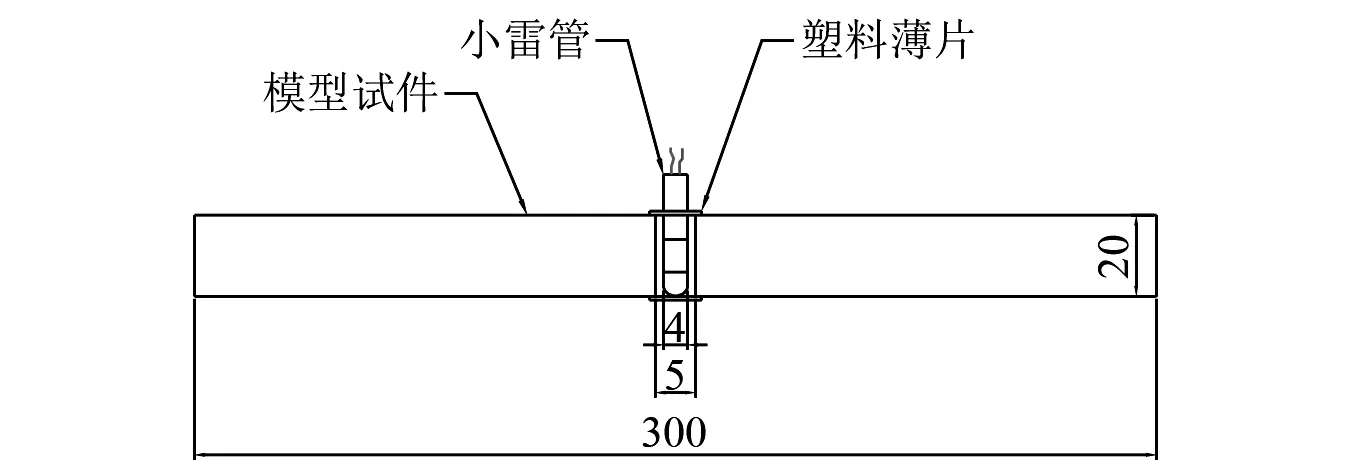
图3 装药结构示意图(mm)Fig.3 Schematic diagram for charging structure(mm)

1.5 试件制备

模型试件的尺寸规格为300 mm×300 mm×20 mm，具体制作步骤如下:

步骤1准备材料。对于环氧树脂和固化剂可以直接购得，饱和松香溶液则需要自己调配。具体做法是，将松香块打成粉末状并过100目筛子，然后将松香粉末融进适量的无水酒精溶液，直到溶液达到饱和状态时停止加入。

步骤2准备模具。爆破相似模型试验所需试件尺寸为300 mm×300 mm×20 mm，因此选择以用作导热系数测定的模具作为本次试验的模具。另据探索性试验发现，直接将混合溶液浇筑于模具内部会导致试件难以拆模，故需在浇筑前对模具进行预处理，具体做法为，先在模具表面涂一薄层凡士林，然后用防粘薄膜粘贴在其表面。

步骤3浇筑试件。首先，按照设计好的试验配比分别称取环氧树脂、固化剂，以及饱和松香溶液置于烧杯中。然后，将环氧树脂、固化剂放在50 ℃烘箱中加热，饱和松香溶液则放在50 ℃水浴锅中加热。待环氧树脂和固化剂中的气泡全部排除时，将二者混合并搅拌均匀，此时混合溶液中不可避免的再次出现气泡，仍将其置于50 ℃烘箱中继续加热直至气泡消除后拿出。最后，取出水浴锅中的饱和松香溶液倒入环氧树脂体系中，并在混合物被搅拌均匀后将其导入模具中。经过多次试验得出，只要匀速缓慢地搅拌三者混合溶液，经过预热后的饱和松香溶液与无气泡的热环氧树脂体系混合时将不再产生气泡。

2 试验结果与分析

爆后模型试件裂纹的扩展情况如图4所示。环向裂隙扩展范围(对应图中Ⅱ区)已用虚线标出；径向主裂纹(对应图中Ⅱ区、Ⅲ区)用实线标出，其中粗实线部分即为爆生主裂纹，细实线部分为主裂纹的延伸线；平行于σv方向的细实线则参考线；最长径向主裂纹与竖直方向参考线间的夹角记为φ。

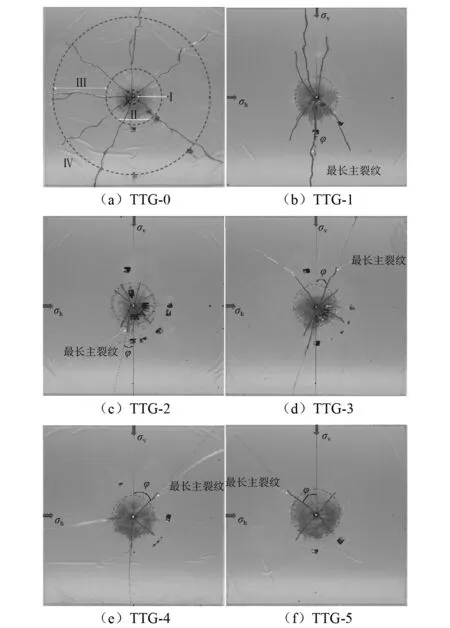
图4 爆后模型试件Fig.4 Transparent model specimens after explosion

由图4可以看出，具有初始静载作用的试件TTG-1～TTG-5爆后效果与无初始应力下试件TTG-0相比发生较大改变。采取不耦合装药的试件，其爆后效果基本符合单孔爆破的试验现象及结论[18-19]，可以划分为压碎区、裂隙区以及振动区。随着施加在试件四周应力的增加，裂隙区的范围逐渐减小，震动区的范围逐渐增大，只有压碎区的范围没有明显变化。

无初始应力时，岩石单孔爆破径向裂纹扩展呈现出由炮孔中心向四周均匀辐射的形状，显然初始应力下的爆生径向裂纹其扩展更具有“方向”性，如试件TTG-1，其最长主裂纹扩展沿着竖直应力方向。随着侧压力系数(最小主应力与最大主应力的比值)的变化，最长径向主裂纹的扩展方向与最大主应力的夹角发生变化。当侧压力系数为1时，此时最长径向主裂纹沿着试件对角线方向扩展。

另外，初始静载的施加还限制了径向主裂纹的扩展长度和数量。随着应力的增大，径向主裂纹的扩展长度逐渐减小，并趋于环向裂隙圈的直径大小。由图4可以很明显的看到，试件TTG-1上有6条径向主裂纹，而试件TTG-5上只有4条径向主裂纹。

为定量分析径向主裂纹扩展方向与主应力的关系、径向主裂纹扩展长度与侧压力系数的关系，基于爆后模型试件的裂纹扩展情况进行重构，如图5所示。

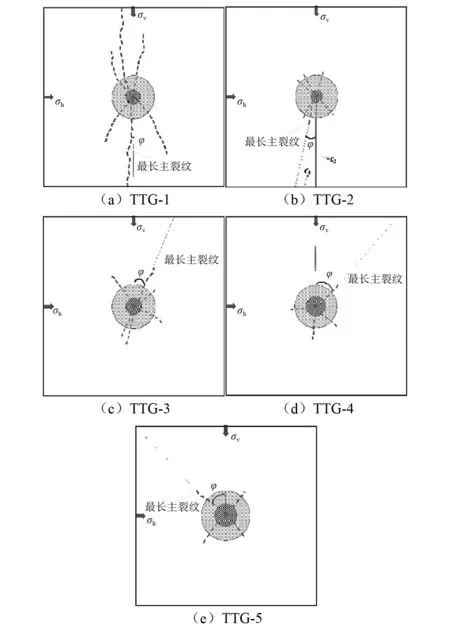
图5 爆后模型试件裂纹扩展形态Fig.5 Crack propagation of model specimens after explosion

2.1 最长主裂纹扩展方向与最大主应力的关系

从图5(a)中可以看出，TTG-1试件的主裂纹扩展沿着σv方向，这与单向荷载约束下爆破模型试验的裂纹扩展规律相同。图5(e)则显示出TTG-5试件爆破主裂纹扩展沿着斜45°，这与双向等荷载约束下爆破模型试验的裂纹扩展规律相同[20]。而图5(b)和图5(c)则显示出TTG-2～TTG-4试件与前述试验结论有所不同，裂纹的扩展与最大主应力(σv)的方向呈锐角，且该锐角的大小随着最小主应力(σh)的增大而增大。

记最长径向主裂纹与竖直应力方向的夹角为φ；最长主裂纹的延长线与试件边缘的交点到试件边长中点的距离(交点与中点间的距离)记为C1；炮孔中心到模型试件边缘的垂直距离记为C2，且沿着σv方向，如图5(b)所示。那么，tanφ的值可以通过计算C1与C2的比值得到。根据对各爆后模型试件C1与C2的测量值，可计算得到tanφ值如表4所示。

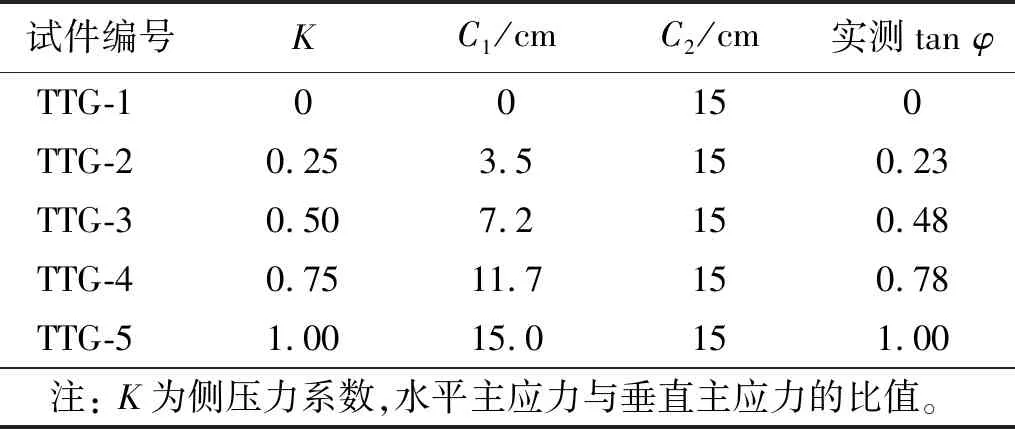
表4 tan φ实测值Tab.4 Measured value of tan φ

从表4可以看出，随着侧压力系数的变化，实测tanφ也在发生变化，且二者之间的数值大小极为接近，尤其是当K=0和K=1时，与tanφ的值相等，这意味着侧压力系数与最长径向主裂纹扩展方向之间必然存在联系。为探究初始静载对最长径向主裂纹扩展方向的影响机制，本文将在第3章讨论部分做深入分析。

2.2 主裂纹扩展长度与侧压力系数的关系

图5显示径向主裂纹的数量和长度均受侧压力系数的大小影响，即随着模型试件TTG-1～TTG-5上侧压力系数的增大，其径向主裂纹的数量和长度均在减小。为定量表征模型试件中径向主裂纹长度随着侧压力系数的变化的规律，选取5个模型试件中的部分径向裂纹统计于表5中。

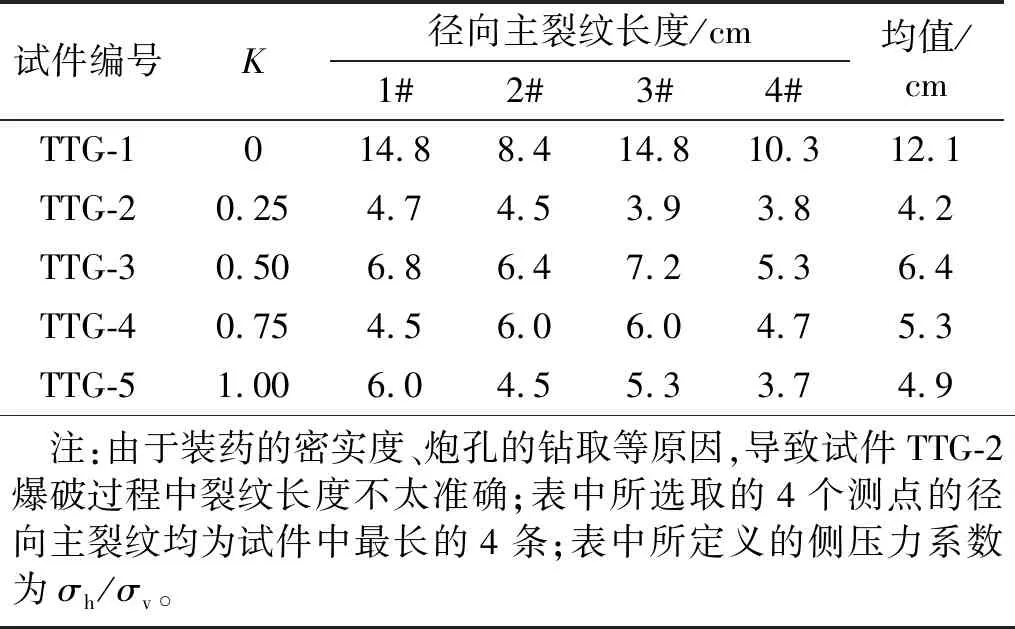
表5 模型试件中的径向主裂纹长度Tab.5 Radial main crack length in the model specimens

从表5中可以看到，最长和平均径向主裂纹的长度均随着侧压力系数的增加而逐渐减小(TTG-2试件除外)。进一步，以侧压力系数为横坐标，最长和平均径向主裂纹的长度为纵坐标可以绘出图6。

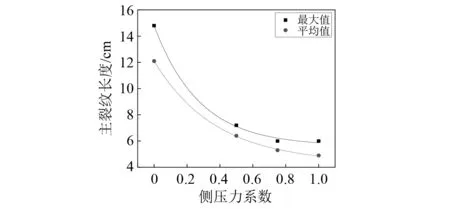
图6 主裂纹长度随侧压力系数的变化规律Fig.6 Length for main cracks varies with lateral pressure coefficient

图6清晰反映了径向主裂纹的扩展长度随侧压力系数的变化规律，对其数据进行拟合还可以得到，最长径向主裂纹的扩展长度与侧压力系数符合下列关系式

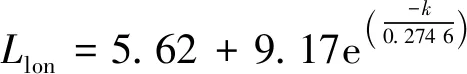
(R2=0.998 6,k∈(0,1))

(2)

而平均径向主裂纹的扩展长度与侧压力系数之间的关系为

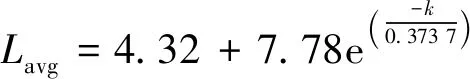
(R2=0.999 8,k∈(0,1))

(3)

式中：k为侧压力系数，为σh与σv的比值；Llon为最长径向主裂纹扩展的长度；Lavg为径向主裂纹扩展的平均长度。式(2)、式(3)反映出双向不等围压荷载下的径向主裂纹扩展情况主要依赖于侧压力系数的变化。

由上述关系式可知，当代入实际侧压力系数的大小时，可计算得出岩石爆生径向最长主裂纹的长度以及径向主裂纹长度的平均值。但本文模型试验并未严格遵循相似准则，因而由模型试验得到的结果不能直接用于原型试验，在实际深部岩体爆破中进行爆破参数设计时，需要结合现场测试数据对由式(2)、式(3)的计算值进行修正。

3 讨 论

裂隙区是工程爆破中岩石破坏的主要部分，其破坏的范围比压缩粉碎区大得多。根据裂隙区裂纹的形态，又可以分为环向裂隙和径向裂隙。而对于裂隙区径向主裂纹的扩展，则主要由爆破应力波所衍生的环向拉伸应力导致。试验结果表明，初始应力对压缩粉碎区的影响相对较小，而对裂隙区裂纹扩展影响较大，尤为明显是最长径向主裂纹的扩展，因此本节借助爆炸力学、弹性力学以及爆破应力波等理论尝试解释初始应力下最长径向主裂纹沿最大主应力方向扩展的机理。

基于深部岩体所受应力状态[21-22]，采用动静组合的加载方式来模拟爆破动载和地应力的作用(见图7)；鉴于本文所涉及均为平面爆破模型试验，实际炮孔封堵效果较差，因而不考虑爆生气体对模型试件的致裂作用。设在竖直方向上岩体所受的初始应力为σy；在水平方向上所受的初始应力为σx；内部所受的爆炸荷载为Pd；岩石的抗压强度为σc，抗拉强度为σt。

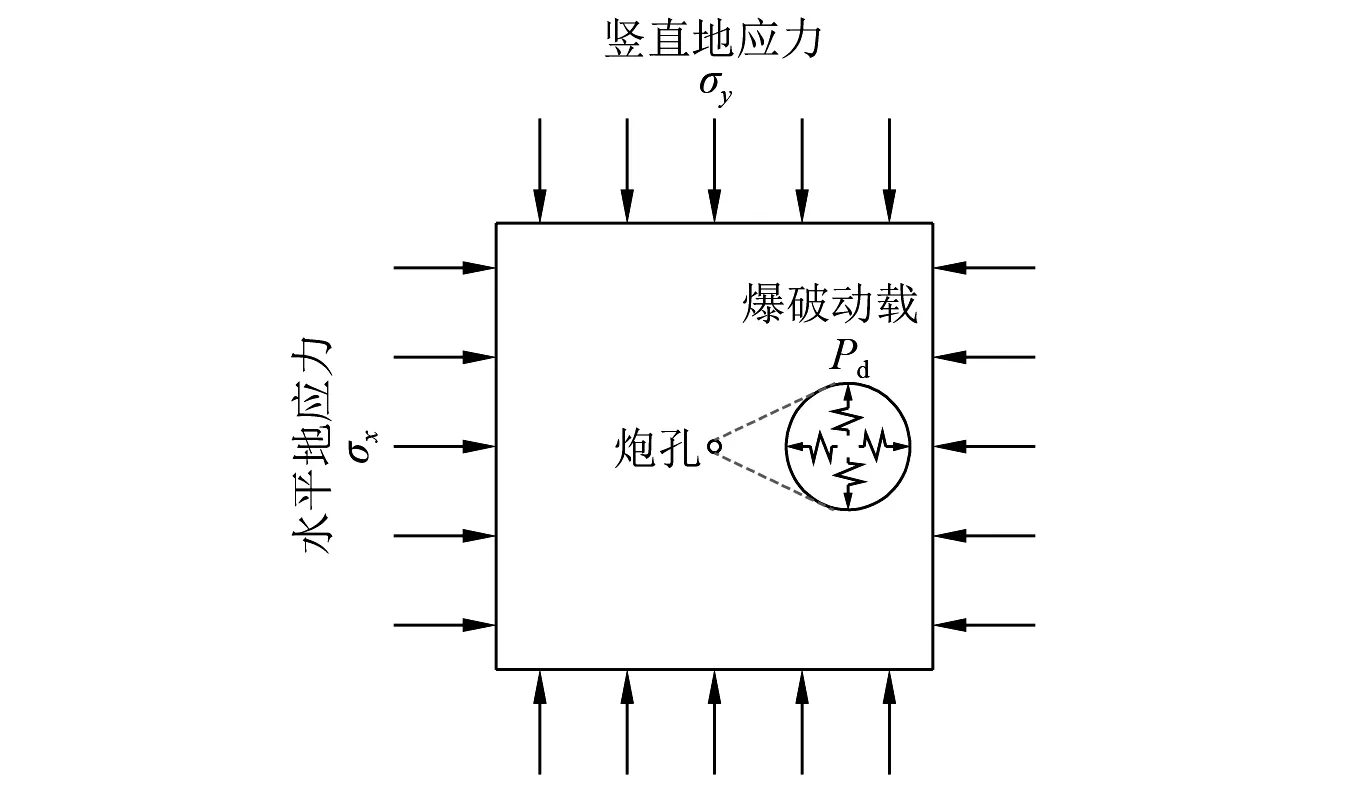
图7 深部岩体爆破受力模型Fig.7 Force model of deep rock mass under blasting

当处于静地应力状态的岩石受到炸药爆炸的动态加载时，会在某一时刻开始发生破坏，此过程中地应力对岩石的作用通常被视为准静态加载。根据现有爆破理论，当由爆破应力波衍生的环向拉应力大于岩石的抗拉强度时，岩石便产生径向裂纹。

3.1 σx=0, σy>0

即当水平方向无初始应力时，假设模型所受的地应力状态为：σx=0,σy>0，此时受力模型可以简化为如图8(a)所示，并且将爆炸荷载记为P1，P2(P1=P2)。

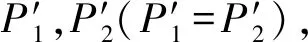
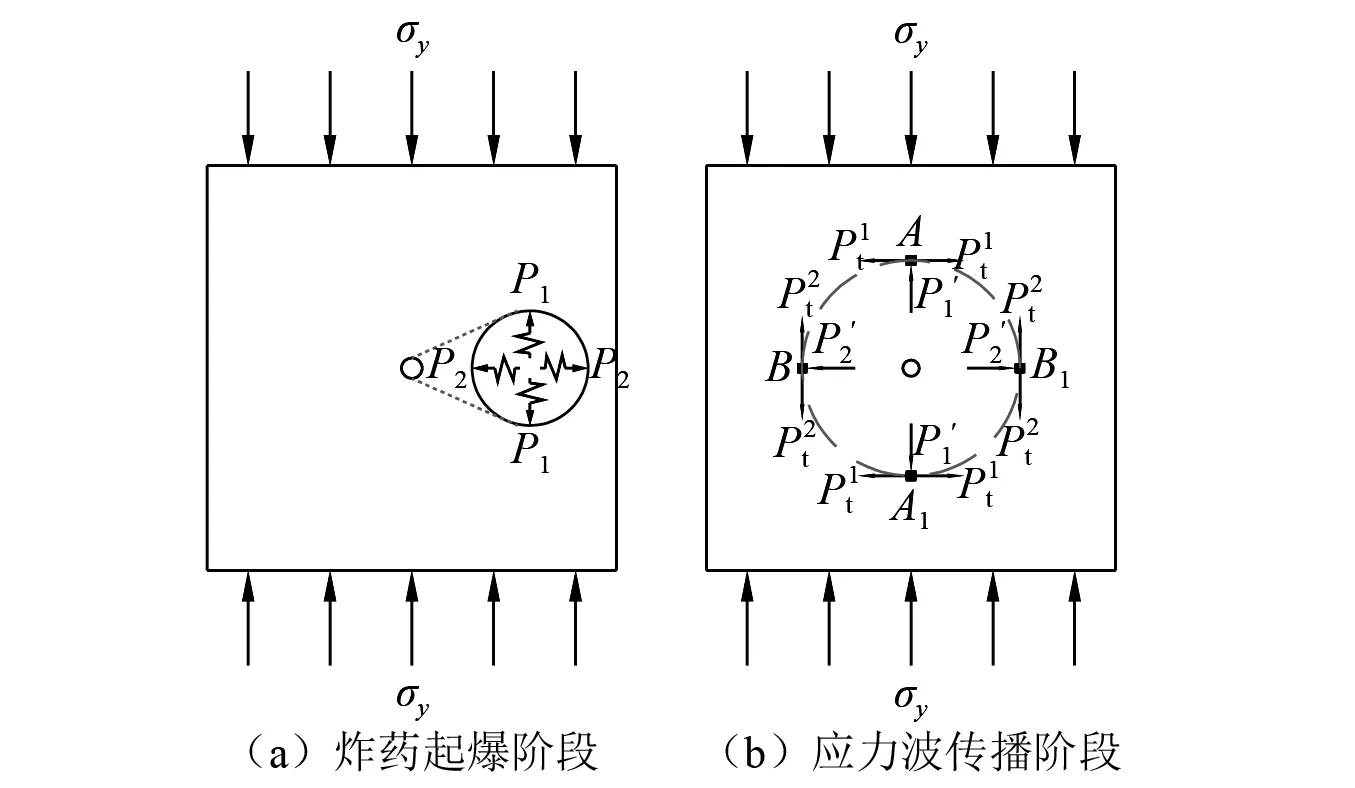
图8 单向初始应力条件下岩体爆破受力模型Fig.8 Force model of rock mass under unidirectional initial stress and blasting

为便于分析初始静载和爆破应力波对模型作用的力学机理，进一步将单向初始应力条件下岩体爆破受力模型等效为图9的力学模型(外荷载作用模型+内荷载作用模型)。

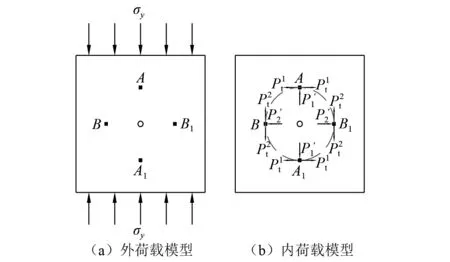
图9 单向初始应力条件下岩体爆破等效受力模型Fig.9 Equivalent force model of rock blasting under a bidirectional initial stress

戴俊等[23]认为，初始静载对岩体的作用，实则间接增加了岩石的动态抗压或者抗拉强度，基于此观点，本研究首先通过静力平衡分析，计算出外荷载作用下模型内部各微元所受初始静载的作用大小，从而便于比较各微元的抗压或抗拉强度的变化。假设模型的边长为a，由应力与荷载的关系可以将模型简化为如图10所示。图10中：σya为集中荷载；M为平移集中荷载后所产生的附加弯矩，大小为σyad，其中d为平移距离。需要说明的是，本文所添加的模型应力均远小于岩石抗压强度。由平移集中荷载会所增加的附加弯矩，虽然对得岩体内部产生剪应力，但是也远不足以对岩体产生破坏作用，故在此不考虑附加弯矩对岩体内部带来的剪切作用。

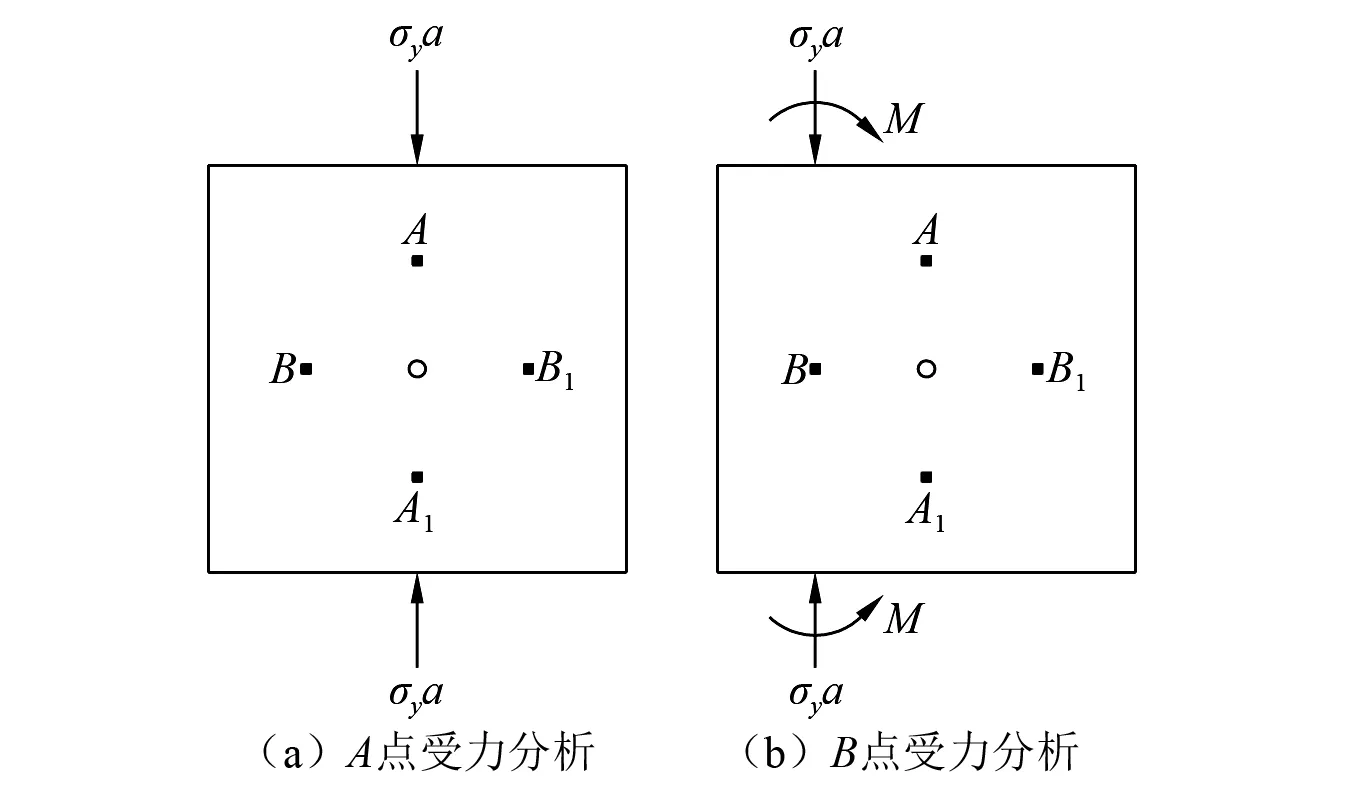
图10 初始静载作用下岩体微单元点的受力分析Fig.10 Force analysis of a micro element point in a rock mass under an initial static load

显然图9(a)所示受力状态为对称结构，故可以将上述4个受力点按照A，A1和B，B1两部分进行受力分析。根据图10(a)可以得到，微元点A，A1在竖直方向受外荷载作用，其大小为σya；根据图10(b)可以得到，微元点B，B1在竖直方向受外荷载作用，其大小为σya。假设微元点在竖直方向受到集中荷载(σya)压缩作用时，其该方向上拉伸强度增强100%，那么模型试件在沿该方向的抗拉强度变为2σt。

现有的爆破理论已经指出，在爆破中区，爆破应力波已经不足以能够压碎岩体，因此爆破应力波在A，A1点的竖直方向更不可能产生任何压缩破坏，对于A，A1点只需要讨论水平方向的拉伸应力破坏。同样，在B，B1点的水平方向不可能产生任何压缩破坏，对于B，B1点只需要讨论竖直方向的拉伸应力破坏。根据图9(b)可以得到爆破荷载作用下微元点A、点B的受力分析，如图11所示。

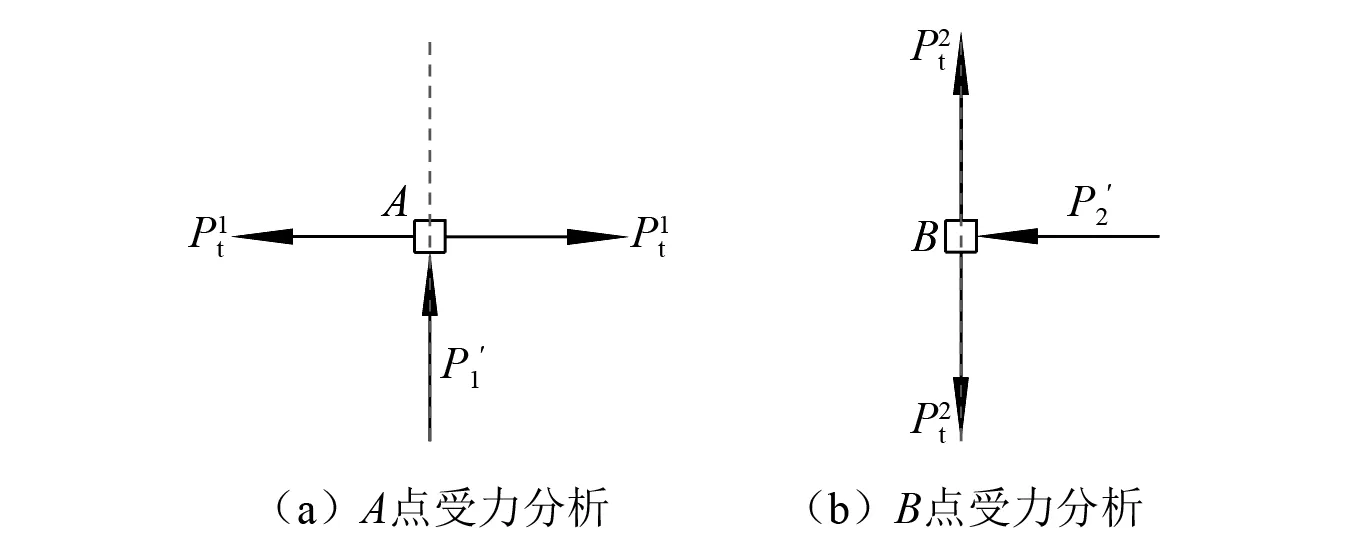
图11 爆破荷载作用下岩体中微元点的受力分析Fig.11 Force analysis of micro element points in rock mass under a dynamic blasting load

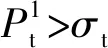
3.2 σx=σy≠0

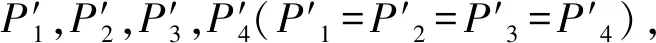
进一步将双向初始应力条件下岩体爆破受力模型等效为图13的力学模型(外荷载作用模型+内荷载作用模型)。

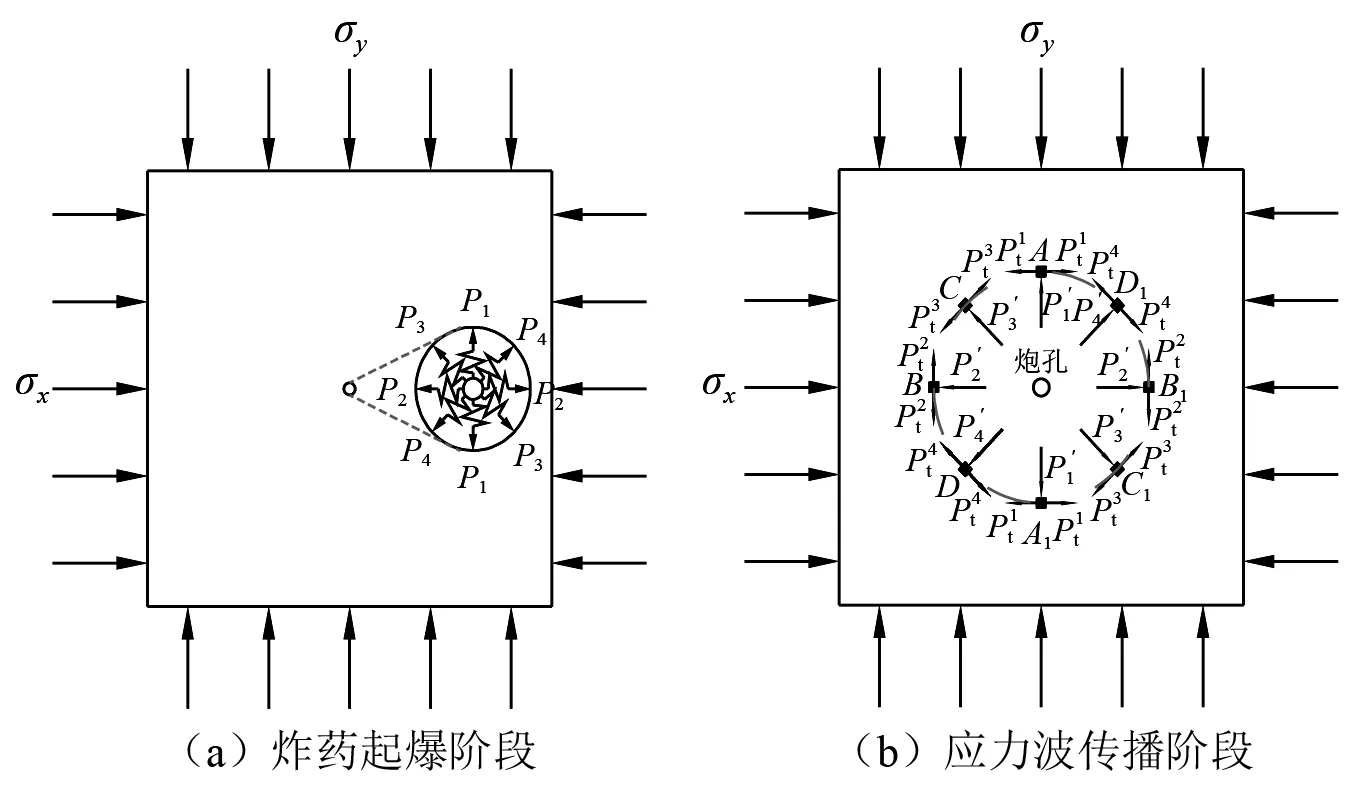
图12 双向等围压荷载下岩体爆破受力模型Fig.12 Force model of rock mass under bidirectional equal confining pressure and explosive load

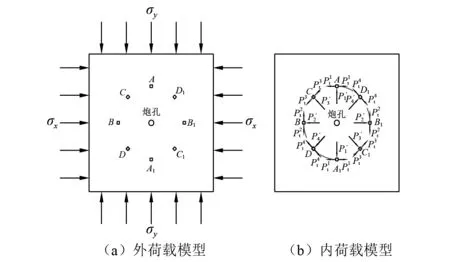
图13 双向初始应力条件下岩体爆破等效受力模型Fig.13 Equivalent force model of rock blasting under a bidirectional initial stress

根据图13(a)，本研究首先通过静力平衡分析，计算出模型内部各微元所受初始外静载的作用大小，从而得出各微元的抗压或抗拉强度的变化。由图13(a)所示模型的对称性，取其一半进行分析，如图14所示。

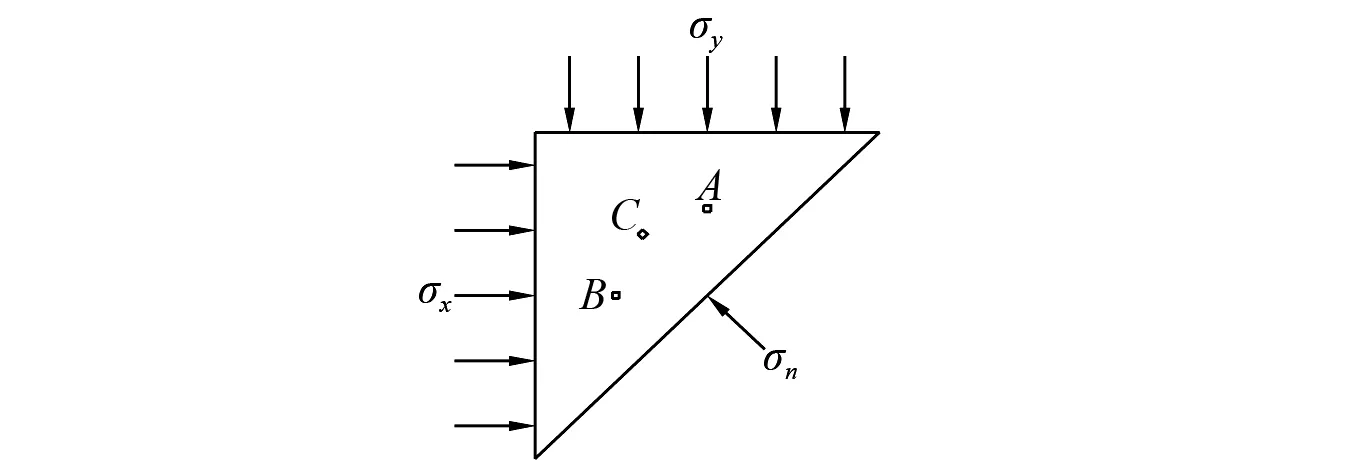
图14 图13(a)的半个受力模型Fig.14 Half of the force model in figure 13(a)

假设模型的边长为a，由应力与荷载的关系可以将模型简化为图15(a)。由σx=σy，可假设σx=σy=σ，这样可以根据平移分别得到微元点A，B，C受集中荷载作用如图15(b)～图15(d)所示。同样，在此不考虑附加弯矩对岩体内部带来的剪切作用。

根据图15(b)可以得到，微元点A在水平、竖直方向均受外荷载作用，其大小为σa；根据图15(c)可以得到，微元点B在水平、竖直方向均受外荷载作用，其大小为σa；根据图15(d)可以得到，微元点C在水平、竖直方向均受外荷载作用，其大小为σa，并且可计算出其沿着斜向(即与竖直方向夹角45 ℃的方向)受到外荷载作用的大小为0.707σa。假设微元点在竖直方向受到集中荷载(σa)压缩作用时，其该方向上拉伸强度增强100%，那么模型试件在沿该方向的抗拉强度变为2σt。

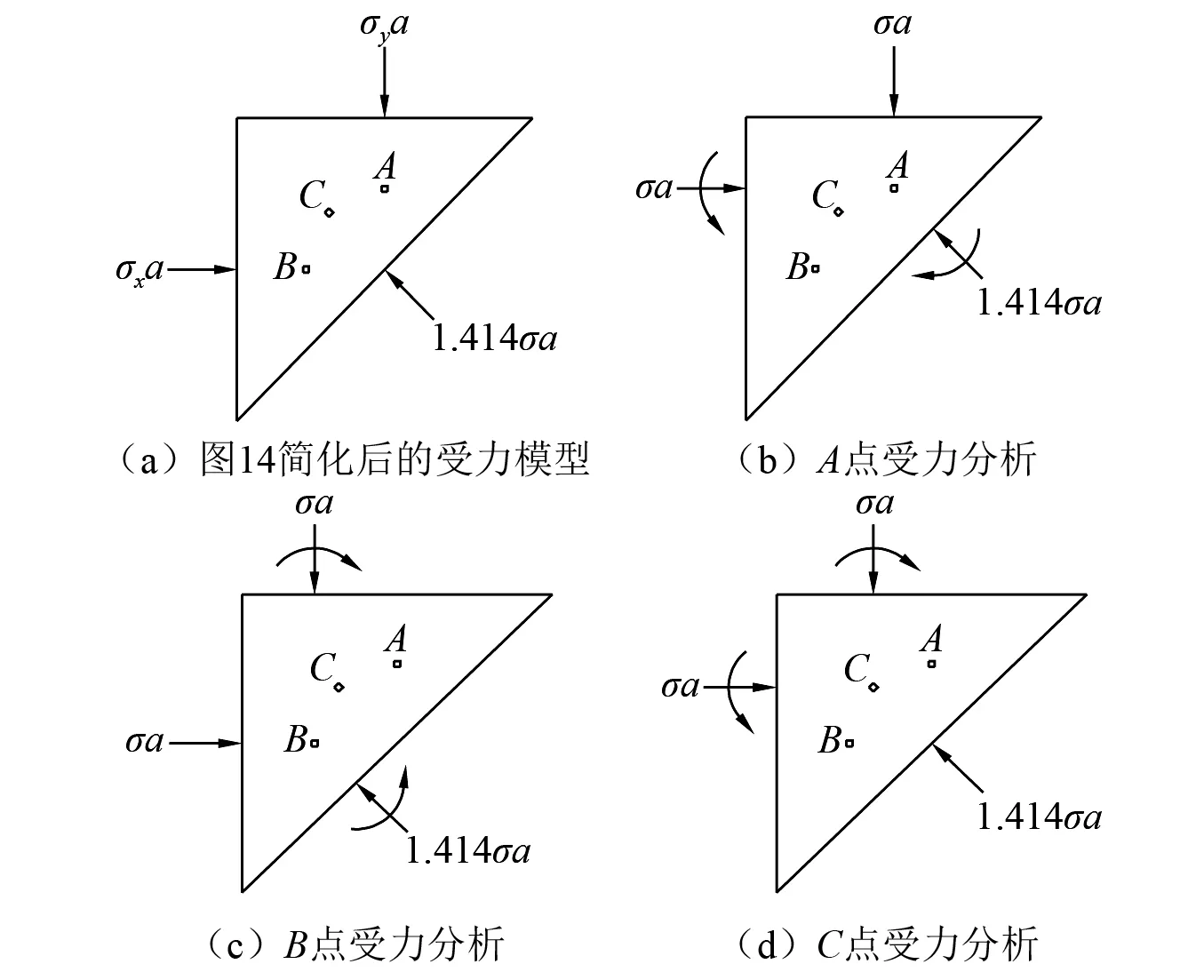
图15 初始静载作用下岩体微元点的受力分析Fig.15 Force analysis of a micro element point in a rock mass under an initial static load

根据图13(b)，取微元点A，B，C进行为分析，可以得到图16。

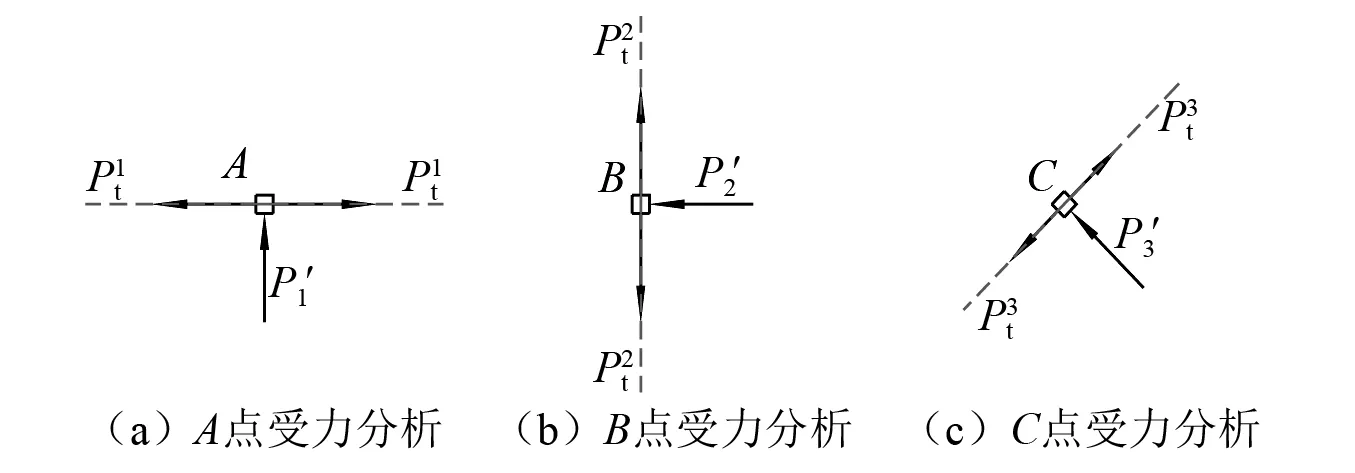
图16 爆破荷载作用下岩体微元点受力分析Fig.16 Force analysis of micro element points in rock mass under a dynamic blasting load

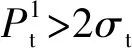
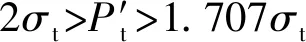
从而可得出沿着AA1/BB1方向的裂纹必然先于沿着CC1/DD1方向裂纹而停止发展，换言之，AA1/BB1方向裂纹的总长度小于CC1/DD1方向裂纹的总长，宏观上表现为径向裂纹沿着斜45 ℃方向发展。

3.3 σx≠σy≠0

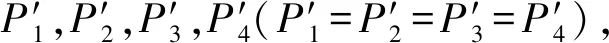
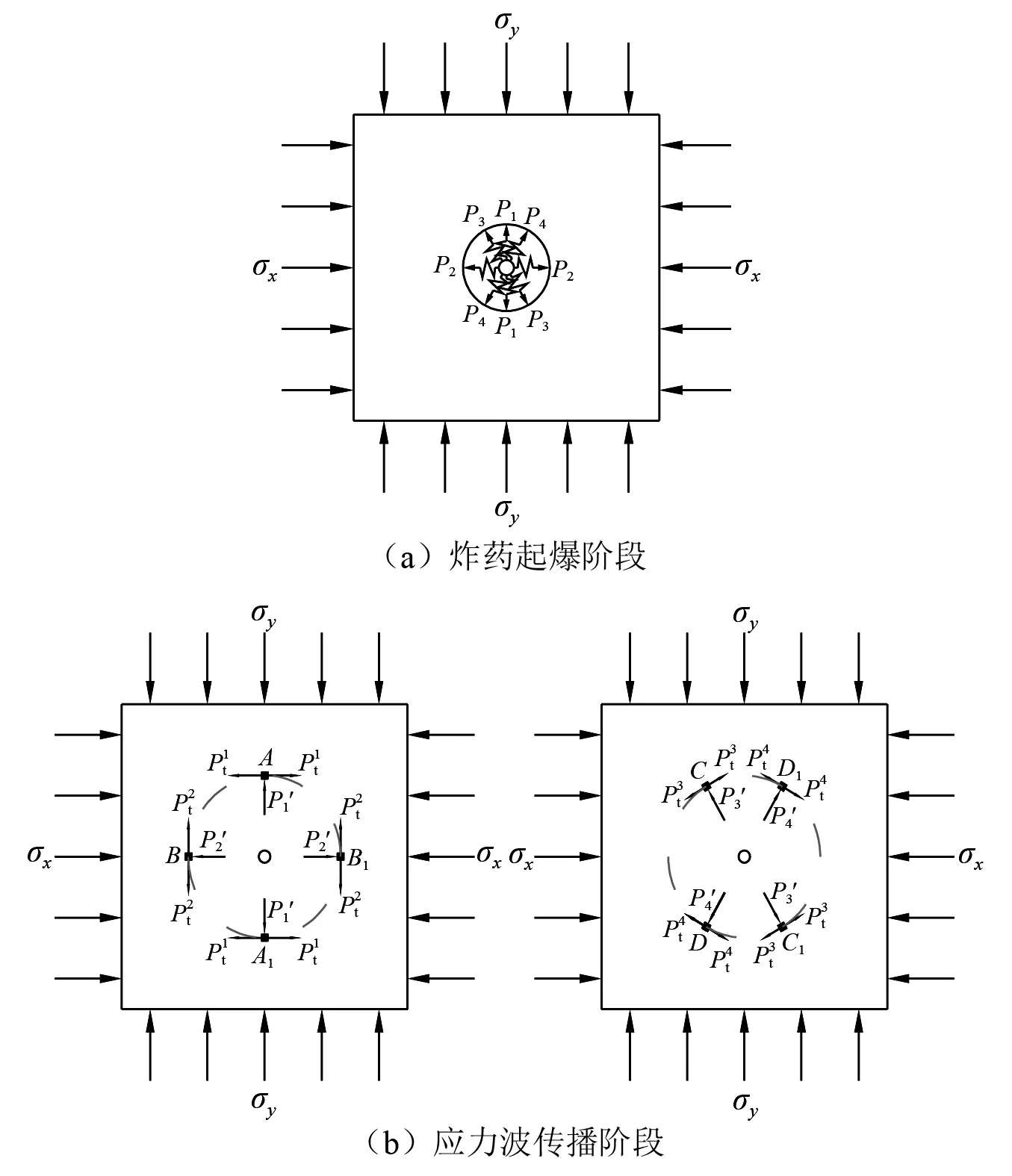
图17 双向不等围压荷载下岩体爆破受力模型Fig.17 Force model of rock mass under bidirectional unequal confining pressure and explosive load

进一步将双向初始应力条件下岩体爆破受力模型(见图17(b))等效为图18的力学模型(外荷载作用模型+内荷载作用模型)。

本研究首先通过对图18(a)所示的模型进行静力平衡分析，计算出模型内部各微元所受初始外静载的作用大小，从而得出各微元的抗压或抗拉强度的变化。根据图18(a)所示模型的对称性，取其一半进行分析，如图19(a)所示。假设模型的边长为a，2σx=σy=2σ，由应力与荷载的关系可以将模型简化为图19(b)和图19(c)。进一步将斜截面上的法向应力和剪应力合并，并根据平移分别得到微元点A，B，C受集中荷载作用如图19(d)～图19(f)所示。同样，在此不考虑附加弯矩对岩体内部带来的剪切作用。

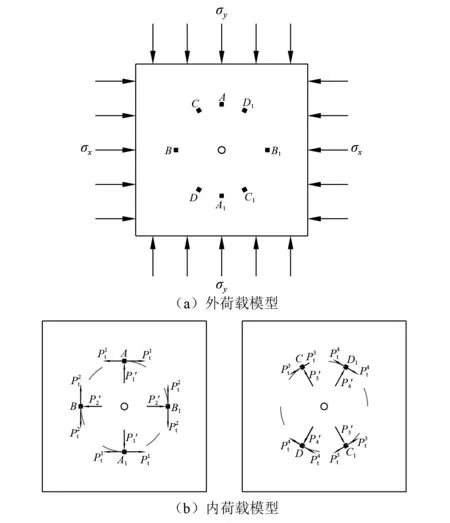
图18 双向初始应力条件下岩体爆破等效受力模型Fig.18 Equivalent force model of rock blasting under a bidirectional initial stress

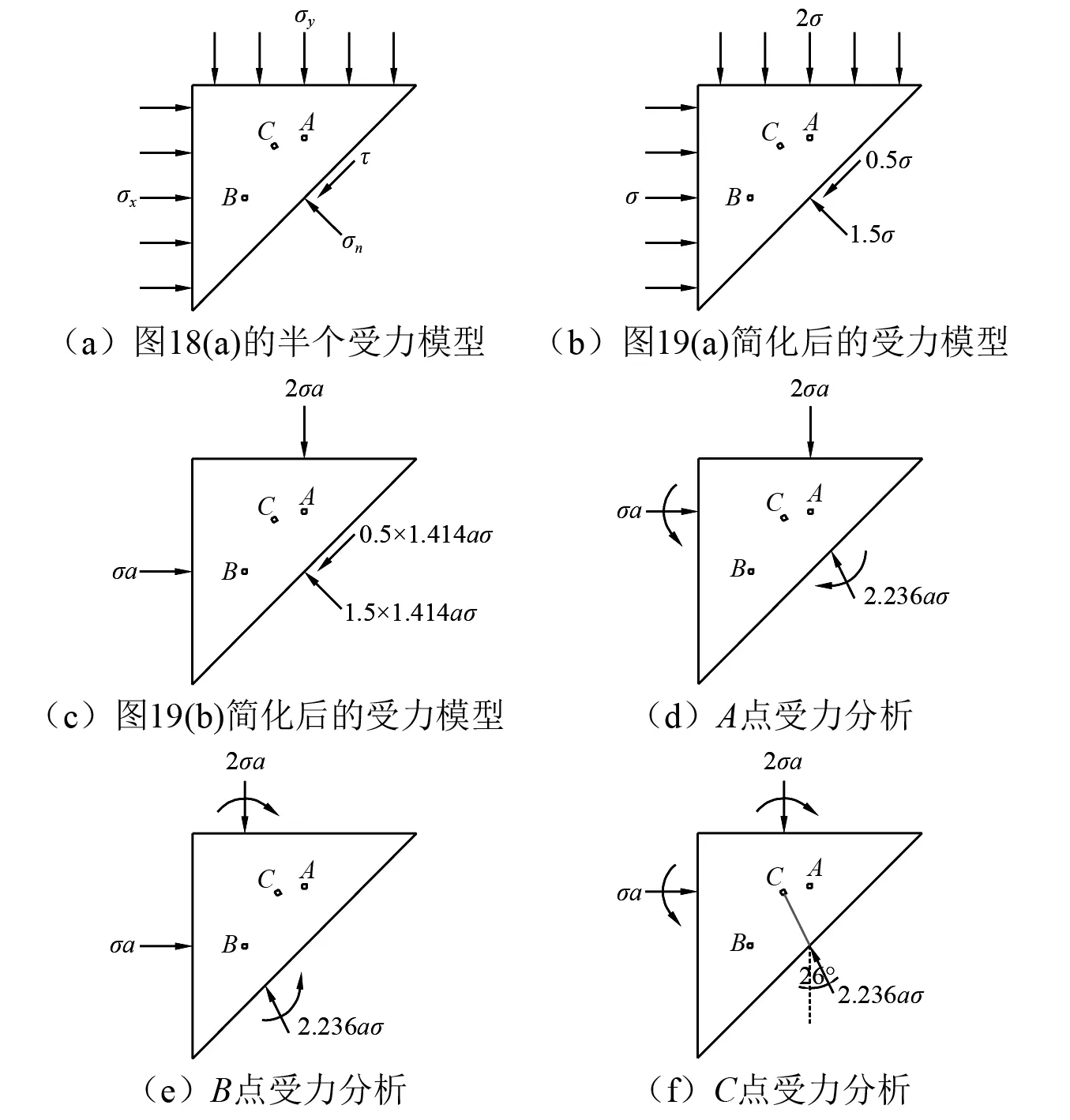
图19 初始静载作用下岩体微元点的受力分析Fig.19 Force analysis of a micro element point in a rock mass under an initial static load

根据图19(d)可以得到，微元点A在水平、竖直方向均受外荷载作用，其大小分别为σa，2σa；根据图19(e)可以得到，微元点B在水平、竖直方向均受外荷载作用，其大小分别为σa，2σa；根据图19(f)可以得到，微元点C在水平、竖直方向均受外荷载作用，其大小分别为σa，2σa，这里需要注明的是：本研究中假设微元点C与斜边中点的连线(CO)与合力的延长线平行，并且可计算出其沿着炮孔切向(即与CO垂直的方向，与竖直应力方向夹角64°)受外荷载作用的大小为0.894σa。假设微元点在竖直方向受到集中荷载(σa)压缩作用时，其该方向上拉伸强度增强100%，那么模型试件在沿该方向的抗拉强度变为2σt。

根据图18(b)，取微元点A，B，C进行为分析，可以得到图20。

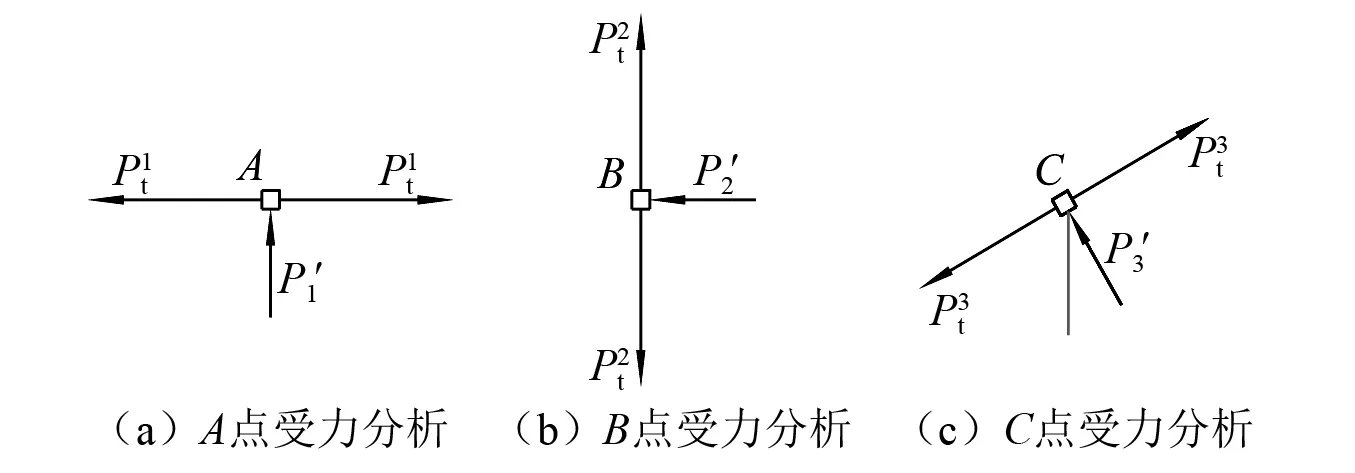
图20 爆破荷载作用下岩体微元点受力分析Fig.20 Force analysis of micro element points in rock mass under a dynamic blasting load

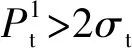
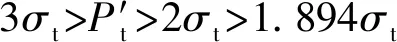
因此，可以得出沿着AA1/BB1方向的裂纹必然先于沿着CC1/DD1方向裂纹而停止发展，而沿着BB1方向的裂纹又会先于沿着AA1方向裂纹而停止发展，换言之，BB1方向裂纹的总长度小于AA1方向裂纹的总长，而AA1方向裂纹的总长度小于CC1/DD1方向裂纹的总长，宏观上表现为最长径向裂纹靠近最大主应力方向发展。

据此可以得到，最长主裂纹扩展方向CC1/DD1与竖直方向的夹角φ的大小为26°，而tanφ的值近似等于水平方向主应力与竖直方向主应力的比值(σ/2σ)，可表示为tanφ=σx/σy。结合3.1节和3.2节所得结果，可将此计算式推广到0～45 ℃的范围内(0≤tanφ≤1)，并借助第2章模型试验结果对其进行检验。当σx=0，σy≠0，tanφ=0，φ=0°时，与模型试件TTG-1结果吻合；当σx=σy≠0，tanφ=1，φ=45°时，与模型试件TTG-5结果吻合；当σx≠σy≠0时，根据理论计算结果与2.1节模型试验测量结果极为接近，可以认为tanφ的理论计算值与实际测量值是一致的。

从而可以得到

(4)

这里σx可以等于0，但是σy不能为0，且σx≤σy即σy作为最大主应力方向，且不等于0。

这样，只要知道最大主应力和最小主应力的大小和方向，就可以确定最长主裂纹的扩展方向。

4 结 论

本研究针对当前深部岩体爆破中存在的初始地应力具有“导向作用”问题，开展围压荷载作用下透明岩石爆破相似模型试验，并结合理论分析与模型试验的结果得到双向不等荷载条件下爆破裂纹扩展规律：

(1) 初始应力下，径向主裂纹的数量和长度均受侧压力系数的大小影响，即随着模型试件上侧压力系数的增大，其径向主裂纹的数量和长度均在减小。另外，随着侧压力系数的变化，最长径向主裂纹的扩展方向与最大主应力的夹角也发生变化。

(2) 单向围压荷载条件下，模型试件上最长主裂纹沿着竖直方向扩展；双向等围压荷载条件下，模型试件上最长主裂纹沿着对角线方向扩展。

(3) 双向不等荷载条件下，模型试件上的爆生最长径向主裂纹扩展的方向与最大主应力的方向呈锐角，且该锐角的大小随着最小主应力的增大而增大,同时可以根据tanφ=σx/σy确定φ值得大小。

本研究成果可以对初始应力条件下岩石爆生最长主裂纹扩展方向进行预测，从而可以正确利用初始应力场以减少资源损失、节约能源、改善爆破效果等，这对深部岩体工程的爆破具有重要的参考价值。需要指明的是，由于本文研究结果是基于均质岩体的假设而得出，即利用均质透明相似材料模拟天然岩石，未能考虑天然岩石的非连续性、各向异性等诸多因素，同时理论分析中还对深部岩石爆破的力学模型做了大量的简化和假定，这均会导致其研究结果的一些局限性。因此，在后续的研究中，不仅需要考虑主要影响因素还要考虑次要影响因素，从而进一步丰富深部岩体爆破破岩机理。