带非对称阻尼器的柔性支撑框架主余震作用分析
2023-02-27袁苗苗卢文胜
谷 子,樊 圆,袁苗苗,卢文胜
(同济大学 土木工程学院 结构防灾减灾工程系,上海 200092)
柔性支撑结构是由柔性支撑(tension-only brace,TOB)作为主要抗侧力构件的结构。TOB是一种只能承受拉力而不能承受压力的支撑形式,如图1所示。由于其不承受压力,所以设计过程中柔性支撑截面尺寸只需要考虑满足抗拉强度设计要求,而不需要考虑因长细比不足导致的支撑受压整体失稳问题。相比于传统的双向支撑(如图2所示)和消能减震支撑(如图3所示),TOB具有以下特点:①造价低廉且易于布置,不影响建筑美观;②机理清晰,只存在平面内力学特性;③节约空间,适合结构加固工程;④可采用焊接或机械连接,易于施工。

图1 柔性支撑Fig.1 Tension-only brace

图2 双向支撑Fig.2 Bi-directional brace

图3 消能减震支撑Fig.3 Energy dissipative brace
将柔性支撑运用于装配式钢结构、可恢复功能结构以及既有结构加固改造中,已经得到国内外众多学者的关注。新型分层装配式钢结构工业化建筑体系[1]采用TOB作为主要的抗侧力构件,陈越时等[2-3]以某采用TOB的3层足尺钢框架结构为研究对象进行了振动台试验研究,结果表明,采用柔性支撑的低层结构具有良好的抗震性能和震后可恢复性能。Cortés-Puentes等[4]使用形状记忆合金材质TOB加固混凝土剪力墙,提高了构件的强度和自复位能力。Lago等[5]将TOB用于提升未进行抗震设计老旧单层厂房的抗震性能。
TOB可由扁钢制成,存在拉伸松弛和压缩松弛两方面问题,影响其性能发挥。扁钢TOB的拉伸松弛问题即扁钢TOB受拉屈服后塑性拉伸Δl,结构复位后扁钢TOB松弛,并在之后加载中形成长度为Δl的不能为结构提供刚度的“零刚度区间”,也会在地震过程中产生有害冲击作用[6]。如图4所示:TOB-1在加载过程中的弹性阶段为结构提供了刚度并产生塑性,但在卸载过程中没有刚度;扁钢TOB的压缩松弛问题即TOB在受压时屈曲,完全拉紧前不工作;TOB-2在加、卸载过程中均不参与工作,不起任何支撑和耗能作用。
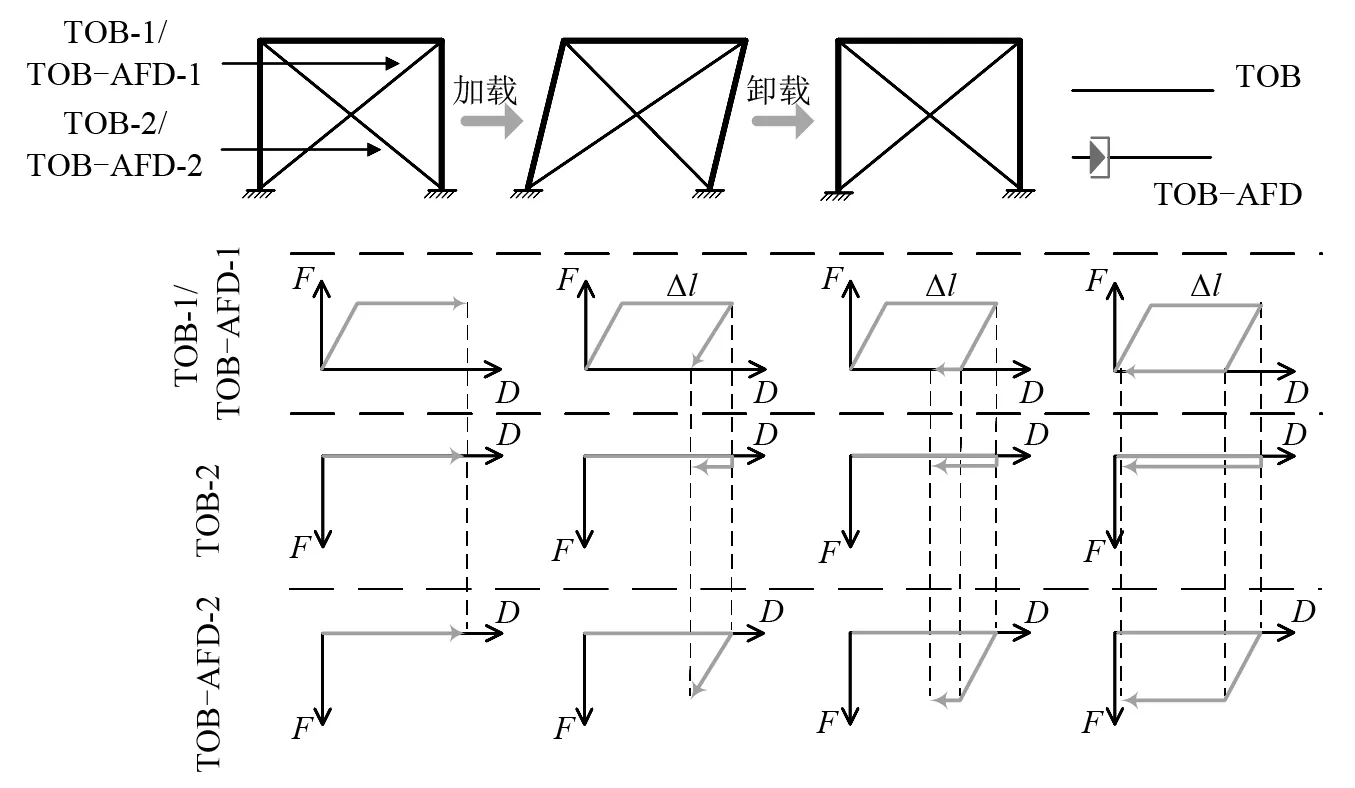
图4 TOB/AFD框架加、卸载支撑滞回曲线Fig.4 Hysteretic curves of frames with TOB/AFD under loading and unloading
扁钢TOB的松弛和结构体系性能退化相叠加,导致柔性支撑结构在主余震耦合作用中可能严重破坏。扁钢TOB作为耗能构件[7],塑性拉伸松弛性能下降并逐渐退出工作导致结构体系性能退化,相同外部激励下结构响应逐渐变大,又进一步增大了扁钢TOB“零刚度区间”。所以,结构很可能在主震峰值地面加速度时刻结构的响应不是最剧烈的,主震造成的损伤导致余震阶段产生更为剧烈的破坏,即主余震的耦合作用导致结构破坏。以往研究认为TOB在一般地震结束后可人工修复,恢复结构的抗震性能水平,而在实际主余震之间很难做到及时修复[8]。
一些研究者提出使用附加的装置消除屈曲和屈曲造成的影响,提升TOB的弹塑性往复工作性能。Mousavi等[9]开发了TOB免松弛装置,使TOB在压缩过程中可以自由滑入端部设备,解决两类松弛造成的不利影响。但是这类设备受限于传动杆的长度和卡齿的数量,工作行程有限,主余震地震动反复激励下累积行程很可能超过工作行程,造成免松弛设备失效。
综上,目前缺乏解决TOB在主余震耦合作用下两类松弛问题的解决方法。因此,本文开发了一种具有非对称弹塑性模型特征的非对称摩擦阻尼器(asymmetrical friction damper,AFD)。AFD与TOB串联形成TOB-AFD并对称布置在框架结构中,工作性能见图4,TOB-AFD有效解决了TOB的两类松弛问题。图4中,AFD的符号与阻尼器符号相似,但因其非对称力学特性,故将传统阻尼器符号的平头改为三角形表示。第5章的非线性时程分析证实AFD在小震下逐渐“自拉紧”,与同参数TOB相比提供更大的恢复力;在中震、大震主余震耦合下保证柔性支撑结构性能不下降,并摩擦耗能,为结构提供附加阻尼,提高结构的抗震性能。
1 非对称摩擦阻尼器的性能简述
AFD如图5所示,AFD通过机械棘轮原理,受拉时棘轮传动带动主、副摩擦板与摩擦片间发生摩擦。而当装置承受压力时,棘轮只空转不传动,摩擦板和摩擦片之间不发生摩擦。于是AFD实现在受拉方向上产生摩擦阻尼力而在受压方向上几乎不产生阻尼力,与TOB受拉工作而受压不工作一致。AFD在摩擦板与摩擦片相对静止时提供静摩擦力,相对滑动时提供滑动摩擦力。

注:1.金属外壳;2.传动杆;3.包含棘轮的齿轮组;4.主摩擦板;5.副摩擦板;6.摩擦片;7.预紧力螺栓。图5 AFD的3D模型Fig.5 3D drawing of AFD
由于棘轮传动的转动特性,AFD的工作性能不受累积行程影响,在地震过程中不退化。更多关于AFD及其齿、棘轮的设计及工作细节可参见文献[10]。根据上述原理加工制造的非对称阻尼器模型,如图6所示。

图6 AFD模型实物Fig.6 Physical sample of AFD
AFD的试验装置如图7所示,其左端与被考虑为固定端支座的反力架相连;右端通过力传感器与作动器相连。力传感器可以准确地测量并记录作动器施加给AFD的作用力。试验采用了4组最大量程为±50 mm 的拉线式位移计测量传动杆与金属外壳的相对位移,即为AFD的工作位移。针对不同预紧力Fp和最大工作位移dmax共进行12组试验。Fp为30 kN,dmax为±28 mm的典型滞回曲线如图8所示。

图7 AFD试验装置Fig.7 Test setup of AFD

图8 AFD典型工况与理论模型对比Fig.8 Comparison between typical AFD testing case and theoretical model
AFD的理论模型可用式(1)~式(3)进行表示
Δd=d-dturn
(1)
(2)
(3)
式中:d为以初始位置为0点的AFD运动位移变量;dturn为AFD由受拉转变为受压或从受压转变为受拉时刻的位移值;Fmax,Fmin分别为AFD受拉、受压阻尼力。理论模型与试验结果的对比参见图8。通过比较可发现,AFD的本构特征可以很好地被理论模型模拟,具有稳定的非对称弹塑性特征。
2 非对称弹塑性特征理论模型分析
2.1 弹性或静摩擦阶段理论模型及性能演化
文献[11]认为,结构的支撑应在小震下保持弹性工作,对应双向支撑或消能减震支撑、扁钢TOB的弹性工作阶段和TOB-AFD的静摩擦工作阶段。
根据式(1)~式(3),可推导TOB-AFD在静摩擦工作阶段(Δd≤dke)的理论模型,如图9所示。

图9 TOB-AFD静摩擦工作阶段理论模型Fig.9 Theoretical model of TOB-AFD in static friction phase
弹性工作阶段双向支撑或消能减震支撑符合线弹性模型,如图10(a)所示,力随位移呈线性增长或下降。扁钢TOB遵循Gap模型,如图10(b)所示,受拉过程中保持线弹性,受压屈曲几乎不提供恢复力。对称布置的扁钢TOB压缩松弛,在弹性阶段可以提供与双向支撑或消能减震支撑相同的工作性能。
TOB-AFD的工作性能十分特殊,在静摩擦工作阶段具有显著的非线性“自拉紧”特征。根据图9模型绘制的TOB-AFD工作模型图,如图10(c)所示。由图10可知:①1-2,恢复力从0随被拉伸线性增加;②2-3,荷载反向后恢复力线性卸载;③3-4,受压以Fmin≈0恒值力运动;④4-5,荷载反向由受压转为受拉,由受压位移最大值4为起始点拉伸,恢复力由Fmin随位移增加线性增长;⑤5-8,同②~④过程。此外,TOB-AFD的恢复力随位移非线性增长,随历史最大位移的增大而增大;与压缩松弛的扁钢TOB相比具有非线性“自拉紧”特征。
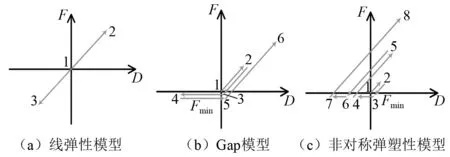
图10 弹性或静摩擦阶理论模型及性能演化Fig.10 Theoretical models and performance evolving in elastic or static friction phase
对比图10(a)、图10(b)、图10(c)可发现,由于非线性“自拉紧”特征,TOB-AFD在静摩擦阶段以与双向支撑或消能减震支撑、扁钢TOB相同的位移,提供更大的恢复力,使结构响应更小。
2.2 弹塑性阶段或滑动摩擦阶段理论模型及设计方法
双向支撑或消能减震支撑理论模型,如图11(a)所示。然而,在实际使用过程中消能减震支撑却在一些条件下以小于设计荷载和非设计破坏模式发生失效[12-14],同时也由于非约束区域出现塑性铰、临近构件产生脆性断裂和平面外效应造成了理论模型不准确。
扁钢TOB本构如图11(b)所示,同时具有压缩松弛和拉伸松弛问题。对称布置的扁钢TOB作为耗能构件,塑性拉伸产生“零刚度区间”与结构体系性能退化耦合,并逐渐增大。当“零刚度区间”扩大到一定范围,扁钢TOB完全失去对结构的支撑和阻尼耗能能力,导致柔性支撑结构转化为一个无支撑结构。对于主余震地震动下这样的现象极为明显,可能产生倒塌风险。
TOB-AFD本构如图11(c)所示。对称布置的TOB-AFD拥有饱满的滞回环,不存在两类松弛问题,性能不退化,稳定耗散能量,可用式(1)~式(3)进行表示。

图11 弹塑性或动摩擦阶段理论模型Fig.11 Theoretical models after yielding or sliding
Chopra[15]证明库伦摩擦力在阻尼比较低时可以用黏滞阻尼进行等效。由于Fmin非常小可以忽略不计,所以在一个具有振幅u的振动循环中,单个TOB-AFD摩擦所耗散的能量Wc为
Wc=2Fmax·u
(4)
GB 50011—2010《建筑抗震设计规范》[16]对结构附加阻尼比ζa的计算公式为
(5)
式中:Wcj为第j个设计滑动摩擦力为Fmax j的TOB-AFD在一周往复循环耗散的能量;Δuj为第j个TOB-AFD两端的相对水平位移;θj为第j个TOB-AFD的消能方向与水平面的夹角。
(6)
GB 50011—2010《建筑抗震设计规范》对不考虑扭转效应时,第i个位移为ui的质点在水平地震作用下总应变能给出的公式为
(7)
式中,Fi为第i质点水平地震作用标准值。将式(6)、式(7)代入式(5),得到含有j组对称布置、参数不同的TOB-AFD对包含i个平动自由度结构附加的阻尼比为
(8)
2.3 拉紧保护模式和阻尼耗能模式
根据TOB-AFD在静摩擦阶段非线性“自拉紧”特征和滑动摩擦阶段的耗能特征,可以分别开发出有效保护柔性支撑的拉紧保护模式和阻尼耗能模式。
拉紧保护模式充分依靠TOB-AFD的非线性“自拉紧”特征,在工作的绝大多数时间内保持静摩擦,不耗能。其中TOB在任何时候不松弛,保证结构体系性能不下降。此方案对TOB-AFD的工作性能有一定要求。
阻尼耗能模式使用TOB-AFD在相同位置与TOB并联,AFD的参数数值远小于TOB数值。AFD持续耗能为体系提供附加阻尼,减小结构响应,从而减小TOB的拉伸松弛。
3 主余震地震动的模拟
3.1 主震地震动的选取
主震地震动根据DGJ 08-9—2013《建筑抗震设计规程》[17]选取2条人工地震动和5条天然地震动,如表1所示。表1中,持时为地震动不包含事前及事后记录的时长。7条地震动的平均谱与规范谱对比如图12所示。

表1 地震动记录Tab.1 Ground motion records
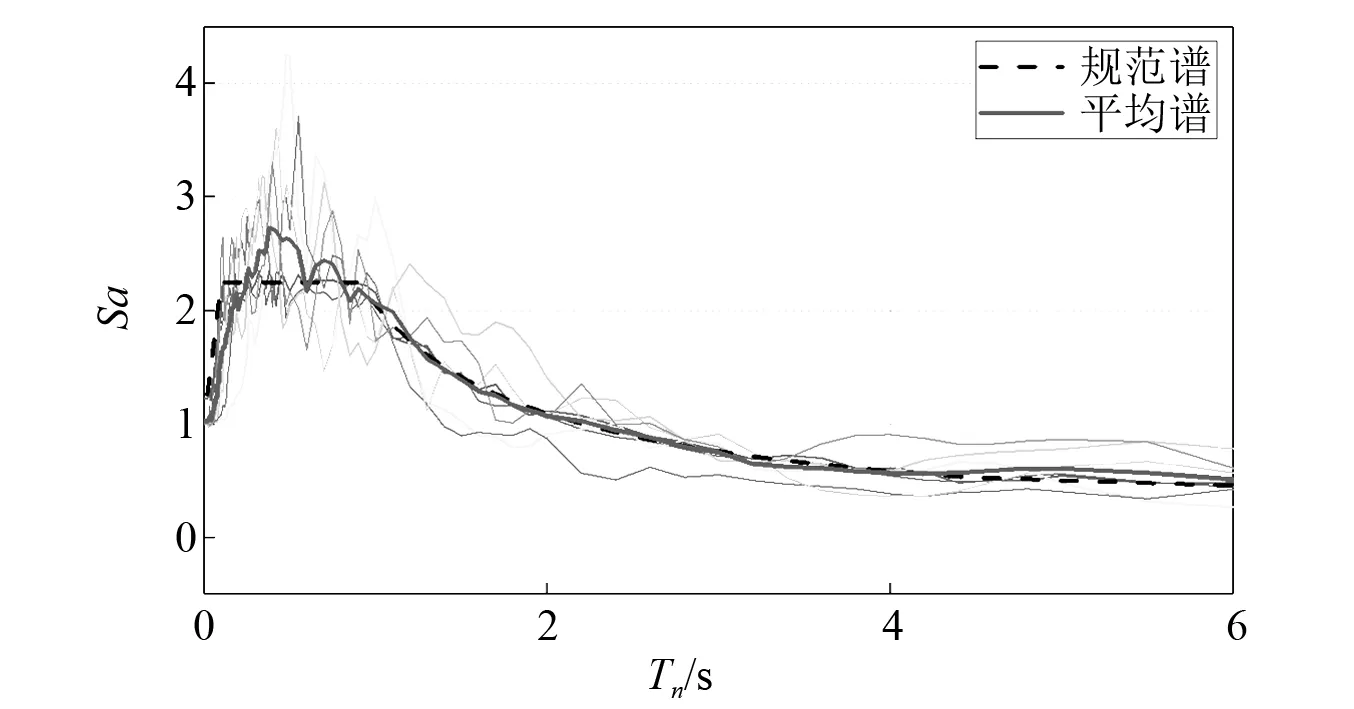
图12 地震动反应谱Fig.12 Response spectrum of the ground motions
3.2 主余震地震动的模拟
主余震地震动的模拟可挑选真实主余震地震动序列[18],也可以采用人工模拟方法构造[19]。本文采取人工模拟方法构造主余震型地震动。
在实际地震过程中,余震通常是在主震作用下产生结构振动静止后再次作用在结构上的。薛云勤[20]认为主余震之间时间间隔的长短对结构反应没有明显影响。温卫平等[21]对主余震地震动间施加了30 s的时间间隔,并发现30 s的时间足够4层、8层、12层框架结构在余震地震动作用之前停止振动。梁岩等[22]的研究同样证明时间间隔取30 s有效,并使用Joyner-Boore经验公式计算得主震峰值地面加速度×0.852 6后可以表示余震峰值地面加速度。温卫平等统计了50条主余震地震动中,主震峰值地面加速度和余震峰值地面加速度的关系,发现主震峰值地面加速度略低于余震峰值地面加速度且拟合出的关系与梁岩等的计算结果十分接近。
取用梁岩等的方法对7条主震地震动处理得到主余震地震动。在主震后施加30 s时间间隔,之后将余震调幅为主震的0.852 6倍并衔接在其后,典型的主余震地震动时程如图13所示。
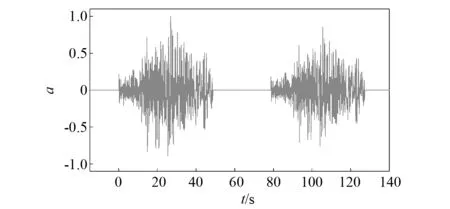
图13 由5号地震动产生的主余震地震动时程Fig.13 Mainshock-aftershock time history of ground motion No.5
4 柔性支撑结构模型介绍
选用一个3层钢框架柔性支撑结构作为数值分析模拟对象,检验扁钢TOB和TOB-AFD的拉紧保护模式和阻尼耗能模式对结构减震性能的影响。框架按照GB 50017—2017《钢结构设计标准》[23]设计,一致使用Q345号钢材,每层层高为3.3 m且平面布置相同,每层使用的截面梁柱构件尺寸如图14所示。图14中灰色部分在分析模型中分别取:
TOB方案——采取刚度为k,屈服力为Fy的扁钢TOB;
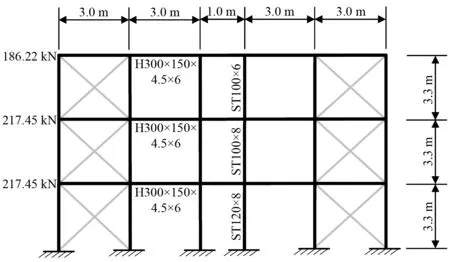
图14 分析模型Fig.14 Analysis model
拉紧方案——采用拉紧保护模式,其刚度ke和阻尼力Fmax与扁钢TOB刚度k和屈服力Fy相同的TOB-AFD;
阻尼方案——采用阻尼耗能模式,混合使用TOB和TOB-AFD。由TOB提供TOB方案k和Fy的90%;由TOB-AFD提供TOB方案k和Fy的10%的ke和Fy。
3种方案分析模型框架部分参数均相同,支撑参数如表2所示。

表2 支撑参数Tab.2 Braces parameters
使用有限元分析软件OpenSees[24]建立分析模型。分析模型的梁、柱分别使用OpenSees中的displacement-based beam-column element进行模拟,同时考虑柱的P-Δ效应。模型使用Steel 01材料模拟钢材非线性行为,并根据GB 50017—2017《钢结构设计标准》选取参数。结构的质量凝聚在模型节点上,阻尼比取为3%[25-26]。
5 主余震耦合作用下的非线性时程分析
针对柔性支撑结构模型开展非线性时程分析,比较它们对结构性能的影响。GB 50011—2010《建筑抗震设计规范》和DGJ 08-9—2013《建筑抗震设计规程》规定多高层钢结构小震下弹性层间位移角限值为1/250,弹塑性限值为1/50。
5.1 小震作用分析
小震下主震引起的结构响应很小,主余震分析相应结果不大于主震。时程分析结果如图15和表3所示。TOB方案中TOB处在弹性工作阶段,而拉紧方案中AFD未产生滑动摩擦,阻尼方案中TOB保持弹性,而AFD开始耗能。3种支撑形式最大层间位移角均小于DGJ 08-9—2013《建筑抗震设计规程》和梁岩等研究中对弹性层间位移角要求的1/250。结合图15和表 3可以发现,由于TOB-AFD的非线性“自拉紧”特征,在刚度相同的条件下,拉紧方案以一半的层间位移角提供了大于TOB方案的弹性恢复力。而TOB-AFD的耗能使阻尼方案的层间位移角同样小于拉紧方案。这说明拉紧保护模式和阻尼耗能模式均能够有效减小层间位移角。

图15 3号地震动主震1层3种支撑滞回曲线(小震)Fig.15 Hysteretic curves under frequently occurred earthquake, at story 1, GM No.3

表3 各层层间位移角与支撑轴力(小震)Tab.3 Interstory drift ratios and brace forces of each story (Frequent earthquakes)
5.2 中震下主余震耦合分析
中震下3种支撑均能够有效抑制结构产生过大的层间位移角,为结构提供刚度和阻尼。
中震下TOB方案中TOB屈服发生拉伸松弛,结构性能劣化。由表4可知,在余震PGA小于主震的情况下,相比于主震单独作用,主余震工况下TOB方案结构层间位移角平均值增大了5.8%。由图16(a)中2个明显的滞回环形状可以明确看出,TOB主震下在这2个循环内集中耗散能量并伴随着“零刚度区间”长度的显著增长,造成了结构体系性能的迅速下降。图16(b)中最右侧的狭窄滞回环表明主余震作用下,余震PGA虽然小于主震,但由于TOB的两类松弛问题,余震产生的结构响应大于主震。阻尼方案在主震下持续滑动摩擦耗能,但结构体系的抗震性能并未下降。由式(8)求得中震下平均附加阻尼比为4.38%。如图16(c)所示,主余震作用下相比主震滞回环增加部分在主震最大滞回环的包络线以内,说明阻尼方案在余震作用中仍然可以有效消耗结构能量,不使结构性能劣化。

表4 各层层间位移角与支撑轴力(中震)Tab.4 Interstory drift ratios and brace forces of each story (Design basis earthquakes)

图16 5号地震动主震1层3种支撑滞回曲线(中震)Fig.16 Hysteretic curves of the three kinds of braces on first story under ground motion No.5 (Design basis earthquakes)
由表4中拉紧保护方案和阻尼保护方案主余震与主震差异为0可知,中震下拉紧方案和阻尼方案均可以改善结构性能,使结构在余震作用下破坏情况不超过主震,且2种方案中支撑的轴力均小于TOB方案,验证了拉紧保护模式和阻尼耗能模式的有效性。
5.3 大震下主余震耦合分析
在大震主震单独作用下,3种支撑弹塑性时程分析验算最大平均层间位移角为1/89,1/310,1/216,各层均满足DGJ 08-9—2013《建筑抗震设计规程》对弹塑性层间位移角要求的1/50。
图17和表5表明:TOB方案中全部TOB均到达屈服力值,塑性耗能;拉紧方案中只有3层支撑在部分工况下未达到滑动摩擦条件;阻尼方案中TOB-AFD摩擦耗能,除部分3层TOB外其他TOB略微出现屈服。
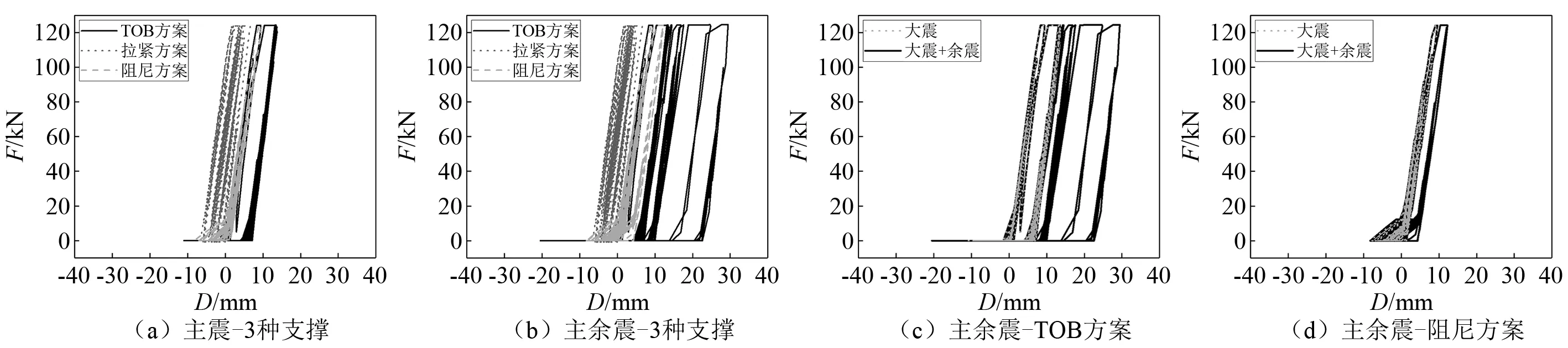
图17 2号地震动主震1层3种支撑滞回曲线(大震)Fig.17 Hysteretic curves of the three kinds of braces on first story under ground motion No.2 (Rare earthquakes)

表5 各层层间位移角与支撑轴力(大震)Tab.5 Interstory drift ratios and brace forces of each story (Rare earthquakes)
表5和表6描述了3种分析结构及其支撑在主余震作用下的性能。TOB方案中结构响应发生了剧烈变化。表5中,TOB方案数值空缺是由于其分析模型在4条主余震地震动作用下倒塌。表6补充了TOB方案分析模型在主震、主余震下的层间位移角对比。选取倒塌的2号地震动绘制图17,主震使TOB方案产生松弛,结构的整体刚度下降,原结构TOB方案以弹性势能储存地震能量的能力消失,结构无法耗散的能量转化为TOB的塑性变形并逐步松弛,同时导致结构层间位移角逐步增大,结构在P-Δ效应作用下发生倒塌。这表明扁钢柔性支撑松弛与柔性支撑结构性能下降的耦合关系是柔性支撑结构主余震耦合现象的本质原因。主震造成的严重松弛,导致在余震过程中结构直接倒塌。由表5可知, 拉紧方案由静摩擦转向滑动摩擦开始耗能层间位移角变化幅度为1.3%,可忽略不计。而阻尼方案的层间位移角变化幅度为9.6%。图17(d)中主余震作用下阻尼方案的滞回环在主震滞回环外包络线外部有所增加,阻尼方案的TOB出现了部分拉伸松弛。
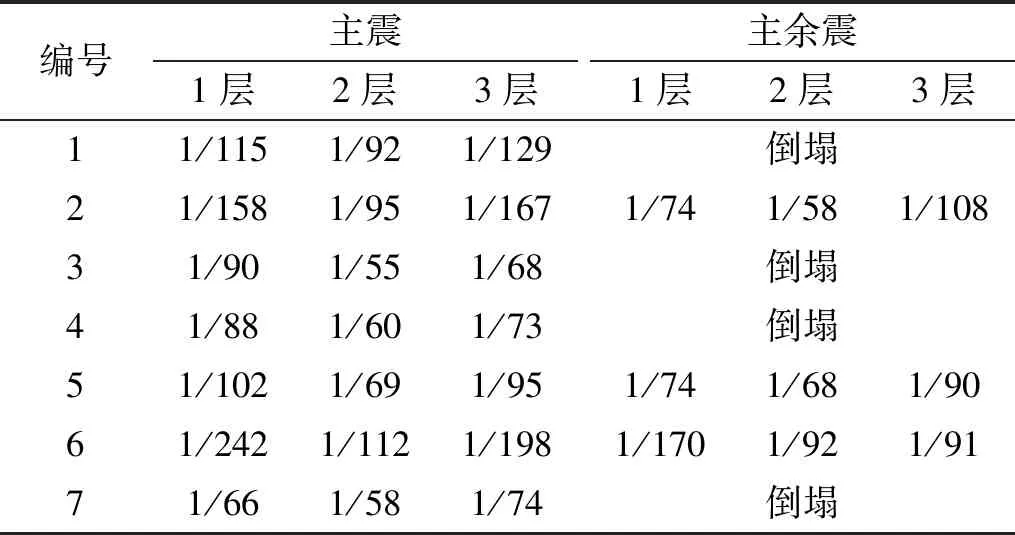
表6 TOB方案模型层间位移角对比(大震)Tab.6 Interstory drift ratio comparison between the TOB programs (Rare earthquakes)
总体来看,拉紧保护模式和阻尼耗能模式均能够提升柔性支撑结构的抗震性能。阻尼耗能模式用原体系10%的阻尼力,在小震和中震到大震过程中持续耗能,在大震中保证了结构性能变化不大。而拉紧保护模式对TOB-AFD的参数要求更高,在大震下开始耗能,为结构提供了更高的抗震能力上限。
6 结 论
本文研究了具有非对称弹塑性模型特征的AFD对主余震耦合作用下柔性支撑结构的减震优化作用。分析结果表明:AFD能够以较小的结构内力为柔性支撑结构提供不退化的刚度和稳定的附加阻尼;在主余震作用下保证结构的安全,全面提升结构体系的抗震性能。主要结论如下:
(1) 分析了传统扁钢TOB结构存在的缺陷。扁钢柔性支撑地震下存在拉伸松弛和压缩松弛问题,导致地震中扁钢TOB松弛与结构性能下降相耦合,在主余震耦合作用下可能发生结构倒塌。
(2) 提取出AFD试验数据中具有典型的非对称弹塑性模型特征的理论模型。分析了非对称弹塑性模型在静摩擦阶段非线性“自拉紧”特性和滑动摩擦阶段均能消除两类松弛问题,并提出了静摩擦和滑动摩擦阶段的理论模型及滑动摩擦阶段的附加阻尼比计算方法。
(3) TOB和AVD并联组成TOB-AFD。提出并分析验证了能够有效保护柔性支撑结构的基于TOB-AFD的拉紧保护模式和阻尼耗能模式。TOB-AFD拉紧保护模式有效防止TOB性能退化,为结构提供更高的减震上限;而TOB-AFD阻尼耗能模式中参数要求低,能够实现稳定耗能,并防止主余震中TOB拉伸松弛,提升结构的抗震性能。
