动载下含预制裂纹砂岩的力学特性及破裂过程研究

2023-02-27张后全黎明镜吴捷豪

振动与冲击 2023年4期

石浩，张后全，宋雷，李明，黎明镜，林钢，施鑫，龙伟，吴捷豪

(1. 安徽理工大学土木建筑学院矿山建设工程安徽省高校重点实验室，安徽淮南 232001；2. 中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏徐州 221008；3. 中煤矿山建设集团有限责任公司，合肥 230000； 4. 巴黎高等师范学院，巴黎 75005)

岩体作为受温度、风化、构造运动等影响的天然材料，含有一定的天然缺陷，尺寸从亚微米到千米不等[1-2]。以挪威西部的Hornelen地区为例，该地区存在一处由砂岩和砾岩填充的盆地，范围大约70×30 km。由于受到冻融循环、海浪冲刷以及地震等的作用，该处地层中的节理、裂隙等缺陷极为发育[3-4]，如图1所示。缺陷的存在导致岩体材料的不均匀性和各向异性，使其具有复杂的受力变形特性及破坏机制[5]。对缺陷岩石力学特性认识不清显然不利于岩石灾害的防治，更难以保障地下工程结构的长效稳定[6-10]。因此，深入研究缺陷岩石(体)的力学特性具有重要意义。根据预制缺陷的数量，目前针对缺陷岩体的研究大致可分为两类。

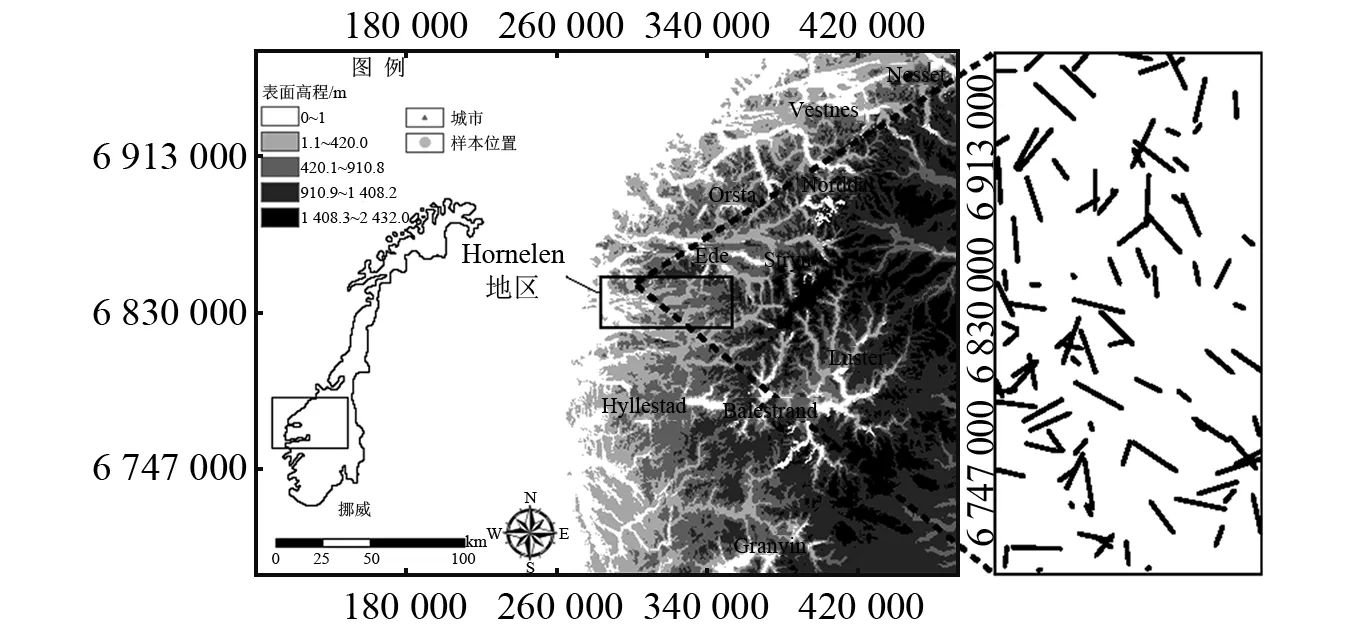
图1 挪威西部霍内伦盆地砂岩天然裂缝系统Fig.1 Outcrop map of the natural fracture system in the sandstone at Hornelen Basin, western Norway

第一类研究预制的缺陷数量一般不大于4，主要通过水力切割(室内试验)或颗粒单元删除(数值模拟)来实现缺陷预制，重在分析单缺陷(裂纹或裂隙)的倾角[11-12]、尺度[13-15]、位置[16]以及多缺陷(裂纹、裂隙及孔洞)间的组合对试件强度及破坏特性的影响[17-20]。如郭庆振[21]利用PFC2D建立了分离式霍普金森压杆(split Hopkinson pressure bar，SHPB)系统的颗粒流模型，研究了节理倾角及节理粗糙度系数(joint roughness coefficient，JRC)对裂纹总数、峰值应力及试样破坏模式的影响规律。李地元等[22]利用SHPB试验系统研究了平行裂隙倾角对大理岩的动态抗压强度、峰值应变及动态弹性模量等力学参数的影响。赵涛[23]结合SHPB试验及软件ANSYS/LS-DYNA模拟方法研究了单裂隙及三裂隙分布对冻结砂岩劈裂应力分布的影响。赵洪宝等[24]认为此类研究设置的缺陷参数过于主观、理想，没有充分考虑天然岩体中的裂纹分布是不规则的，且数量较多，这在一定程度上影响了研究成果的实用价值。

第二类研究预制的缺陷数量成百上千，主要通过真实地层扫描或数值概率分布的方式实现缺陷(裂纹或裂隙)的制作[25-26]。Ma等[27]利用颗粒流(PFC2D)研究了定向分布裂纹(分布裂纹倾角一致)对试件度特性、破坏模式及裂纹发育过程的影响。Bahrani等[28]研究了不同围压条件下裂纹密度对岩石强度的影响。Shi等[29]利用DFN模型生成含随机分布裂纹的砂岩模型，重点研究了预制裂纹数量(number of prefabricated cracks,NPC)对试件抗压强度及弹性模量的影响。Wang等利用PFC2D建立了一尺寸较大的裂纹网络试件作为“父本”，通过在该“父本”中截取不同尺寸的试件进行单轴压缩试验，对裂纹网络试件强度特性的尺度效应进行了研究。上述研究对认识实际岩体的损伤破坏过程具有重要意义，但未考虑天然裂纹长度的幂律分布假设[30-33]。基于此种情况，Shi等利用PFC2D软件模拟研究了裂纹长度幂律指数及NPC的变化对试件强度及破坏特性的影响。第二类研究目前均仅限于静力学领域，关于含分布裂隙(裂纹)岩石试件动力特性的研究尚未见报道，更无考虑裂纹长度及数量分布特征的岩石动力学研究成果。考虑到岩石材料的静、动力学差异极大[34]，无法利用岩石的静力特性代替或精准预测其动力特性[35]。但对于深部煤炭开采，巷道等地下硐室围岩受掘进爆破及老顶来压等的强扰动作用，其动力特性紧密关系着井下工人及设备的安全[36-37]，故目前亟需在此方面开展研究。

因此，本文基于天然裂纹长度的幂律分布假设，利用PFC2D建立SHPB试验系统以及含不同数量分布裂纹的砂岩试件模型，研究在冲击荷载作用下预制分布裂纹数量对砂岩试件变形、强度及破坏等力学特性的影响。

1 SHPB数值模型的建立及其合理性验证

1.1 颗粒流程序

PFC2D是ITASCA公司开发的商业离散元软件，该软件不仅可以很方便地实现裂纹的预制，而且在岩石受力变形及破坏过程的分析方面也具有较好的模拟效果，已被广泛应用于岩土地质工程领域[38-39]。考虑到其模拟优势与本文研究主题相契合，所以本文选择该软件进行裂隙砂岩试件的动力冲击研究。

1.2 数值模型的建立及加载设置

1.2.1 SHPB试验系统组成

利用PFC2D建立的SHPB加载系统模型，如图2所示。由图2可知，该系统主要由4个部分组成，由左至右依次为撞击杆、入射杆、砂岩试件以及透射杆。4部分的尺寸已在图2中标出，而对应的细观参数已在表1中列出，其中撞击杆、入射杆及透射杆的参数参照Shi等[40]的研究，而砂岩试件的参数与王浩等的研究一致。

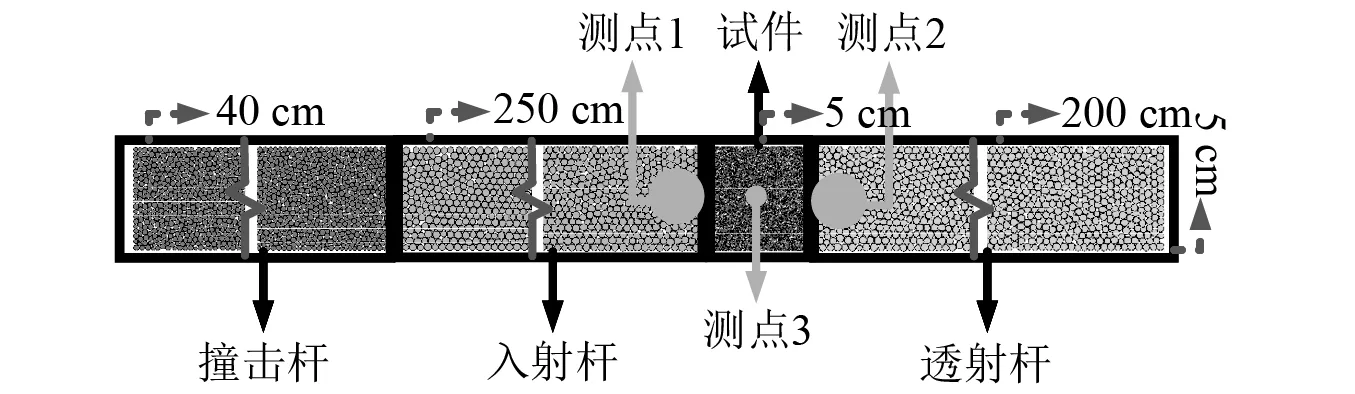
图2 SHPB试验系统PFC模型Fig.2 SHPB experimental system established by PFC software

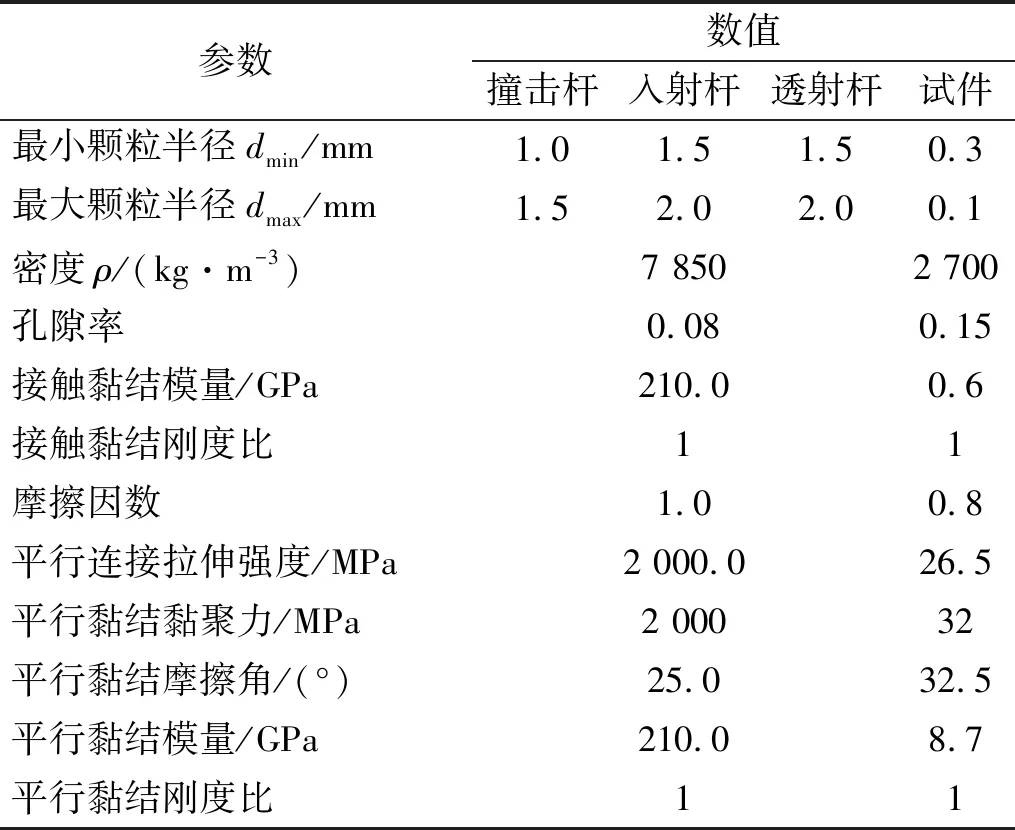
表1 撞击杆、入射杆、透射杆及试样的细观参数Tab.1 Mesoscopic parameters of the striker, incident bar, transmitted bar and specimen

1.2.2 SHPB加载设置及数据收集

SHPB试件加载冲击过程是利用子弹撞击入射杆，从而将冲击波沿入射杆传递至试件处，本文设置的子弹速度为15 m/s。PFC2D软件中测点是利用FISH语言编译测量圆实现的，其原理与现实采用的应变片类似，即收集、处理获得选定模型范围内的颗粒集受力及变形的平均值。根据图2可知，本文模型共计布置了3个测点，并且可以看出测点1及测点2分别布置在紧邻砂岩试件的入射杆及透射杆位置处，而测点3布置于试件中心位置。其中，测量圆1及测量圆2的直径为25 mm，主要用以收集入射波、透射波及反射波，将在1.3节用以验证所建SHPB系统的合理性；而测量圆3的直径为5 mm，主要用以测量试件的受力及变形信息。需要指出的是，测量圆1、测量圆2的直径较测量圆3大，这是因为测量圆需要包含足够数量的颗粒才能保证测量结果的可信性，而测量圆1、测量圆2对应位置的颗粒直径较大，所以需要的测量圆直径也宜较大。

1.3 测试原理及测试波形

为了验证所建模型的可行性，根据1.2节建立的SHPB模型、确定的细观参数以及设置的加载速率进行测试加载，获得的入射波、反射波及透射波形如图3所示。图3中，入射波及反射波由测点1收集获得，而透射波由测点2收集获得。根据1.2.2节可知，测点1的直径达到了25 mm，较大的测量区域导致入射波和反射波在测点范围内发生了波形叠加现象(见图3中的椭圆框区域)。需要指出的是，此模型缺陷是建立在模型精度(颗粒直径)与模型计算时长间矛盾的基础上的；另外，后文研究结果是根据测点3获得的，不会受此模型缺陷影响。

图3 测试加载获得的入射波、反射波及透射波Fig.3 Incident wave, reflected wave and transmitted wave obtained by test

从图3可以看出，入射波、反射波及透射波的峰值分别约为175 MPa，80 MPa及100 MPa。根据弹性杆理论，岩石试件左右两端的荷载应相等，对应入射波与反射波之和应与透射波平衡，这是SHPB动态压缩试验成功的先决条件[41-45]。据此对图3中的波形进行截取，利用三波法分析所建SHPB数值模型的动力平衡情况，如图4所示。由图4可以看出，入射波与反射波之和与透射波基本重合，说明所建模型能较好地满足动力平衡条件，保障了第3章模拟研究结果的有效性。

图4 SHPB数值模型的动力平衡检查Fig.4 Dynamic stress equilibrium check of SHPB numerical model

2 含分布裂纹试件的制作

2.1 裂纹长度的幂律分布方程

De Dreuzy等、Hunziker等以及Ignatovich等研究者均认为天然裂纹长度服从幂律分布假设，方程为

(1)

式中：lc与xc分别为裂纹长度及其自变量；a(>0)为常数且a=zeta(1/b-1)[46]，而b(>1)为幂律分布指数。

为了获得特定的裂纹长度幂律分布，需先给出预制裂纹的最大、最小长度lc,max，lc,min以及幂律指数b。然后根据式(1)确定裂纹长度的幂律分布形式。最后，通过给定NPCnp，利用线性插值(理论)或概率分配(数值模拟)的方式便可以获得具体的裂纹长度。

2.2 分布裂纹预制

在PFC2D中，裂纹作为平面、有限尺寸且离散的结构单元是通过DFN(discrete fracture network)模块实现预制的。本文设置的裂纹倾角及位置范围分别为0～180°及试件所在区域，均服从随机均匀分布。裂纹长度服从幂律排布，幂律指数为2.5,长度范围为0.5～10 mm。

本文研究主要考虑NPC对试件动力特性的影响，按照2.1节幂律分布理论建立的数值模型根据NPC的不同共计分为6组，各组试件包含的NPC分别为25，50，100，150，200及300。参照实际模拟得到的各组试件强度的离散性情况，每组建立3～4个试件，如图5所示。图5中，试件左上角字母与数字的组合为试件编号。需要特别说明的是，每组试件的裂纹分布信息都是一致的，包括裂纹长度范围、角度范围、分布范围、幂律指数以及NPC等，区别在于DFN模块调用次数(与试件编号中的末尾数字一致)的变化。当DFN模块调用次数一定时，对应生成的裂纹分布形式是固定的，即模拟计算完全可重复；但当DFN模块调用次数发生改变，裂纹长度将根据分布方程再次随机赋值，同时裂纹倾角、位置也再次发生随机分布。另外，预制裂纹采用平滑节理模型(smooth joint model，SJM)，模型的默认参数已在表2中列出。

图5 含不同NPC的砂岩试件模型Fig.5 Sandstone specimen models with different NPCs

表2 平滑节理模型的力学参数Tab.2 Mechanical parameters of SJM

3 模拟结果及分析

按照1.2.2节给出的加载设置，依次对图5中的21个试件进行了模拟加载，收集获得了试件的应力-应变曲线、AE曲线以及不同应力水平下的裂纹扩展信息等，在本节中进行针对性分析。

3.1 砂岩试件应力-应变响应特性

模拟获得的各试件的应力-应变曲线，如图6所示。由图6可以看出，随NPC的增加，试件强度整体上呈减小趋势。并且，当NPC较少时(np=25，50)，各组试件的应力-应变曲线在峰前基本重合，强度也无明显差别；但随NPC的增加(np=100，150，200，300)，各组试件的强度、弹性模量离散性逐渐增大，并且峰后应力的降低过程也更加复杂。

图6 含不同NPC试件的应力-应变曲线Fig.6 Stress-strain curves of specimens with different NPCs

当NPC为25及50时，试件峰后应力基本沿原路返回，为了避免曲线相互叠加影响读者观察，仅对试件S25-2的峰后应力跌落过程进行了展示(见图6(a))。可以看出，对于试件S25-2，其发生压缩变形后又发生了应变恢复，整个过程似乎是弹性的(见图6(a))；这说明加载完成后，测点位置处并没有发生显著破坏，而是以完整岩块的形式存在。但当NPC>100时，峰后应力跌落过程多对应应变的持续增长(见图6(c)～图6(f))；这说明在加载过程中，对应试件的测点位置处已经发生了一定程度的损伤，但这不妨碍对应力的准确量测。

另外，可以看出所有试件在峰前阶段其应力点都呈稠密-稀疏-稠密的分布模式，如图6(b)中的标注所示。这显示，在加载过程中试件的变形速率并不一致，而是受到应力波传播的影响不断发生变化。在压缩应力波完全到来前，试件受力较小变形缓慢；在应力波经过时试件受力增加、变形加快；而后应力波发生透射及反射逐渐减弱，对应试件的变形速率放缓。

3.2 砂岩试件强度及变形特性

根据图6可绘出试件强度随NPC的变化规律，如图7所示。由图7可以看出，随NPC由25增至300的过程中，试件强度σc由最大约86 MPa逐渐降低至最小22 MPa，降低幅值超过60 MPa；并且随NPC的增加，试件的强度离散性逐渐变大，对应均值点的误差棒长度增加。具体地，当NPC分别为25，50，100，150，200及300时，对应的各组试件的强度均值分别为86.13 MPa，82.71 MPa，70.78 MPa，67.48 MPa，65.84 MPa及46.14 MPa，而最大强度差分别为0.54 MPa，4.58 MPa，6.79 MPa，16.39 MPa，18.08 MPa及41.91 MPa。通过对各组试件的强度均值进行拟合发现，随NPC的增加，试件强度均值近似呈线性减小趋势，拟合度达0.948(见图7)。

图7 试件强度随NPC的变化规律Fig.7 Variation of specimen strength with NPC

根据图6也同样可以获得试件割线弹性模量E随NPC的变化规律，如图8所示。从图8可以看出，试件的弹性模量整体上也随NPC的增加而减小，而弹性模量的离散性随NPC的增加而增加。具体地，当NPC分别为25，50，100，150，200及300时，对应的各组试件的弹性模量均值分别为10.57 GPa，10.49 GPa，10.33 GPa，10.13 GPa，8.92 GPa以及7.95 GPa，而最大弹模差分别为0.04 GPa，0.17 GPa，0.67 GPa，1.03 GPa，3.97 GPa及6.85 GPa。通过对各组试件的弹模均值进行拟合发现，试件弹模均值随NPC增加的变化规律更接近三次方程(拟合度达0.955，见图8)，利用线性方程拟合的拟合度仅有0.856，但刨除图8中离散性较大的数据点1及数据点2，线性拟合的拟合度高达0.992(见图8)。

图8 试件弹性模量随NPC的变化规律Fig.8 Variation of specimen elastic modulus with NPC

3.3 砂岩试件声发射特性

利用FISH语言可提取试件加载过程中的新生裂纹数量增长情况，进而可处理获得特定长度应变下的裂纹事件数(本研究对应的应变增量为0.004 7‰)，即对应室内试验的声发射(acoustic emission，AE)事件数。由于本研究建立的试件模型较多(见图6)，难以对所有试件都进行展示分析，在此选择各组试件中强度最接近强度均值的试件进行针对性研究，对应的试件编号分别为S25-1，S50-2，S100-1，S150-1，S200-2以及S300-3。所选试件加载破坏过程对应的新生裂纹数量增长曲线及AE事件数情况如图9所示。

根据图9可知，新生裂纹数量曲线在峰前均呈三段式，在应变接近为0时，裂纹数量增长速度较快，曲线斜率接近为1。而后在较小的应变范围内(小于峰值应变的1/10)，裂纹数量增长速度逐渐放缓直至平稳增长，平稳增长时对应的曲线斜率均小于1/2；特别是当NPC为25时，对应的曲线斜率接近为0。但当加载到峰值应变的80%左右时，裂纹数量增长速度显著增加，曲线斜率再次接近为1，特别是当NPC≤150时尤为明显(见图9(a)～图9(d))。结合对图6的分析可以发现一个奇怪的现象，即当试件应变增长较快时，对应产生的裂纹数量较少，但当应变增长较慢时，对应裂纹大量、集中产生。这是由于在冲击荷载作用下试件变形破坏并不均匀，特别是试件左右两侧分别与入射杆及透射杆接触(见图2)，接触界面位置材料刚度差异极大，试件变形缓冲空间小易发生破坏；而测点3位于试件中心位置，应力波作用下该处材料变形协调性较好、缓冲空间大，对应试件变形速率高(见图6及图9)，可预测加载后至峰值应力后试件中心位置处的材料完整性较左右两侧好。

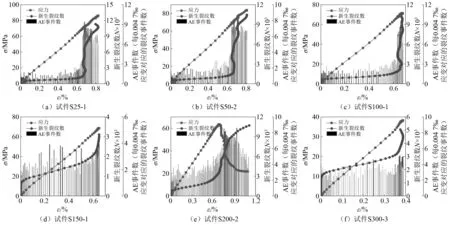
图9 NPC影响下试件声发射事件演化规律Fig.9 Evolution of AE events under the influence of NPC

通过数据提取可得，试件S25-1，S50-2，S100-1，S150-1，S200-2以及S300-3达到峰值应力时对应的新生裂纹数分别约为1.07×104，1.02×104，9.39×103，2.91×103，3.57×103以及4.39×103，总体上呈先减小后增加的变化规律，但因为数据分析涉及的试件较少，并且NPC≥100对应试件的强度离散性较大(见图7)，故该结论尚需进一步验证。另外，对于试件S25-1，S50-2及S100-1，其峰前的AE事件分布不均匀，当应力低于约80%试件强度时，AE事件基本均小于3/(0.004 7‰应变)；但当应力达到80%试件强度时，AE事件显著增加，最大值接近10/(0.004 7‰应变)。而对于试件S150-1，S200-2及S300-3，其峰前AE事件皆相对均匀，最大值接近3/(0.004 7‰应变)。

3.4 砂岩试件破坏特性

与3.3节一致，本节同样选择试件S25-1，S50-2，S100-1，S150-1，S200-2以及S300-3作为代表，分析NPC对试件破坏特性的影响。图10展示了所选试件在不同应力水平下的裂纹扩展情况。

结合图9及图10可以看出，当试件加载至10%峰值应力处时，新生裂纹增长较快，而试件中部的应变增速较慢(见图9)。可以判断出此时压缩应力波传播至试件左侧边缘，在应力波作用下该位置发生损伤破裂，对应产生大量离散裂纹，如图10中各试件在10%峰值应力处对应的裂纹分布。

随着压缩应力波的持续向右传播，各试件中的新生裂纹位置也逐渐沿应力波传播方向分布，如图10中各试件在10%峰值应力及峰值应力处的裂纹分布情况。由图10可以看出，各试件加载到峰值应力的时间t均在10～20 μs内，并且整体上随NPC的增加呈减小趋势。在峰值应力处，新生裂纹基本只分布在试件的左半侧。另外，试件中的NPC越多，在峰值应力处产生的裂纹数量越多；通过对图9进行提取，可得峰值应力处试件S25-1，S50-2，S100-1，S150-1，S200-2以及S300-3的新生裂纹数，分别为1.609×103，1.776×103，1.821×103，2.121×103，3.569×103及3.511×103，呈随NPC的增加而增加的变化规律。对于试件S25-1，S50-2，S100-1及S150-1，新生裂纹依然是以散斑的形式呈现，对应的AE事件曲线基本呈单峰值、高极值形式(见图9)；而对于试件S200-2及S300-3，其内部已经出现了相对明显的裂纹集聚现象，试件内部多个核裂纹间已相互连通，对应的AE事件曲线基本呈多峰值、低极值形式(见图9)。

当加载到软化阶段时，可以看出试件内部裂纹显著增加，试件S25-1，S50-2，S100-1及S150-1内部也出现了明显的裂纹集聚及联通现象。并且，试件右侧边缘因与透射杆相互作用发生了明显破坏。当试件加载至最终破坏时，可以看出各试件均由多个尺度不一的岩块组成，已无法视作连续介质，新生裂纹分布均呈片层状。并且可以看出，试件S25-1，S50-2，S100-1及S150-1中的新生裂纹分布均靠近试件边界，试件中心位置分布极少，在该位置形成了较为完整的岩块。但对于试件S200-2及S300-3，由于其内部NPC较多，试件的弹模或刚度较小，能够较充分的吸收压缩应力波，导致应力波传播至试件右侧边界时已发生显著减小，试件与透射杆间的相互作用较为平和，故在试件右侧只产生了较少数量的裂纹。

图10 NPC影响下试件裂纹扩展过程Fig.10 Crack propagation process of specimen under the influence of NPC

利用自主编译FISH程序，提取获得了图10中各试件加载至最终破坏时的新生裂纹倾角，进而可绘制出裂纹倾角的玫瑰分布图，如图11所示。由图11可以看出，所有试件的新生裂纹倾角分布图形基本都沿x=90°对称，并且新生裂纹倾角主要分布在0～30°以及150～180°；也就是说，试件在冲击荷载作用下主要沿应力波传播方向发生破裂。另外，随NPC的增加玫瑰图横向尺寸与竖向尺寸的比值逐渐减小；当NPC=25时，玫瑰图横向尺寸约为竖向尺寸的6倍，但当NPC为300时，该值仅为3左右，新生裂纹分布较为均匀。这说明在相同的冲击荷载作用下，试件损伤程度越大越不易控制裂纹的扩展方向。结合对图10的分析可知，这是由于试件损伤程度越大越能有效地吸收应力波，导致试件损伤集中发生在某一较小的区域内(试件S300-3的左半侧，见图11(f))。显然，试件中区域破裂程度越大越可能出现裂纹倾角的均匀(或紊态)分布。