基于RPCA低秩稀疏分解的循环频率检测方法

王 冉，余龙靖，余 亮，蒋伟康

(1. 上海海事大学 物流工程学院, 上海 201306; 2. 上海交通大学 机械系统与振动国家重点实验室，上海 200240)

循环平稳是处理随机信号中隐藏的周期性现象的一个强大工具。循环平稳信号是指一类特殊的非平稳信号，其性质是随机的，但在统计中表现出周期性[1]。旋转机械由于其旋转运动特点，其产生信号具备周期时变特性，是典型的循环平稳信号。目前，循环平稳信号处理方法已广泛应用于旋转机械故障诊断、机械系统识别和盲源分离等[2]。明阳等[3]提出了一种基于循环维纳滤波器和包络谱分析的方法对滚动轴承微弱故障特征进行提取。近年来通过改善循环平稳理论进行旋转机械故障诊断仍是一个热门话题[4-6]。Chen等提出了一种新的结合循环谱相干和深度学习的故障诊断方法，将滚动轴承故障信号的二维循环谱相干图与卷积神经网络(convolutional neural network, CNN)结合完成滚动轴承的故障诊断。

在循环平稳信号处理方法的应用中，循环频率的检测至关重要。例如：基于循环平稳分析实现机械源分离的前提是利用循环频率设计滤波器。在旋转机械的故障诊断中，循环频率往往就是旋转部件的故障特征频率，对轴承、齿轮等部件的振动信号进行循环平稳分析的主要目的就是提取循环频率从而确定设备的故障类型。在工程中的许多其他问题也与循环频率的检测息息相关。例如：Umut等[7]利用轮船声信号具备的二阶循环平稳特性，通过对水听器测量的声信号进行循环频率检测来探测轮船；Antoni等[8]利用循环调制相干性从测量信号的循环平稳特征中检测水面舰船。此外，Li等[9]利用离心泵振动信号的流动诱导效应的循环平稳特性，使用循环平稳方法对其进行检测。在上述应用中，为了检测到有效的循环频率及其高阶谐波，常规的基于循环平稳特征的方案倾向于简单地将信号特征的值与预定阈值进行比较。然而，当信号被噪声干扰时，这样的方案将导致检测性能大幅下降。

主成分分析(principal component analysis, PCA)是数据科学领域中获取和分析数据的基本工具，其基本思想就是从高维数据中提取出低维的有效数据。但主成分分析对于噪声干扰非常敏感。鲁棒主成分分析(robust principal component analysis, RPCA)是为了提高主成分分析的鲁棒性而提出的用于矩阵低秩稀疏分解的方法。鲁棒主成分分析的本质是将一个已知的采样数据矩阵M∈M×N分解成一个低秩矩阵L∈M×N和一个稀疏矩阵S∈M×N，其中，M×N表示大小为M×N的实数矩阵。Candès等[10]通过将一般矩阵分解为低秩和稀疏矩阵解决了鲁棒性问题，为信号处理和计算机视觉应用提供了合适的框架，并被广泛应用于声学信号处理[11-12]与机器学习[13-14]中。Yu等[15]利用RPCA对轴承振动信号短时傅里叶变换得到的时频图进行分解，从严重噪声污染的滚动轴承振动信号中提取瞬态信号以进行故障诊断。

针对强噪声干扰下难以准确检测循环频率的问题，本文提出了一种强干扰下将基于鲁棒主成分分析(robust principal component analysis, RPCA)的低秩稀疏分解技术应用于循环谱密度(cyclic spectral density, CSD)矩阵从而进行循环频率检测的方法。该方法首先计算强背景噪声下的循环平稳信号的CSD矩阵，利用RPCA将循环谱密度矩阵分解为代表噪声干扰的低秩矩阵和包含循环频率特征的稀疏矩阵，再利用稀疏矩阵构建检测函数对循环频率进行自动检测。仿真结果验证了该方法在强噪声干扰下进行循环频率检测的优越性，并可根据检测循环频率各高阶谐波的ROC曲线为不同信噪比条件下选择检测阶数提供参考。最后将该方法应用在滚动轴承早期故障检测上，试验结果与常用的包络谱和谱峭度(spectral kurtosis, SK)方法[16-18]对比以证明该方法在早期故障诊断应用中的优越性。

1 理论基础

1.1 循环谱密度

循环平稳信号是一类特殊的非平稳信号，其统计特性随时间周期性变化。包含额外信息的隐藏周期性表现在循环平稳信号中。

对于循环平稳信号x(t)，其时变自相关函数Rx(t,τ)为

(1)

Rx(t,τ)=Rx(t+T,τ)

(2)

(3)

式中，α为循环频率，且α=m/T,m=1,2,3,…。对式(3)中的时延τ作Fourie变换即可得到CSD函数，也称谱相关密度(spectral correlation density, SCD)函数

(4)

式中，f为频谱频率。CSD也可看作是时变自相关函数Rx(t,τ)的二阶Fourier变换，因此也可写为信号x(t)左右移频α/2的两信号的互谱密度

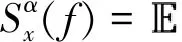
(5)

循环谱密度函数表示每个离散循环频率分量α上频谱频率f的功率分布。

1.2 鲁棒主成分分析

鲁棒主成分分析算法是由Candès等提出的实现图像背景与前景分离的重要技术之一。RPCA采用低秩稀疏模型，将数据矩阵分解为低秩矩阵和稀疏矩阵。设L为低秩矩阵，S为稀疏矩阵，M为原始矩阵，故RPCA 的低秩稀疏分解可以看成优化问题

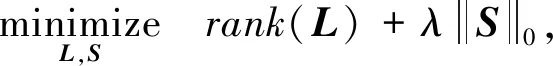
(6)

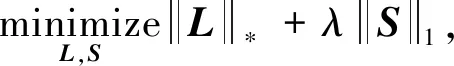
(7)

2 基于RPCA的循环频率检测方法

对于一个循环频率为αk(k=1,2,3,…)的循环平稳信号x(t)，其循环谱密度矩阵是由离散分布在对应循环频率列上的稀疏值组成的，因此CSD中的循环频率特征具有稀疏特性。且平稳噪声的CSD具备低秩特性。本文针对噪声和循环平稳信号的CSD矩阵分别具有的低秩和稀疏特性，提出一种对CSD矩阵低秩稀疏分解的方法。该方法利用RPCA对强干扰下循环平稳信号的CSD矩阵M进行低秩稀疏分解的方法，将噪声的CSD建模为低秩矩阵L，循环平稳信号的CSD建模为稀疏矩阵S，进而利用稀疏矩阵S构建检测器进行循环频率的检测。方法的具体流程如图1所示。

图1 基于RPCA的循环频率检测方法流程Fig.1 The flowchart of RPCA-based cyclic frequency detection method

对于输入的带有强干扰的循环平稳随机信号，首先利用式(4)计算其循环谱密度矩阵。其次利用RPCA对CSD矩阵进行低秩稀疏分解。然而值得注意的是，稀疏矩阵S在λ较小时经常被噪声污染(这表明一定量的噪声被分解为稀疏分量)。因此，可以进一步使用滤波器来修正最终结果，其形式为

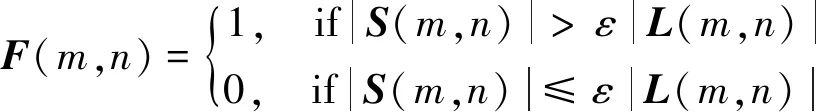
(8)

式中，ε为控制|S(m,n)|和|L(m,n)|幅度增益比的参数，本文中取定值ε=1。通过计算哈达玛积(Hadamard product)E=F⊙S可以通过滤波减少稀疏矩阵S中的噪声干扰从而得到稀疏性更强的增强稀疏矩阵E。最后，利用得到的增强稀疏矩阵E构建检测函数

(9)

式中：TR∈Ck；分子表示增强稀疏矩阵E第k列元素之和；分母表示原始CSD矩阵M第k列的均值。最后通过一个带有固定阈值的peak-picking算法检测出检测函数的峰值点即循环频率。

3 仿真分析

为验证方法的有效性，用带有强噪声干扰的循环平稳仿真信号输入对其进行循环频率检测。仿真的循环平稳信号以轴承外圈故障模型为参考，其信号模型为

(10)

式中：s(t)为局部点蚀失效引起的静态振荡信号；T为振荡发生周期；n(t)为干扰噪声；β为共振阻尼衰减系数；fn为共振频率。仿真时，采样频率为10 000 Hz，共有10 000个采样点。振荡发生周期T=0.05 s，故循环频率为20 Hz。共振阻尼衰减系数β=500且共振频率fn=3 600 Hz。

为验证在低信噪比条件下的检测性能，为仿真信号加以信噪比(signal-to-noise ratio，SNR)为-20～0 dB的高斯白噪声分别进行检测。图2为加了RSN=-10 dB 噪声的仿真信号的波形、循环谱密度图。

图2 加噪仿真信号(RSN=-10 dB)Fig.2 The noisy simulated signal (RSN=-10 dB)

由图2(b)中加噪信号的CSD图可以看得，在对仿真的循环平稳信号加入了RSN=-10 dB的高斯白噪声后，循环平稳特征已被干扰成分所掩盖。对该加噪信号矩阵进行RPCA低秩稀疏分解，其中参数λ=0.06。并进一步利用式(8)所示的滤波器对得到的稀疏分量进行增强，参数ε=1。分解得到的低秩分量和增强稀疏分量如图3所示。

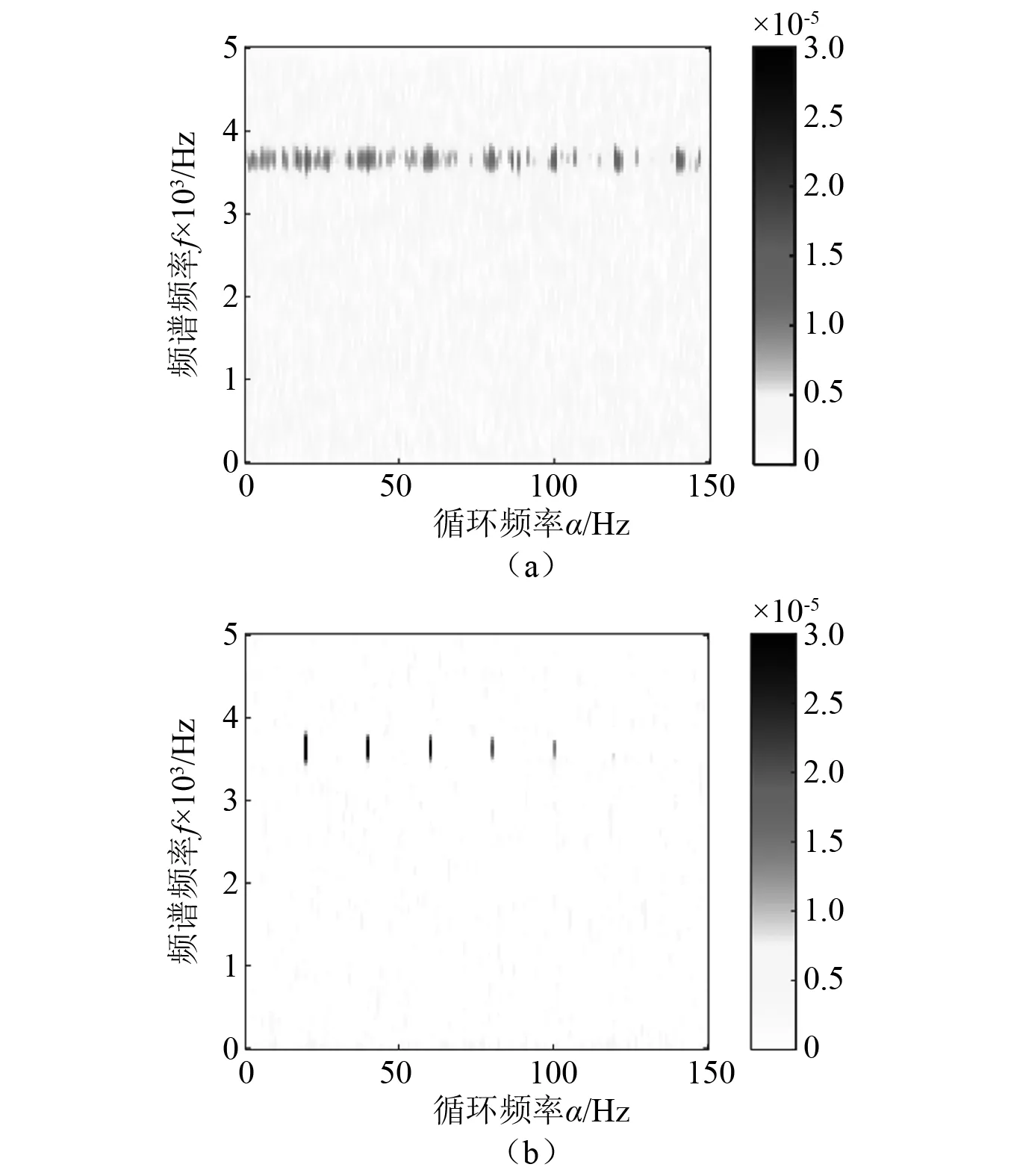
图3 加噪仿真信号(RSN=-10 dB)低秩稀疏分解结果Fig.3 The low-rank and sparse decomposition results of noise-added simulation signal (RSN=-10 dB)

从分解结果可以看出在噪声干扰的信噪比达到-10 dB 时仍可在稀疏分量中将背景噪声几乎分离，且在稀疏分量中可以明显看出循环频率及其高阶谐波的位置。在得到带有循环平稳特征的增强稀疏矩阵后，利用式(9)构建循环频率的检测函数。图4(a)为直接使用原始CSD构建检测函数的检测结果，图4(b)为检测函数经过阈值为0.1的peak-picking算法检测到的峰值点(即循环频率及其高阶谐波点)。由图4可以看出在RSN=-10 dB时本文提出的检测方案仍可以准确地检测到循环频率(20 Hz)及其前2～5阶倍频且相较于原始CSD直接检测的效果优越。

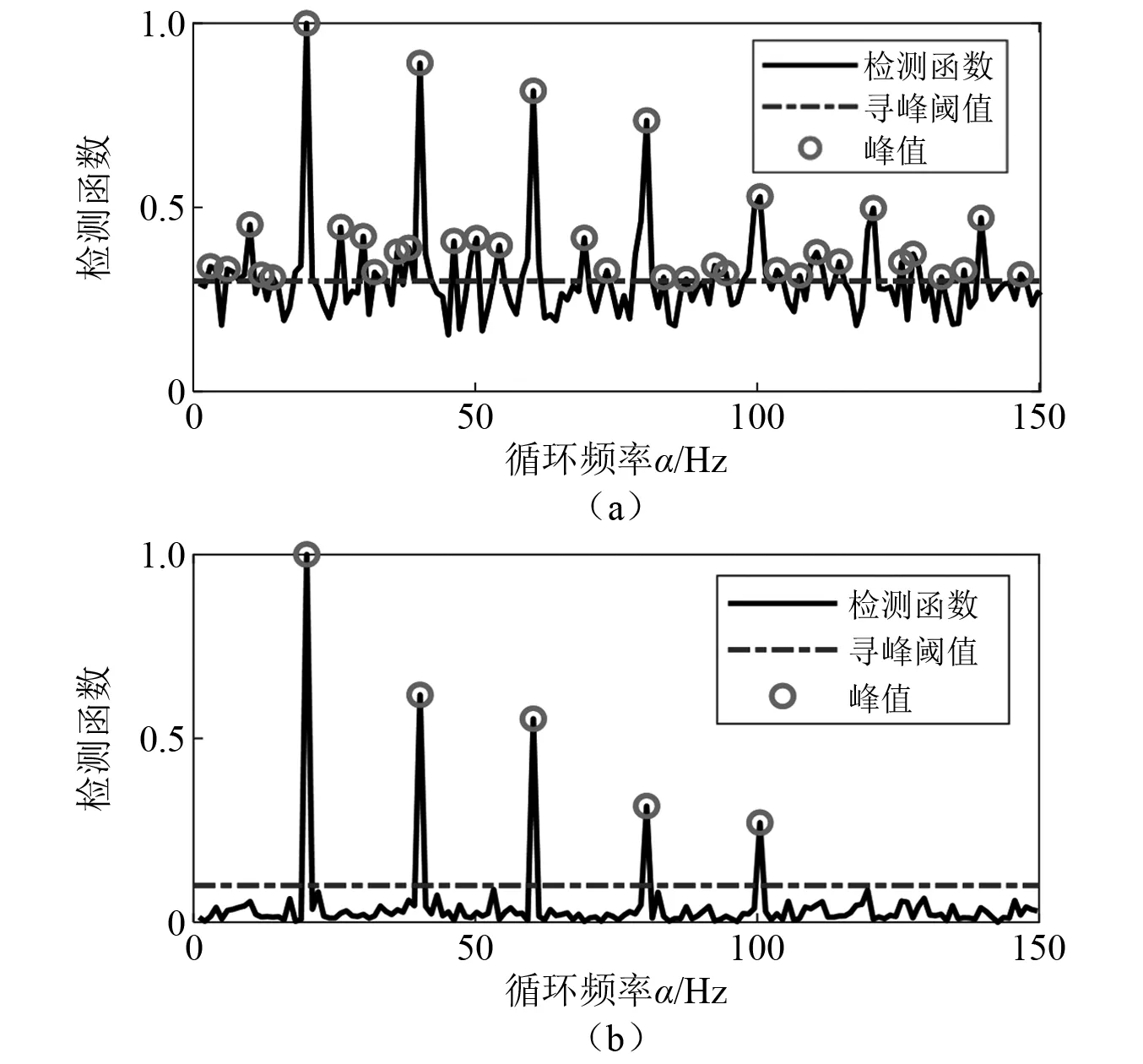
图4 循环频率检测结果Fig.4 The result of the cyclic frequency detection

为进一步评估所提出的循环频率检测器对于噪声干扰的鲁棒性，本文利用蒙特卡洛模拟，在各SNR噪声干扰下分别对检测循环频率1～5阶谐波频率进行100次检测模拟。通过Pd=Md/Mtot来计算检测概率绘制ROC曲线，其中Md和Mtot为检测到循环频率及其高阶谐波的次数和检测的总次数。本文提出的检测器的ROC曲线如图5所示。结果表明了在强噪声干扰下检测概率方面的优越性。该ROC曲线也可为不同信噪比条件下选择检测阶数提供参考。根据检测循环频率各高阶谐波的ROC曲线，为保证检测准确率高于90%的条件下尽可能多地检测循环频率阶数，可在RSN≥-10 dB 时检测5阶谐波频率，-11 dB≤RSN<-10 dB时检测4阶谐波频率，-14 dB≤RSN<-11 dB时检测3阶谐波频率，-15 dB≤RSN<-14 dB时检测1阶谐波频率。

图5 蒙特卡洛模拟ROC曲线Fig.5 The ROC curve of Monte Carlo simulation

4 试验验证

滚动轴承故障信号是典型的循环平稳信号，故利用本文提出的方法可以被应用到滚动轴承故障诊断中。为进一步验证方法的有效性，本文将所提出的方法应用于滚动轴承加速疲劳寿命试验数据中以实现滚动轴承早期故障的检测。

4.1 试验设置

本试验为在杭州轴承试验研究中心支持的加速轴承寿命测试仪(ABLT-1A)上进行的加速轴承从运行到故障的全寿命测试。试验装置主要由试验台、滚动轴承架、传动系统、加载系统、计算机控制系统和数据采集系统组成。整个试验设备如图6所示。试验台在由交流电机驱动的单轴上同时承载4个滚动轴承。传感器安装简图如图7所示。轴转速设置为3 000 r/min，轴上的径向载荷增加为12 744 kN。每分钟采集一组 0.8 s的数据，采样率为25.6 kHz。被测轴承型号为6307，根据轴承的结构参数和转速，可由运动学公式计算出轴承失效的特征频率，如表1所示。

图6 ABLT-1A型轴承寿命强化试验机Fig.6 Accelerated bearing life tester, ABLT-1A

图7 传感器安装简图Fig.7 The installation diagram of the sensor

表1 6307滚动轴承特征频率Tab.1 Characteristic frequencies of rolling bearing 6307

4.2 试验结果

在加速轴承故障寿命测试中，总共测试了8个滚动轴承。作为第一个故障轴承，轴承B12不易受到其他轴承的干扰。在我们的试验中，选择失效滚动轴承B12的数据作为试验对象。图8为B12轴承的全寿命有效值(RMS)变化曲线(RMS是工程上使用较为广泛的设备衰退评估指标)。由图8可知，轴承RMS值在2 302点发生突变。

图8 B12轴承全寿命有效值RMSFig.8 The RMS of B12 bearing life cycle

在这种情况下，将考虑整个寿命周期的第2 297 min 的数据。图9显示了2 297 min原始信号的时域波形和包络谱分析。显然，无法从波形中获取轴承的故障信息。分析信号的包络谱如图9(a)所示，由包络谱只能看见内圈的故障特征频率一阶基频且噪声干扰成分大，影响故障检测。

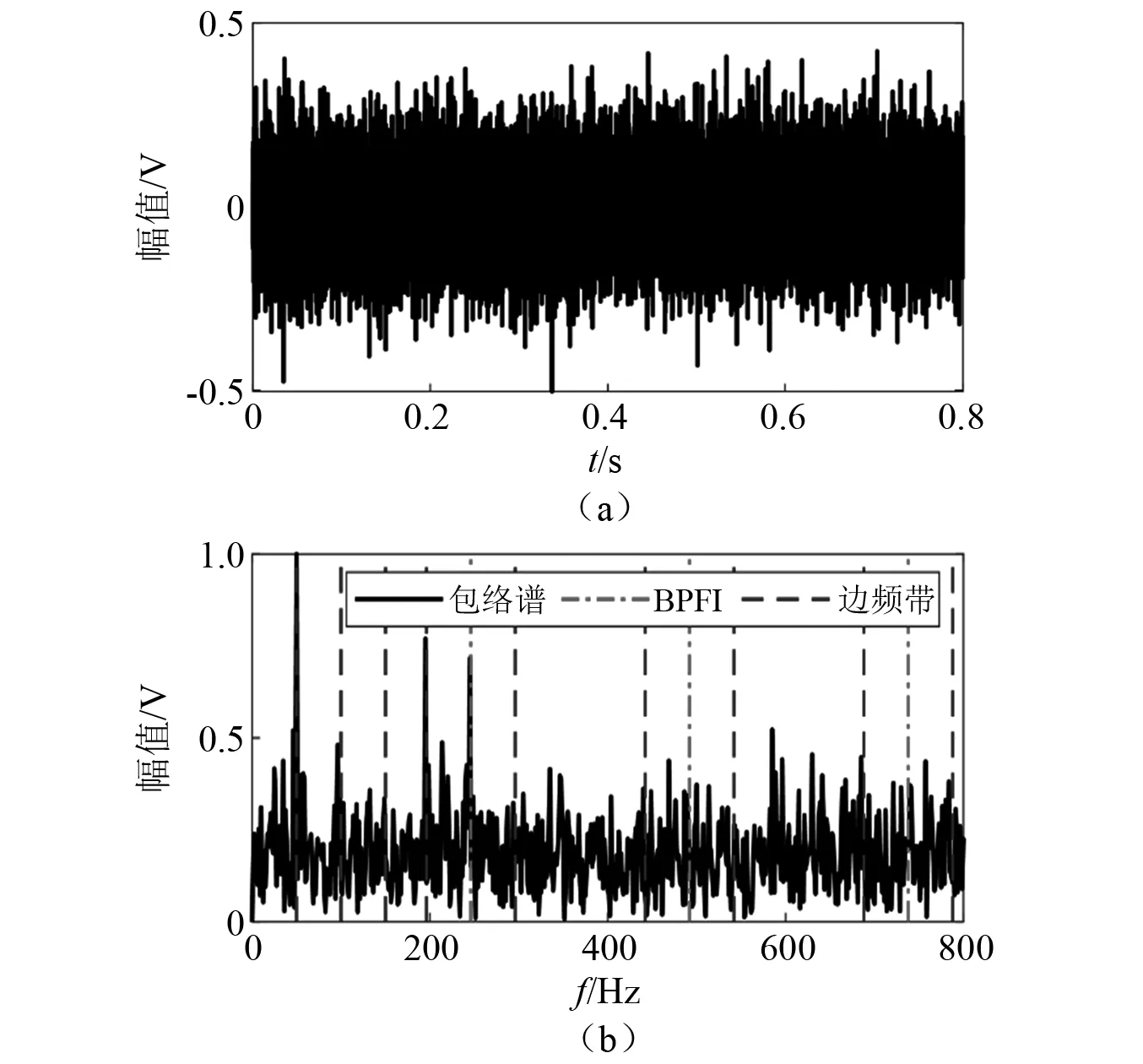
图9 B12轴承全寿命周期的第2 297 min的数据Fig.9 The data at the 2 297th minute of the full life cycle of the B12 bearing

使用所提出的方法对分析信号进行循环频率检测，其CSD与分解后的增强稀疏分量如图10所示。如图10(a)所示，原始信号的CSD中轴承的的故障特征成分十分微弱且被强干扰成分掩盖，无法从中检测故障。经本文所提出方法低秩稀疏分解后并增强后的稀疏分量如图10(b)所示，其中参数λ=0.025，ε=1。从图中可以明显地看出轴承内圈故障特征成分以及转频的边频带成分。

图10 分析信号CSD图与低秩稀疏分解结果Fig.10 The CSD of analysis signal and low-rank and sparse decomposition results

最后，对于得到的增强稀疏分量，使用式(9)计算检测函数并采用阈值为0.1的peak-picking算法进行检测，检测的结果如图11所示。

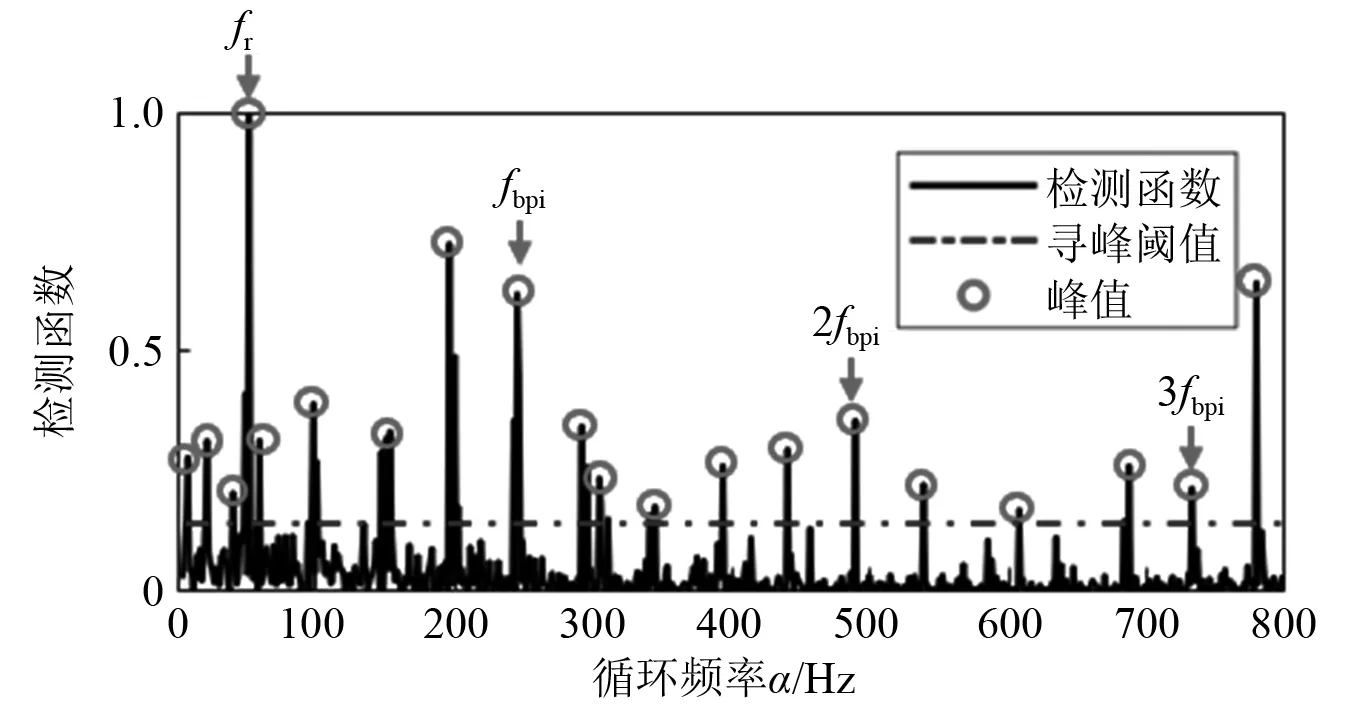
图11 循环频率检测结果Fig.11 The result of the cyclic frequency detection

在寻峰算法找到的峰值中，可以找到内圈故障频率fbpi及其倍频成分，且可以明显地看到转频调制的边频带成分，虽有得到一些干扰频率成分，但已可以充分地检测到轴承的内圈故障。将本文提出方法的检测结果对比于图9(b)的包络谱结果，其效果有明显的提升。该方法在2 297 min即可检测到轴承故障，比利用RMS值检测故障的时刻早。这充分地说明该方法在滚动轴承早期故障检测中的优越性。

为进一步证明该方法在滚动轴承早期故障检测中的优越性，本文使用谱峭度的方法对第2 297 min数据故障特征提取的结果作为对比。

与共振频带相关的信息最丰富的频带可以从图12(a)中所示的谱峭度图中获得，由虚线圆圈突出显示。信息最丰富的频谱频带的中心频率fc=2 333.3 Hz，带宽为bw=133.3 Hz。随后利用带通滤波器将该信息最丰富的频带滤出，滤波后信号的时域波形如图12(b)所示。接着对该滤波信号进行包络谱分析，如图12(c)所示。由滤波信号包络谱可以看到，经谱峭度方法滤波后分析的方法得到的包络谱中仅可以看到内圈故障特征频率的一阶谐波，在更高阶的频率上并没有峰值存在。将此结果对比图11中本文所提出方法的检测函数，可以进一步反映出本文提出方法的优越性。

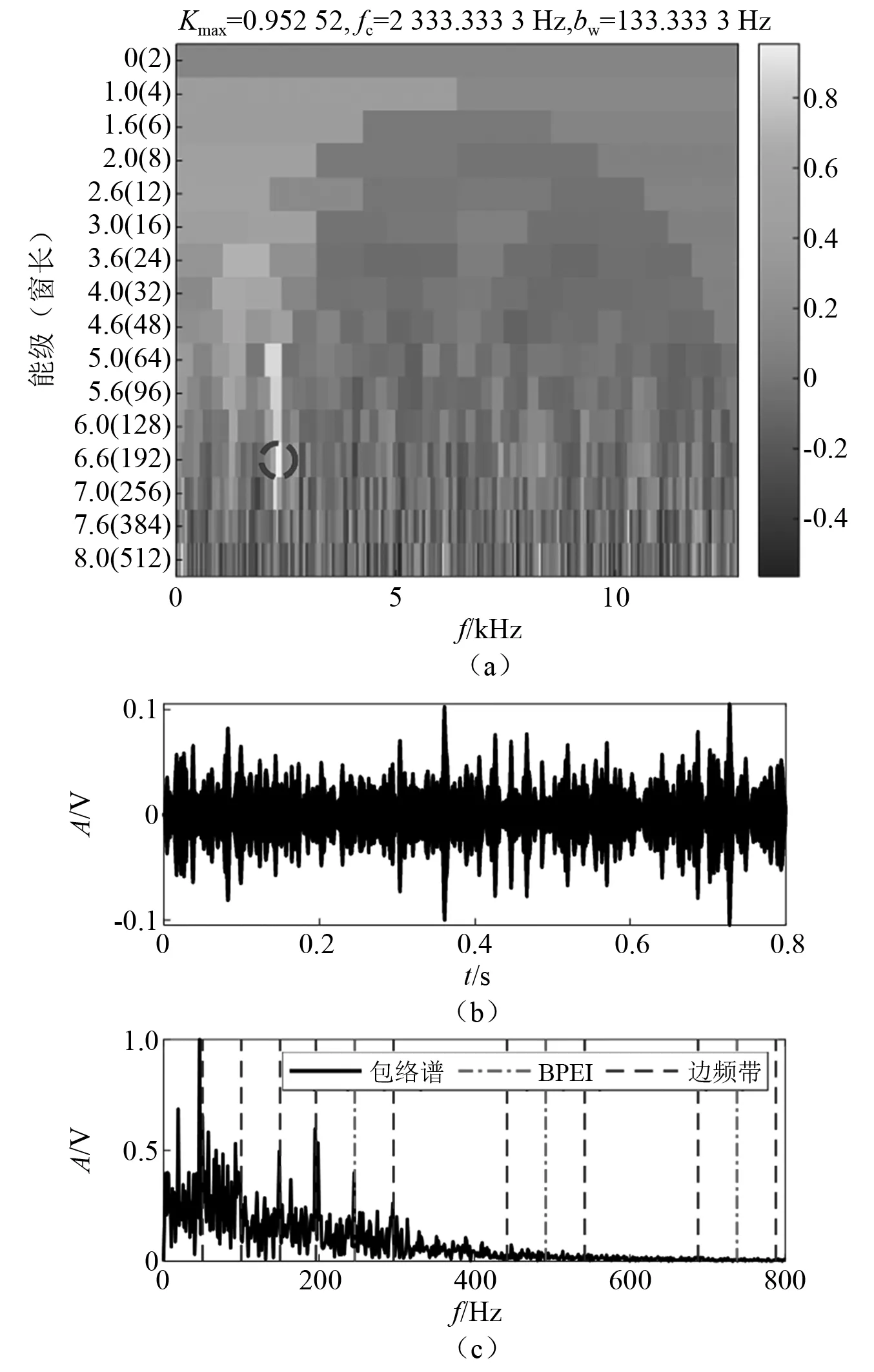
图12 谱峭度分析Fig.12 The results of spectral kurtosis

5 结 论

针对低信噪比条件下循环频率难以检测的局限，本文提出了一种低信噪比下将基于鲁棒主成分分析的低秩稀疏分解技术应用于循环谱密度矩阵从而进行循环频率检测的新方法。利用低秩稀疏分解出的带有循环平稳特征的稀疏矩阵构建检测函数对循环频率进行检测。仿真结果表明该方法在强噪声干扰下循环频率检测的优越性：在信噪比为-10 dB下仍精准可检测到前5阶循环频率。根据蒙特卡洛模拟得到ROC曲线可以为不同信噪比下检测不同阶数的循环频率提供参考。该方法也可进一步应用到滚动轴承的早期故障检测上，通过轴承加速疲劳寿命试验数据进行验证，试验结果表明：该方法在第2 297 min可以有效检测到轴承内圈故障，对比传统包络谱和谱峭度的方法有明显的优势。