预测金属有机骨架甲烷和氢气输送能力的迁移学习建模

陈少臣， 程 敏， 王诗慧， 吴金奎， 罗 磊， 薛小雨，吉 旭， 张长春， 周 利

（1. 四川大学化学工程学院, 成都 610065； 2. 四川铭泰顺硬质合金有限公司, 遂宁 629201）

当今世界面临严重的能源短缺和环境污染问题， 寻找、 开发可靠的清洁能源是解决这些问题的重要手段［1～3］. 甲烷与氢气燃烧时不产生有毒有害物质， 均为清洁能源， 受到广泛关注［4～6］. 然而， 甲烷与氢气目前主要使用制造成本高、 危险性大的高压容器进行储存， 限制了它们的大规模应用［7，8］. 于是，研究人员开始寻求低压条件下储存甲烷与氢气的方法. 金属有机骨架（MOFs）是一种结构高度可调、具有卓越的主客体相互作用的新型纳米多孔材料， 通常以金属和有机配体通过自组装形成［9］. 相比于沸石和活性炭， MOFs具有更强的气体吸附能力， 拥有巨大的潜力去实现甲烷与氢气的低压储存［4］. 此外， MOFs在物质分离［10，11］、 传感器［12］、 催化［13］和光捕捉［14］等领域也有巨大的应用前景.

MOFs吸附甲烷和氢气的研究经历了较长的发展历程. 最初， 当MOFs的种类还不多时， 研究人员直接通过实验合成来表征与改善MOFs对甲烷和氢气的吸附能力［15，16］. 如， 仲崇立等［17］以MOF材料PCN-14为基础， 采用质心分布图研究甲烷在PCN-14中的吸附机理， 设计出了具有更高甲烷吸附性能的MOF材料PCN-M； Furukawa等［18］设计合成了 MOF-180， MOF-200， MOF-205和MOF-210， 它们均具有优异的氢气吸附能力. 然而， Wilmer等［19］在2011年开发出的hMOFs假想结构数据库让MOFs的结构数量急剧增加， 使得实验法筛选MOFs变得成本高昂且效率低下. 随后， 基于分子模拟的高通量筛选技术成为了大规模筛选高性能MOFs的重要手段［20，21］. 如， Simon等［22］对hMOF数据库中的10000个MOFs进行了筛选， 以确定其甲烷储存性能的极限； Snurr等［23，24］先后在室温、 低温的储氢条件下对MOFs进行高通量筛选， 找到了具有高储氢性能的MOFs. 随着时间的推移， MOFs的数量在进一步扩大， 基于分子模拟的高通量筛选也逐渐变得耗时且昂贵.

得益于人工智能和大数据计算技术的高速发展， 研究人员开始利用机器学习（Machine learning，ML）技术建立预测模型， 快速评估MOFs对甲烷和氢气的输送能力， 降低筛选成本. 例如， Fernandez等［25］利用非线性支持向量机与10000个MOFs的甲烷吸附数据（298 K/100 bar， 1 bar=0.1 MPa）建立了高精确度的预测模型， 决定系数R2可达到0.93； Fanourgakis等［26］开发了一种原子类型描述符， 使用随机森林建立了MOFs在多种压力下吸附甲烷和二氧化碳的预测模型； Anderson等［27］使用18000个ToBaCCo-MOFs与深度神经网络， 在多种条件下建立了预测氢气吸附能力的模型； Bucior等［28］开发了一种能量描述符， 针对不同的MOFs数据库， 使用LASSO回归建立了氢气储存性能的预测模型. 但是， 受限于时间与经济成本， 研究人员往往无法获得足量的数据. 当数据量不足时， 传统方法所建立的ML模型的精确度与稳定性都会面临大幅度降低的风险， 使得模型的可信赖程度大打折扣. 严重时， 模型甚至会不再具有可用性. 此外， 传统方法所建立的ML模型也存在着通用性较低的问题， 无法快速适应新的预测任务. 因此， 利用少量数据建立高精确度、 高稳定性的预测模型成为一个更高的目标［29］.

迁移学习（Transfer learning， TL）是一种ML技术， 在只有少量新数据的情况下， 它可以利用从以往已有的大数据集中学习到的“知识”来帮助模型学习， 从而使模型在新的任务上具有良好的预测精确度［30，31］. 目前， TL已经应用于情感分类、 图像分类及机器翻译等领域. 在材料领域， TL建模方法也逐渐受到重视， 如， DeCost等［32］利用TL与深度卷积网络来学习微观结构的表示， 然后使用这些表示来推断潜在的退火条件； Wu等［33］利用TL模型预测了高分子的热导率； Yamada等［34］利用TL模型预测了聚合物和无机材料的多种性质； Colón等［35］利用TL模型预测了MOFs在多种吸附条件下的氢气吸附能力；Wang等［36］将晶体图卷积网络与TL进行结合， 预测了MOFs在低压条件下的甲烷吸附能力与吸附能量；Zhao等［37］使用TL模型预测了三组分超临界水混合物的扩散系数； Lim和Kim［38］使用TL模型预测了甲烷在MOFs中的自扩散系数.

本文利用少量数据与TL建立MOFs的甲烷、 氢气输送能力预测模型， 以克服当下传统ML模型训练需要大量数据的难题. 首先计算了12020个真实实验合成出的MOFs的6个几何描述符与甲烷、 氢气输送能力数据. 输送能力是一个评估MOFs吸附能力的关键指标， MOFs的气体输送能力等于MOFs补充气体时的最大吸附量减去MOFs需要补充气体时的吸附量. 此后， 利用TL方法建立预测模型， 只付出较小的代价， 就能快速、 精确地评估大量MOFs在不同输送条件下的甲烷、 氢气输送能力， 以应对不一致的、 变动的输送能力标准［39～41］. 进一步地， 通过对比不同TL模型的描述符重要度分布来明确“知识”的共享情况， 提高TL模型的可解释性. 最后， 展示了重要描述符与输送能力之间的结构-性能关系， 明确了重要描述符如何影响MOFs的甲烷、 氢气输送能力.

1 研究方法

1.1 数据集构建

使用Chung等［42］基于真实实验构建的CoRE-MOF数据库建立TL模型. 该数据集共包含12020个MOFs， 涉及到50多种金属簇和65种金属、 类金属原子， 其结构种类与化学性质非常多样.

为了对MOFs的抽象结构进行数字化， 计算了MOFs的6个常用的几何描述符， 包括最大空腔直径（Largest cavity diameter， LCD）、 孔隙极限直径（Pore limiting diameter， PLD）、 密度（Density）、 体积可达表面积（Accessible volumetric surface area， AVSA）、 质量可达表面积（Accessible mass surface area，AMSA）以及氦孔隙率（Void fractions， VF）. 前5个描述符以分子半径为1.86 Å（1 Å=0.1 nm）的氮气［43］作为探针， 使用Zeo++0.3［43］软件计算得到； 而VF则由分子半径为1.32 Å的氦气［44］作为探针， 通过RASPA 2.0［44］工具包计算得到.

基于RASPA工具包， 采用巨正则蒙特卡洛（Grand canonical Monte Carlo， GCMC）模拟甲烷和氢气在MOF中的吸附行为. 在所有的GCMC模拟中， MOF被视为刚性结构以缩短模拟时间， 甲烷、 氢气分子与MOF骨架之间的非键相互作用由Lennard-Jones（LJ）势表示， 并在球形距离12.8 Å处被截断. 用于GCMC模拟的单胞沿着三维方向至少扩展到25.6 Å， 并对其施加周期性边界条件. MOF中的原子和气体分子的LJ势能参数分别来自于UFF力场［45］和TraPPE力场［46］， 其参数列于表S1和表S2（见本文支持信息）. 每个MOF的GCMC模拟总共执行4000次循环， 前2000次用于系统初始化， 后2000次用于热力学性质平均. 图S1～图S3（见本文支持信息）表明更多的循环数几乎不会对模拟结果产生明显的影响，只会消耗更多计算资源. 每次模拟循环由n个Monte Carlo移动组成（n为吸附质分子的数量， Monte Carlo移动包括平移、 旋转、 再生和交换）.

基于吸附数据， 计算出MOFs对甲烷、 氢气的输送能力数据［47］， 计算公式如下：

式中：Nwc（mol/kg）代表MOFs对气体的输送能力， 下文以GCMC值代指Nwc的计算数值；Nads（mol/kg）代表MOFs补充气体时的最大吸附量；Ndes（mol/kg）代表MOFs需要补充气体时的吸附量. 本工作中计算的MOFs的甲烷和氢气输送能力数据集信息见表1， 其数据分布见图S4～图S6（见本文支持信息）. 在源任务上， MOFs的甲烷输送能力分布的全部范围与主要范围分别为0～65和0～10 mol/kg； 在任务T1上，MOFs的甲烷输送能力分布的全部范围与主要范围分别为0～120和0～20 mol/kg. 2015年， Fu等［48］对来自于hMOF数据库的hMOF-1162进行了GCMC模拟， 发现hMOF-1162在233 K/75 bar～358 K/5 bar条件下的甲烷输送能力为31.602 mol/kg， 其输送能力在数据集D1中的排名为前1.4%； 在任务T2上， MOFs的氢气输送能力分布的全部范围与主要范围分别为0～110和0～20 mol/kg. 2018年， Kapelewski等［49］合成了MOF-Ni2（m-dobdc）， 并发现其在198 K/100 bar～298 K/5 bar条件下的氢气输送能力为6.665 mol/kg， 在数据集D2中的排名为前31.5%. 在任务T1和任务T2中输送性能排名前100的MOFs的信息记录在表S3和S4（见本文支持信息）中.

Table 1 Delivery capacity data sets of MOFs

1.2 源任务模型训练

源任务（Source task， ST）模型是一个具有1个输入层、 2个隐层、 1个输出层的深度神经网络（Deep neural network， DNN）， 每层的神经元的个数分别为6， 250， 150和1［图1（A）］. 将数据集D0按照8414∶1202∶2404的比例切分成训练集、 验证集和测试集， 分别用于训练ST模型、 确定ST模型的超参数及测试ST模型的泛化能力. ST模型的训练超参数如下： 学习率设为0.00001， 以使训练过程稳定； 使用ReLU［50］作为激活函数； 采用Adam［51］优化器协助模型参数更新； 选用均方误差损失函数（Mean square error， MSE）作为损失函数， MSE的计算公式为

式中：ŷi和yi分别代表模型回归的预测值和真实值；n为数据总数目. 使用早停技术［52］训练ST模型以避免其产生过拟合， 即模型在验证集上的损失函数值连续10轮不再变化， 就停止模型的训练过程， ST模型一共训练了10000轮.

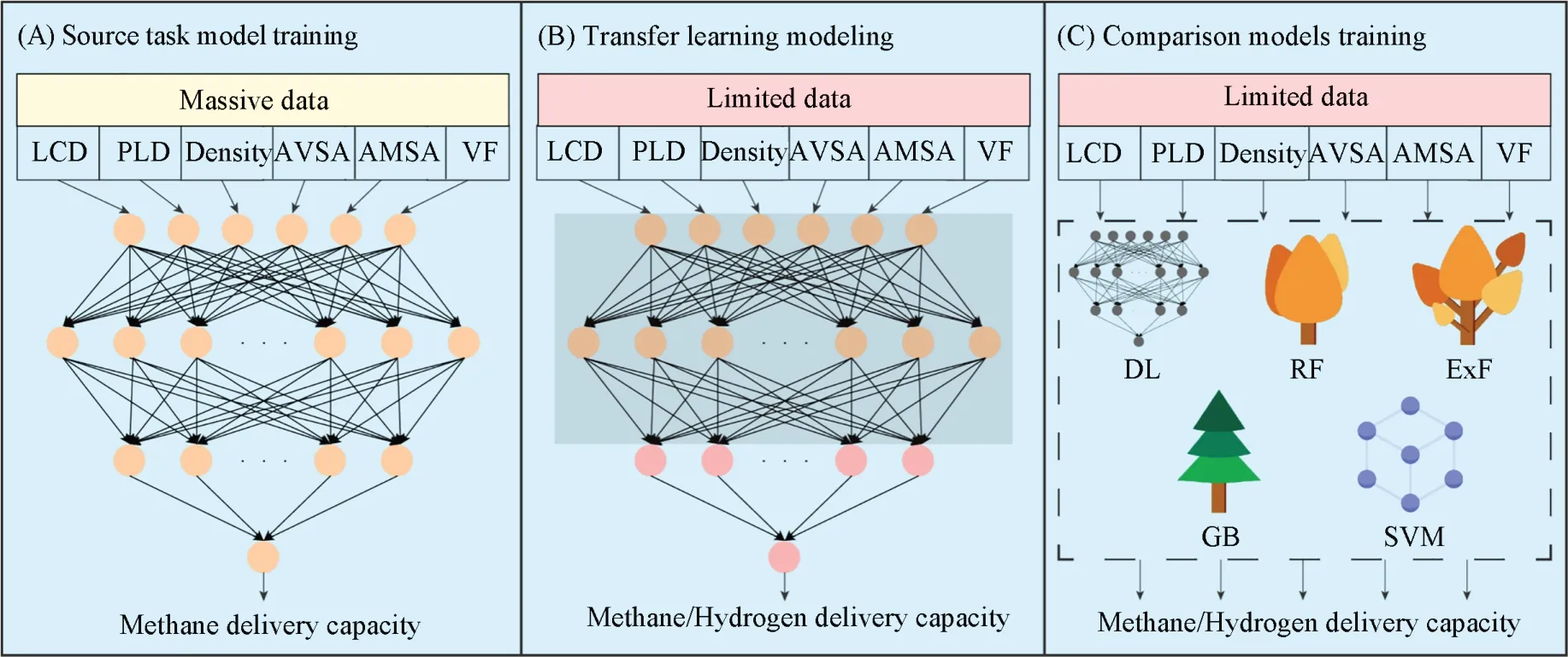
Fig.1 Main process of transfer learning modeling

1.3 迁移学习建模

基于ST模型， 分别使用MOFs在233 K/65 bar～358 K/5.8 bar条件下的甲烷输送量数据（数据集D1）和MOFs在198 K/100 bar～298 K/5 bar条件下的氢气输送量数据（数据集D2）进行TL建模， 这两个建模任务分别称为任务T1和任务T2. 采用基于参数的TL［30］进行建模， 具体方法如下： （1） 数据切分： 分别在数据集D1和D2中随机抽取无交集的训练集、 验证集、 测试集， 数据量为100∶100∶11820； （2） 参数冻结： 在微调ST模型之前， 预先固定ST模型的输入层至第二隐层之间的所有参数， 禁止其在微调ST模型时更新； （3） 模型微调： 分别使用步骤（1）中的训练集数据对ST模型进行训练， 训练过程即为微调［图1（B）］. 模型微调时的学习率、 激活函数、 优化器、 损失函数、 停止训练方法与1.2节保持一致， 两个TL模型分别训练了5000轮和4000轮.

1.4 模型对比与评估

采用与1.3节相同的数据集， 在任务T1和任务T2上分别训练5个传统的ML模型并与TL模型进行对比［图1（C）］， 这5个对比模型为： 与ST模型网络结构相同的直接学习模型（Direct learning， DL）、 随机森林（Random forest， RF）［53］、 极端树（Extra trees， ExT）［54］、 梯度提升树（Gradient boosting decision tree， GB）［55］及支持向量机（Support vector machine， SVM）［56］. 所有模型完成训练后， 使用相应的测试集对模型的预测精确度进行评价. 选取的评价指标为决定系数（R2）与MSE，R2的计算公式为

式中：ŷi为模型的预测值；yi为实际值；yˉ为所有yi的平均值.R2的取值范围为-∞～1， 越接近1代表模型预测精确度越高， 小于0代表模型的预测精确度还不如将所有的结果都猜测为yi的均值. 根据式（2）计算MSE， 其取值范围为0～+∞， 越接近于0代表模型的预测精确度越高. 由于MSE受到数据数值大小的影响， 所以只能在同一任务中比较模型的预测精确度， 不能比较不同任务中模型的预测精确度. 而R2则没有这种限制， 故下文主要采用R2来评价模型的预测精确度.

1.5 描述符重要度对比与结构-性能分析

为了明确TL模型具有良好预测精确度的原因， 基于预测模型与排列特征重要度［53］， 计算了源任务、 任务T1和任务T2中所有描述符的重要度， 并对比了描述符重要度的分布， 以明确TL取得成功的原因. 排列重要度的计算原理为： 首先， 将测试集送入模型中进行预测， 得到模型的评价指标Rmax. 此后， 依次将测试集中的第i个（本文中i≤6）描述符数据使用随机数替换， 以消除第i个描述符为模型预测所提供的信息， 最终得到6组新的测试数据. 将这6组新的数据依次送入模型中进行预测， 得到模型预测新数据集的评价指标定会小于Rmax， 于是对第i个描述符进行重要度的计算：

式中：Ii为在某个任务中， 第i个描述符的重要度，Ii越大， 意味着该描述符越重要. 在明确了每个任务中的重要描述符之后， 对重要描述符与输送能力进行结构-性能分析， 展示重要描述符变化时输送能力的变化趋势. 最后， 本文中所有程序均使用Python语言编写完成， ST， TL和DL模型均由开源深度学习框架Pytorch 1.7.0［57］实现， RF， ExT， GB和SVM均由开源机器学习框架Scikit-learn 0.23.2［58］实现.

2 结果与讨论

2.1 源任务模型的预测精确度

使用MOFs在298 K/65 bar～298 K/5.8 bar条件下输送甲烷的数据（数据集D0）训练ST模型. ST模型在测试集上的R2和MSE分别为0.973和0.372，具有很高的预测精确度. 图2给出了GCMC值与ST模型预测值之间的比较： GCMC值与预测值沿对角线紧密、 对称分布， ST模型为后面建立TL模型奠定了良好的基础.

2.2 迁移学习模型的预测精确度

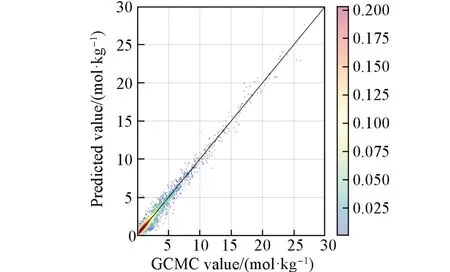
Fig.2 Density scatter plots for the GCMC valuepredicted value of ST model in source task

通过微调ST模型， 建立TL模型以适应任务T1和任务T2. 在进行TL建模之前， 先直接将任务T1和任务T2中的测试集送入ST模型中进行预测. 由于ST模型在训练时只使用了源任务中特定输送条件下的数据进行训练， 并未使用过新输送条件下的数据， 故ST模型在两个测试集上的R2分别仅为0.557和0.357， 无法适应新的预测任务. 如图3（A）和（B）所示， 两个任务中的GCMC值与预测值的分布都较大地偏离了对角线. 虽然ST模型在任务T1和任务T2上的预测精确度不高， 但是能够预测数据的大致趋势， 存在一定的潜力去建立TL模型.

Fig.3 Density scatter plots of GCMC value-predicted value of ST model in two tasks

此后， 对任务T1和任务T2进行TL建模. 在两个任务的测试集上， TL模型的R2分别为0.968和0.945， GCMC值与TL模型预测值都紧密分布在对角线上［图4（A）和（B）］， 表明TL模型具有精准的预测能力. 在任务T1和任务T2上， TL模型的预测精确性显著优于ST模型， 原因在于TL模型使用过新任务中的数据， 利用这些数据来调整模型中的部分参数以适应新的任务， 使TL模型在新任务上的预测精确性好于没有进行参数调整的ST模型. 此外， ST模型由MOFs的甲烷输送能力数据训练而来， 而任务T1和任务T2中的数据分别是其它输送条件下的甲烷、 氢气输送能力数据， 使得任务T1与源任务之间的相似性多于任务T2与源任务之间的相似性. 所以， 在任务T1上微调出的TL模型的预测精确度要高于在任务T2上微调出的TL模型的预测精确度.

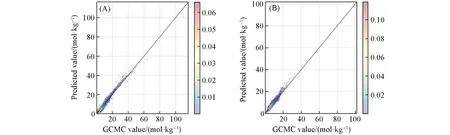
Fig.4 Density scatter plots of GCMC value-predicted value of TL model in two tasks

之后， 训练DL， RF， ExF， GB和SVM这5种传统的ML模型来进一步体现TL模型的竞争力. 表2中记录了所有模型在任务T1和任务T2上的R2， MSE记录在表S5（见本文支持信息）中. 在两个任务中， TL模型的R2全部高于5个ML模型， 拥有最高的预测精确度. 此外， DL模型的R2分别为0.926和0.912， 仅次于TL模型， 证明TL和DL模型所基于的DNN模型结构非常强大， 即使是DL模型都有一定的竞争力.

最后， 将任务T1和任务T2中输送性能最高的100个MOFs（TOP-100 MOFs）的数据送入各个模型进行预测， 比较不同模型预测TOP-100 MOFs的精确度是否有较大差异. 所有模型的R2和MSE分别记录在表3和表S6（见本文支持信息）中. 在任务T1和任务T2上， TL模型的R2分别为0.984和0.964， 仍然具有最高的预测精确度； DL模型的R2分别为0.962和0.914， 仍然仅次于TL模型； 而其它4个ML模型的R2仍然在0.9以下. 可见， TL模型在预测高输送性能MOFs的输送能力时， 依然能够保持高的精确度.

Table 2 R2 of different models in two tasks

Table 3 R2 of different models in two tasks with TOP-100 MOFs

2.3 迁移学习模型预测少量数据的稳定性

由于计算大量MOFs的描述符也需要花费较高的计算成本， 为了降低计算成本， 需要只关注少量或者部分MOFs的甲烷和氢气输送能力， 而不是关注整个数据库中的MOFs. 这时， 需要在关注模型预测精确度的基础上进一步关注模型的稳定性， 防止模型产生误差很大的预测结果.

为了验证模型预测少量数据时的稳定性， 选取了预测大量数据时预测精确度排名前二的TL和DL模型进行对比. 此外， 由于在现实应用中无法提前预知MOFs的甲烷、 氢气输送能力的高低， 所以在两个任务的测试集上（两个测试集与1.2节保持一致）随机抽取100个数据组成Batch， 送入TL和DL模型中进行预测以体现随机性， 进行1000次的随机抽取使结果具有统计学意义. 下文中和分别代表TL模型和DL模型在每个Batch上的预测精确度. 如图5所示， 两个任务中TL模型的的平均值分别为0.964和0.946； DL模型的的平均值分别为0.916和0.913. 在任务T1上， 有395个Batch的大于0.05， 有89个Batch的大于0.1； 在任务T2上， 有171个Batch的大于0.05， 有55个Batch的大于0.1. 这初步说明了TL模型预测少量数据时具有较高的稳定性，可以避免产生不确定的预测结果.

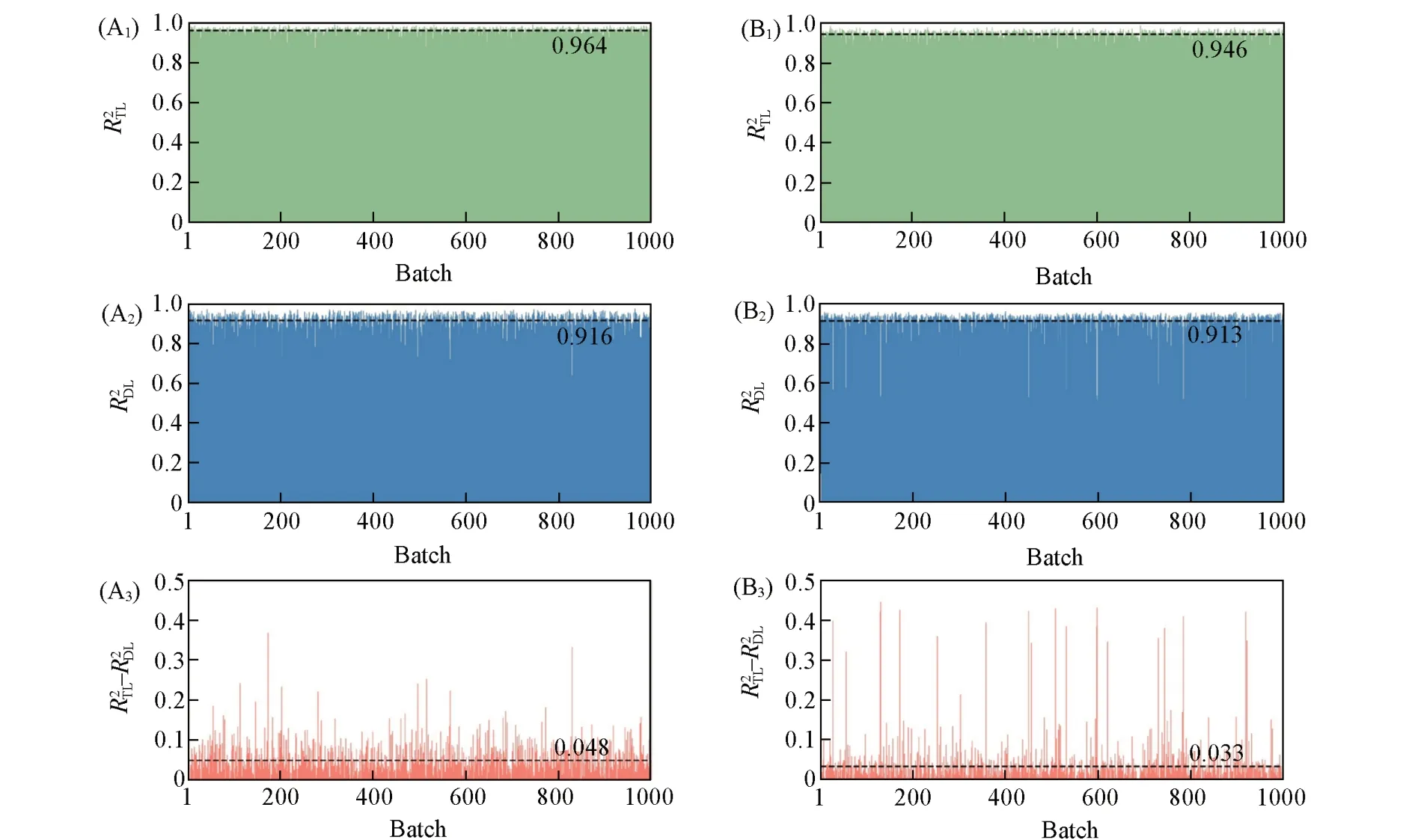
Fig.5 R2 of TL model and DL model in predicting a small amount of data in two tasks

进一步观察了所有Batch的R2分布情况. 在任务T1上， TL模型和DL模型的R2范围分别为0.875≤和［图6（A）和（B）］； 在任务T2上， TL模型和DL模型的R2范围分别为和［图6（C）和（D）］. 在这两个任务中，比分布范围更窄、 更加集中， 最差的也大于0.85； 而最差的仅大于0.5， 是一个很不确定的预测结果. 此外， TL模型的MSE的平均值、 最小值及最大值都小于DL模型（表S7， 见本文支持信息）. 可见， TL模型比DL模型具有更高的稳定性， 能够避免产生不确定的预测结果.

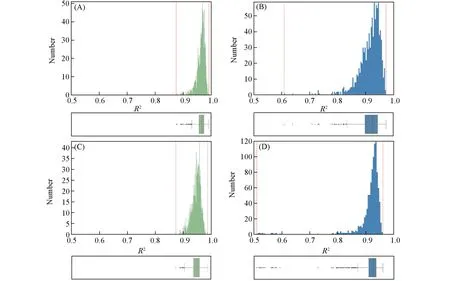
Fig.6 R2 distribution of TL model and DL model on 1000 small data sets in two tasks

2.4 描述符重要度对比与结构-性能分析

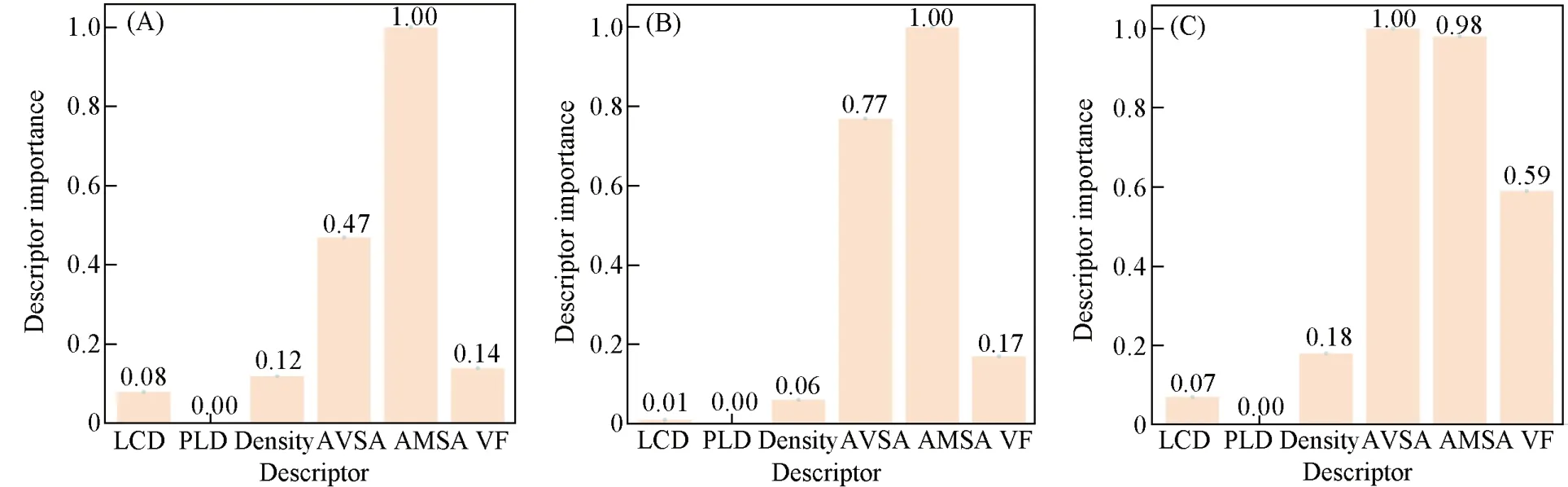
Fig.7 Distribution of descriptor importance of three tasks

为了明确TL模型在两个任务上取得良好效果的原因， 计算了ST模型和两个TL模型的描述符重要度， 对比3个模型之间的描述符重要度分布情况.

如图7所示， 对于ST模型和任务T1上的TL模型［图7（A）和（B）］， 由于二者都是预测甲烷的输送能力， 所以它们的描述符重要度分布相似度极高； 对于ST模型和任务T2上的TL模型［图7（A）和（C）］， 由于该TL模型预测的是氢气的输送能力， 所以两个模型之间的描述符重要度分布具有一定的差距， 但依旧是AMSA和AVSA这两个描述符最为重要. 总的来看， 对于这3个模型， 最重要的3个描述符都是AMSA， AVSA和VF， ST模型与TL模型之间有充分的共享“知识”， 使TL建模能够取得成功. 在此之前， Pardakhti等［7］和Wu等［59］分别通过随机森林和梯度提升树建立MOFs的甲烷吸附能力预测模型， 发现影响甲烷吸附的重要因素包括AMSA， AVSA和VF； Konstas等［15］和Suh等［16］报道了在实验中可以通过改变MOFs的表面积来增强其吸附甲烷和氢气的能力； Anderson等［60］更是证明了DNN可以很好地预测MOFs对小的、 近似球形的、 非极性的单原子或双原子分子的吸附能力， 这意味着基于DNN实现的TL模型是可信赖的.

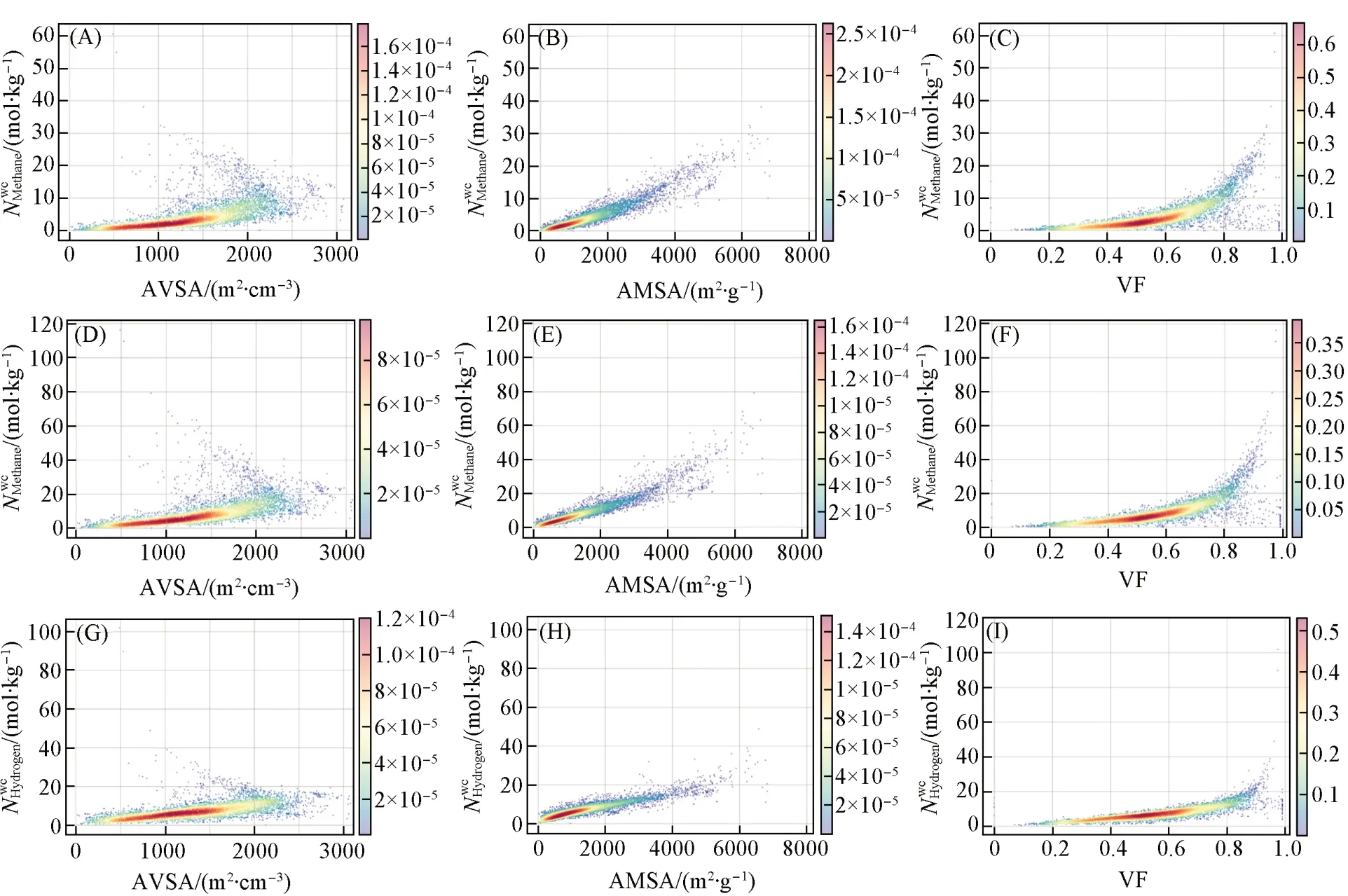
Fig.8 Density scatter plots of important descriptors-delivery capacity in three tasks

在此基础上， 分析MOFs的结构-性能关系， 展示重要描述符变化时输送能力的变化趋势. 如图8（A），（ D）和（G）所示， AVSA增大会对大部分性能一般的MOFs的甲烷和氢气输送能力起到提升作用， 主要呈现正比例关系. 当AVSA从0增大到3000 m2/cm3时， MOFs的甲烷和氢气输送能力会不断增大. 然而， 对于输送能力较高的MOFs， AVSA会对MOFs的输送能力起到抑制作用， 呈现反比例关系，AVSA从500 m2/cm3增大到2000 m2/cm3， MOFs的甲烷和氢气输送能力会越来越小， 最终减小为约20 mol/kg. AMSA对MOFs的甲烷和氢气输送能力都起到了提升作用， 大致呈现正比例关系. 当MOFs输送甲烷时［图8（B）和（E）］， AMSA从0增大到4000 m2/g时， MOFs的甲烷输送能力会较均匀地增大；但是当AMSA＞4000 m2/g时， MOFs的甲烷输送能力会快速增大. 当MOFs输送氢气时［图8（H）］， AMSA从0增大到4000 m2/g时， MOFs的氢气输送能力的增加速度会越来越慢； 但是当AMSA＞4000 m2/g时，MOFs的氢气输送能力又开始快速增大. VF同样对MOFs的甲烷和氢气输送能力起都到了提升作用.当MOFs输送甲烷时［图8（C）和（F）］， VF从0增大到0.6， MOFs的甲烷输送能力会较均匀且缓慢地增大到10 mol/kg左右， 提升效果并不很明显； 当VF＞0.6后， MOFs的甲烷输送能力会随着VF的增大而快速增大， 提升效果变化显著. 当MOFs输送氢气时［图8（I）］， VF增大到0.8以后， 输送效果才快速增大. 最后， 对于LCD， PLD和Density这3个重要度较低的描述符， 它们与输送性能的关系图见图S7（见本文支持信息）. 在3个任务中， LCD和PLD与输送性能呈现不太强烈的正比例关系， 高输送性能的MOFs有较大的LCD和PLD. 而Density与输送性能则呈反比例关系， Density从0增大到1 g/cm3时，MOFs的甲烷和氢气输送性能会急速下降到20 kg/mol以内， 降低MOFs的Density有利于MOFs的甲烷、氢气输送性能的提升.

3 结 论

寻找甲烷和氢气这两种危险的燃料气体的安全高效输送方法是推动其大规模应用的核心任务之一. MOFs是一种具有优良气体吸附能力的新型纳米多孔材料， 具有实现气体低压输送， 进而使甲烷和氢气得到大规模应用的潜力. 本文提出了一种数据需求量小的基于DNN的TL建模方法， 通过冻结ST模型的部分参数， 使用其它输送条件下的甲烷、 氢气输送数据， 对ST模型进行微调以得到TL模型， 使TL模型在新的任务下具备精确、 稳定的预测性能. 从而可以快速应对多种不同的甲烷、 氢气输送标准， 大量节约模拟计算成本. 与传统的ML模型相比， TL模型具有最好的预测精确度， 当预测少量数据时， TL模型也能够保持稳定性， 不会产生坏的预测结果. TL模型在不同预测任务上取得良好预测效果的原因是ST模型与TL模型之间存在较多的共享“知识”， TL模型能够捕捉到正确、 符合理论实际的结构-性能关系. 为了使模型具备更高的通用性， 本文只选用了常见的几何描述符. 除MOFs外， 如共价有机骨架、 多孔聚合物网络和沸石咪唑酯骨架等新型纳米多孔材料都具有这些几何描述符. 随着时间的推移， 其它新型纳米多孔材料的种类也在快速增长. 本文所使用的TL建模方法不仅限于研究实验合成出的MOFs， 还可以推广到多种新型纳米多孔材料的研究上.

支持信息见http: //www.cjcu.jlu.edu.cn/CN/10.7503/20220459.