某多孔弹性场地地面爆炸声传播特性和当量反演分析

张亮永，卢 强，梁旭斌，李鹏毅，方厚林，曾新吾

某多孔弹性场地地面爆炸声传播特性和当量反演分析

张亮永1, 2，卢 强2，梁旭斌2，李鹏毅2，方厚林2，曾新吾1

(1. 国防科技大学气象海洋学院，长沙 410073；2. 西北核技术研究所，西安 710024)

准确预测地面爆炸威力对生产生活安全和武器性能测试具有重要意义．为获取雪和半灌木混合覆盖地表场地的地面爆炸声传播特性，解决该场地地面爆炸当量反演问题，在实测数据基础上分析了该场地的声传播特性，之后采用有限边界阻抗声传播理论和四参量阻抗模型建立该场地声传播模型并进行讨论．最后，基于以上声传播模型，建立了多孔场地地面爆炸当量估计的折合声冲量法(简称多孔场地折合声冲量法)和以多孔场地折合声冲量法为声学模型的声震分析方法，对该多孔场地地面爆炸当量进行了反演和分析．结果表明，雪和半灌木覆盖地表场地的地面爆炸声信号能量集中在低频(20Hz以内)，受到多孔地表和空气吸收影响，超压幅值随距离增加快速衰减，其衰减系数1.25明显大于球面波几何扩展系数1．基于有限边界阻抗波传播理论和四参量阻抗模型建立的声传播模型可以准确描述该多孔场地波传播特性，其预测波形和实测波形基本重合．基于以上声传播模型建立的多孔场地折合声冲量法，通过考虑声震能量分配过程可以获得较高的当量反演精度，当量相对误差不超过7%．而采用折合声冲量法并联合地震波数据进行声震分析，可以准确获取多孔弹性地面附近未知爆炸事件的当量和爆高，当量和爆高相对误差分别不超过7%和19%．

地面爆炸；有限边界阻抗；四参量模型；折合声冲量；声震分析

工业爆炸事故[1]和恐怖袭击事件[2]涉及生产生活安全，通常发生在地表附近，属于典型的地面爆炸事件，对其爆炸威力监测有助于毁伤快速评估和迅速救援．战斗部打击地面目标[3]也属于典型的地面爆炸事件，在靶场试验中进行爆炸威力监测有助于武器性能评估和未爆弹排除．因此，准确预测地面爆炸威力对生产生活安全[1-2]和武器性能测试[3]具有重要意义．由于地面爆炸能量会耦合到空气中，并产生明显声扰动，一般通过远场声学数据利用超压峰值、正向声冲量和正向脉宽等波形特征量来预测地面爆炸当量[4-12]．为建立波形特征量和爆炸当量之间关系，相继提出ANSI模型[6,13]、KG85标准模型[14]、BOOM模型[6,15]、IPM声学模型[10]、地面爆炸声学模型[2]和近地面爆炸声学模型[9,16-17]等经验或半经验模型，以及超压波形匹配法、经验声源模型法等全波形当量反演方法[5,7,11,17]．Kim等[5]基于线性声学理论反演爆源等效源时间函数，以KG85模型折合声冲量作为参考函数，提出一种地面爆炸当量反演新思路(本文称为折合声冲量法)，并将其应用在刚性地面爆炸当量反演上，具有较高的当量预测精度．

但上述方法没有考虑波传播过程中地表结构的影响，只是简单地将地面假设为刚性界面，而基于声学数据预测地面爆炸当量的精度和地表结构以及介质特性密切相关，地面爆炸耦合到空气中的超压波形受到声震能量分配[16-21]以及地表反射、散射和吸收的共同作用[22-29]，使得声衰减特性和波形特征随地表结构和介质不同产生明显差异．对于声衰减特性，混泥土等硬地表对声接近全反射[22]，但多孔弹性地表如覆盖地面的雪、草等吸收作用明显[22,25,30]，波的衰减系数明显大于1．对于波形特征，入射波经多孔弹性地表反射后波形会产生明显变化，变化情况和覆盖层阻抗密切相关[23,25,27-33]．研究表明[23,27,31]，地表覆盖层为雪时，地面附近存在声表面波，频域上低频部分得到增强，高频部分由于雪层吸收快速衰减，时域上超压峰值降低，波形脉宽更宽．

文献[23，28，34-37]建立了有限边界阻抗声传播理论，从理论上解决复杂地面结构波传播问题．文献[38-42]建立单参量、四参量和JCAL等地表阻抗模型，用于地表附近声传播特性分析．而文献[25，27，29-31]应用以上理论和模型对雪、草等单一多孔介质地表波传播问题进行了研究，建立了单一多孔介质波传播问题的基本思路．

为了获取雪和半灌木混合覆盖地表场地的地面爆炸声传播特性，解决该场地地面爆炸当量反演问题，本文首先基于实测数据分析该场地声传播特性，之后采用有限边界阻抗波传播理论和四参量地表阻抗模型建立该多孔场地声传播模型并进行讨论．最后，基于以上声传播模型建立多孔场地折合声冲量法和以多孔场地折合声冲量法为声学模型的声震分析方法，并采用以上方法对该场地地面爆炸当量反演精度进行讨论．

1 某多孔弹性场地地面爆炸试验

基于地面爆炸声测点数据对雪和半灌木混合覆盖地表场地的声传播特性进行分析．

1.1 场地情况和测点分布

场地介质为含砂砾的冻土，表面由积雪覆盖，夹杂半灌木稀疏分布，如图1所示．爆源放置地面，爆高为0.16m，当量为30kg，传感器对准爆心依次排开(见图2)，根据测点距离选用不同类型传感器(见表1)．声测点距离爆心最远3km，在该距离内地势相对平坦，基本无风，环境参数见表2．

图1 场地环境

表1 传感器参数

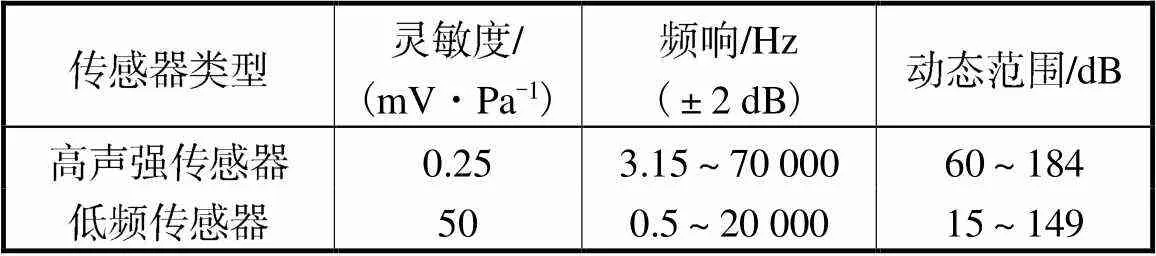
Tab.1 Transducer parameters

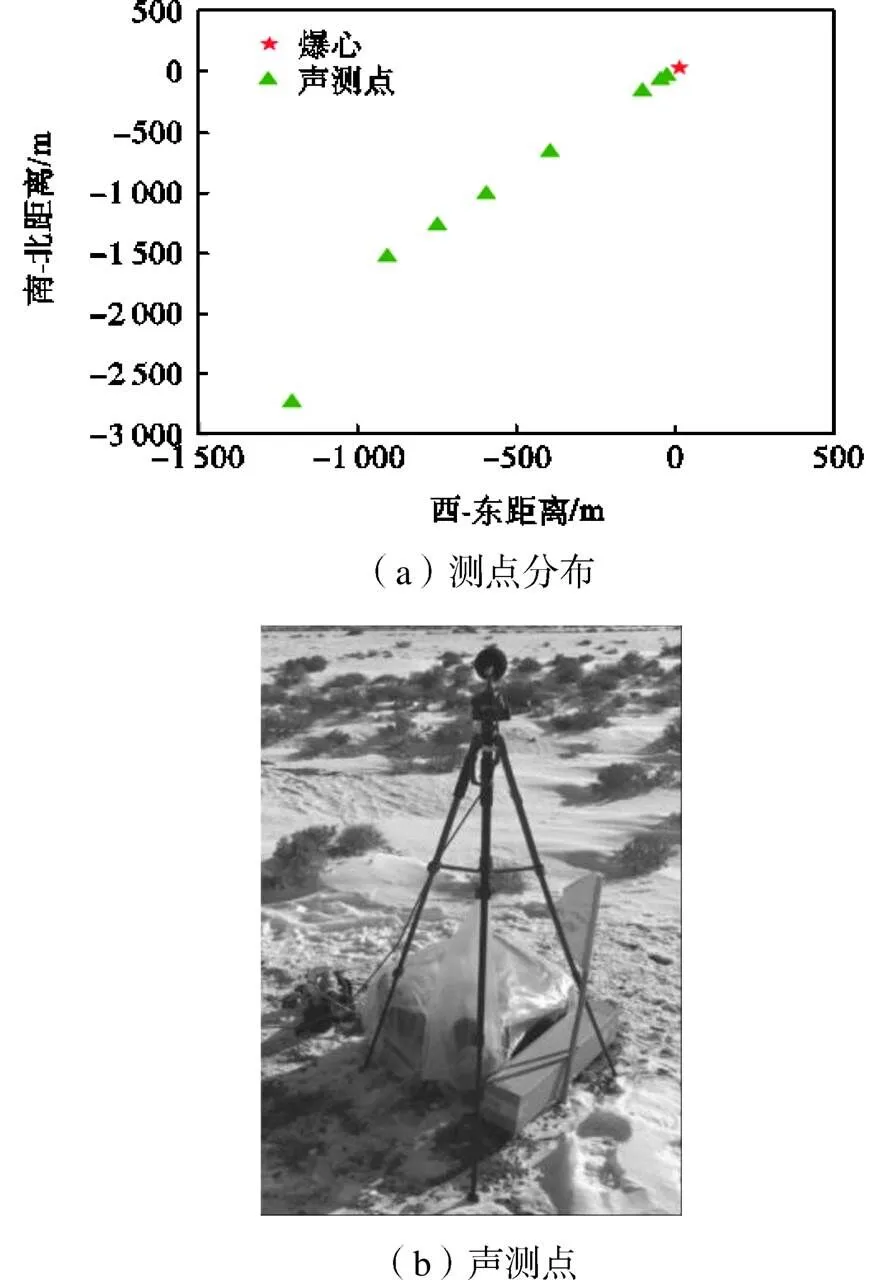
图2 测点分布

表2 大气环境参数

Tab.2 Environment parameters of the atmosphere

1.2 实测数据

地面爆炸耦合到空气中的超压波形(见图3)，随着传播距离增加，其幅值、脉宽等波形特征发生明显变化．测点爆心距见表3，地面爆炸最近测点S01的爆心距为80m，30kg当量对应比距离为25.7m/kg1/3.研究表明[5,14]，比距离大于20m/kg1/3时波传播满足线性声学变化规律，可以采用线性声学理论进行传播特性分析．

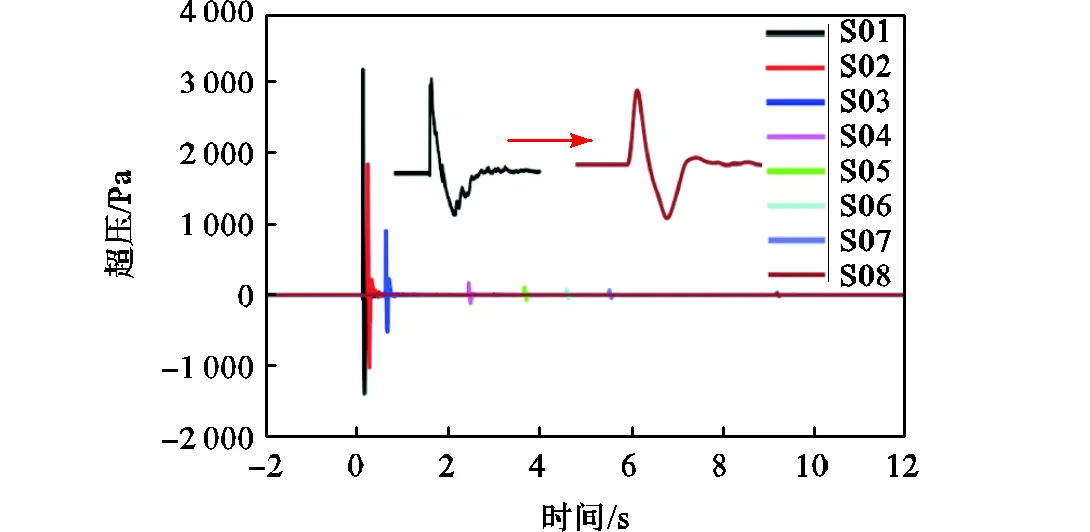
图3 声测点时域波形

图4中红色圆点为超压幅值实测数据，红色曲线为实测数据最小二乘拟合曲线，黑色曲线为30kg当量的KG85超压峰值模型衰减曲线，其中拟合曲线计算式为

表3 测点距离

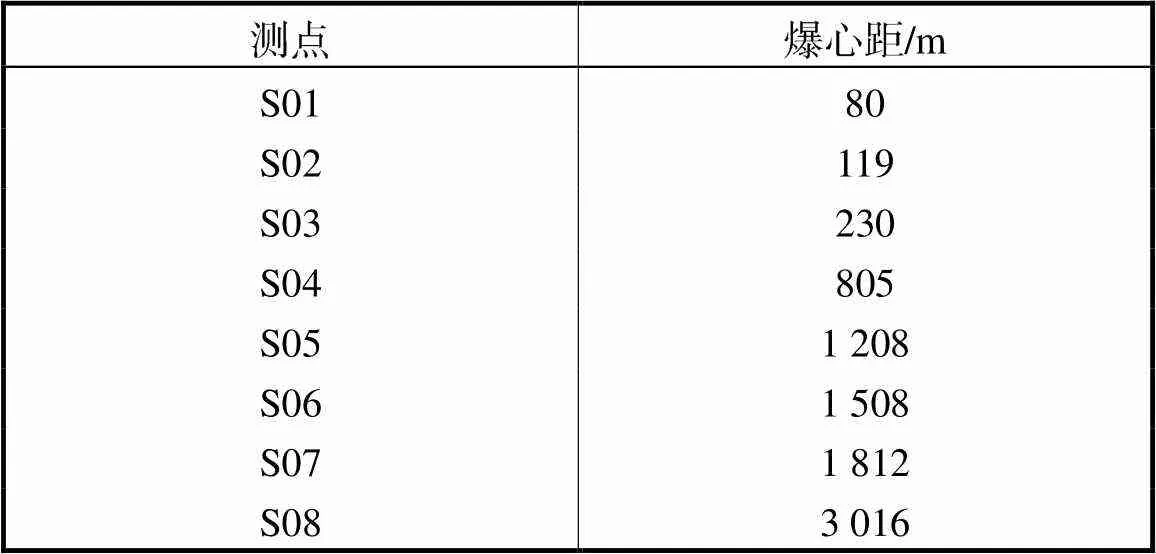
Tab.3 Measuring point distances

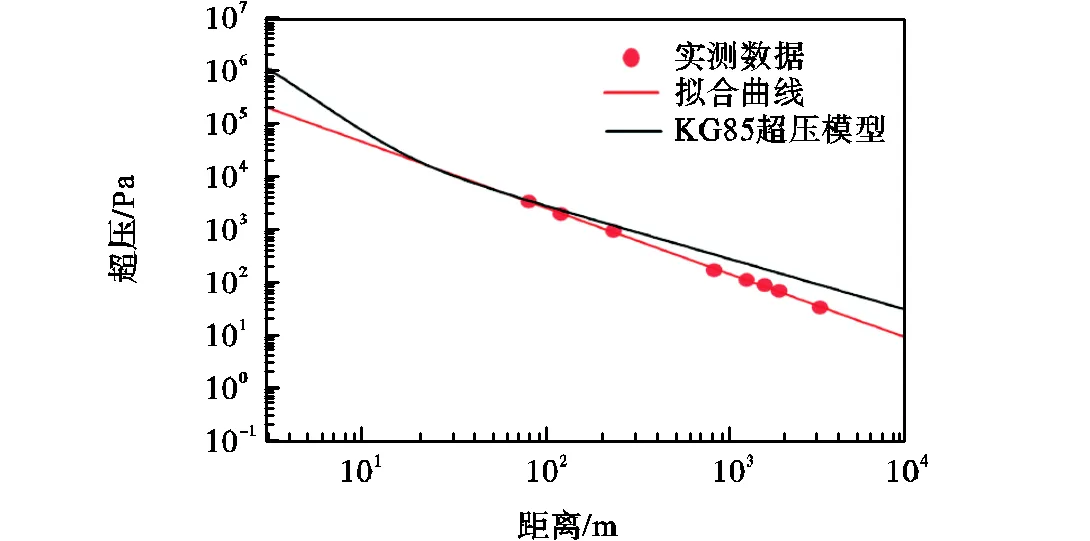
图4 声测点超压幅值衰减规律

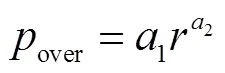
式中：1和2为待定系数，拟合值分别为7.70×105和－1.25；over为超压峰值，Pa；为距离，m. KG85超压峰值曲线计算式[14]为

(2)

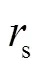
由地面爆源各测点数据的主频和归一化频谱可知(见图5和图6)，信号主频位于9～14Hz之间，大于主频之后信号能量快速衰减，整个信号能量集中在20Hz以内(－3dB对应的最大频率)．由图6可知，主频之后的信号能量衰减存在一个拐点频率，在这个拐点频率之后测点频谱受到噪声干扰影响发生复杂变化，且拐点频率和测点距离有关，远距离测点S08的拐点频率最小，为80Hz．对比图6中各测点的归一化频谱可知，大于主频的归一化幅值随测点距离增大具有变小趋势，而小于主频的归一化幅值随测点距离增大分为两个阶段，即近距离(230m内，S01～S03测点)减小阶段和远距离(超过230m，S03～S08测点)增加阶段．在远距离(超过230m)范围，大于主频的归一化幅值随测点距离增大具有变小趋势，小于主频的归一化幅值随测点距离增大具有变大趋势，表明远距离波传播过程中高频(大于主频部分)比重越来越小，低频(小于主频部分)比重越来越大．以上表明，声传播过程中声信号以低频(20Hz以内)为主，受到多孔地表和空气吸收的影响，波在远距离传播过程中低频(小于主频)衰减较慢，高频(大于主频)衰减较快，使得波的衰减系数高于理想球面波几何扩展系数．

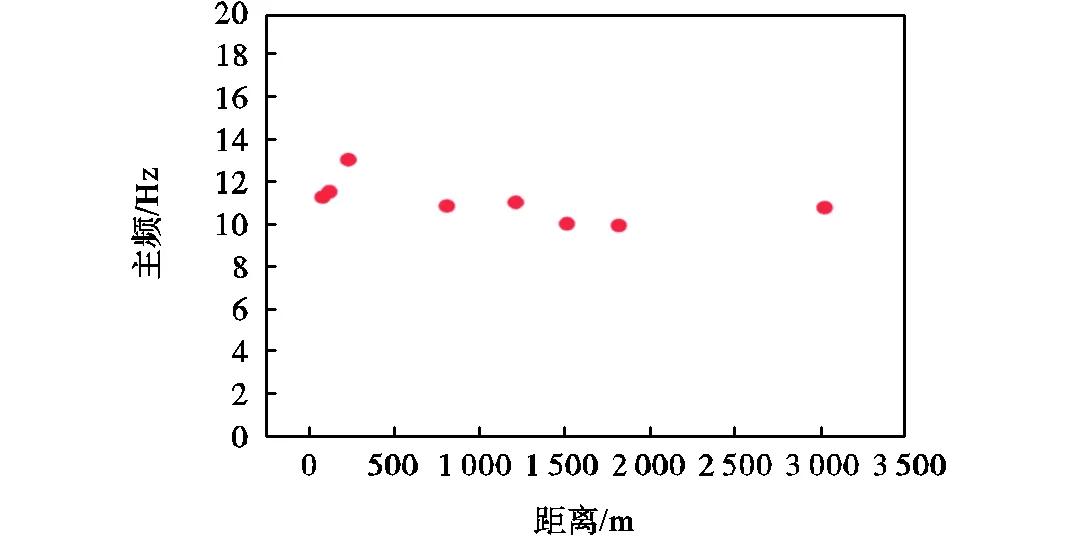
图5 声测点的主频

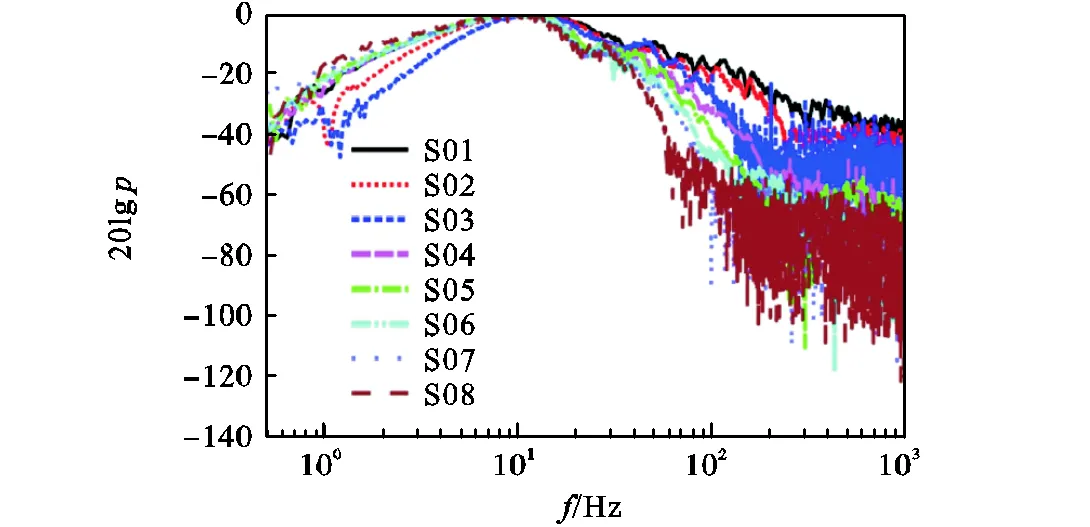
图6 声测点的归一化频谱

2 某多孔弹性场地声传播模型

基于有限边界阻抗声传播理论和四参量阻抗模型，并结合雪和半灌木混合覆盖地表场地的介质参数，建立该多孔场地声传播模型并进行讨论．

2.1 理 论

2.1.1 有限边界阻抗声传播理论

建立3层介质模型，分别为空气层、多孔弹性覆盖层和无孔弹性垫层，见图7．忽略时间项，基于球面波理论的自由场速度势函数[30,36]为

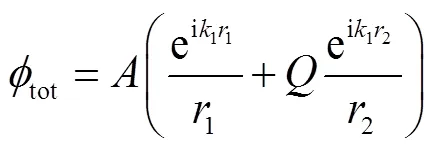
式中：A为常数部分；为直达波距离；为反射波距离；k1为空气中波数；Q为无量纲虚拟源强度项．

Albert等[30]和Attenborough[36]给出了的理论解，即

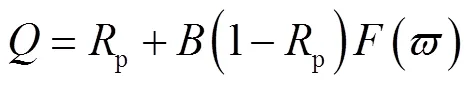
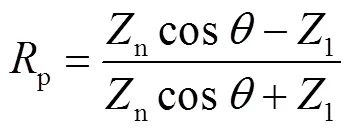
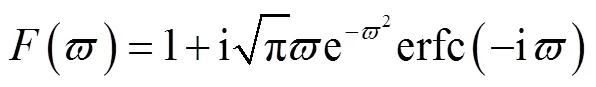
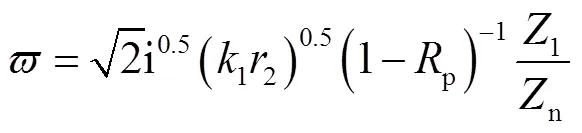
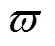
根据速度势函数和声压关系[44]

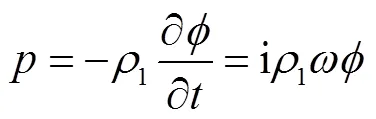
可得

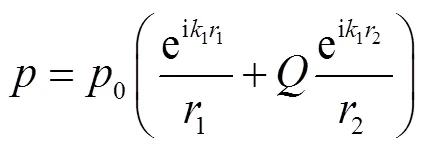
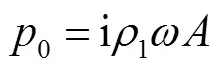
式中：0表征源特性；为角频率；为速度势．由于空气吸收作用也会造成声衰减[22,30,45-46]，将空气中声衰减系数[46]代入式(9)，得到

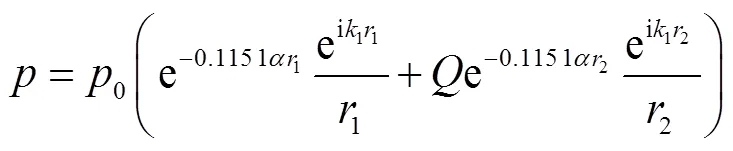
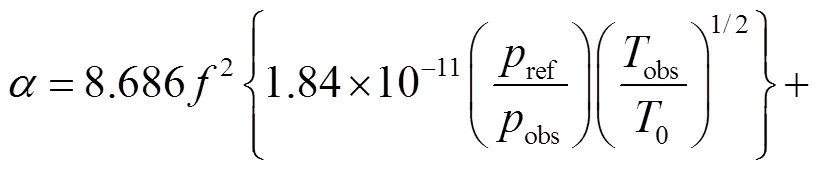
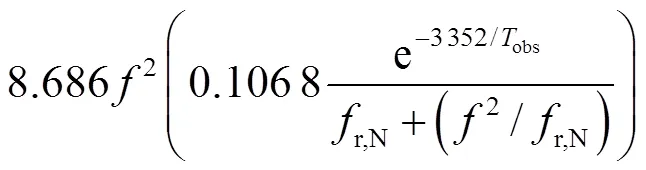
式中：为大气衰减系数，dB/m；r,O和r,N分别为氧和氮的振动弛豫频率，

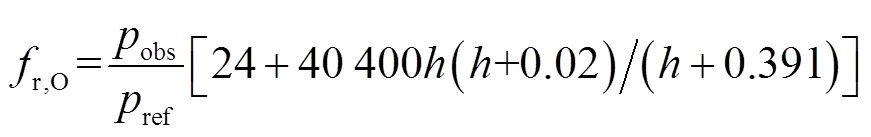
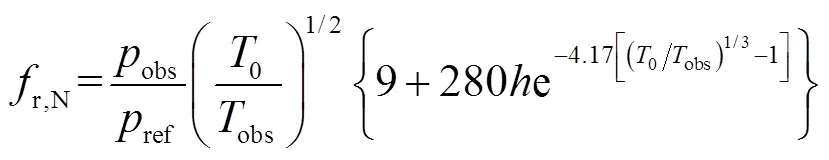
式中：为水蒸气克分子浓度，%；为频率，Hz；obs为现场环境大气压，Pa；obs为现场环境温度，K；0为大气温度，K．由式(12)可知，空气衰减系数与频率平方近似成正比，频率越高衰减越快．

当测点爆心距远大于爆源和测点的高度之和时，式(11)可简化为

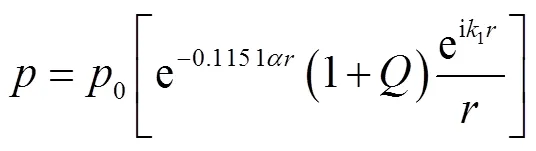
2.1.2 地表阻抗模型

对于两层地介质构成的地表模型(见图7)，其等效法向声阻抗率[39, 44]为

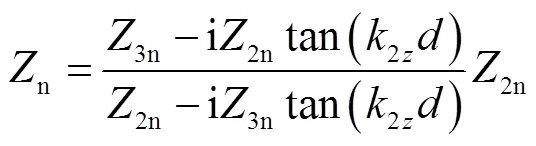
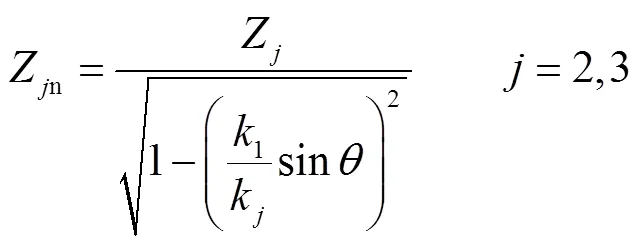
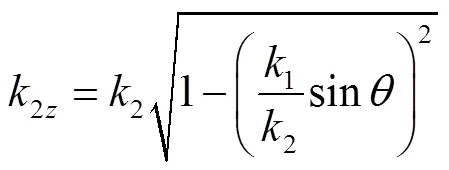
式中：Z和Zn分别为各层介质的声阻抗率和法向声阻抗率；k和k分别为各层介质波数和法向波数；为第1层地介质层厚，m．

Attenborough等[23,39]提出用流阻、孔隙率、颗粒形状因子′和孔隙形状因子比f等4个参量表征介质特性，建立了四参量模型，并在草、雪等多孔地表介质上得到应用[25,27,30-31]．Attenborough四参量模型[23,39]为

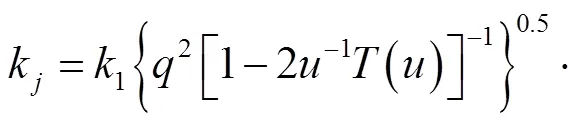
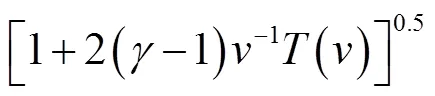
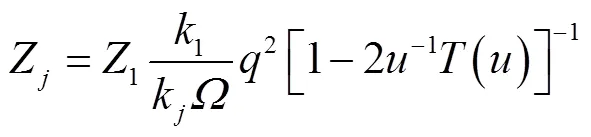
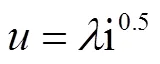
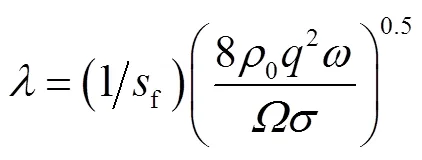
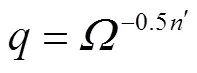
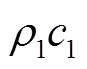
2.2 讨 论

空气声速和密度分别为330m/s和1.03kg/m3，雪的平均厚度为0.15m．由于多孔覆盖层以雪为主，覆盖层颗粒形状因子、孔隙率、孔隙形状因子参照雪取值[25,29,31]，见表4．为考虑半灌木影响，流阻通过波形匹配误差最小[31]计算得到，结果见图8．弹性垫层参照冻土参数取值[25,29,31]，见表4．

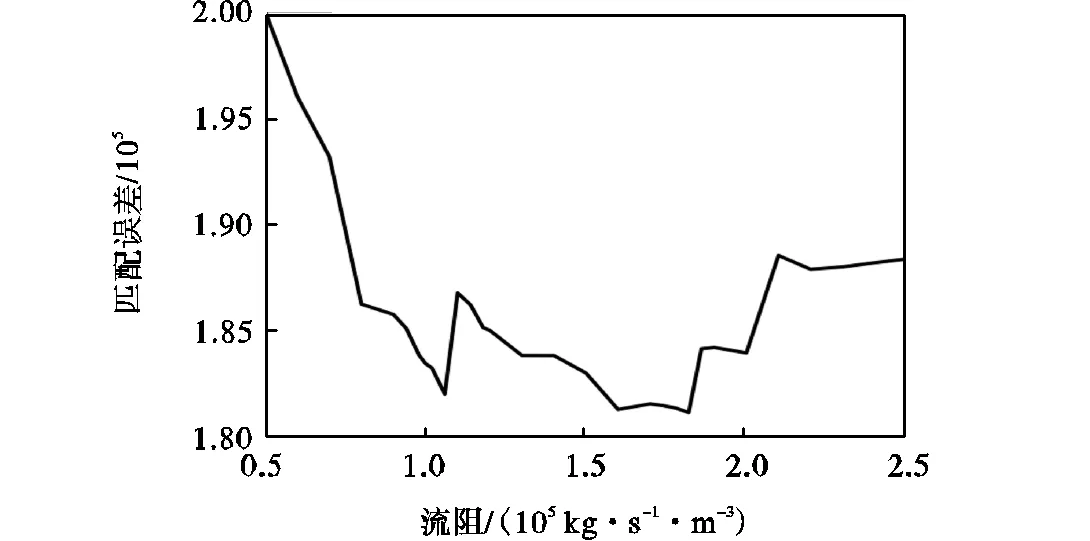
图8 计算波形和实测波形的匹配误差

表4 地表介质参数

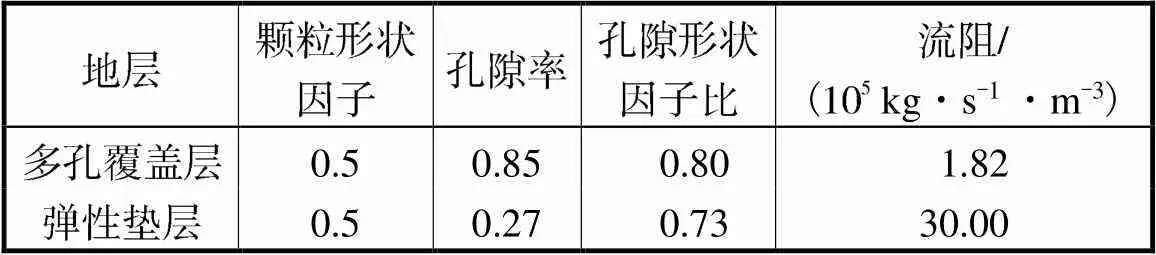
Tab.4 Surface medium parameters

将以上参数代入虚拟源强度项计算公式，得到不同距离测点的虚拟源强度项频谱(见图9)．由图可知，虚拟源强度项的幅值在低频部分存在峰值，主频和峰值大小与测点距离密切相关，随着测点距离增加低频部分得到增强，整体上呈现主频随距离增加变小、峰值随距离增加变大的趋势．此外，虚拟源强度项的相位随频率变化迅速增加后趋于不变，呈现S函数特征，而随测点距离增加相位变化更加陡峭，相位变化的拐点频率随距离增加呈现减小趋势，拐点频率之后相位随频率基本保持不变．

由虚拟源强度项和S01测点超压波形预测其余测点超压波形，结果见图10．图10中红色长虚线为实测波形，黑色实线为基于有限阻抗边界的预测波形，蓝色短虚线为只考虑空气声吸收和几何扩展的预测波形．由图可知，基于有限阻抗边界的预测波形和实测数据重合较好，而刚性边界预测波形和实测数据差别明显，表明边界阻抗对声传播特性影响显著，而采用有限边界阻抗波传播理论和四参量阻抗模型可以准确预测雪和半灌木混合覆盖地表场地的波传播特性．

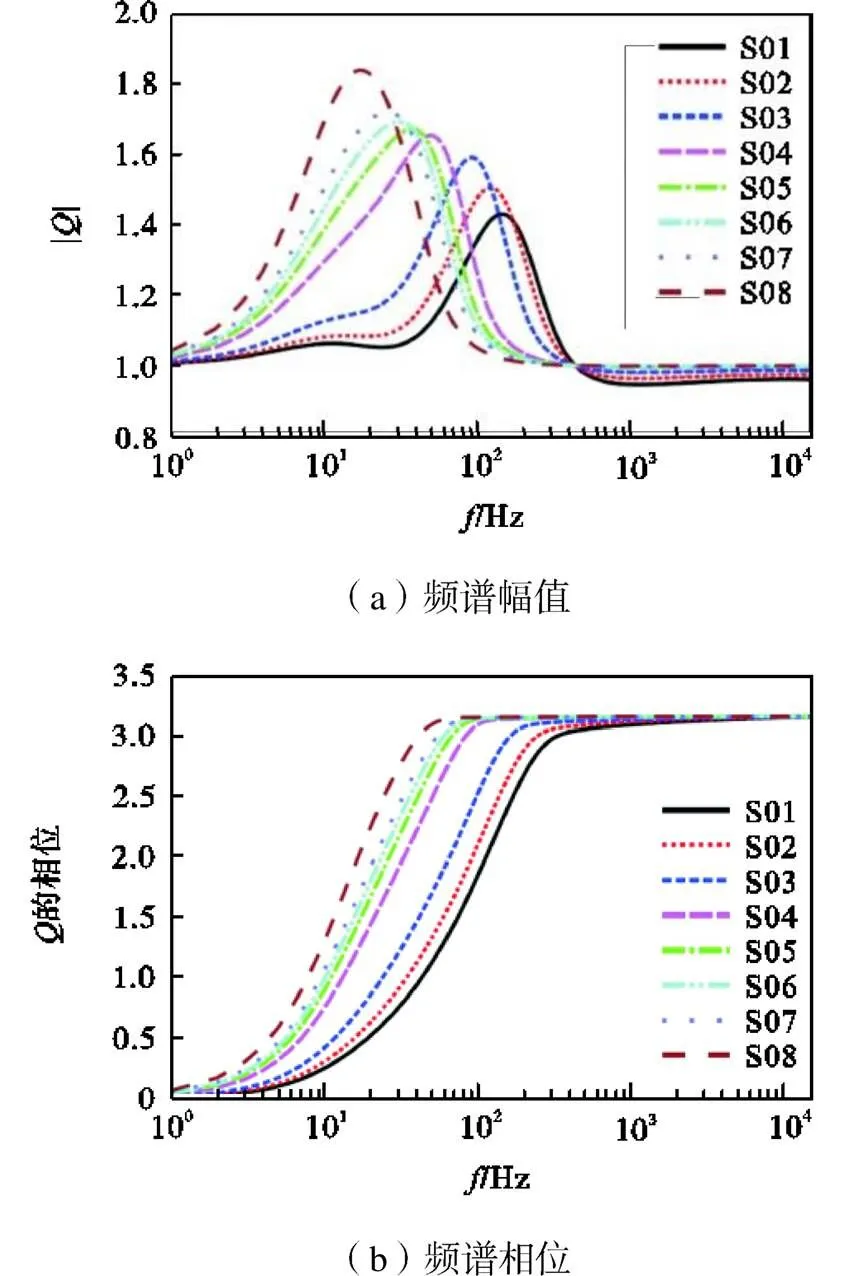
图9 虚拟源强度项

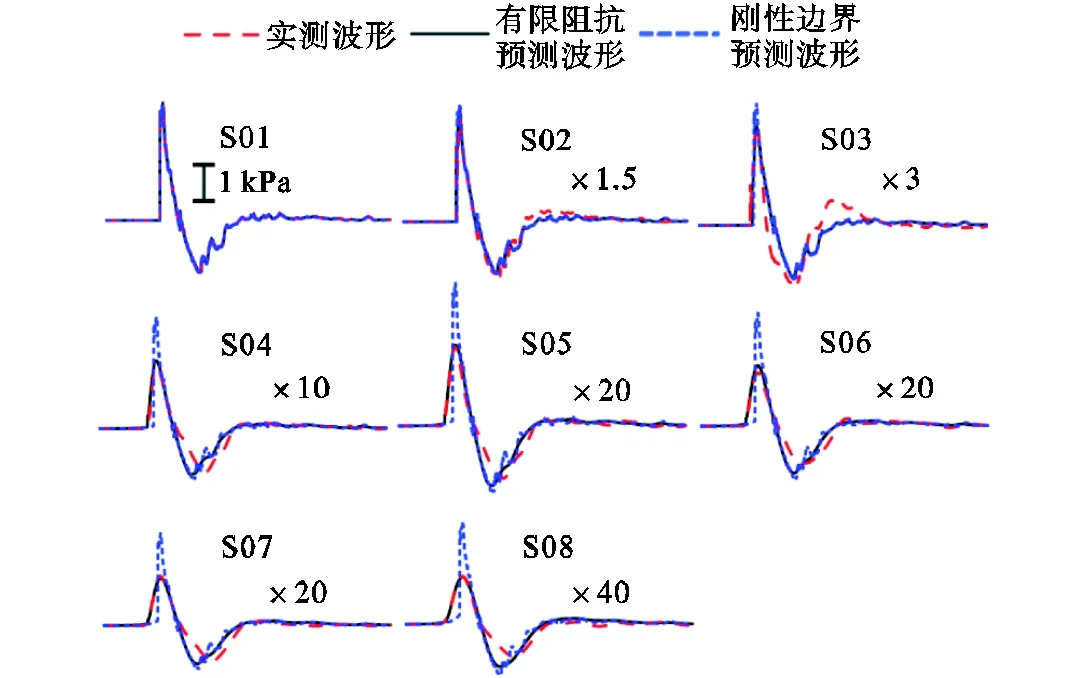
图10　　实测波形和基于S01数据和地表参数的预测波形

3 某多孔场地地面爆炸当量反演

通过以上声传播模型预测地面爆炸等效声源的源时间函数，基于预测结果建立多孔场地折合声冲量法和以多孔场地折合声冲量法为声学模型的声震分析方法，并对该场地地面爆炸当量反演精度进行讨论.

3.1 理 论

3.1.1 多孔场地折合声冲量法

各向同性介质中时域超压波形和声冲量存在以下关系[5]：

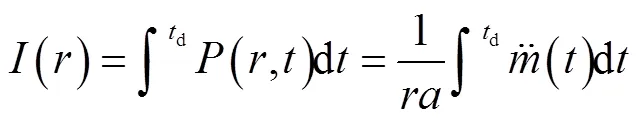
式中：为流体质量；d为脉冲正向部分持续时间；为几何扩展因子，球形扩展取4π，半球形扩展取2π．

声冲量和路径密切相关，为了表征源强度，Kim等[5]将质量流加速度的正向部分积分定义为折合声冲量，即源时间函数峰值，该参量和路径无关，

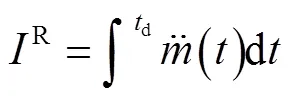
式中被积分项为源的质量流加速度．将式(11)或式(15)代入式(25)可得折合声冲量和源项关系为

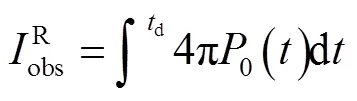
由于有限边界阻抗的声传播理论为点源假设，所以上式几何扩展因子取4π．通过以上关系，可以得到源的折合声冲量．

根据缩比关系，并将几何扩展因子取4π，折合声冲量观测值和KG85模型值存在以下关系[5,14]：

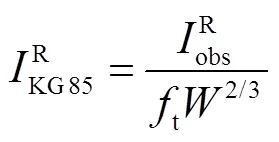
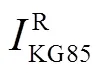
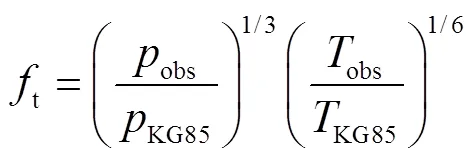
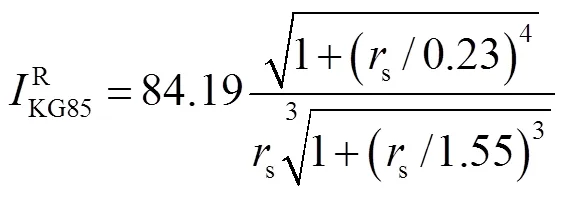
式中：KG85为KG85模型的参考环境压力，Pa；KG85为KG85模型参考环境温度，K．对于KG85模型折合声冲量，当比距离大于20m/kg1/3时，符合线性声学的变化规律[5,11]，其值接近2466.81kg/s，从而计算出当量．

3.1.2 声震分析方法

地面爆炸能量会同时耦合到空气和地介质中形成声波和地震波向远处传播，通过地震数据提供额外约束进行声震分析可提高爆炸当量预测精度[16-21].声震分析方法包括声学模型、地震波模型和数据融合方法3个部分．

对于声学模型，在式(27)基础上增加不同爆高(埋深)的声耦合系数[17]，得到基于折合声冲量的近地面声学模型，即

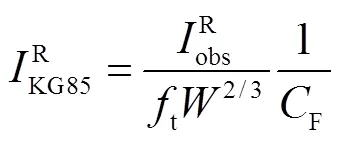
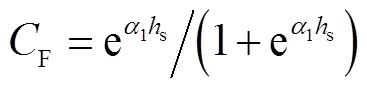
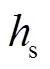
对于地震波模型，P波位移首峰值和当量、距离存在以下关系[47]：

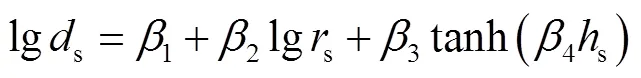
式中：s为比位移，m/kg1/3；1、2、3和4为待定系数，对于土石混合介质分别取值2.93、－1.62、－0.81和2.71．根据Sachs缩比关系[48]，比位移为

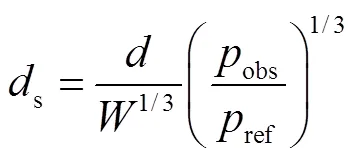
相对误差法是声震数据融合的常见方法[19]，综合误差为

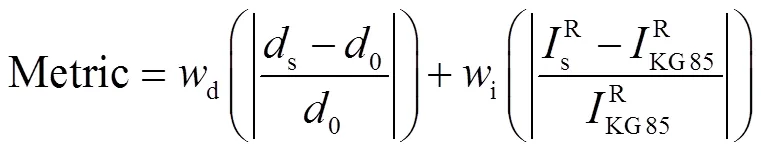
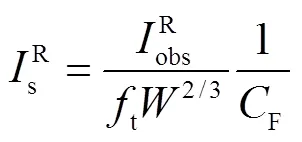
式中d和i分别为地震波和声学数据的权重，均取0.5．采用格点搜索法以最小误差为准则得到当量的最优值．

3.2 讨 论

3.2.1 多孔场地折合声冲量法反演爆源当量

由虚拟源强度项和测点超压波形得到等效声源频谱(见图11)，由图可知，等效源时间函数的主频位于20Hz以内，频率超过80Hz由于受到噪声干扰的影响，频谱幅值变化复杂．为避免噪声干扰，对源时间函数进行80Hz低通滤波，滤波后源时间函数见图12．由图可知，各个测点数据预测的源时间函数波形特征基本一致．

对源时间函数正向部分进行积分得到声冲量峰值，代入式(26)，得到折合声冲量．将折合声冲量代入式(27)～式(29)，得到爆源当量预测值(见表5原始数据预测值)．由表5可知，当量预测值相对真实值30kg明显偏小，这是由于近地面爆炸存在声震能量分配过程，部分能量耦合到地下，空气中的声能只表征爆源部分能量．

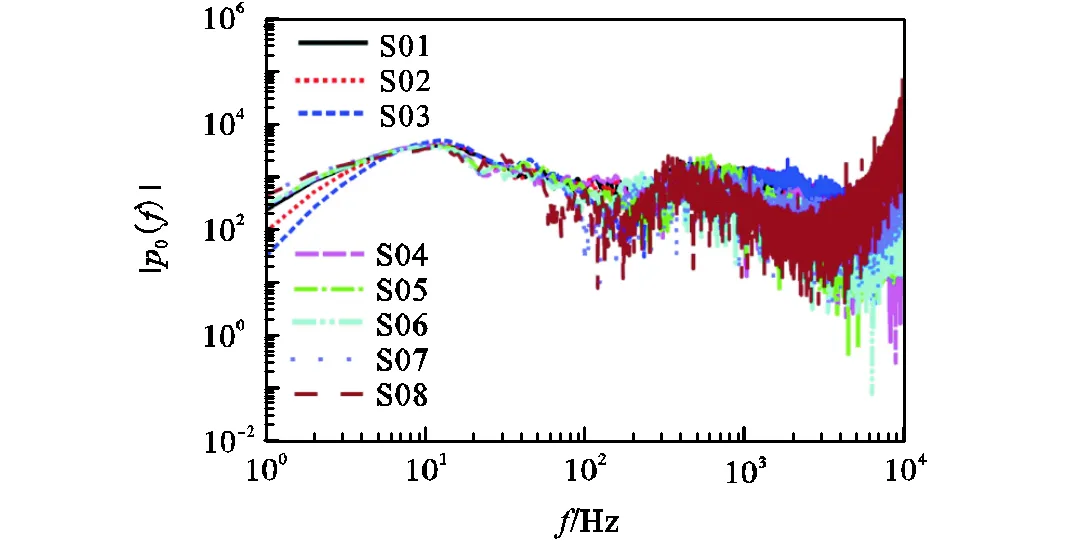
图11 等效声源频谱

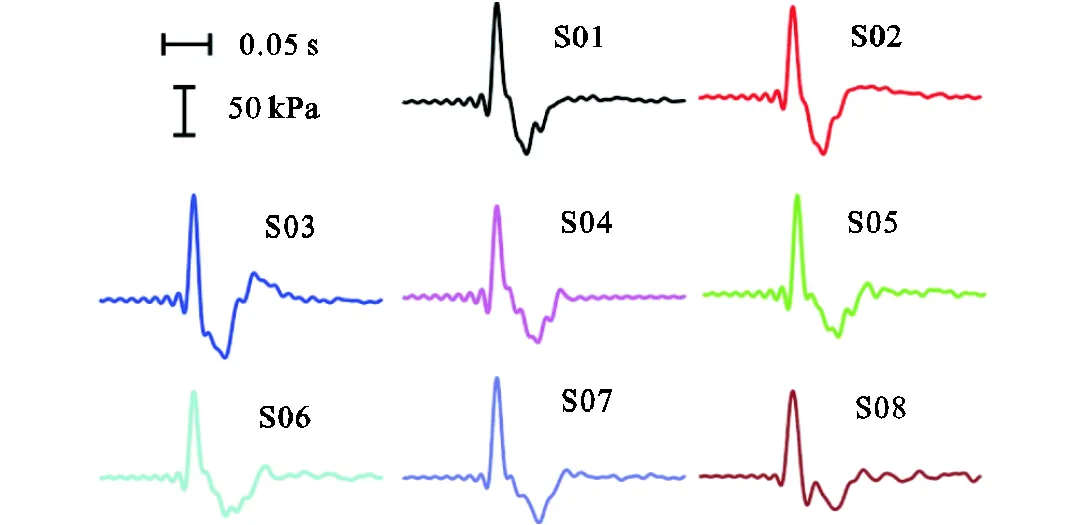
图12 等效声源的源时间函数

由于地介质为冻土，并含有大量砂砾，其介质特性和硬岩介质特性比较接近，所以声耦合系数中待定系数按硬岩介质取值．Pasyanos等[17]通过大量实测数据分析得到硬岩中待定系数为5.22，本文取该值代入式(31)得到地面爆炸声耦合系数．将折合声冲量值除以地面爆炸声耦合系数并代入式(27)～式(29)，得到爆源当量预测值(见表5考虑声震能量分配过程的预测值)．由表可知，考虑声震能量分配过程的当量预测值相对原始数据当量预测值更接近真实值，相对误差由60%减小至7%，具有较高的当量预测精度.

表5 基于有限边界阻抗的源参数估计结果

Tab.5　　Source parameter estimation results via finite boundary impedance theory

3.2.2 联合地震数据的当量反演

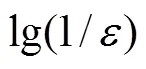
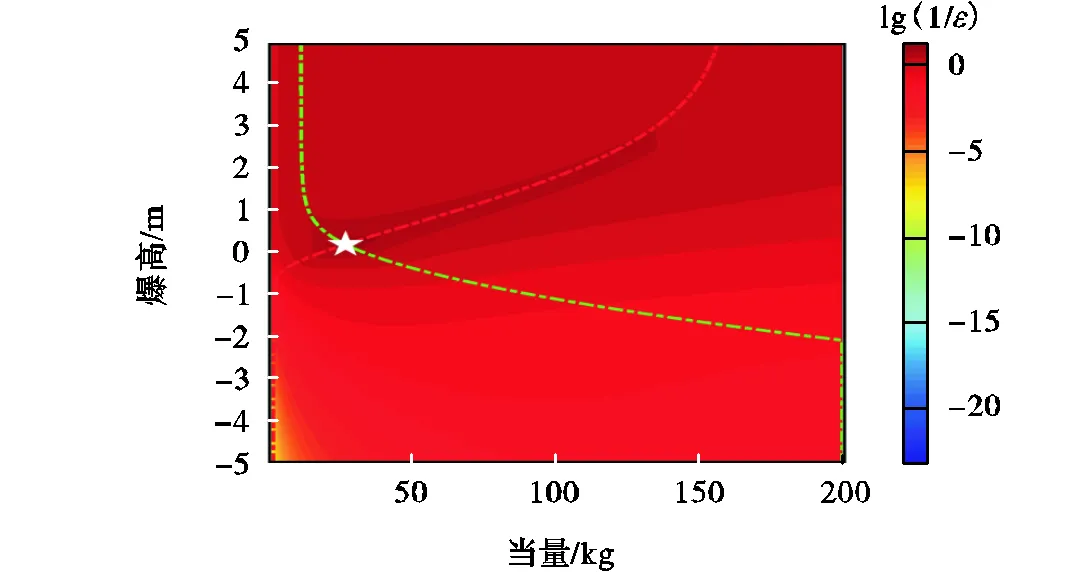
图13 基于声震分析的当量和爆高预测结果

表6 联合地震和声学数据的源参数估计结果

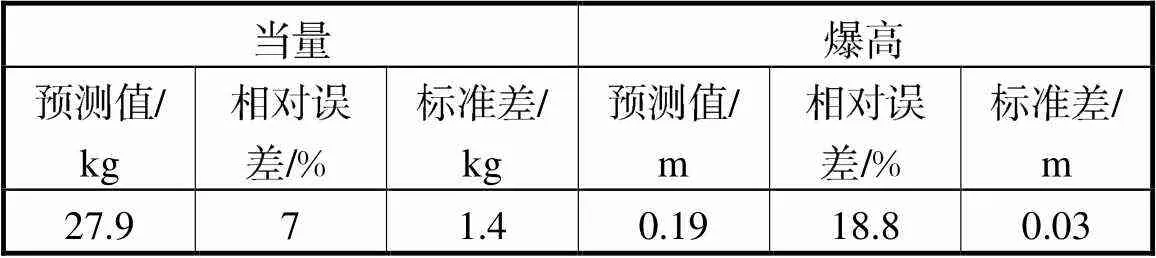
Tab.6　　Source parameter estimation results by combining seismic and acoustic data

4 结 论

本文对雪和半灌木混合覆盖地表场地的地面爆炸声传播特性和当量反演方法进行了分析，得出结论如下.

(1) 实测数据表明，雪和半灌木混合覆盖地表场地的地面爆炸声信号能量集中在低频(20Hz以内)，主频位于9～14Hz，受到多孔地表和空气吸收影响，超压幅值随距离增加快速衰减，其衰减系数1.25明显大于球面波几何扩展系数1．

(2) 基于有限边界阻抗波传播理论和四参量阻抗模型建立的声传播模型可以准确描述该多孔场地波传播特性，其预测波形和实测波形基本重合．

(3) 基于有限边界阻抗波传播理论和四参量阻抗模型建立的多孔场地折合声冲量法，通过考虑声震能量分配过程可以获得较高的当量反演精度，当量相对误差为7%．

(4) 采用以上声学反演方法并联合地震波数据进行声震分析可以准确预测多孔弹性地面附近未知爆炸事件的当量和爆高，其相对误差分别不超过7%和19%．

西北核技术研究所王占江研究员、唐仕英副研究员、刘赟哲工程师在炸药起爆方面提供了帮助和指导，谨致谢意！

［1］ 江文彬，陈 颙，彭 菲. 2019年3月江苏响水化工厂爆炸当量的估计[J]. 地球物理学报，2020，63(2)：541-550.

Jiang Wenbin，Chen Yong，Peng Fei. The yield estimation fo the explosion at the Xiangshui，Jiangsu chemical plant in March 2019[J]. Chinese Journal of Geophysics，2020，63(2)：541-550(in Chinese).

［2］ Koper K D，Wallace T C，Reinke R E，et al. Empirical scaling laws for truck bomb explosions based on seismic and acoustic data[J]. Bulletin of the Seismological Society of America，2002，92(2)：527-542.

［3］ Driels M R. Weaponeering：Conventional Weapon Sys-tem Effectiveness[M]. 2nd ed. Virginia：American Institute of Aeronautics Astronautics，Inc.，2012.

［4］ Golden P，Negraru P，Howard J. Infrasound Studies for Yield Estimation of HE Explosions[R]. USA：Air Force Research Laboratory，2011-03.

［5］ Kim K，Rodgers A. Waveform inversion of acoustic waves for explosion yield estimation[J]. Geophysical Research Letters，2016，43：6883-6890.

［6］ Arrowsmith S J，Whitaker R W，Maccarthy J K，et al. A sources-of-error model for acoustic/infrasonic yield estimation for above-ground single-point explosions[J]. InfraMatics，2012，1：1-9.

［7］ Arrowsmith S，Bowman D. Explosion yield estimation from pressure wave template matching[J]. The Journal of the Acoustical Society of America，2017，141(6)：EL519-EL525.

［8］ Kim K，Rodgers A，Wright M. Uncertainty analysis for infrasound waveform inversion：Application to explo-sion yield estimation[J]. The Journal of the Acoustical Society of America，2018，144(6)：3351-3363.

［9］ Bowman D C. Yield and emplacement depth effects on acoustic signals from buried explosions in hard rock[J]. Bulletin of the Seismological Society of America，2019，109(3)：944-958.

［10］ Schnurr J，Kim K，Garces M A，et al. Improved para-metric models for explosion pressure signals derived from large datasets[J]. Seismological Research Letters，2020，91(3)：1752-1762.

［11］ Kim K，Rodgers A R，Garces M A，et al. Empirical acoustic source model for chemical explosions in air[J]. Bulletin of the Seismological Society of America，2021，DOI: 10.1785/0120210030.

［12］ Blom P S，Dannemann F K，Marcillo O E. Bayesian characterization of explosive sources using infrasonic signals[J]. Geophysical Journal International，2018，215(1)：240-251.

［13］ American National Standards on Acoustics. ANSI S2.20—1983(ASA 20—1983)Estimating Airblast Characteristics for Single Point Explosions in Air，with a Guide to Evaluation of Atmospheric Propagation and Effects[S]. New York：American Institute of Physics for the Acoustical Society of America，1983.

［14］ Kinney G F，Graham K J. Explosive Shocks in Air[M]. New York：Springer Science＋Business Media，1985.

［15］ Douglas D A. Blast Operational Overpressure Model (BOOM)：An Airblast Prediction Method[R]. USA：Air Force Weapons Laboratory，Kirtland AFB，1987-04.

［16］ Ford S R，Rodgers A J，Xu H，et al. Partitioning of seismoacoustic energy and estimation of yield and height-of-burst/depth-of-burial for near-surface explosions[J]. Bulletin of the Seismological Society of America，2014，104(2)：608-623.

［17］ Pasyanos M E，Kim K. Seismoacoustic analysis of chemical explosions at the Nevada National Security Site[J]. Journal of Geophysical Research：Solid Earth，2018，124：908-924.

［18］ Arrowsmith S J，Johnson J B，Drob D P，et al. The seismoacoustic wavefield：A new paradigm in studying geophysical phenomena[J]. Reviews of Geophysics，2010，48(RG4003)：1-23.

［19］ Bonner J，Waxler R，Gitterman Y，et al. Seismo-acoustic energy partitioning at near-source and local dis-tances from the 2011 Sayarim explosions in the Negev Desert，Israel[J]. Bulletin of the Seismological Society of America，2013，103(2A)：741-758.

［20］ Zhang L，Li X，Liang X，et al. Improved seis-moacoustic analysis model and its application to source parameter inversion of near-surface small-yield chemical explosions[J]. Applied Geophysics，2021，18(1)：17-30.

［21］ Ford S R，Bulaevskaya V，Ramirez A，et al. Joint bayesian inference for near-surface explosion yield and height-of-burst[J]. Journal of Geophysical Research：Solid Earth，2021，126(2)：e2020JB020968.

［22］ Ford R D，Saunders D J，Kerry G. The acoustic pres-sure waveform from small unconfined charges of plastic explosive[J]. The Journal of the Acoustical Society of America，1993，94(1)：408-417.

［23］ Attenborough K，Renterghem T V. Predicting Outdoor Sound[M]. 2nd ed. Boca Raton and Oxon：CRC Press，2021.

［24］ Kaynia A M，Løvholt F，Madshus C. Effects of a multi-layered poro-elastic ground on attenuation of acoustic waves and ground vibration[J]. Journal of Sound and Vibration，2011，330：1403-1418.

［25］ Albert D G，Decato S N，Carbee D L. Snow cover effects on acoustic sensors[J]. Cold Regions Science and Technology，2008，52：132-145.

［26］ Crocker M J. Handbook of Noise and Vibration Control[M]. Hoboken，New Jersey：John Wiley & Sons，Inc.，2007.

［27］ Albert D G. Observations of acoustic surface waves in outdoor sound propagation[J]. The Journal of the Acous-tical Society of America，2003，113(5)：2495-2500.

［28］ Attenborough K，Taherzadeh S. Propagation from a point source over a rough finite impedance[J]. The Jour-nal of the Acoustical Society of America，1995，98(3)：1717-1722.

［29］ Albert D G，Hole L R. Blast noise propagation above a snow cover[J]. The Journal of the Acoustical Society of America，2001，106(6)：2675-2681.

［30］ Albert D G，Orcutt J A. Acoustic pulse propagation above grassland and snow：Comparison of theoretical and experimental waveforms[J]. The Journal of the Acoustical Society of America，1990，87(1)：93-100.

［31］ Albert D G. Acoustic waveform inversion with applica-tion to seasonal snow covers[J]. The Journal of the Acoustical Society of America，2001，109(1)：91-101.

［32］ Attenborough K. Ground parameter information for propagation modeling[J]. The Journal of the Acoustical Society of America，1992，92(1)：418-427.

［33］ Attenborough K. Review of ground effects on outdoor sound propagation from continuous broadband sources [J]. Applied Acoustics，1988，24：289-319.

［34］ Pao S P，Evans L B. Sound attenuation over simulated ground cover[J]. The Journal of the Acoustical Society of America，1971，49：1069-1075.

［35］ Donato R J. Propagation of a spherical wave near a plane boundary with a complex impedance[J]. The Journal of the Acoustical Society of America，1976，60(1)：34-39.

［36］ Attenborough K. Propagation of sound above a porous half-space[J]. The Journal of the Acoustical Society of America，1980，68(5)：1493-1501.

［37］ Nicolas J，Berry J L，Daigle G A. Propagation of sound above a finite layer of snow[J]. The Journal of the Acoustical Society of America，1984，77(1)：67-73.

［38］ Delany M E，Bazley E N. Acoustical properties of fi-brous absorbent materials[J]. Applied Acoustics，1970，3(2)：105-116.

［39］ Attenborough K. Acoustical impedance models for out-door ground surfaces[J]. Journal of Sound and Vibration，1985，99(4)：521-544.

［40］ Johnson D L，Koplik J，Dashen R. Theory of dynamic permeability and tortuosity in fluid-saturated porous me-dia[J]. Journal of Fluid Mechanics. 1987，176：379-402.

［41］ Champoux Y，Stinson M R，Daigle G A. Air-based system for the measurement of porosity[J]. The Journal of the Acoustical Society of America，1991，89(2)：910-916.

［42］ Lafarge D，Lemarinier P，Allard J F，et al. Dynamic compressibility of air in porous structures at audible frequencies[J]. The Journal of the Acoustical Society of America，1997，102(4)：1995-2006.

［43］ Rudnick I. The propagation of an acoustic wave along a boundary[J]. The Journal of the Acoustical Society of America，1947，19(2)：348-356.

［44］ Brekhovskikh L M. Waves in Layered Media[M]. New York：Academic Press，1980.

［45］ Kim K，Rodgers A. Influence of low-altitude meteoro-logical conditions on local infrasound propagation invest-tigated by 3-D full-waveform modeling[J]. Geophysical Journal International，2017，210：1252-1263.

［46］ 全国声学标准化技术委员会. GB/T 17247.1—2000 声学户外声传播衰减第1部分：大气声吸收的计算[S]. 北京：中国国家标准化管理委员会，2000.

National Technical Committee on Acoustics of Standardization Administration of China. GB/T17247.1—2000 Acoustics—Attenuation of Sound During Propagation Outdoors—Part 1：Calculation of the Absorption of Sound by the Atmosphere[S]. Beijing：Standardization Administration of China，2000(in Chinese).

［47］ Zhang Liangyong，Tang Shiying，Lu Qiang，et al. Yield estimation model and its accuracy analysis for near-surface explosions of soil-rock-mixture site[C]//Ahmad H B. 2021 5th International Conference on Mechanics，Mathmatics and Applied Physics(ICMMAP 2021). UK：IOP Publishing，2021：012076.

［48］ Sachs R G. The Dependence of Blast on Ambient Pressure and Temperature[R]. USA：Army Ballistic Research Laboratories，1944.

Sound Propagation Characteristics and Yield Inversion Analysis of Surface Explosion at the Specific Poroelastic Site

Zhang Liangyong1, 2，Lu Qiang2，Liang Xubin2，Li Pengyi2，Fang Houlin2，Zeng Xinwu1

(1. College of Meteorology and Oceanology，National University of Defense Technology，Changsha 410073，China；2. Northwest Institute of Nuclear Technology，Xi’an 710024，China)

Surface explosion power prediction is critical in production and living safety and weapon performance tests. To solve the yield prediction problem of surface explosions at the specific poroelastic site where the ground is covered by snow and sparsely distributed subshrubs, the sound propagation characteristics of surface explosions at the poroelastic site were examined using experimental data. Then, using the finite boundary impedance theory and a four-parameter model, the acoustic propagation model was established to understand the sound attenuation characteristics. Based on the aforementioned acoustic propagation model, the surface explosion yield of a poroelastic site was predicted using the reduced acoustic impulse (RAI) method, and a seismoacoustic analysis method using the RAI acoustic model of a poroelastic site was established to inverse and analyze the surface explosion yield of the poroelastic site. The results show that the signal energy of the surface explosion at the specific poroelastic site is concentrated at low frequencies with the maximum frequency < 20Hz, overpressure amplitude decaying rapidly with distance, and the attenuation coefficient exceeding 1.25, which is higher than the spherical-wave geometrical attenuation coefficient of 1 owing to the influence of the poroelastic surface and air absorption. The poroelastic-site wave propagation model established by the wave propagation theory of finite boundary impedance and four-parameter model exhibits excellent performance in predicting waveforms that substantially coincide with the measured waveforms. Based on the aforementioned model, the RAI method is applied to the prediction of surface explosion yield, which is proved to have high prediction accuracy of yield whose relative error is no more than 7% with consideration of seismoacoustic coupling. Seismoacoustic analysis by integrating seismic data and the aforementioned acoustic method is discussed and found that the yield and height-of-burst of an unknown explosion event near the poroelastic ground can be predicted accurately with the relative errors of no more than 7% and 19%, respectively.

surface explosion；finite boundary impedance；four-parameter model；reduced acoustic impulse (RAI)；seismoacoustic analysis

O389

A

0493-2137(2023)01-0037-10

10.11784/tdxbz202112037

2021-12-24；

2022-03-28.

张亮永（1990—  ），男，硕士，助理研究员，zhangliangyong18@nudt.edu.cn.

曾新吾，xinwuzeng@nudt.edu.cn.

国家自然科学基金资助项目(12072290).

Supported by the National Natural Science Foundation of China(No. 12072290).

(责任编辑：田 军)