地震作用下山区陡坡地段桥梁地震响应分析

张 洁，曾金明，游 姗，付小红

（1.武昌工学院，武汉 430065；2.中交第二公路勘察设计研究院有限公司，武汉 430056）

随着我国交通的蓬勃发展，出现了越来越多的陡坡桥梁，修建在陡坡上的桥梁有潜在的失稳问题，并且受力复杂。在地震作用下，边坡的滑坡失稳会引起桩基冲击破坏，进而引起桥梁上部结构的破坏，造成严重的经济损失和人员伤亡，因此对陡坡桥梁进行地震响应分析十分必要。

近年来，有不少学者对陡坡桥梁进行了研究，车竞[1]对山区陡坡地段桥梁桩基地形地质、受力模式及施工条件等进行分析，并结合广东省某山区高速公路工程实例对陡坡地段桥梁桩基受力特点展开研究，探讨山区陡坡地段桥梁桩基的设计理念和设计方法。常前永[2]以粘弹性人工边界为基础，建立不同参数下的陡坡模型和桩基模型，分析了不同参数对陡坡动力响应和桥梁桩基动力响应的影响。刘晶波等[3]以ANSYS有限元软件为例，给出了粘弹性人工边界及其地震动输入在大型通用有限元软件中的实现捷径，对其他有限元软件在程序中的实现也有一定的参考价值。

苏连虎[4]以工程实例为背景，对陡坡桩基进行方案对比，从安全、经济、适用、环保4个方面进行对比分析，对陡坡桥梁的建设提供了参考价值。张伟[5]对复杂山区地带高山陡坡稳定进行分析，并以工程实例为研究对象，分析在实际施工过程中需要注意的事项及应用效果，为实际工程设计提供参考。杨明辉[6]采用数值流形方法解决了桩岩接触面不连续变形的问题和桩周岩体的本构模型的确定问题，并且通过参数分析了桩侧下滑推力、桩基内力、桩基位移、岩质边坡基桩受力的规律。王小红等[7]采用三维非线性有限元法，对陡坡桥梁的单桩与排桩进行对比分析，在设计过程中选取合适的桩径、桩长和嵌岩深度。本文以山区陡坡桥梁为研究对象，采用Midas有限元软件建立有限元模型，考虑陡坡对桩基地震响应的影响。

1 陡坡桥梁有限元模型建立

1.1 工程概况

月湖坪大桥右线桥采用4×40 m+4×40 m+3×40 m三联预应力连续T梁。桥墩采用多圆柱墩配圆桩基础、薄壁墩配群桩基础、空心墩配圆桩基础。其中墩高分别为12、36、50、60、72、78、76、54、28、6 m。其中1、2、9、10号墩为柱径2.0 m配桩径2.2 m的柱式墩，3、8号为6.5 m×2.6 m的薄壁墩，4、5、6、7为6.5 m×3.5 m的空心墩。

桥梁采用的普通钢筋有HPB300、HRB400和HRB500，其中直径大于22 mm的钢筋采用HRB500的钢筋。主梁采用C50混凝土、柱式墩采用C30混凝土，薄壁墩与空心墩均采用C40混凝土，桩基均采用C30混凝土。

1.2 有限元模型建立

采用Midas建立桥梁的全桥计算模型，其中主梁、桥墩、桩基和系梁等均采用梁单元进行模拟，支座采用弹性连接单元进行模拟。按照m法（计算弹性桩水平位移及作用效应的方法）计算土弹簧的刚度，选择M动=2×M静进行计算。桥梁的计算模型如图1所示。

图1 桥梁计算模型

1.3 动力特性

根据建立好的桥梁计算模型进行桥梁动力特性分析。表1为桥梁的前十阶周期及频率，图2为不考虑陡坡时桥梁的前6阶振型图。

从表1和图2可以看出：

图2 无考虑陡坡时桥梁前6阶振型

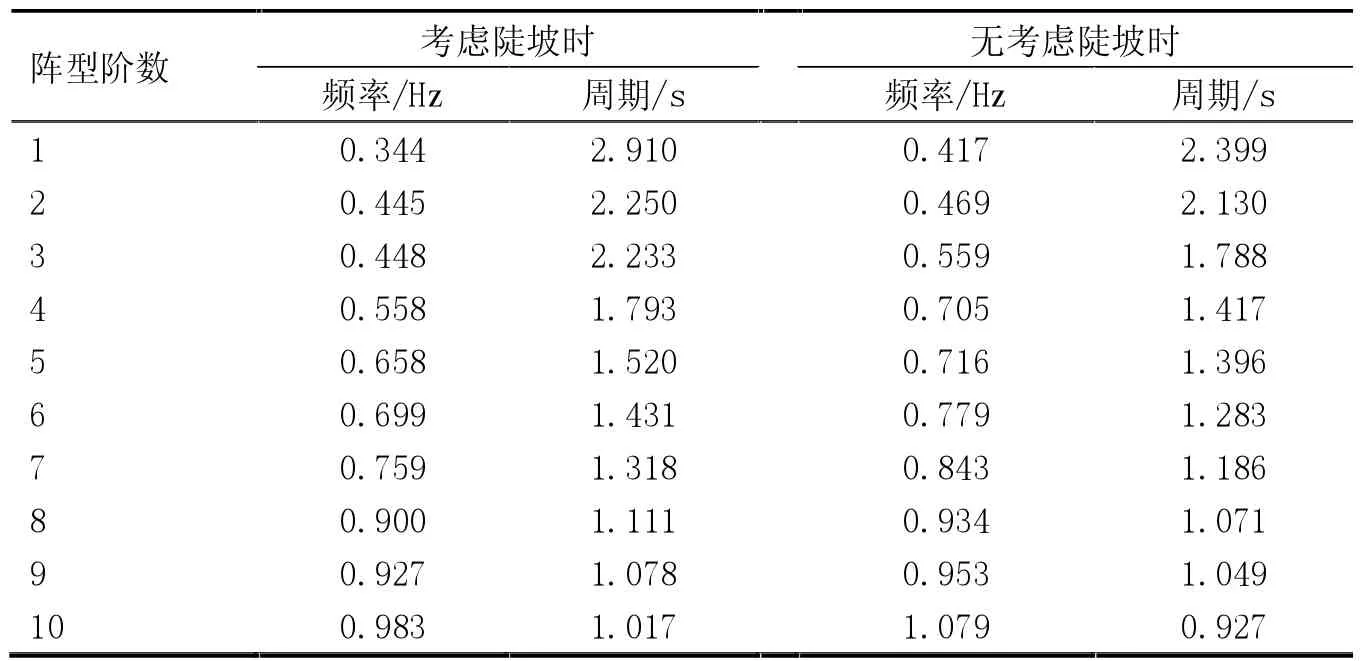
表1 桥梁前十阶周期及频率

1）两种模型的第1振型均为横向弯曲，考虑陡坡时基频是0.344，仅是第2阶振型频率的77%，不考虑陡坡时的基频为0.417，是第2阶振型频率的89%。

2）两种模型的第2阶振型均为纵向弯曲，第3、4阶均为横向弯曲；考虑陡坡时第5阶振型为横向弯曲，第6阶振型为纵向弯曲，而不考虑陡坡时的第5阶振型为纵向弯曲，第6阶振型为横向弯曲。

3）考虑陡坡会延长桥梁的周期，相比于不考虑陡坡时，考虑陡坡时的第1阶周期增长率为17.56%，第2～6阶的增长率分别为5.33%、19.93%、20.97%、8.16%、10.34%。

2 地震响应分析

2.1 线性地震响应分析

按照公路桥梁抗震细则现只考虑水平地震作用、对桥梁进行地震响应分析。

现地震作用效应与永久作用效应组合（组合一：永久效应+地震作用效应；组合二：永久效应-地震作用效应）及桥梁地震响应见表2。

表2 地震作用下桥墩主要截面内力

为了对比分析考虑陡坡和不考虑陡坡对桥梁地震响应的影响，对不考虑陡坡模型进行地震响应分析，两种模型计算的顺桥向各号墩墩底弯矩组合一的影响值如图3所示。

由图3可以看出，采用陡坡模型时桥墩的地震弯矩响应比不考虑陡坡时的弯矩响应值小，考虑陡坡时1号墩顺桥向墩底的弯矩值是2 956 kN·m，不考虑陡坡时1号墩顺桥向墩底的弯矩值是2 804 kN·m，相比于不考虑陡坡时，采用陡坡模型1号墩墩底弯矩减小5.14%。

图3 顺桥向各号墩墩底弯矩响应值

2.2 非线性地震响应分析

在进行非线性地震作用时，延性构件采用有效抗弯刚度计算，其他构件抗弯刚度仍按毛截面计算。现根据本桥桥墩的配筋情况，钢筋采用理想弹塑性模型，混凝土采用mander约束混凝土模型计算桥墩弯矩-曲率曲线。由于篇幅有限，仅列出1号墩和5号墩的弯矩曲率，表3为1号墩和5号墩的弯矩曲率关系表。

表3 弯矩曲率关系表

桥墩采用有效抗弯刚度计算，对桥梁进行非线性地震响应分析。对活动盆式支座的活动方向，忽略其摩擦力的作用。对于连续墩，由于设置了4根较大的抗震锚栓，为了考虑其作用，现将其刚度与支座的刚度进行并联叠加处理。

对两种计算模型进行非线性地震作用，对比分析两种计算模型对桥梁地震响应的影响，两种模型计算的顺桥向各号墩墩底弯矩组合一的影响值如图4所示。

由图4可以看出，采用陡坡模型时桥墩的地震弯矩响应比不考虑陡坡时的弯矩响应值要小，考虑陡坡时1号墩顺桥向墩底的弯矩值是2 763 kN·m，不考虑陡坡时1号墩顺桥向墩底的弯矩值是2 901 kN·m，相比于不考虑陡坡时，采用陡坡模型1号墩墩底弯矩减小4.76%。

图4 非线性地震作用下墩底弯矩响应值

3 结论

（1）相比于不考虑陡坡，考虑陡坡时桥梁的周期会增长，这是因为考虑陡坡时，桥梁整体的刚度会变小，除此之外，考虑陡坡会改变桥梁结构的振型。

（2）相比于不考虑陡坡，考虑陡坡时能够减缓地震对桥墩的作用，从而使桥梁结构的内力减小，减小率基本上为5%，这是因为考虑陡坡计算的桥梁整体刚度小，地震效应也小。

（3）考虑桩基础周围土对结构影响时，是根据现场的地势和地质条件进行准确模拟的，更能符合实际的工程情况，山区陡坡桥梁考虑陡坡模拟的方法更与实际工程吻合。