基于非等权聚类混合PSO-SVR的短期空气质量预测模型研究

邓国取, 陈 虎

(河南科技大学 管理学院,河南 洛阳 471023)

0 引言

空气质量与人类日常健康生活息息相关。作为生命的四大要素之一,空气在维持生态系统方面起着重要作用。近年来,人类活动严重加剧了空气污染程度,空气质量已成为全社会广泛关注的焦点问题。因此研究影响空气质量的因素,合理预测空气质量(Air Quality Forecasting,AQF)对大气污染监管和治理有着重要的现实意义[1]。目前的研究将AQF分为短期AQF(Short Air Quality Forecasting,SAQF)、中期AQF和长期AQF。中长期AQF通常用作较长时间内的空气质量预测,主要用于规划工业用地或居住区的分布以及实现中长期精细化预报,为污染防控和达标规划提供更多的提前量。SAQF常用于辅助调控短期内的交通网络,还可辅助个人出行,预防本人过度暴露于外部污染环境中。因此,SAQF对社会发展和人们的日常生活都具有重要意义。

SAQF常用的是混合预测模型,为克服支持向量回归(Support Vector Regression,SVR)在处理海量数据方面的不足, GHAEMI等[2]首次建立了基于Hadoop平台的分布式计算模型。SHAH等[3]引入人工蜂群误差最小化的参数优化算法思想和SVR结合用于空气质量预测,所提出的混合模型具有更高的预测性能。但广泛使用的算法包括蚁群优化(Ant Colony Optimization,ACO),遗传算法(Genetic Algorithm,GA)等算法不能很好地存储粒子信息。同时,上述算法参数优化时间较长,不能最大程度发挥SVR算法的优势[4,5]。随着计算机性能的不断提高,研究人员在早期神经网络的基础上引入长短期记忆网络(Long Short-Term Memory Recurrent Neural Network,LSTM)对空气质量进行预测,但忽略了多因素对单一空气污染物的影响[6-8]。

目前,国内外学者对空气质量的研究主要集中对空气质量指数(Air Quality Index,AQI)的研究。国内学者大多是基于2012年3月国家发布的空气质量评价标准《环境空气质量标准》(GB 3095-2012),将PM2.5,PM10,SO2,CO,NO2和O3这6种污染物用统一的AQI作为评价标准。罗宏远等[9]提出AQI不仅可以直观地呈现出空气质量的变化趋势,还可直接服务于政府工作者和相关群体。部分研究表明,除6大污染物以外,气象因素如气温、天气、风速、风向等也是影响AQI预测的重要因素[10,11]。许文轩等[12]在华北地区AQI的时空分布规律研究中引入空间异质性和空间相关性的思想,分析了经济和自然因素对空气质量产生的影响。但现有大多数研究在测量AQI时多采用污染物浓度或气象等直接因素,忽略了社会发展过程中工业化和城市化等直接或间接因素对AQI的影响。龚光彩等[13]以北京市为例,建立了没有考虑社会经济因素的区域环境关联模型。事实上,AQI是直接因素和间接因素的综合表现结果,用单一的直接因素测量AQI不够充分,可能存在测量误差,从而会降低模型的预测精度。李静萍和周景博[14]首次采用结构方程模型(Structural Equation Model,SEM)分析工业化和城市化对城市空气质量的影响,不仅可以用观测变量代替不可测的潜变量,还可以容许测量指标存在的误差,从而能更精确地估计各因素对空气质量的影响。

综上所述,本研究基于历史气象数据,首先使用相关方法筛选影响空气质量预测的重要气象因素,并构建结构方程模型探究经济社会发展中工业化和城市化两大指标对空气质量的影响,筛选出对空气质量影响较大的非气象影响因素;其次为提高实验数据的规律性,依托SVR处理小样本的优势,运用K-means聚类算法把数据拆分成若干类别的小规模数据;最后将粒子群优化算法(Particle Swarm Optimization,PSO)与SVR结合,建立混合PSO-SVR模型提高空气质量的预测精度,以期为社会生产发展和人民生活提供服务。

1 混合PSO-SVR模型原理

1.1 SVR原理

支持向量机是一种常用的判别方法,它遵循SRM原理,在处理小样本和高维特征空间问题上具有独特的优势。支持向量机最初用于解决模式识别问题,但近年来通过引入不敏感损失函数ε来处理非线性回归估计问题。支持向量机用于解决回归问题时被称为支持向量回归(Support Vector Regression,SVR),其主要思想是通过使用非线性函数将数据集xi(i=1,…,n)映射到一个高维特征空间。具体关系表示为:

f(x)=ωTφ(x)+b

(1)

其中,f(x)为输出值,ω和b为系数,φ(x)为非线性映射函数,可以将输入值转换为高维特征空间。ω和b的调控值如下:

(2)

其中,Rε()是经验风险,C是正则化参数,也即惩罚因子。

(3)

(4)

K(xi,xj)=φ(xi)φ(xj)

(5)

目前研究中常用的有3类核函数,包括多项式核函数、Sigmoid核函数和高斯核函数。多项式核函数是维数最高的且该类函数的计算灵也较大,从而导致该类函数的误差值较高。对于Sigmoid函数而言,只有部分数值符合Mercer定理条件,其适用局限性导致部分数值无法保证函数的正定性。而高斯核函数在SVR研究中是最常用的一种,也被称为径向基核函数(Radial Basis Function,RBF)。该函数可以将数据映射到无限维,且计算复杂度相对更低。因此本研究采用RBF作为支持向量回归的核函数,函数的定义为:

(6)

1.2 PSO原理

在SVR模型中,预测精度主要受不敏感损失变量ε、径向基核系数变量γ以及惩罚因子c等变量的影响。构建PSO-SVR混合模型的目的就是进行参数寻优,找到SVR中最佳参数组合以此来提高预测精度。在进行SVR回归预测前,需要确定惩罚因子c、径向基核系数变量γ和不敏感损失变量ε。惩罚因子c过小会导致预测精度大幅降低,从而导致泛化能力变差,但c过大将会导致容忍度较低,从而预测精度降低。在进行参数寻优过程中,本研究将以惩罚因子c较小的原则进行选择。径向基核系数变量γ控制SVR对输入变量的敏感程度。不敏感损失变量ε表示容忍模型误差的能力,代表拟合边界的宽度,在实验过程中应尽可能多的使样本位于拟合边界上。因此,为达到参数组合的最优,采用粒子群优化算法对参数进行选择。

粒子群优化是在迭代优化的基础上发展起来的种群计算技术。首先,初始化一组粒子,然后通过跟踪单个极值pibest和全局极值pgbest来更新这些粒子在下一次迭代中的速度和位置;当发现这两个端点后,PSO算法将对每个粒子的速度和距离进行识别。

假设在i维搜索空间中存在m个粒子。第i个粒子表示为xi=(xi1,…,xid),其中i=1,…,m。也就是说,第i个粒子的位置为xi。第i个粒子的速度也是一个矢量,用vi=(vi1,…,vid)表示。该粒子的最优位置为pi=(pi1,…,pid),而整个种群的最优位置为pg=(pg1,…,pgd)。标准的粒子群算法更新了现有的粒子群算法,具体的定义如下:

(7)

(8)

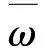
(9)

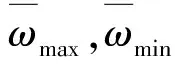
1.3 混合模型构建

混合PSO-SVR算法的整体流程如图1所示。

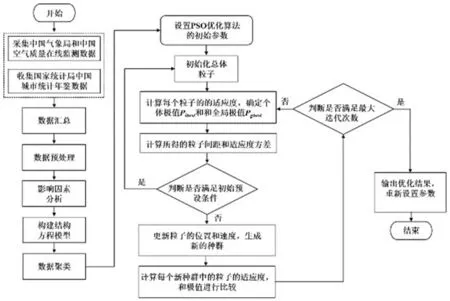
图1 聚类混合PSO-SVR建模流程图

首先采用逐步回归的方法将污染物数据、气象数据和时间特征数据进行降维处理;其次为更好体现SVR对小样本数据处理的优势,采用K-means对降维处理后的数据进行聚类划分;最后将聚类划分后的小样本数据输入到PSO-SVR模型中进行数值预测。具体步骤如下:

步骤1在进行逐步回归降维处理前,假设实验数据中存在c条样本数据,n个自变量(特征处理后的变量数据),则该集合可表示为X=(X1,…,Xn),本研究中的因变量AQI用Y表示,如下所示:

Y=β0+βiXi+ε,i=1,…,n

(10)

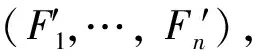
步骤2建立因变量Y与自变量子集{Xτ1,X1},…,{Xτ1,Xn}的二元回归模型,共有n-1个,再次计算回归系数以及对应的F检验统计量的值为Fk″(k∉S1) ,令Fτ2″为其中的最大值;在给定显著性水平α=0.05下,对应的临界值为F(2),当Fτ2″≥F(2),则将Xτ2加入到回归模型中,否则结束变量引入过程。

步骤3重复步骤2的操作,得到本研究最终的所需要的方程模型如下:

(11)

步骤4选择l个质心,将经过特征编码后的原始数据乘上对应的系数βi后,将新的数据集Yτ输入到K-means聚类算法中得到l个数据集合,分别为u1,…,ul∈Rn,Yτi∈Rn,i=1,…,c,计算数据集Yτ中每一个样本到质心uj的欧氏距离,不断更新集合的质心,将其归为l个集合,具体计算公式如下:

(12)

步骤5将每个集合Si中的30%作为测试集,最后输入到PSO-SVR模型中得到S(Si,P(c,γ,ε))即为AQI的预测结果。

2 数据实验与分析

2.1 数据来源

本研究借助Python相关工具PyCharm收集中国气象总局发布的2017年1月1日至2019年12月31日全国34个省份的历史空气质量指数(AQI)以及气象因素(温度、风向、风力、降雨、压强以及湿度等,通过计算近三年各地区年均AQI显示,北京市,天津市,山东省,河北省,山西省,陕西省,河南省,安徽省,新疆等9个地区的空气污染在近三年中表现较为严重,为验证混合模型的优越性,将以北京市,天津市以及其他7个地区省会城市的气象数据为基础,同时使用数据采集器收集中国空气质量在线监测分析平台发布的2017年1月至2019年12月这9个城市的每日六大污染物浓度。然后将AQI,气象因素、污染物及工业化和城市化因素作样本数据展开研究。

2.2 评价指标

研究选择均方误差(Root Mean Square Error,RMSE)和平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)来检验所提出的混合模型的预测性能。其计算公式为:

(13)

(14)

(15)

(16)

2.3 结果比较

本研究选择GA-SVR,BPNN,XGBoost和LSTM四个模型分别对加入工业化和城市化因素的实验数据进行测试。选择GA-SVR模型的原因是,为了对比突出PSO优化参数效果比GA算法更适用于该模型。选择人工神经网络ANN中的BPNN模型,主要原因是该模型在实验数据较少时,通过径向基神经元和线性神经元建立广义回归神经网络较稳定,从而保证较好的预测效果。选择XGBoost模型的原因是可以提供并行树提升,进而能快速准确地解决大样本数据,但由于短期空气质量预测的样本数据规模有限,采用该模型可能会由于样本数量导致模型训练效果不够优良,从而降低预测精度。选择LSTM的原因是随着计算机性能的不断提高,在早期神经网络的基础上开发的卷积神经网络、循环神经网络和LSTM等得到应用,其中,LSTM在六大污染物浓度预测上的效果优于其它模型。本研究选择Tensorflow框架下Keras中的LSTM方法和混合模型PSO-SVR进行比较,探究二者在高峰值的拟合效果,以此进一步验证混合模型的优良性。如表1所示,展示了9个城市在5种模型下测验后的平均结果。

表1 模型的评价指标

BPNN,XGBoost和LSTM模型在本研究中采用实验前设置的默认参数。通过实验可知,混合PSO-SVR的评价指标优于其他模型、模型的预测时间也是最短,进一步验证了本研究提出的混合PSO-SVR模型的优良性。

3 总结与展望

本研究将粒子群算法和支持向量回归、结构方程模型和K-means聚类相结合,构建了非等权聚类混合PSO-SVR模型,并以中国地区的9大城市为例进行了性能测试。首先对数据进行初步预处理,分析时间影响因素以及气象影响因素,然后结合经济社会发展中工业化和城市化影响因素构建结构方程模型,最终将最优变量组合输入基于K-means聚类的混合PSO-SVR模型,同时进行比较分析验证所提出的混合模型的性能。结果显示混合模型在预测精度和运行时间方面都占据一定的优势。本研究的主要贡献可归纳如下:(1)不仅计算了影响AQI的最优的气象变量组合,而且还引入结构方程模型探究了经济社会中工业化和城市化因素对空气质量的非直接影响,以此提高了AQI预测精度;(2)引入无监督聚类算法K-means,增强了建模数据的规律性,减少了单次数据预测量,提高了预测精度的同时缩短了运行时间。此外,借助 PSO优化算法实现参数的自动选择,克服了SVR收敛过早问题;(3)通过选取中国地区具有代表性的2个直辖市和7个省会城市进行模型的检验,验证了该模型的可实用性;同时选择GA-SVR,BPNN,XGBoost和LSTM四个模型做对比,进一步验证了加入工业化和城市化因素后,本研究提出的混合PSO-SVR模型优于其他四个模型,在高峰值的拟合中表现较为稳定。空气质量的变化对自然生态系统和经济社会的影响正在加速,重视并提高我国对空气质量状况的预测,加强气候变化研究至关重要。因此为增强本研究所提出的模型的适应度和准确度,下一步工作将重点研究工业化和城市化进程对大气污染物浓度的影响,尽可能为绿色经济社会发展提出针对性的政策和建议。