考虑文本情感特征的电商小微企业信用风险预警

2023-02-22鲍新中

运筹与管理 2023年12期

徐鲲, 李莹, 鲍新中

(北京联合大学管理学院,北京 100101)

0 引言

目前以电商小微企业为研究对象的信用风险预警指标体系初具雏形,但并未形成定论。学者们进一步强调了定性指标对小企业信用风险评估的重要性[1,2],这意味着构建电商小微企业信用风险的指标体系必须契合电商小微企业特性。随着云计算、大数据在信息采集、智能决策等方面为互联网融资赋能,信用风险评估视角得以扩展:通过挖掘云计算库中储存的多层次、多维度、时效性强的结构化数据与非结构化数据[3],以多维度动态数据分析小微企业的经营流水、营收趋势、交易网络[4]、客户交易行为[5]等。在形式多元化的数据中,学者们逐渐聚焦蕴含丰富信息的文本,李成刚等[6]指出上市公司信息披露文本的可读性、相似度、情感语调能深度反应公司信用风险。而对于电商小微企业而言,最具特点的非结构化数据莫过于平台上公开的消费者在线评论文本,在线评论文本中所隐含的消费者主观情绪会潜移默化的影响后来消费者对产品的态度、对企业的偏好[7],进而影响其风险感知程度[8],这会对电商小微企业的信用产生极大的影响。因此深度挖掘在线评论数据可以有效补充电商小微企业信用相关信息,提升信用风险预警的效果。

本文收集生鲜行业电商小微企业在线评论文本数据,运用LDA法提取在线评论的文本特征,采用情感分析量化电商小微企业信用风险指标,并结合电商小微企业相关的资质指标、经营指标构建契合电商小微企业的信用风险预警指标体系,以此为基础对生鲜行业电商小微企业信用风险进行预警分析。考虑到预警模型的优化,本文将“两步法”优化网格搜索算法与随机森林算法结合搜寻最优参数点,在保证效率的同时构建合理、精准的随机森林模型。

1 主客观两维度信用风险指标体系设计

1.1 理论基础、样本选择、数据来源与处理

本文结合LI和QIAO[9]、CAI等[10]、王冬一等[11]的相关研究,并考虑电商小微企业本身特质,选择最为权威的5C要素理论作为基础,搭建电商小微企业信用风险评级指标体系的框架。研究对象为淘宝平台上C2C生鲜行业小微企业,研究样本来源于淘宝电商平台,使用Python语言编程采集相关数据,于2021年7月31日共爬取1000条店铺数据,经筛选后获得822家样本数据。收集数据后对在线评论文本进行预处理,删除系统自动评论、去除重复评论、人工剔除无关评论、筛去过短无实际分析意义的评论后,共筛选出淘宝生鲜行业店铺822家,获取在线评论33756条。

1.2 电商小微企业信用风险指标体系形成

本文的指标体系分为客观指标和主观指标。指标体系形成的步骤如下:

Step1通过查阅文献、归纳总结,初步获取指标体系中的各指标。

Step2利用Python编码构建LDA主题模型,输出主题、特征词、权重,对LDA主题模型提取的特征词进行分析、归纳、凝练、总结后,得到4个主观指标,分别为产品品质评论情感(A8)、物流包装评价情感(B11)、性价比评价情感(B12)、店铺服务评价情感(C5)。

Step3采用构建情感词典的方式对指标体系中的主观指标进行情感量化。

Step4调用Python中的sklearn包实现随机森林输出特征重要程度,并据此对前文获取的25个指标进行筛选剔除,形成最终的指标体系,筛选后指标体系共有21个二级指标。

基于主客观维度的电商小微企业信用风险预警指标体系见表1。

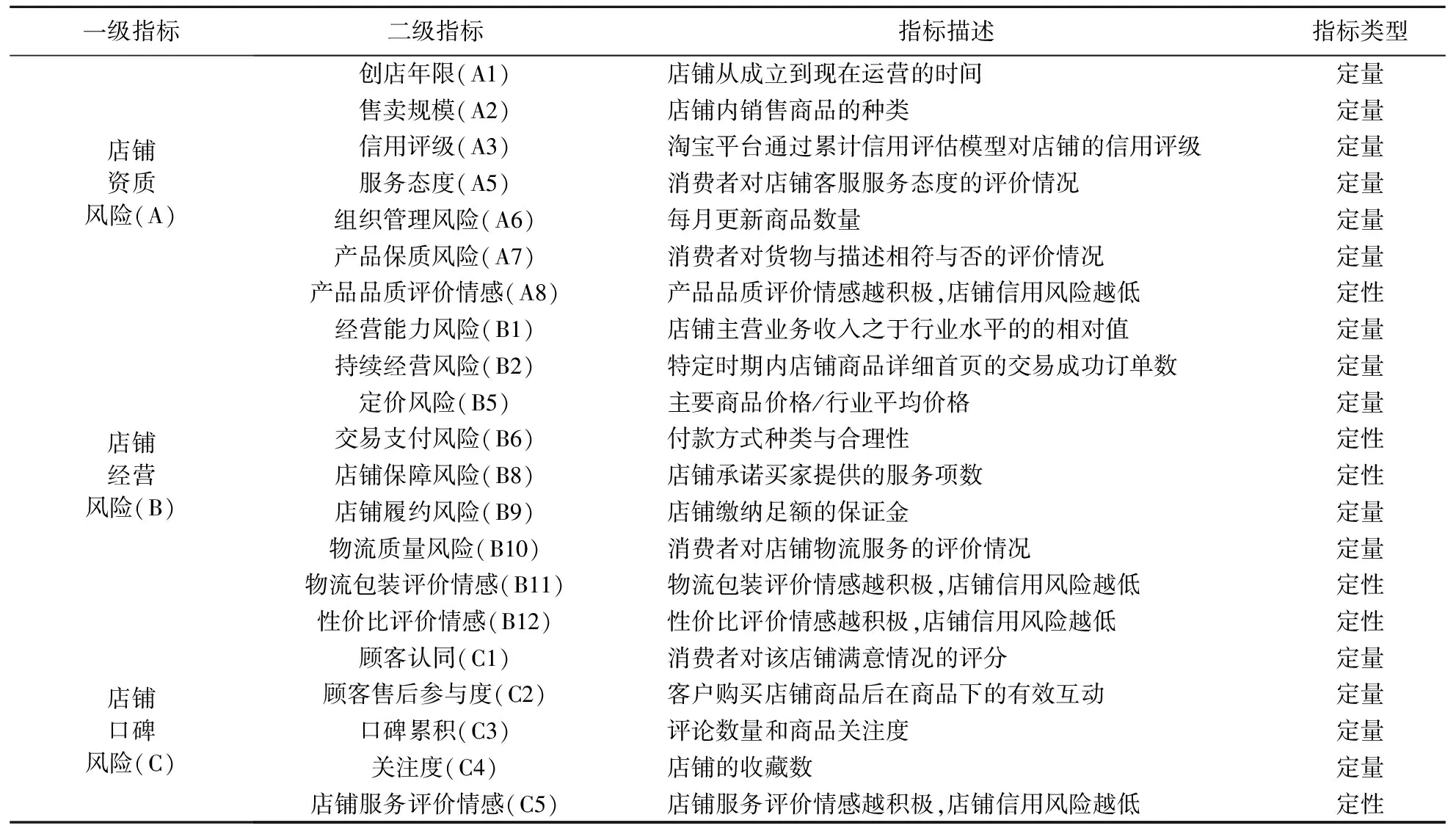
表1 基于主客观维度的电商小微企业信用风险预警指标体系

2 信用风险预警模型设计

2.1 预警阈值确定

将电商小微企业信用风险划分为无风险、轻度风险、中度风险、重度风险4个类别,首先计算RWIt值,公式为:

(1)

其次以正态分布的原理在95%的置信概率下设定风险类别的阈值,作为划分电商小微企业信用风险的分界线,据此设定界定电商小微企业信用风险类别阈值(ηi),设计四段式电商小微企业信用风险程度判定区间。电商小微企业信用风险综合预警指标阈值具体计算公式如下所示,式(2)至式(4)分别表示三个阈值η0,η1,η2。

(2)

(3)

η1=1/2[η2+1/2(η0+η2)]

(4)

若RWIt值小于阈值η2,则说明该企业处于重度信用风险阶段;若RWIt值大于η2小于η1,则定义该企业处于中度信用风险阶段;若RWIt值大于η1小于η0,则定义该企业处于轻度信用风险阶段;若RWIt值大于η0,则定义该企业的信用非常好,无信用风险。

2.2 随机森林预警模型设计与优化

随机森林预警模型的设计与优化步骤如下:

Step1SMOTE算法处理不平衡数据。SMOTE算法的实现公式见式(5)。

xnew=x0+random( )(x0i-x0)

(5)

其中random( )∈[0,1],代表[0,1]内的一个随机数,xnew代表新合成的样本,x0则是代表少数类中的原始样本,x0i代表每次随机选择的x0的第i个最近临近样本。

Step2构建标准RF模型。设由n棵树h1(x),h2(x),…,hn(x)构成一片随机森林,设训练样本集合为D(X,Y),其中X为样本所具有的特征属性,Y为每个样本对应的类别属性。式(6)表示模型正确分类票数超过不正确分类最大票数的程度,该值越大,表明模型的分类效果越好。

(6)

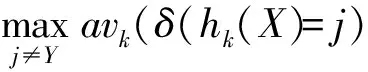
泛化误差的表达式如式(7)所示,其中Px,y表示概率值,PX,Y(mg(X,Y)<0)表示间隔函数小于0的概率,即预测误判概率,泛化误差越低,模型的分类性能越好。

PE*=PX,Y(mg(X,Y)<0)

(7)

随机森林具有收敛性,假设θk,存在随机森林hk(X)=hk(X,θk),当森林中的决策树增加到一定程度后,式(7)将服从强大数定律,序列θk将收敛至式(8),该式说明RF不会因决策树变多而出现过拟合,存在一个有限的泛化误差值。

(8)

(9)

Step3运用“两步法”网格搜索算法优化。第一步在较大范围内划分大网格,通过粗搜索的思想筛选出最优参数可能的范围;第二步在最优范围附近以小步长进行精细搜索,划分出更为密集的网络,在该网络上选择出最优点。

Step4使用最优参数构建RF模型。

3 实证研究

3.1 实证过程分析

本文的实证步骤如下:(1)使用SMOTE和ADASYN两种随机过采样算法进行平衡处理,对比分析处理后构建的标准随机森林模型性能,验证使用SMOTE算法的合理性;(2)对比Logistic模型、CART模型和标准随机森林模型在平衡与非平衡数据集上性能,验证使用平衡数据集的必要性;(3)基于平衡数据集进行模型对照试验,验证随机森林模型的优越性;(4)构建“两步法”网络搜索算法优化随机森林组合预测模型,对标准随机森林模型进行参数优化;(5)随机选取时点和样本进行对比分析,验证预警模型的可推广性和说服力。本部分模型验证时使用最常用的准确率(ACC)、精确率(P)、召回率(R)和F值。

3.2 不同不平衡数据处理方法的比较分析

分别采用SMOTE和ADASYN进行处理,生成平衡数据集,并将得到的平衡数据集按照2:8划分测试集与训练集,对比构建的标准随机森林模型的性能。两种不平衡数据处理方法处理后的数据情况见表2,标准随机森林模型的性能对比见表3。

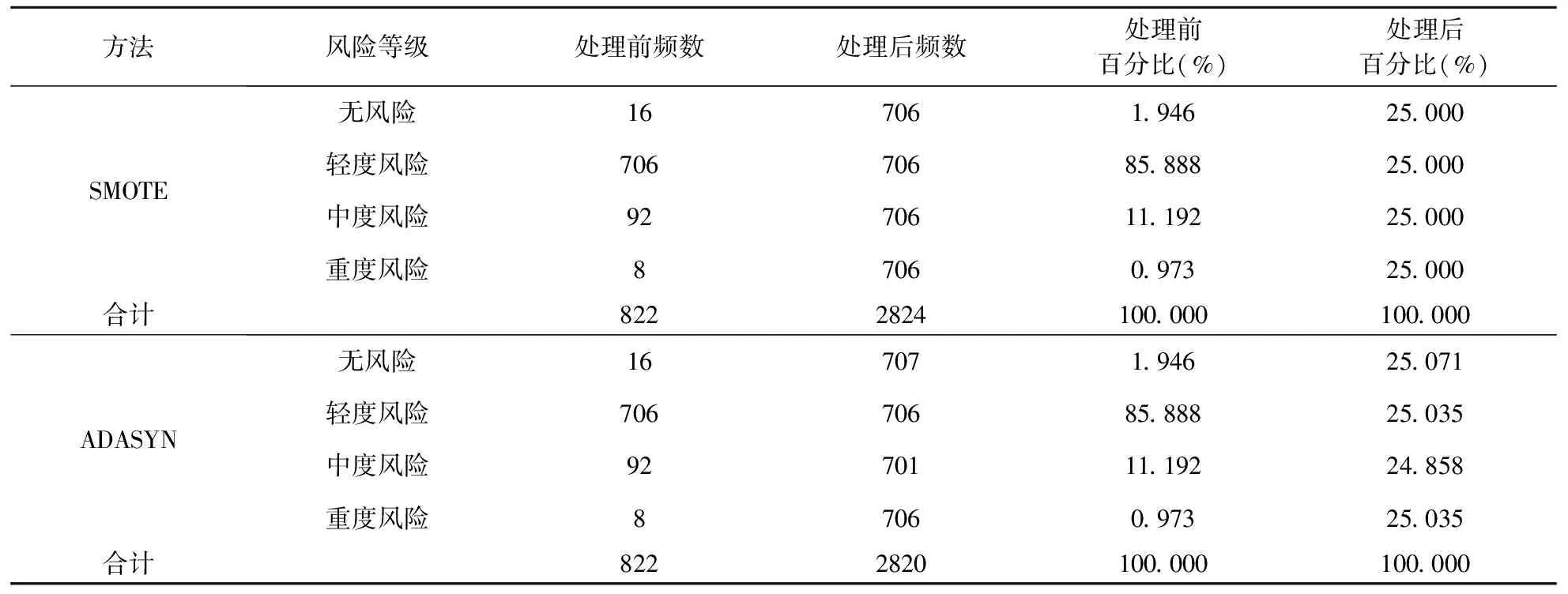
表2 SMOTE和ADASYN平衡处理前后的数据情况

表3 基于SMOTE和ADASYN平衡处理的标准RF模型

表2的结果显示,平衡处理前,无风险、轻度风险、中度风险和重度风险样本分别占总样本的1.946%,85.888%,11.192%和0.973%,分布十分不均衡。处理后的平衡数据集中,四类风险样本各占25%,样本达到平衡。表3的结果显示,基于SMOTE平衡处理后形成的平衡数据集构建的标准随机森林模型,输出的测试集准确率(ACC)、精确率(P)和F值为97.30%,召回率(R)为97.40%。与ADASYN平衡处理后的模型相比性能更高,故本文使用SMOTE算法处理数据集,进行后续的模型构建是合理可行的。

3.3 平衡数据集与非平衡数据集上模型性能比较分析

分别将逻辑回归(Logistic)、决策树(CART)、随机森林(RF)三种预警模型在平衡数据集和非平衡数据集上输出的评估值进行对比,详见表4。

表4 基于非平衡与平衡数据集的模型对比

结果显示,平衡数据集上Logistic模型正确预测电商小微企业风险类别的概率提高了0.87%。而精确率(P)和召回率(R)则出现了极大幅度的变化,探究这种现象产生的根源应从混淆矩阵入手。式(10)和式(11)分别代表非平衡数据集上和平衡数据集上的混淆矩阵,在式(10)的混淆矩阵中,实际为重度风险样本仅有一个,这一样本一旦被错分,会极大幅度拉低整体预测精度,也间接使非平衡数据集输出的精确度和召回率受到较大影响;在平衡数据集输出的混淆矩阵式(11)中,各样本量较均衡,不会出现较为极端的情况,更能如实反映模型真实状态。这也印证了处理不平衡数据集的必要性。

(10)

(11)

对于CART模型,相较于非平衡数据集,平衡数据集上四个指标均达到了百分之九十以上,且优化后的指标整体高于Logistic模型输出的指标,说明决策树易产生局部最优解的特性导致其预测结果并不稳定,受到不平衡数据的影响更大。

对于RF模型,在非平衡数据集中,RF模型的整体准确率(ACC)和精确率(P)明显小于在非平衡样本集中的Logistic模型和CART模型,从混淆矩阵入手寻找产生这种极度差异的原因,在RF模型输出的混淆矩阵中(见式(12)),重度风险类样本仅有一个被划分至测试集,且该样本被误判,这拉低了RF模型整体的精确率(P),致使其表现效果不佳,同样也降低了作为精确率和召回率调和均值F1的输出值。

(12)

通过上述对比进一步分析可知,无论是在单个模型还是在集成模型上,数据平衡与否均会对模型精度产生较大的影响。通过CART模型与RF模型的对比更能说明集成模型在抗干扰性稍优于单个模型,但与之对应的是二者所受数据集不平衡影响均较大,这也印证了如果不考虑样本的平衡性可能会产生较为严重的误判。

3.4 平衡数据集上不同模型性能比较分析

在平衡数据集上验证不同预警模型,首先通过十折交叉验证,可以明显看出RF远优于Logistic和CART。

在平衡数据集上,输出Logistic、CART、标准RF、经参数调优的随机森林四个模型的预测准确率如表5所示。结果显示经参数调优的随机森林模型准确率达到了98%以上。因此调参后的随机森林模型可以更为准确的帮助贷款方辨别电商小微企业所处的信用风险阶段,从而辅助其对是否放贷做出决策。

除此之外,平衡数据集上Logistic模型的召回率为92.67%,CART模型的召回率为94.07%,随机森林模型的召回率为97.9%,调参后的随机森林模型召回率为98.417%,说明在调参后的随机森林模型中,每类预测结果的样本中真正为该类的样本占全部样本的比例较高。也说明了本文的模型具有更高的预测精度。对比标准随机森林模型与调参的随机森林模型输出的指标也以看出,调参后随机森林模型的各个评价指标均优于未调参的随机森林模型。

表5 Logistic、CART、标准RF、经参数调优的随机森林四个模型的预测准确率对比

综合评价指标结果、进行模型对比后发现,调参后的随机森林算法各方面的预测精度均高于其余对照组,即该模型对电商小微企业信用风险的预测最为准确,最能准确判断电商小微企业信用风险所处的阶段,能更好的协助电商小微企业辨别自身信用风险,为贷款机构是否融资提供依据。

3.5 基于“两步法”网格搜索算法的随机森林参数优化

进行参数优化的过程中主要关注tree与features两个参数。考虑到该参数的特性,首先,绘制tree的成长曲线寻找森林中决策子树数量的波动阈值,通过tree成长曲线的初步判断,当森林中决策子树的棵数在(50,200)范围内时,随机森林模型的精度平稳波动,即存在一个最优值确保模型的精度最高,因此可先将该参数的值粗略划分在(50,210)之间。

其次,运用“两步法”网格搜索算法寻找构建森林的最优子树数量。设定森林中决策子树的数量k取值为(50,210),步长设定为20,使得参数在全局寻优的过程中按照大网格进行搜索,输出结果当tree参数为190时,随机森林模型的预测准确率达到97.43%;考虑到大步长设定为20,没有考虑到190前后各20的网格,因此,进一步细化网格步长,设定k的取值为(170,210),步长为10,输出当tree参数为200时,随机森林在测试集上的预测准确率达到97.47%;再次采用“两步法”的思想,进一步缩小参数最优值可能的范围,设定k的取值为(190,210),步长为1,最终输出tree参数为206时,随机森林在测试集上的预测准确率达到最优值97.52%,为进一步验证在(190,210)区间内,tree参数为206时模型最优,绘制随机森林模型泛化误差与森林中决策子树个数的关系图(详见图1),可以看出tree在206,207之间某一点,模型的泛化误差最小,因此本文经过优化后取tree的参数为206,基本上使得随机森林模型精度最大化。

图1 泛化误差与决策子树个数关系

由于参数features取值范围固定,与tree参数有所不同,因此在此对“两步法”思路进行调整,先输出参数features不同取值所对应的模型泛化误差,从整体上观察随机森林模型泛化误差与参数features的关系(输出的关系见图2),可以看出features参数在(5,8)区间内存在泛化误差最小值,但是难以直观确定何处最优,因此运用“两步法”优化的思想,首先设定features的取值为(5,8),设置步长为1,进行全局搜索,最终得到features最优值为6。

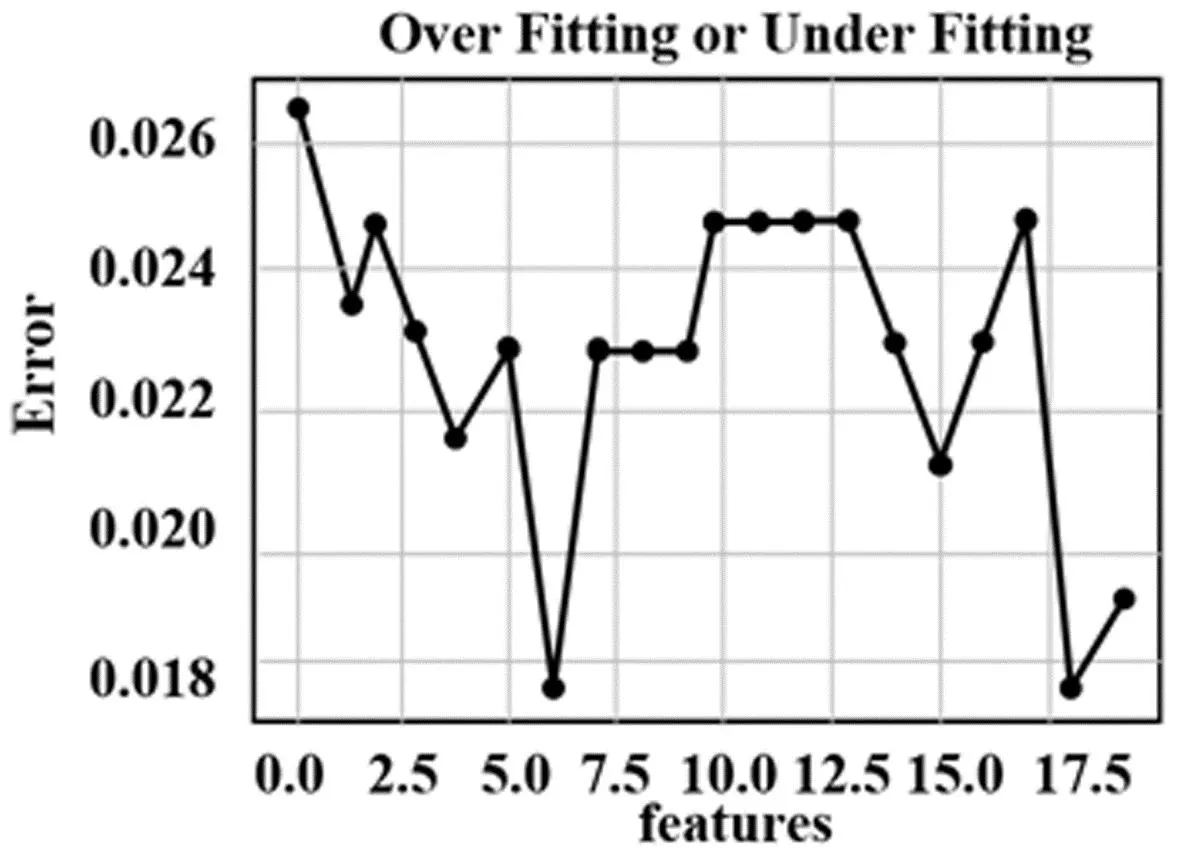
图2 泛化误差与随机选择特征变量个数关系

将tree=206,features=6带入原始标准随机森林模型中,得到模型精度为98.41%,较之原始随机森林模型精度97.88%提升了0.53%的精度,较之仅优化tree参数的随机森林模型提升了0.18%的精度,说明该参数的优化使得模型泛化错误向最低点移动,优化有效。故最终确定建立的随机森林模型中tree=206,features=6。

3.6 不同数据时点平衡数据集上模型结果比较分析

为验证本文构建的电商小微企业信用风险预警模型的可推广性和说服力,本文随机选取2021年7月31日、2021年8月15日、2021年8月30日和2021年9月15日四个时点,随机抽取样本电商小微企业中的40%进行验证。

结果显示,在随机抽取的样本中,不同时点采用本文构建的信用风险预警模型预测的结果均与店铺所属的信用风险预警阈值一致或相近,故从整体来看,本文构建的预警模型是具有可推广性和说服力的。以店铺1和店铺10为例。店铺1的预警阈值是1,表明店铺的起始风险程度是轻风险,随机选取的四个时点的风险预警结果显示,店铺1也属于轻风险范围,说明模型预警结果准确;店铺10的起始风险属于无风险类型,而随机选取的四个时点的风险预警结果中,2021年7月31日依旧为无风险,其余三个时点均为轻风险,表明店铺10的风险水平发生了轻微波动,但波动幅度不大,预测结果与预警阈值的这种差异可能与电商小微企业本身经营不稳定、波动性大有关。