环形路上可分流的多避难点选址模型及算法
2023-02-22马冰玉李红梅罗太波
马冰玉, 李红梅, 罗太波
(1.西北大学 经济管理学院,陕西 西安 710127; 2.西安电子科技大学 经济与管理学院,陕西 西安 710126)
0 引言
近年来,地震、洪水、爆炸等重大突发公共事件频繁发生,造成了严重的人员伤亡。在灾难发生时,为最大限度减少人员伤亡,应使所有避难者在尽量短的时间内完成避难。应急避难点的位置直接影响疏散效率。有效的选址策略不仅需要考虑道路的容量和疏散过程中的堵塞时间成本,还需考虑路网结构特征的影响。已有的应急避难点选址研究大部分集中在路图和树图,而作为大部分城市道路的重要组成部分,环形路目前只受到极少学者的关注。
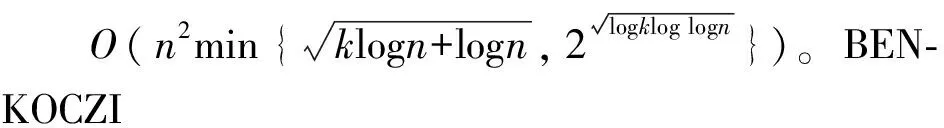
关于环形路上的选址问题目前研究较少,且已有研究都假设同一顶点的避难者只能疏散到相同避难点(即合流模式)。在实际疏散过程中,为提高疏散效率,当某一顶点的避难人数过多时,可能需要将同一顶点的避难者分别疏散到不同避难点。因此,本文基于同一顶点避难者可疏散到不同避难点的假设(即分流模式),考虑道路容量和疏散过程中动态堵塞的影响,研究环形路上k个避难点的选址问题,以最大完成时间最小为目标。
1 问题描述与模型构建
给定一个环形路C=(V,E),其中V={v1,v2,…,vn}为顶点集,假设所有顶点按顺时针方向依次排列;E={e1,e2,…,en}为边集,对任意边ei(1≤i≤n)有ei=(vi,vi+1),特别地,i=n时,en=(vn,v1)。定义l(ei)∈R+为ei的长度;定义w(vi)∈R+为vi的权重,表示位于该顶点的待疏散人数;假设所有的道路容量相同,即单位时间内允许进入ei的最大权重相同,记为c∈R+;定义τ∈R+为环形路上单位权重移动单位距离所需的时间。假设避难点只能落在顶点,本文要求在环形路上确定k(1≤k 记C(vi,vj)为从vi起按顺时针方向到vj的路径,本文称为子环路。对C(vi,vj)任意两点vg,vh,设vg位于vh顺时针方向,记为vh 图1 子环路与虚拟点示意图 性质1以最大完成时间最小为目标,C上权重向避难点疏散时,所有疏散路径都不交叉。 性质2任意给定C(xl,xl+1),划分点有且仅有两种情形: (1)当vg所有权重按逆时针疏散,且vg+1所有权重按顺时针疏散,仅存在两个划分点,即dl,1=vg,dl,2=vg+1; (2)当vg权重同时按顺时针和逆时针疏散,仅有一个划分点,即dl,3=vg。 θ-(xl,xl+1,ul)=max{θ-(xl,xl+1,ul,vh)|vh∈(xl,dl)} (1) (2) θ+(xl,xl+1,ul) =max{θ+(xl,xl+1,ul,vh)|vh∈(dl,xl+1)} (3) (4) 因此,记θ(xl,xl+1,ul)为C(xl,xl+1)按ul的划分分别将权重疏散到xl,xl+1的最大完成时间,简称避难时间,有 θ(xl,xl+1,ul)=max{θ-(xl,xl+1,ul),θ+(xl,xl+1,ul)} (5) x=(x1,x2,…,xk)和u=(u1,u2,…,uk)给定时,记θ(x,u)为C按u的划分将权重疏散到x的避难时间,即 θ(x,u)=max{θ(xl,xl+1,ul)|1≤l≤k} (6) 综上,C上求解k个避难点的选址问题为 (7) 分析上述模型构建过程,将求解C上k个避难点选址问题分解为确定若干个C(xl,xl+1)划分情景的问题,其中1≤l≤k,即通过确定子环路C(xl,xl+1)的最优划分点及相应的最优划分权重,使得C(xl,xl+1)避难时间最小。 给定C(xl,xl+1),记θopt(xl,xl+1)为C(xl,xl+1)的最优避难时间,则有 (8) 引理2给定C(xl,xl+1),θopt(xl,xl+1)存在唯一解。 由引理1和2,可直接得到以下引理。 合流模式中,给定C(xl,xl+1),记φ(xl,vg)为C(xl,vg)的权重按逆时针方向疏散到xl的最大完成时间,有 φ(xl,vg)=max{φ(xl,vg-1)+w(vg)/c,L(xl,vg)τ+w(vg)/c} (9) vg=xl时,φ(xl,vg)=0;记φ(vg+1,xl+1)为C(vg+1,xl+1)的权重按顺时针方向疏散到xl+1的最大完成时间,有 φ(vg+1,xl+1)=max{φ(vg+2,xl+1)+w(vg+1)/c,L(vg+1,xl+1)τ+w(vg+1)/c} (10) vg+1=xl+1时,φ(vg+1,xl+1)=0。记φopt(xl,xl+1)为C(xl,xl+1)最优避难时间,则 (11) (12) 根据上式可得如下关于最优解性质。 性质4给定C(xl,xl+1),设α*为公式(12)中α的解,则 根据以上引理和性质,求解C(xl,xl+1)划分情景的确定问题有求解算法A1: 步骤1不妨令xl=vp,xl+1=vq,在合流模式下,令vg按顺时针顺序依次取vp,vp+1,…,vq-1,计算φ(xl,vg);并令vg按逆时针顺序依次取vq,vq-1,…,vp+1,计算φ(vg,xl+1)。 定理1根据算法A1,C(xl,xl+1)上划分情景的确定问题可在O(n)内求解。 在求解C上k个避难点的选址问题时,若k=1,可在算法A1的基础上进行求解;若k>1,可设计动态规划算法进行求解。当k=1时,由于避难点只位于顶点上,所以x的位置最多存在n种可能。通过比较每一种可能下的避难时间,选择最小值为C的最优避难时间,最小值对应顶点为最优避难点。 定理2环路C上1个避难点的选址问题可在O(n2)时间内求解。 (13) 递推公式的边界条件表示为: (14) 步骤1令xl和xl+1为C上任意一点,根据算法A1,计算求得所有C(xl,xl+1)的最优划分情景和最优避难时间。 定理3根据算法A2,环路C上k(k>1)个避难点的选址问题可在O(kn3)时间求解。 首先随机生成一个环形路,给出相应的计算过程展示算法A2的关键步骤;之后在不同的k值下,比较合流与分流模式对最大疏散完成时间的影响。 给定C=(V,E),如图3所示。图中内圈数字表示对应顶点权重w(vi),外圈数字表示对应边的路长l(ei);假设道路容量c=1,通行速度τ=1。在分流模式下,要求在环形路上确定5个避难点位置,使最大疏散完成时间最小。 图3 环形路示意图 图4 环形路最优解示意图 在这部分算例中,针对不同的k(1~10)值,分别计算合流模式与分流模式对应的最优选址方案以及最大完成时间。结果表明对于任意的避难点数量k,分流模式下的最大疏散完成时间都优于合流模式下的最大疏散完成时间。与合流模式相比,当避难点数量较少时,能被划分的点也相对较少,因此改进的效果有限;同样,当避难点数量较多时,由于大部分权重较大的点被选做避难点,导致划分点的权重较小,因此改进的效果也相对较小;而当避难点的数量适中时,也即在算例中避难点数量为6,7,8时,分流所带来的效率提升最为显著。 统计在10次试验中所有顶点被选为避难点或划分点的次数后发现,在所有的最优选址方案中,大部分权重较大的顶点被选为避难点,或者其权重被划分去往不同的避难点。顶点v13被选为避难点的次数最多,达到7次,其次是v10(6次)和v6(5次);其中v13的权重是所有顶点权重中最大的。被选为划分点次数最多的是v4,v7和v12,均达到5次。由于最大疏散完成时间受到所有顶点权重分布情况以及道路情况的综合影响,通过顶点权重分布与顶点被选为避难点次数和顶点被选为划分点次数的折线关系图可知,避难点选择过程中对权重更大的顶点有比较一致的倾向性,即存在顶点权重越大该顶点被选为避难点的次数越多这一趋势,但这个倾向性在划分点的选择过程中并不具备。 已有的应急避难点选址问题相关研究多假设同一顶点的避难者只能经由相同的疏散路径疏散到相同的避难点,而该假设会影响实际中的疏散效率。本文放宽该假设,允许同一顶点的避难者经不同路径疏散到不同避难点,考虑道路容量和疏散过程中的堵塞成本,研究了环形路上的k-避难点选址问题。通过将环形路上的选址问题等价为有限个路径上的选址问题,并结合动态规划思想,本文给出了时间复杂度为O(kn3)的求解算法。进一步通过数值分析可知,由于分流模式能够把权重较大顶点对应的避难者派往不同的避难点,因此相较于合流模式,分流模式能够有效的提高疏散效率。相关的理论模型和算法为实际中的避难点规划提供了一定的理论指导。在灾害发生时,由于各个顶点的人数很难准确获得,后期的研究将考虑权重不确定的鲁棒优化模型。
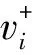
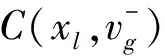
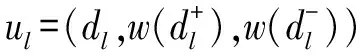






2 子环路C(xl,xl+1)划分情景的确定
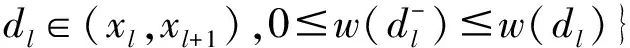

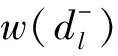
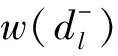
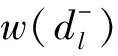
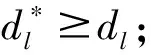
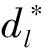
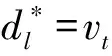


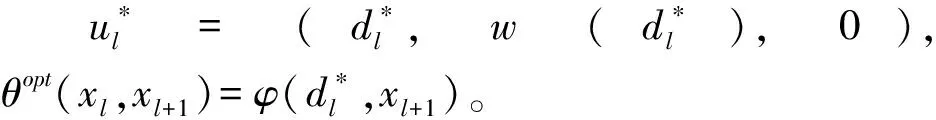
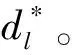
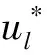
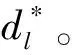
3 k个避难点选址问题的算法设计
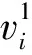

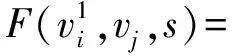
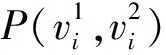
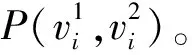
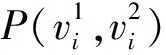
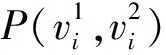
4 数值算例
4.1 算法求解示例

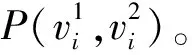
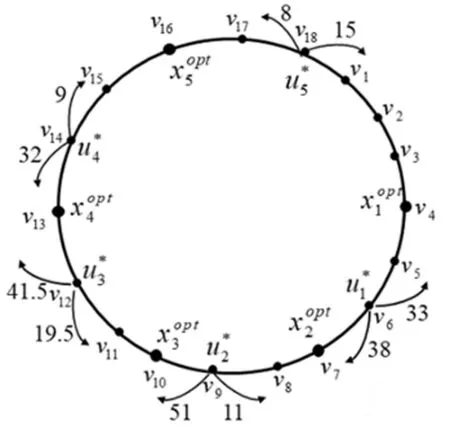
4.2 合流与分流模式的对比分析
5 结论
