基于灵敏度分析的转向架构架有限元模型修正

刘乐天， 李凡松， 宋 烨， 刘潮涛, 邬平波

(西南交通大学 牵引动力国家重点实验室,成都 610031)

构架是轨道车辆转向架非常重要的部件之一，起承重、减振、传力等作用，同时受到轮轨、车体以及吊挂设备等所产生的激振力[1]。目前，运营列车中存在很多由于线路激励与构架模态产生共振而引发的构架开裂问题[2-8]，大量线路试验数据表明，多数情况下，线路激励频率是确定的，因而转向架构架模态参数的准确度对于研究此种开裂问题和转向架后期优化变得十分重要，构架的模态试验可以获得准确的模态参数，开展相关研究需要同样准确的有限元模型，如何获得一个准确的构架有限元模型成为了一个受到普遍关注的问题。

有限元模型修正方法包括灵敏度分析法，粒子群算法，元启发式算法和神经网络算法等，灵敏度分析法相比于其他具有随机性的算法更加高效合理，因而灵敏度分析算法是最为常用的模型修正方法之一[9-13]，国内外学者已经对模型修正方法进行了大量研究。李凡松[14]基于粒子群法对整备状态动车组车体模型进行了修正；Hofmeister等[15]基于元启发式算法提出了一种新的无导数全局优化方法，基于该算法对风力涡轮机中的转子叶片进行了模型修正;Mottershead等[16]对敏感度方法计算的重要步骤进行了基本介绍，并利用直升飞机机身模型修正对其理论进行了验证；邱飞力等[17]利用参数扰动比改进了模态灵敏度，采用模型修正的正则化算法完成了某铝合金车体的模型修正；张淼[18]给出了灵敏度矩阵修正法求解模型的数学方法，同时归纳了其模型修正的一般步骤；张权等[19]采用二次规划算法并在此基础上研究了加权方法在模型修正上的应用。

构架的结构虽然较为简单，但由于制造工艺的局限性和焊缝对材料刚度的贡献，根据设计模型所建立的有限元模型与实际制造的构架难免有误差，对于精准的振动模态计算具有很大影响。目前模型修正研究仅考虑了构架的局部板厚的建模误差对模态参数造成的影响[20]，但还未有人对构架焊缝刚度的建模误差产生的影响进行相关研究。本文基于灵敏度分析对转向架构架有限元模型进行修正，同时考虑构架板材厚度加工公差[21]和焊缝对材料刚度的贡献两方面因素，通过对比模态频率相对误差和MAC(modal assurance criterion)值进行验证，证明该方法可以为后续的仿真计算提供准确的有限元模型，并对转向架的结构设计和参数选择等方面具有一定的参考价值。

1 模型修正理论

在模型修正中，待修正参数是在模型的设计参数中选取的，可以是材料属性，几何参数或边界条件等。当改变原始模型的待修正参数p=(p1,p2,…,pn)时，模型的模态参数、模态的MAC即模态置信准则，用于检查两阶模态之间的相互独立性和一致性、质量或刚度矩阵等修正对象f会随之改变。因此可以将修正对象f视为待修正参数p的函数，记作f(p)。为了将问题线性化，在初始位置p0处，将f(p)进行一阶泰勒展开

(1)

式中：Δp为待修正参数的变化量；p0为待修正参数的初始值。

灵敏度矩阵为

(2)

式中:m为修正对象的数量；n为待修正参数的数量。

式(1)可写成

f(p)=f(p0)+SΔp

(3)

模型修正的目的是使修正对象与试验结果的误差达到最小，同时待修正参数仍具有物理意义，需给定待修正参数合理的取值范围，故设置目标函数为

(4)

s.t.pmin≤p≤pmax

式中:fe(p)和fm(p)分别为修正对象的仿真值和试验值；pmin为待修正参数取值范围的最小值；pmax为待修正参数取值范围的最大值。

结合式(3)和式(4)，利用拉格朗日数乘法得

ΔR=SΔp=fe(p)-fm(p0)

(5)

根据式(5)设计参数的变化量可写为

Δp=S-1ΔR

(6)

但在多数情况下，灵敏度矩阵的秩l不等于待修正参数的个数n，当l>n时，引入广义逆矩阵求解得

Δp=(STS)-1STΔR

(7)

当l>n时，引入广义逆矩阵求解得

Δp=ST(STS)-1ΔR

(8)

待修正参数的类型不同时，很难比较灵敏度的大小，这种情况下灵敏度矩阵极易出现病态，所以灵敏度矩阵需要进行归一化处理，则

(9)

归一化后Δp需变换为

(10)

为了使迭代计算更加高效准确，分别对待修正参数的变化量Δp和修正对象的误差ΔR进行加权处理，目标函数变为

minJ(Δp)=λ2ΔpTWpΔp+ΔRTWeΔR

(11)

s.t. Δpmin≤Δp≤Δpmax

式中:Wp和We分别为Δp和ΔR的加权矩阵；Δpmin和Δpmax分别为待修正参数修正量的最小值和最大值。

若修正对象为模态频率和模态振型MAC值，We可表示为

(12)

式中，Wf和WMAC分别为模态频率和模态振型MAC值的加权系数。

Wp可表示为

(13)

Г=diag[STWeS]

(14)

Δp=(STWeS+λ2Wp)STWeΔR

(15)

式中，λ2为加权系数，建议λ2的值取0～0.3，当待修正参数灵敏度不高的数量越多或STWeS条件数越大时，λ2取值越大。

通过式(15)求解出Δpk，获得新的待修正参数pk+1，用pk+1替换旧的待修正参数pk，获得新的有限元模型进行迭代计算。

pk+1=pk+Δpk

(16)

2 转向架构架模态试验

2.1 试验方法

构架共选取42个测点，其中侧梁、横梁和纵梁分别选取24个、16个和2个，测点分布如图1所示。

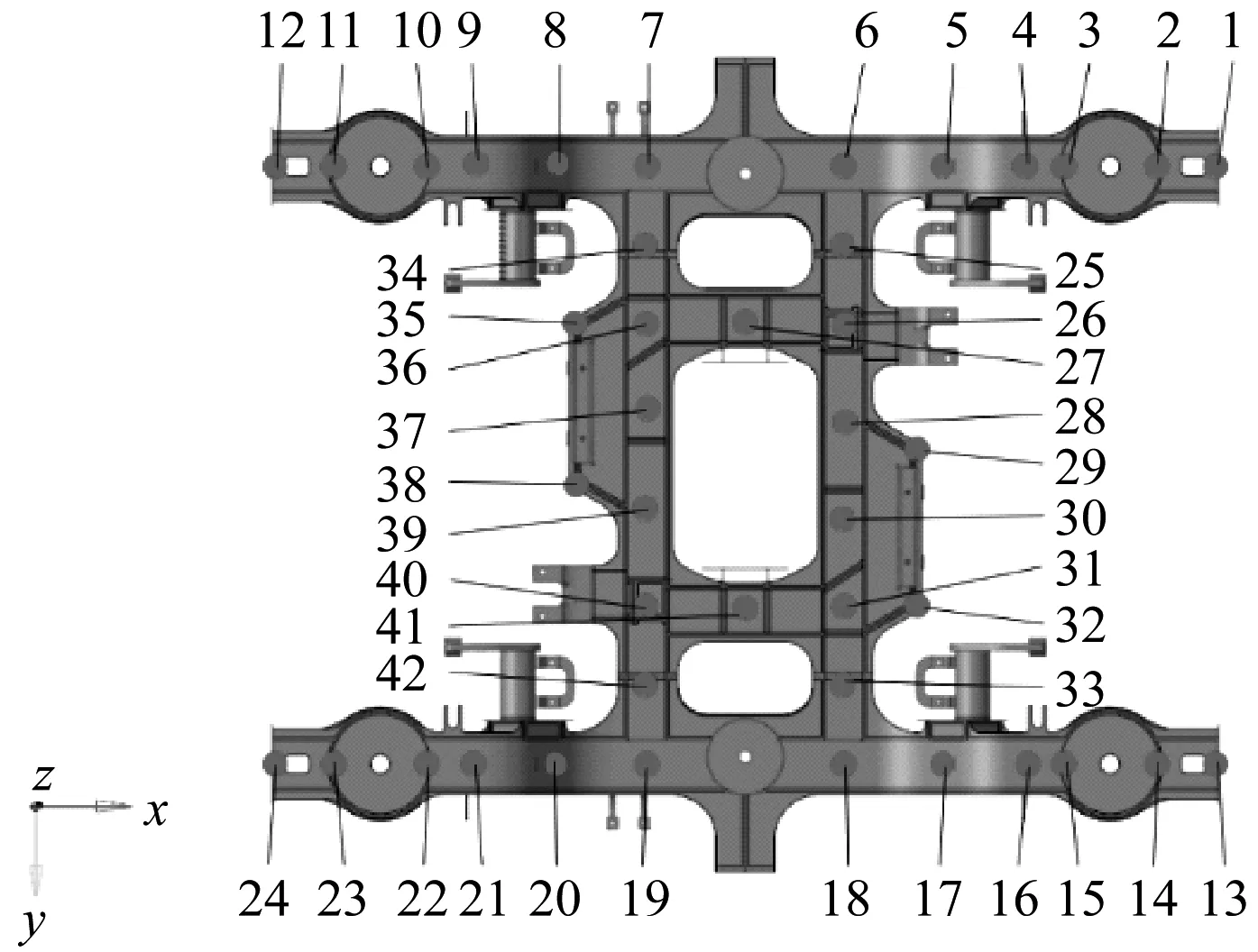
图1 构架测点分布图

构架采用钢簧支撑，分别支撑在4个转臂节点座处，弹簧刚度为300 kN/m，构架质量为1.9 t，所以构架支撑频率为4 Hz，小于构架第一阶模态频率的1/10[22]。采用激振器扫频激振法，使用激振器多次扫频，每两次扫频移动传感器的位置以完成所有测点的测量，如图2所示。激振器扫频范围为0.1～200.0 Hz，采用三向5g加速度传感器，采样频率为2 000 Hz。

图2 构架模态测试照片

2.2 数据处理

利用LMS Test.Lab中的Polymax模态识别程序对构架模态试验数据进行分析，模态频率识别结果如表1所示，前6阶模态振型如图3所示。

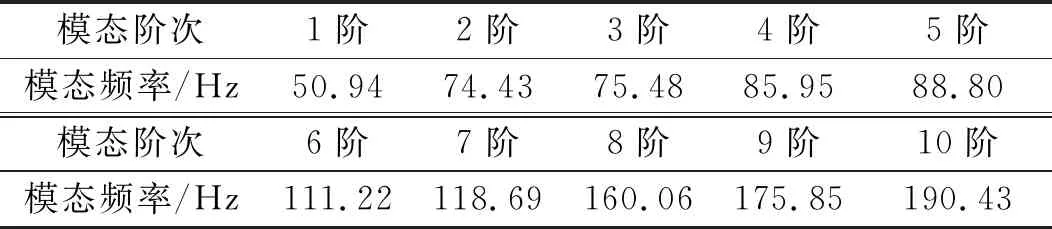
表1 构架模态试验频率

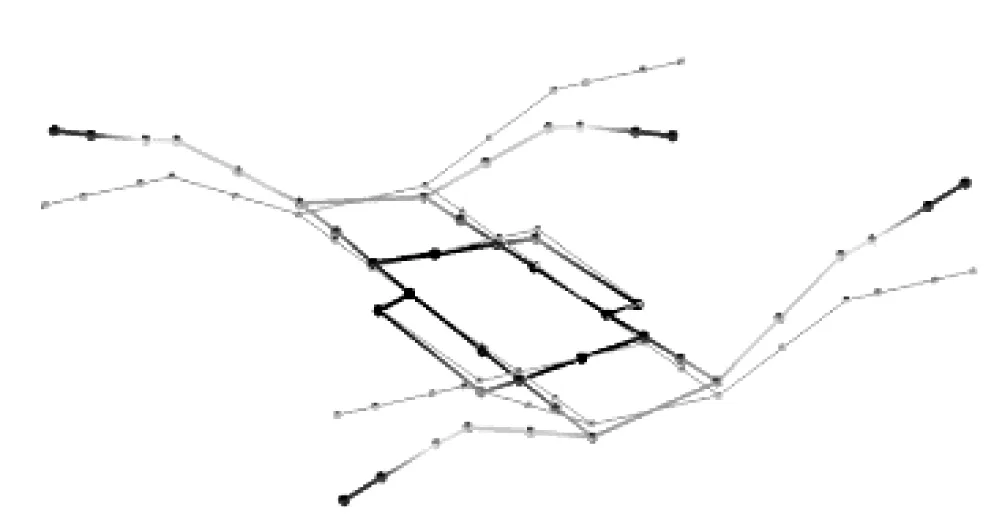
(a) 1阶模态振型图

3 仿真计算

3.1 有限元模型建立

构架为H型全钢焊接结构，主要由侧梁、横梁以及各部件安装座组焊而成。故有限元模型的建立以壳单元为主，四面体单元为辅，单元的基本尺寸为10 mm。构架共划分单元347 810个，节点数为207 468个。构架主体结构采用壳单元进行划分，单元类型为shell181，制动吊座，电机安装座和齿轮箱安装座等结构采用四面体单元进行划分，单元类型为solid185。构架有限元模型,如图4所示。

图4 构架有限元模型

有限元模型对构架焊缝进行简化处理，并未画出实际焊缝，为了避免焊缝本身存在的质量对构架模态计算精度产生影响，对焊缝位置的壳单元进行单独分组，实际焊缝示意图，如图5(a)所示;有限元壳单元侧视图，如图5(b)所示。A,B部分分别为两薄板壳单元焊缝壳单元分组，根据实际板材的坡口尺寸确定实际焊缝质量，通过改变A,B部分壳单元的密度将焊缝的质量均分到两板材交界处，实现焊缝质量等效。

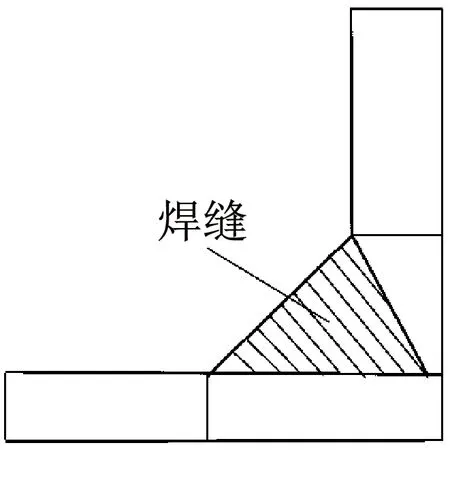
(a)

实际中，质量良好的焊缝可以增加一定的结构刚度，但往往很难保证所有焊缝的质量，导致焊缝质量下降的因素很多，如单边焊时未熔透，焊接表面有杂质和焊接环境湿度过大等，都会使焊缝质量下降，导致焊缝的等效弹性模量减小。因此，为了便于后面对焊缝等效弹性模量进行修正，焊缝等效弹性模量初值选取2.1×105MPa(与母材一致)。

3.2 模态对比

有限元模型计算出的构架模态需要与试验结果进行对比，频率误差和模态振型误差是两个重要的评价指标，频率误差采用频率相对误差R表示，如式(17)所示，而以向量形式表达的模态振型的误差很难以直观的方式计算，所以模态振型使用向量对比的方法来评判两种振型的相似度，其中MAC计算是最为常用的方法之一，MAC计算可用式(18)表示。当MAC值为1时，代表振型完全一致；当MAC值为0时代表两个向量正交，即两个完全不同的振型。

(17)

(18)

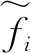
利用ABAQUS软件对构架的有限元模型进行模态分析，初始有限元模型的模态分析结果和试验结果的对比情况,如表2所示。

根据表2知，有限元模态分析的前10阶模态最大频率误差为3.34%，最小MAC值为0.852。可以看出仿真结果各阶振型与试验结果相似度较高，而模态频率有较大误差。

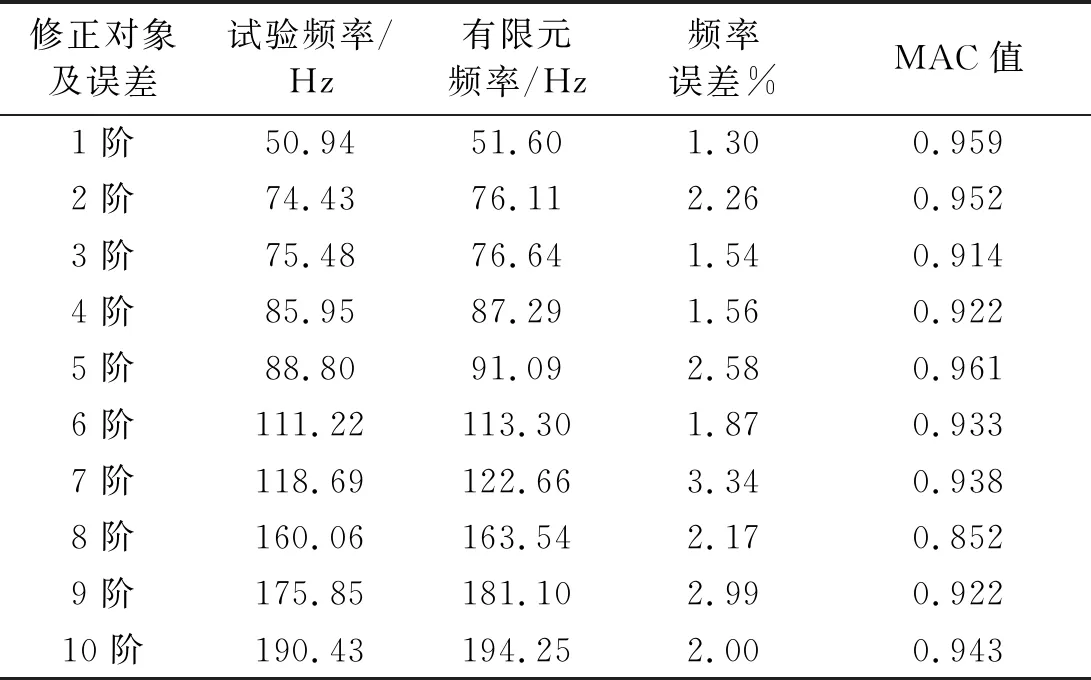
表2 模态对比结果

4 转向架构架有限元模型修正

构架结构较为简单，主体结构是由钢板焊接而成，故主要误差来自于有限元模型对焊缝的简化和钢板厚度的理想化。实际上，焊缝不但影响构架的质量还会影响其刚度，根据GB/T 709—2019《热轧钢板和钢带的尺寸、外形、重量及允许偏差》知，钢板由于加工精度的不足，构架所用钢板厚度公差最大能达到±1 mm，也会影响构架的模态参数。焊缝对构架质量的影响已在有限元建模的过程中考虑到，故在修正时，选取焊缝区等效弹性模量和厚度为10 mm,12 mm,14 mm和18 mm主体结构钢板厚度作为待修正参数。为了保证在修正模态频率同时，模态振型也有较高的相似度，故选取前6阶模态的频率和MAC值作为修正对象，对初始有限元模型进行修正。

取Wf=1，WMAC=0.2，λ2=0，则目标函数为

minJ(Δp)=ΔRTWeΔR

一般要求关注的模态频率误差小于2%，MAC值高于0.9，利用第1章论述的修正理论进行5次迭代，模态频率收敛过程如图6所示;MAC值收敛过程如图7所示;模型修正后的模态频率和MAC值与试验数值对比如表3所示;修正参数修正结果如表4所示。

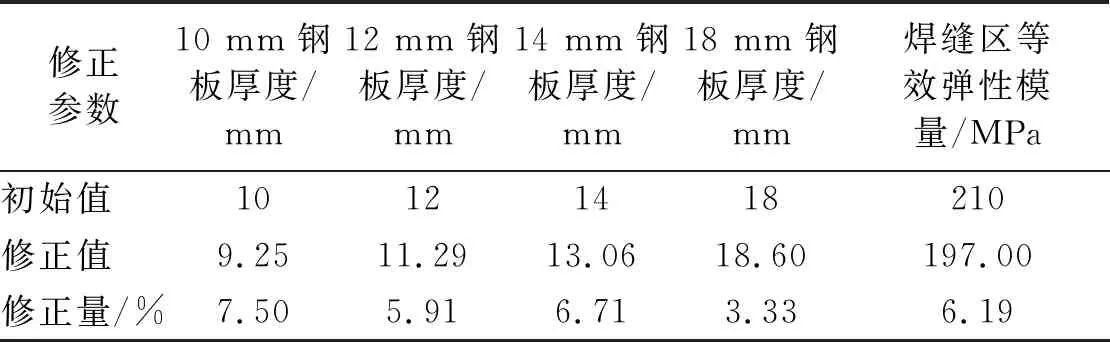
表4 修正参数修正结果

图6 前6阶模态频率收敛图

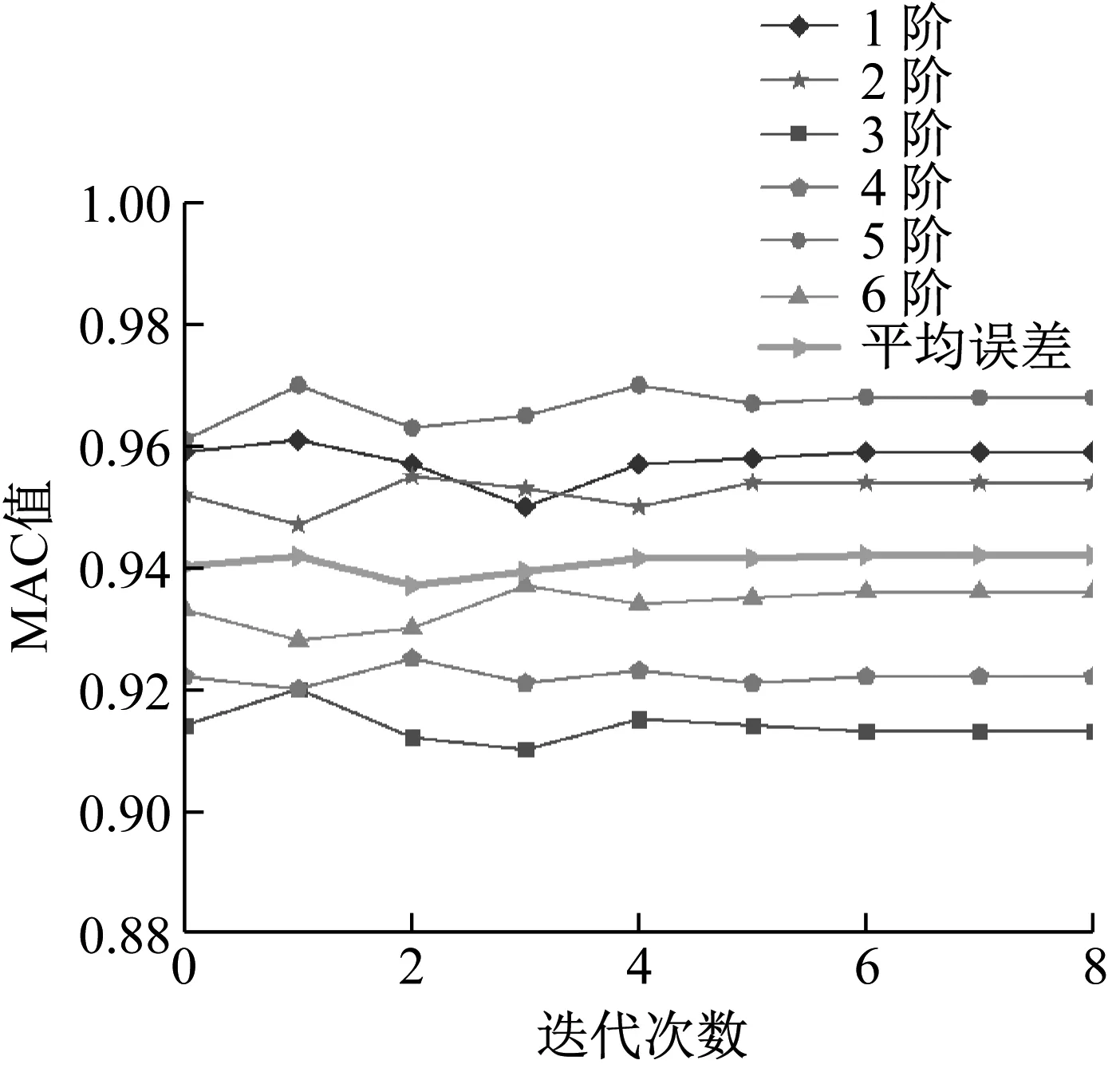
图7 前6阶MAC值收敛图

由表3可知:构架模型修正前，前6阶模态频率平均误差为1.85%，最大误差为2.58%;前6阶MAC值平均值为0.940，MAC值最小值为0.914。构架模型修正后，前6阶模态频率平均误差为0.59%，最大误差为1.22%，6阶MAC值平均值为0.942，MAC值最小值为0.915，满足修正精度要求。

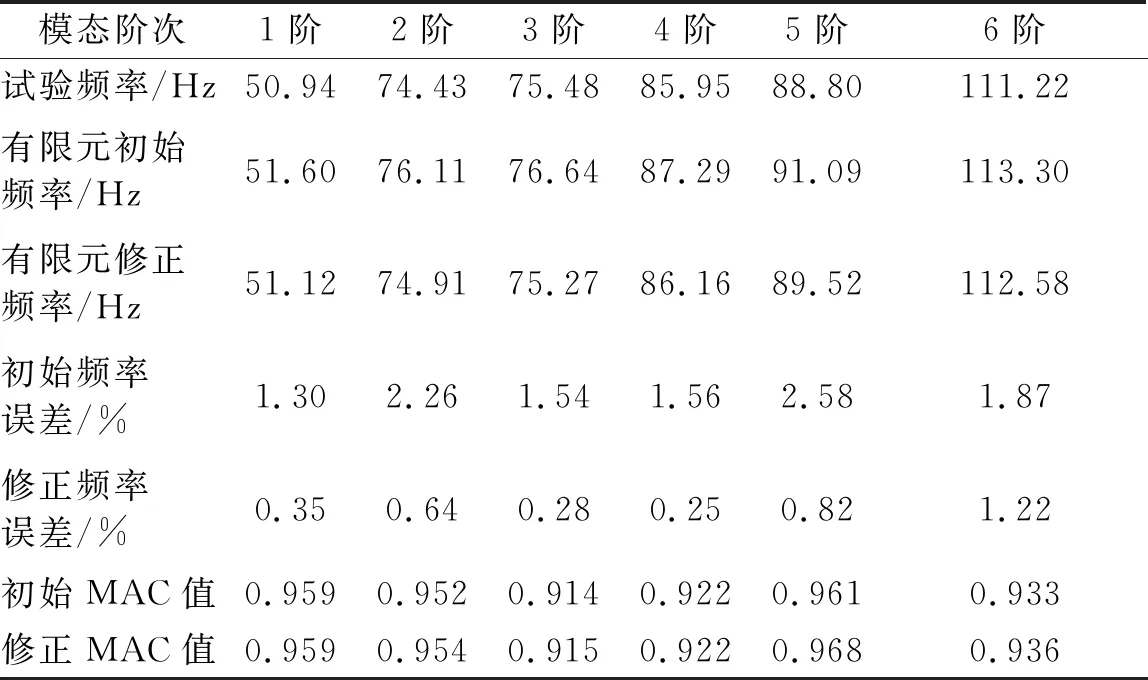
表3 模态频率和MAC值修正结果对比

根据修正结果可以看出，经过模型修正模态频率误差有了很大程度的减小，而MAC值与初始模型的平均值仅相差0.002，没有明显变化，模态振型仍保持较高的相似度，板材厚度修正量在规定公差范围内，而焊缝区等效弹性模量有所下降，在实际结构中存在很多单边焊的焊缝，很容易出现未熔透的情况，导致焊缝区等效弹性模量下降，且下降量在合理变化范围内。因此，修正后的构架模型达到了预期的修正结果。

5 讨 论

同时修正模态频率和MAC值模态频率的相对误差明显减小，而MAC值基本不变，说明修正板厚和焊缝区等效弹性模量对模态振型影响甚微。那么考虑只修正模态频率而不修正MAC值的方法是否可行，下面进行如下验证，将修正对象改为模态频率，有限元模型输出结果仍为模态频率和MAC值，验证结果如表5和表6所示。

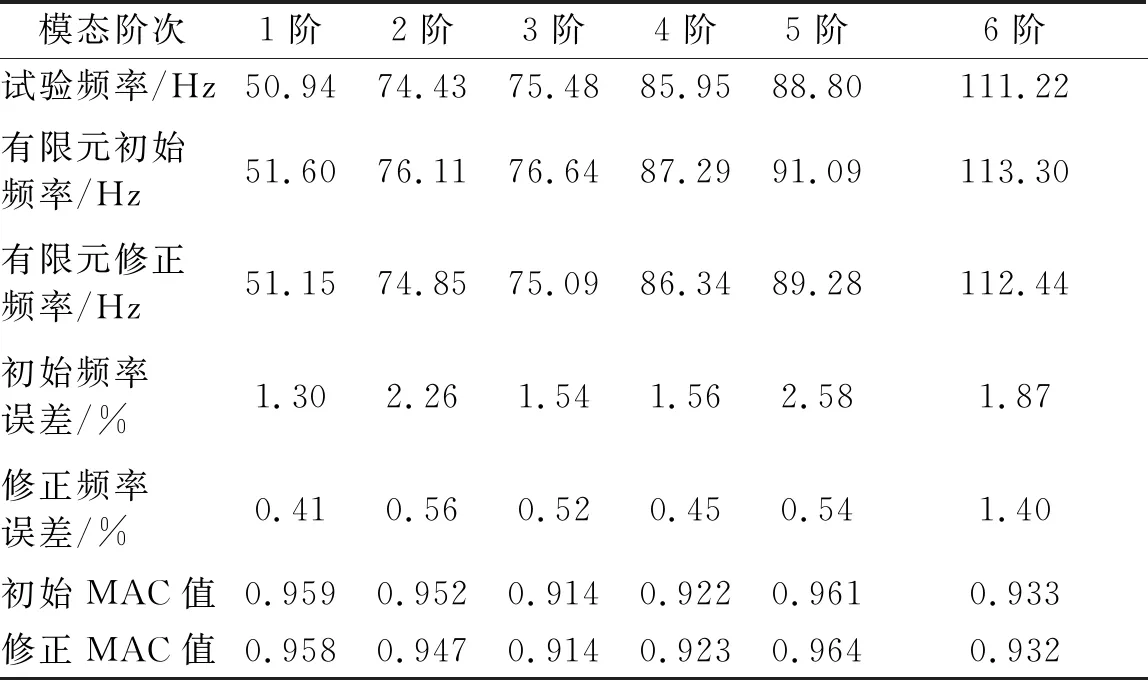
表5 仅修正模态频率结果对比

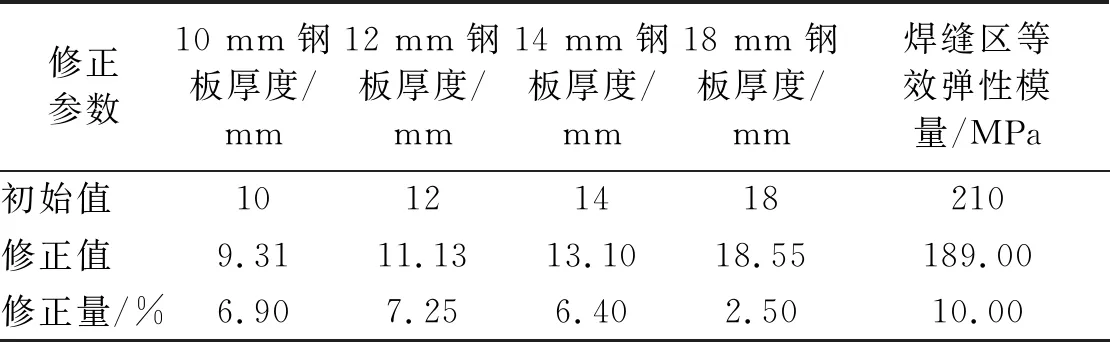
表6 修正参数修正结果

由表5可知，采用仅修正模态频率的方法修正后，前6阶模态频率平均误差为0.65%，最大误差为1.40%，6阶MAC值平均值为0.940，MAC值最小值为0.914，满足修正精度要求。

经验证发现，通过同样的模型修正方法，将修正对象由模态频率和MAC值变为模态频率依然能达到同样的修正效果。因此，建议进行构架模型修正时，修正对象目标可以仅考虑模态频率。

6 结 论

以转向架构架的模态试验数据为基准，基于灵敏度分析法对构架有限元模型的必要参数进行修正，得出如下结论：

(1) 对灵敏度矩阵加权法在有限元模型修正方面进行研究，通过激振器扫频法获得构架试验模态，建立考虑焊缝质量影响的构架有限元模型，使用该模型结合模态试验数据验证了灵敏度矩阵加权法在有限元模型修正中的可行性。

(2) 以转向架构架的模态试验数据为基准，采用灵敏度分析法对转向架构架的主要板材厚度和焊缝区等效弹性模量进行修正，修正后的模态频率和模态试验结果基本一致，且修正参数均在合理取值范围内，模型可以为开展有关构架模态共振产生的开裂问题与后期优化设计提供基础。

(3) 从修正参数修正结果可以看出，构架主要板材厚度变化量在公差范围内，是由于钢材加工精度导致的，焊缝区等效弹性模量降低是由于部分焊缝未熔透所导致。

(4) 同时修正模态频率和MAC值的结果表明构架模型修正对MAC值影响极小，采用仅修正模态频率而不修正MAC的方法验证发现，仅修正模态频率同样可以到达预期效果，提出构架模型修正可仅考虑修正模态频率的建议。