曲梁缓冲器的大变形及变形能的椭圆函数解

2023-02-22霍银磊裴学胜李梦瑶

振动与冲击 2023年3期

霍银磊，裴学胜，李梦瑶

(1. 河南科技大学艺术与设计学院，洛阳 471000； 2. 河南科技大学工业设计中心，洛阳 471000)

随着“双碳”目标的提出，符合现代绿色环保要求又具有良好缓冲特性的轻质吸能材料或结构得到航空工业、机械工业以及物流行业的广泛关注。金属材料即使在有限或大的变形情况下仍然具有良好的回弹性，能够克服植物纤维回弹性差[1]的问题，被越来越多的应用于缓冲防震系统，如弹簧。但简单的弹簧系统一般具有线性变形特征，不具备泡沫塑料及纤维类结构材料等传统缓冲材料的几乎恒力的变形阶段(平台应力区)，对冲击能量的吸收能力较差。然而，特定形状的金属结构件却可能存在恒力变形阶段，例如：Pham等[2]曾利用曲梁设计了一个可在区间内输出恒力的恒力多稳态机构，并将此机构用于系统的过载保护。类似的，学者对曲梁的振动问题研究较多：例如准零刚度隔振器[3-5]，曲梁周期结构隔振器[6]，平面拱的振动问题[7]等。松田技术研究所[8]基于曲梁开发了用于大型精密仪器运输减震的金属球状减震器，其试验结果表明减震器能实现98.5%的减震效果。但上述研究没有涉及到对其大变形及冲击能量吸收特性的理论或者试验分析。

此外，学者们很早就开始将椭圆积分和椭圆函数理论用于梁的大变形问题的分析，Born[9]于1906年首次使用椭圆积分对悬臂梁的后屈曲平衡构型进行试验理论研究。21世纪初，Howell[10]在其著作中对柔顺机构的分析和设计方法进行了详细的回顾，给出了许多利用椭圆积分分析的例子。Kimball等[11]利用椭圆积分求解悬臂梁在端部力及力矩作用下的大挠度的Bernoulli-Euler梁方程，对梁的拐点存在条件及末端挠度进行了分析，分别给出了悬臂梁在纯弯矩载荷、纯力载荷、以及力和弯矩同时加载情况下的椭圆积分解。Zakharov等[12]研究了不同固定条件和末端静载下细杆非线性弯曲问题，给出了弹性细杆的椭圆函数精确解；随后，Zakharov等[13]又研究了末端随从力作用下细杆的非线性弯曲问题，给出了任意角度随从力作用下细杆的雅可比椭圆函数解，指出其挠度取决于由力的大小和斜率以及解的模式决定的椭圆模量。Levyakov等[14]以点载荷作用下的杆和圆环结构为例研究了杆件(包括悬臂)屈曲后平衡状态的稳定性，并在讨论中使用了Jacobi椭圆函数解。Batista[15]给出了自由端受到力矩和倾斜力作用的悬臂直梁的Jacobi椭圆函数解，详细讨论了悬臂梁可能的平衡形状。乌榕江[16]引入了梁的轴向变形建立了更完整的悬臂梁平面大挠度变形的组合数学模型，运用椭圆函数的方法研究了悬臂梁的平面大挠度变形问题。近些年，一些学者还研究了固定-导向柔顺梁的椭圆积分解：Holst等[17]用椭圆积分建立了梁的弯曲模型，研究了柔性机构中固定导向梁的挠度和屈曲问题。张爱梅[18]基于Bernoulli-Euler梁理论，通过引入表示拐点个数的变量以及表示弯矩方向的参数，得到了大挠度梁的完备椭圆积分解，该完备解可用来求解任意拐点数的变形以及各种末端载荷情况的细长梁变形形态。

以上研究主要针对悬臂直梁，针对曲梁的分析较少，Lin等[19-21]分别利用拉格朗日和欧拉描述分析了层合曲梁的有限变形，分给出了圆曲线和螺旋曲线层合梁的解析解，其在半圆曲梁大变形分析中利用了椭圆积分的思想。本文针对两端固支的曲梁结构缓冲器，考虑压力作用下曲梁的大变形特性，基于Euler-Bernoulli梁理论建立曲梁的大变形平衡方程，运用椭圆函数的知识求解悬臂梁的大变形问题，并分析端部固支的曲梁球形缓冲结构发生大变形时的位形及能量吸收特性。

1 大变形曲梁的一般平衡方程

考虑如图1(a)所示的球形曲梁结构缓冲器，位于上下两压板间的缓冲器初始高度为H。组成缓冲器的单根曲梁如图1(b)所示，两端固支的圆形曲梁截面厚度t，宽度b，安装端初始截面角为αL，曲梁在竖直外力F作用下发生弯曲变形，变形后缓冲器高度为h。

(a) 球形减震器

对于两端固支曲梁，考虑曲梁变形的对称性，可知曲梁轴线中点p0所在横截面始终垂直于y轴。取其一半作为对象进行研究，以p0点为原点建立浮动坐标系xoy，曲梁轴线上任意点p的曲线坐标为s，以α∈(0,αL),θ∈(0,αL)表示变形前后p处轴线切向与y轴的夹角，曲梁变形前后的受力及变形情况如图2所示。

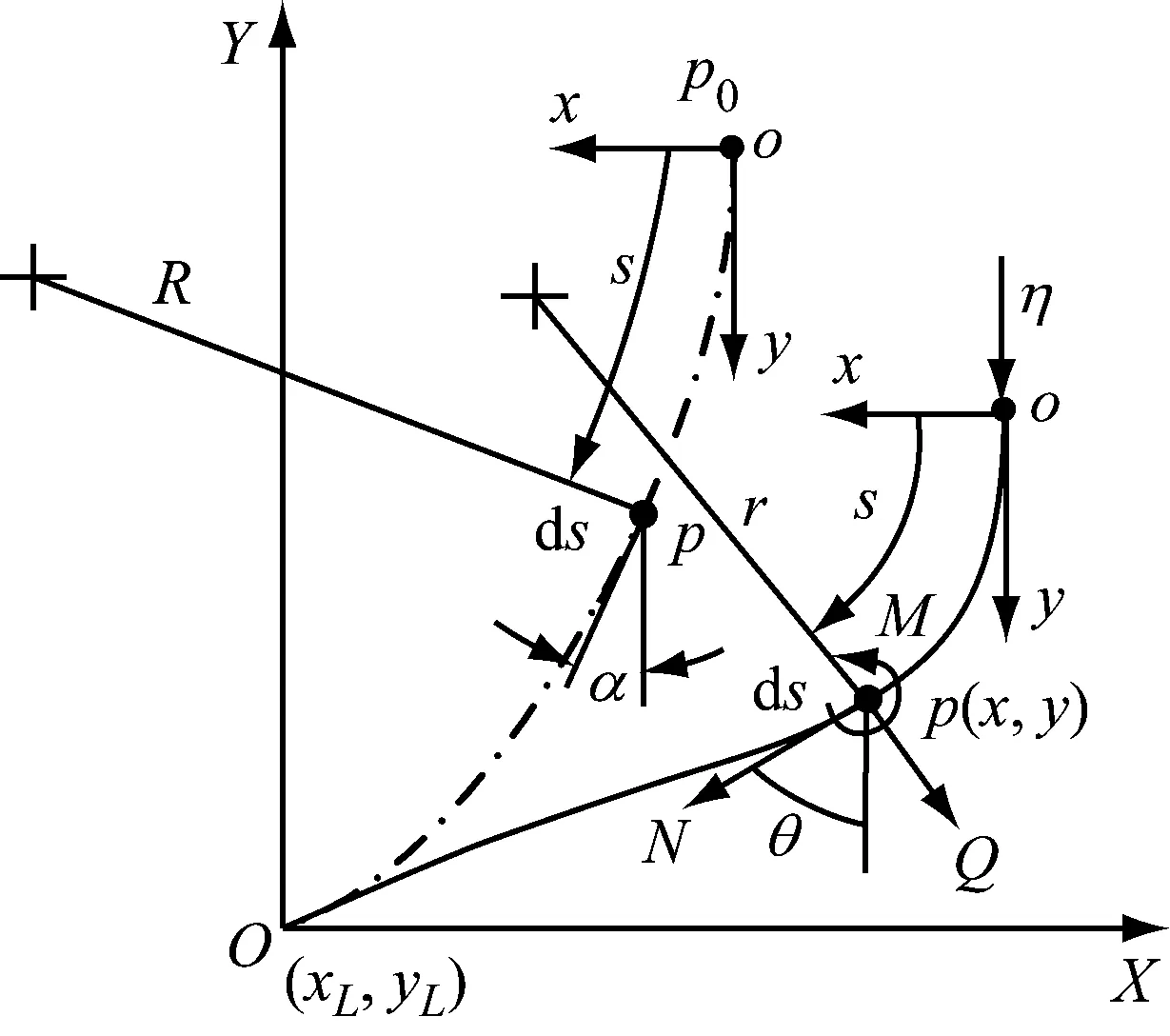
图2 一般曲梁的变形分析

则p处曲梁单元的长度可表示为

ds=r(θ)dθ=Rdα

(1)

式中，R,r分别为点p处变形前后的曲率半径。

根据图2可知曲梁单元的截面轴力N、剪力Q及弯矩M分别为

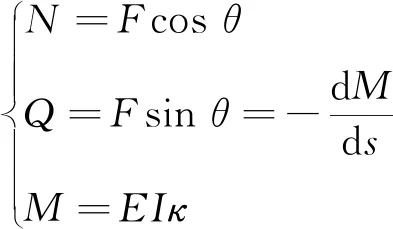
(2)

式中：EI为曲梁的抗弯刚度；κ为曲梁变形后的曲率。

根据Euler-Bernoulli梁理论，有曲梁变形后的几何关系

(3)

浮动坐标系xoy中的点(x,y)在固定坐标系XOY中表示为

X=x-xL，Y=y-yL

(4)

式中，(xL,yL)为曲梁固定端在浮动坐标系中的位置。

由式(2)、式(3)可得曲梁平衡方程

(5)

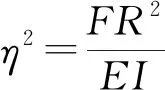
式(5)有通解

(6)

式中：sn和cn为雅可比椭圆正弦和余弦；|k|<1为椭圆函数模；D为积分常数。

一般固支曲梁的边界条件

θ(0)=0，θ(αL)=αL

(7)

2 方程的求解与讨论

2.1 不考虑压板的作用

不考虑压板的作用，压力始终作用于曲梁端部，考虑边界条件θ(0)=0，利用式(6)可得D=0，即

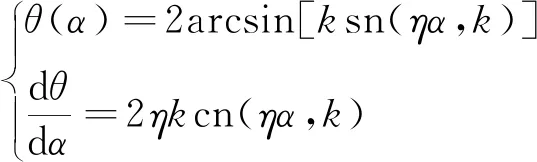
(8)

考虑边界条件θ(αL)=αL，利用式(8)可得

n=0,1

(9)

式中：n为θ在α∈(0,αL)上的极值点数目；K(k)为第二类完全椭圆积分；F(φ,k)为第一类非完全椭圆积分。

当θ恰好有极值点时，即θ在曲梁末端取得极值，有

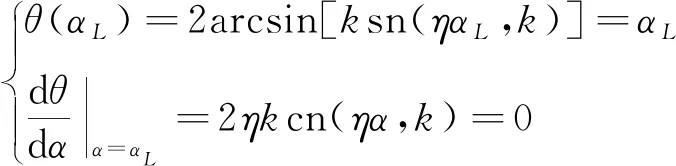
(10)

联立式 (10)可得

(11)

代入式(9)可得θ恰好有极值点时对应的临界外力ηc1

(12)

当η>ηc1时，变形后截面角θ在α∈(0,αL)上有极值，令极值点处变形前的截面角为αc，代入式(8)可得

(13)

极值点对应的未变形的截面角αc可由式(14)求得

(14)

对于给定的压力η，利用式(9)可得到对应的k值,进而由式(8)得到任意点变形后的截面角θ。

进一步由式(8)可得

(15)

式中，dn为雅可比椭圆δ函数。

将式(15)代入式(3)可得梁上任意点的位置

(16)

式中：am为雅克比椭圆幅值函数；E(φ,k)为第二类非完全椭圆积分。

由式(8)可得

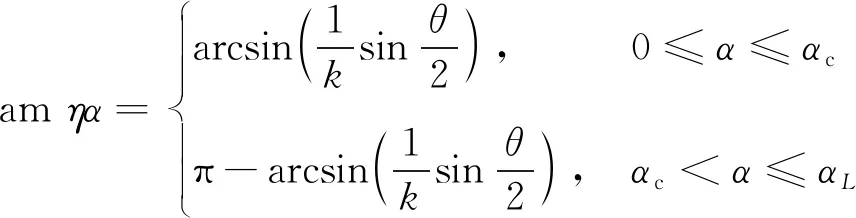
(17)

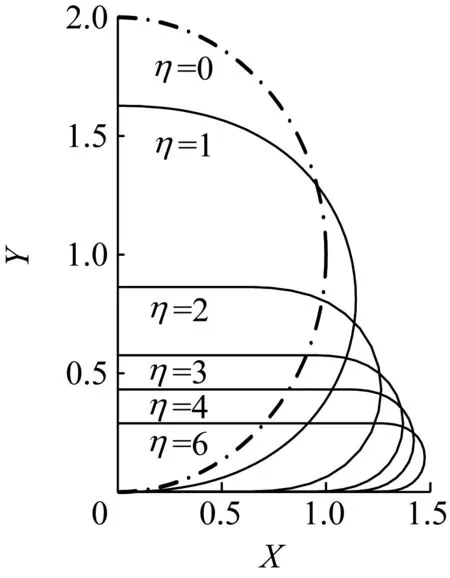
(a) 变形后曲梁位形

2.2 压板间曲梁的大变形分析

考虑压板的作用，始终有Y≥0，当压力η较小时，曲梁与压板仅有一个接触点(端点)，压力作用在曲梁的末端，其变形方式和2.1节的一般情况相同。

随着压力η的增大，曲梁变形随之增加；当η=ηc2时，曲梁中部与压板刚好接触于A点, 如图4所示。

(a)

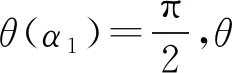
(18)

此时两个接触点A和O等高(即：yA=yL)，有

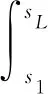
(19)

联立式(18)、式(19)，则可求得：ηc2，k和α1。

随着压力η的进一步增大，当η>ηc2时，η1>0，可对曲梁进行分段研究。

对于oA段曲梁

有边界条件

(20)

由式(6)可得oA段曲梁变形后的截面角及截面角的变化率

(21)

考虑边界条件式(20)，利用式(21)可得

(22)

对于AO段

有边界条件

(23)

由式(6)可得AO段曲梁变形后的截面角及其变化率

(24)

式中，η2=η1-η。

考虑边界条件式(23)，θ在(α1,αL)上有极值。利用式(24)可得

(25)

再由yA=yL，可得

{2E[am(η2α+D2),k2]-F[am(η2α+D2),

(26)

对于给定的压力，利用式(22)、式(25)、式(26)可解得k2，η2，k1，α1和D2，进而由式(21)、式(24)解得曲梁上任意点变形后的截面角θ。

令极值点处的未变形截面角为αc，有

(27)

利用式(27)可得截面角αc

(28)

由式(24)可得

am(η2α+D2,k2)=

(29)

进一步的可得梁上任意点的位置

(30)

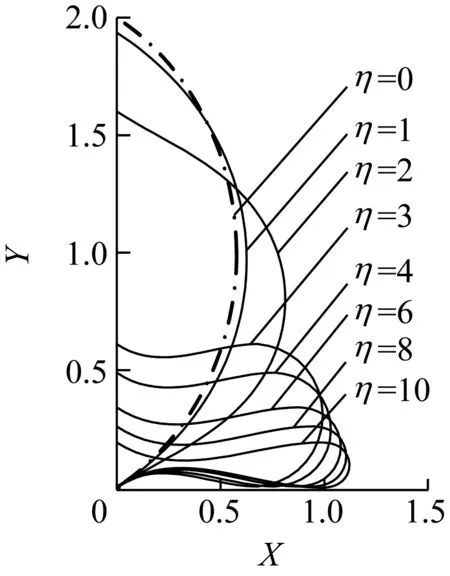
(a) 变形后曲梁位形

当ηc1≤η<ηc2时，压板对曲梁压力的作用点仍然位于曲梁端部，变形后曲梁的截面角θ有极值，θ随着α的增大先增大而后减小至αL；对于相对较大的作用力η，变形后截面角θ的极值也越大，取得极值的α越小。

随着压力η的进一步增大，当η>ηc2时，压板对曲梁压力的作用点离开曲梁端部向中部移动，此时压板与曲梁有两个接触点，变形后曲梁的截面角θ有极值；对于相对较大的作用力η，变形后截面角θ的极值也越小，取得极值的α越小。

(a) 变形后曲梁位形

2.3 曲梁结构的变形及缓冲系数

曲梁缓冲器在受到外界冲击时，如果不考虑机械能的损失，全部冲击能量都转化为曲梁的变形能。因此冲击过程中曲梁结构能够吸收的能量可由其弯曲变形能来描述，对于所研究的半段曲梁的弯曲变形能U可表示为

(31)

利用式(3)，不同压力η作用下所讨论的半段曲梁的弯曲变形能可分别写为

当η≤ηc2时

(32)

当η>ηc2时

η2E[am(η2αL+D2),k2]-

η2E[am(η2α1+D2),k2]}

(33)

冲击过程中作用在曲梁缓冲器上的冲击压力Ftol及在此冲击力下曲梁缓冲器的变形量v(上压板位移)及变形能Utol可分别表示为

(34)

式中：m为组成曲梁缓冲器的曲梁数目；F为作用于单根曲梁上的冲击力。

对于高度为H的曲梁缓冲器，借鉴对实体材料的能量吸收评价方法[24]，曲梁缓冲器的缓冲系数可表示为

(35)

由式(35)可见缓冲器的缓冲系数与曲梁数量m无关，仅取决于曲梁的初始高度H和曲率半径R(或初始安装角αL)以及作用在单根曲梁上的外力η。

具有不同初始安装角αL的固支曲梁缓冲器的力-变形曲线及缓冲系数曲线，如图7所示。可见曲梁缓冲器受压时体现出类似于实体缓冲材料的明显的非线性变形特性，力-变形曲线虽然没有严格的恒力变形阶段，但也具有较为明显的平台阶段；对于相同的压力η，曲梁末端初始安装角αL越小，缓冲器的变形也越小；随着冲击压力η的增大缓冲系数C先是逐渐减小随后开始逐渐增大，有明显的极小值Cmin出现。工程上通常利用缓冲系数的极小值Cmin及其对应的冲击力η作为缓冲设计的参考依据。对于末端初始安装角αL较小的曲梁，缓冲系数的极小值Cmin也较小，意味着缓冲器的总体缓冲性能越好；但由于C取得极小值时对应的压力η较大，表明缓冲器需在较大压力下才具有较好的缓冲性能，意味着其更适用于重型产品的缓冲设计。