常磁场下铁磁矩形薄板的非线性固有振动

2023-02-22陶善泽胡宇达

振动与冲击 2023年3期

陶善泽, 胡宇达

(1. 燕山大学建筑工程与力学学院，河北秦皇岛 066004;2. 燕山大学河北省重型装备与大型结构力学可靠性重点实验室，河北秦皇岛 066004)

随着材料科学的发展进步以及现代科技领域的需要，电磁材料在工业领域和日常生活中得到了长足的发展和广泛的应用。薄板作为工程中常见的一类薄壁结构，其在航空航天、磁悬浮运输、医疗器械等一些特定领域中应用时，有时会处于磁场环境下，并产生复杂的磁固耦合动力学行为。因此对结构在磁场作用下力学特性的研究具有重要理论与实际意义。

目前，国内外学者对板结构的非线性振动问题已进行了许多研究。Twinkle等[1-2]研究了各向同性矩形板和正交各向异性矩形薄板的自由振动问题，分析了频率及振型变化规律。Chen等[3]研究了面内双向功能梯度矩形板在横向简谐激励下的非线性振动问题。Javani等[4]研究了石墨烯薄片增强纳米复合材料圆板的非线性自由振动问题。Sasadhar[5]研究了在周期性激励力作用下含孔非均匀圆薄板的强迫振动问题。胡宇达等[6]针对热环境下的旋转功能梯度圆板，建立了相关力学模型并分析了不同参数对其强非线性固有振动特性的影响。陈万吉等[7]对Mindlin层合板的自由振动问题进行了研究。对于电磁材料结构在磁场中的磁弹性振动及屈曲问题，学者们也取得了许多研究成果。Elham等[8]研究了载流铁磁梁板在磁场作用下的非线性振动行为。Golubeva等[9]研究了铁磁矩形板在纵向磁场中的振动问题。李哲等[10]研究了夹支和简支边界条件下变速运动圆板在磁场中的参强联合共振问题。Yang等[11]基于能量法对在横向、斜向和纵向磁场中的铁磁薄板的磁弹性屈曲问题进行了分析。Kou等[12]对倾斜磁场中铁磁板的谐振特性进行了理论和试验研究。王省哲等[13]针对倾斜磁场环境中铁磁板的非线性弯曲问题进行理论分析。Gao[14]对悬臂矩形软铁磁板在磁弹塑性耦合作用下的屈曲、断裂和弯曲行为进行了分析。胡宇达等[15-16]针对导电圆板在磁场中的共振问题和超谐-组合共振问题进行了研究。Hu等[17]研究了旋转运动圆板的磁弹性轴对称多模态共振和Hopf分岔问题，分析了转速及磁场的影响。Irazu等[18]针对涡流效应对导电梁的振动衰减问题进行了研究，分析了磁场作用下梁结构的振动响应特性。

现有研究表明，对于结构非线性振动以及磁弹性屈曲、导电结构振动等问题的研究相对较多。同时，因软铁磁材料具有较强的磁化效应作用因素，将表现出更加复杂的力学行为，而其中的非线性振动问题也逐渐引起关注，其研究工作还较少。本文针对铁磁材料薄板结构，研究常磁静载作用下系统的非线性振动问题，应用摄动展开法和多尺度法，推得非线性自由振动解析解和固有频率表达式，分析初值、边长比、磁场强度等参量对系统固有振动特性的影响。

1 基本理论

1.1 动能与势能

考虑各向同性铁磁性矩形薄板处于上、下不同区域的外加横向恒定磁场环境中(H1为上部横向磁场强度，H2为下部横向磁场强度)。对于矩形薄板建立直角坐标系(x，y，z)，如图1所示。矩形板厚度为h，长为l，宽为b，质量密度为ρ。以下将通过推导，得出磁场环境下铁磁矩形薄板的磁弹性耦合振动方程。

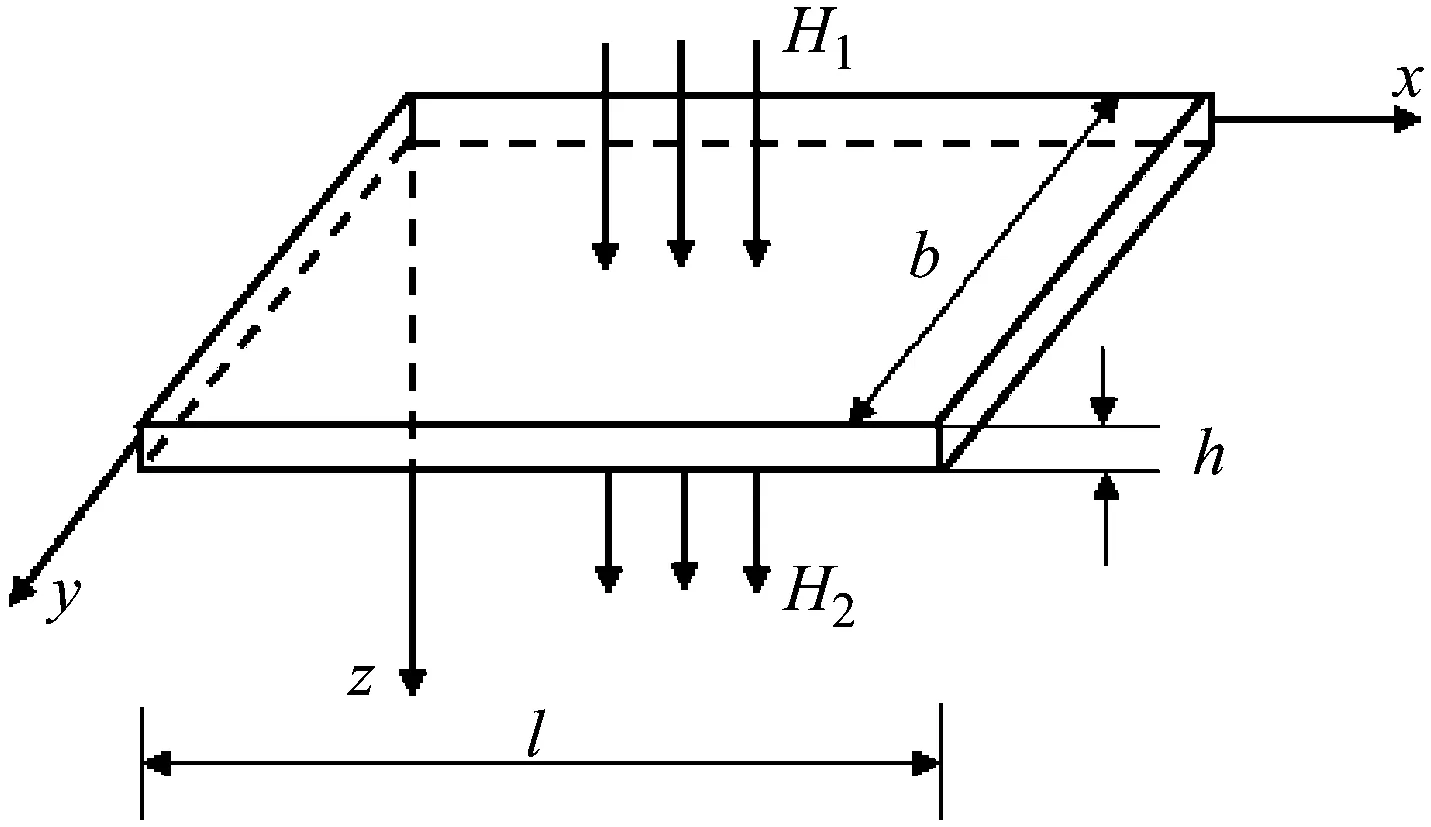
图1 磁场中铁磁矩形板模型

处于外加磁场环境下的铁磁矩形薄板，设板内任取一点的变形位移分量在直角坐标系下可表示为

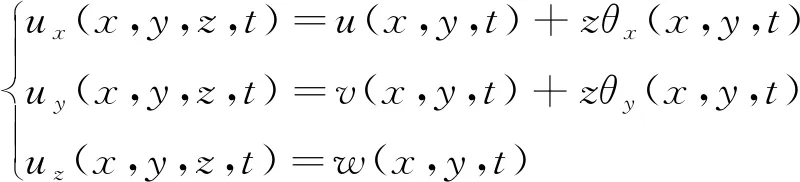
(1)

则矩形板的速度分量可以表示为

(2)

由此可得系统的动能表达式为

(3)

基于弹性理论，板的弯曲形变势能和中面应变势能的表达式分别为

(4)

(5)

1.2 电磁力

根据磁弹性相互作用的理论模型[19]，可得出各向同性软铁磁介质受到的磁化磁体力

(6)

式中：Hni(i=1,2)为矩形板上、下表面处的法向磁场强度，易由电磁边界条件确定；μ0为真空磁导率；μr为相对磁导率；χm为材料的磁化率，χm=μr-1。

磁场中铁磁矩形板所受洛伦兹力表达式为

f(fx,fy,fz)=J×B

(7)

式中：J=σ0(V×B)为电流密度矢量；B=μ0μrH为磁感应强度矢量；σ0为电导率。

设在矩形板内部，磁场沿轴z线性分布，则

(8)

根据式(2)和式(7)，并忽略面内位移，可得直角坐标系下铁磁矩形板所受各方向洛伦兹体力为

(9)

将式(9)沿板厚方向z进行积分，可进一步求得薄板所受的单位面积电磁力矩式

(10)

(11)

故横向磁场中铁磁矩形板所受总电磁力的虚功式为

(12)

1.3 振动方程

根据哈密顿变分原理，有

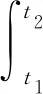
(13)

式中，t1和t2为积分时间域。最后将式(3)～式(5)代入到式(13)，整理得铁磁矩形薄板的横向磁弹性振动方程为

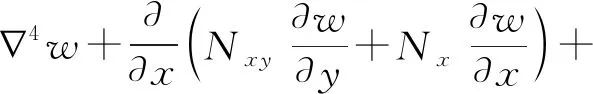
(14)

其中，几何非线性下的中面内力表示为

(15)

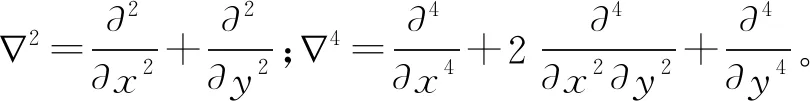
2 静磁力作用下矩形板振动方程

对于横向常磁场环境下的铁磁矩形板，将式(6)、式(10)、式(11)和式(15)代入式(14)中，可得到如下含常磁静载项的位移型非线性振动方程

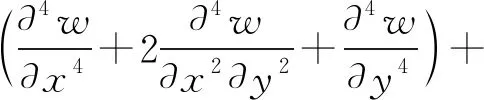
(16)

设矩形板在静磁力Q作用下产生的静挠度w0，振动时的扰动挠度为w1，则总挠度可摄动展开为

w=w0+w1

(17)

初始挠度w0满足方程：

(18)

对于四边简支边界条件，设

(19)

将式(19)代入式(18)，可求得如下确定f0的代数方程

(20)

其中

同样，再将扰动位移函数设为

(21)

最终，将式(17)代入式(16)，并结合式(21)和式(19)及求得的f0，通过伽辽金离散可推得扰动振动方程为

A1q″(t)+A2q′(t)+A3q(t)+A4q2(t)+

A5q3(t)=0

(22)

其中

3 非线性振动解析解和固有频率

下面对呈现弱非线性特征振动系统的非线性固有振动问题进行解析求解，并将式(21)写为

ε2B3q3(t)=0

(23)

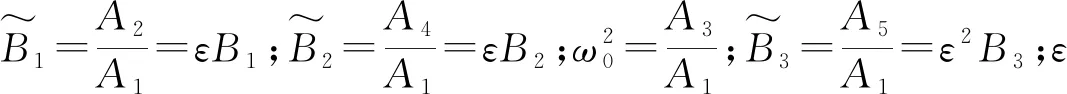
用多尺度法求解微分方程，在时间尺度上讨论二次近似解，取T0=t，T1=εt，T2=ε2t。则振动微分方程的近似解可表示为：

q(t,ε)=q0(T0,T1,T2)+εq1(T0,T1,T2)+

ε2q2(T0,T1,T2)

(24)

将式(24)代入式(23)，令ε的同次幂项相等得到

(25)

(26)

(27)

式(25)的通解为

(28)

将式(28)代入式(26)得

(29)

式中，cc为左边各项的共轭复数。为消除避免久期项，可得

(30)

从而解得

(31)

将式(28)和式(31)代入式(27)右边，为消除久期项，可得

(32)

从而解得

(33)

为确定复数函数A，将A对t的导数写作

(34)

再将复函数A写作指数形式

(35)

将式(35)代入式(34)并应用式(29)和式(32)，进行实部与虚部分离得

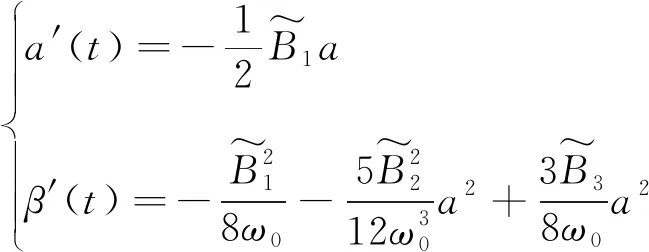
(36)

其解为

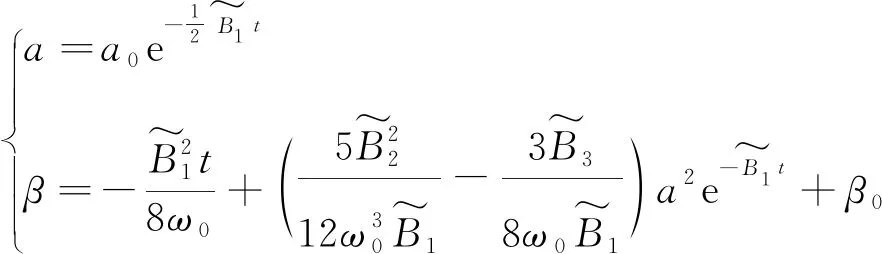
(37)

式中，a0和β0均为取决于初始条件的积分常数。

最终，将以上求得的各幂次解代回式(24)，得出非线性振动系统的二次近似解为

(38)

其中

(39)

从而得到系统的首阶非线性固有振动频率为

(40)

4 算例分析

对于横向磁场中受静磁力作用的铁磁矩形薄板，在四边简支边界条件下进行算例分析，矩形薄板长l=0.6 m，宽b=0.2 m，所选材料物理参数如表1所示。

表1 薄板物理参数

4.1 结果对比

3种不同材料矩形板，其数值解与解析解的响应图与相图结果对比图，分别如图2、图3所示。其中，数值解采用龙格库塔法对微分方程式(22)进行求解，解析解为采用多尺度法求得的结果式(38)而计算得到的，并将获得的数值解与解析解的响应图和相图进行对比分析。由图2及图3可见，数值解与解析解的曲线基本吻合，验证了本文采用多尺度法求解的正确性。

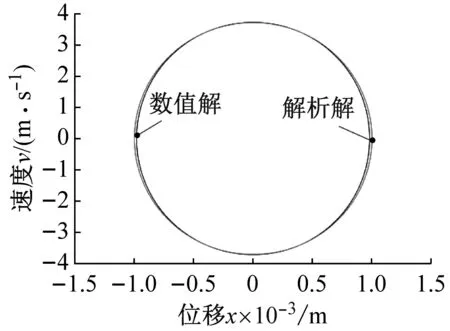
(a) 低碳钢

4.2 固有频率随时间变化规律

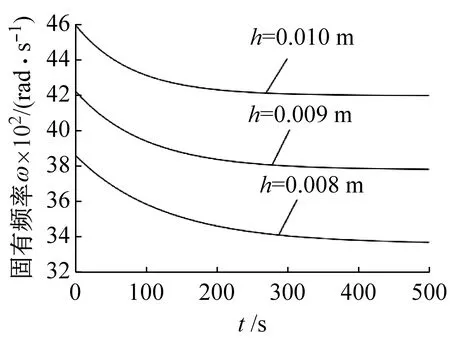
3种不同材料的矩形薄板，在取板厚、初值和磁场强度不同时，固有频率随时间变化的特性规律曲线图,分别如图4～图6所示。由3幅图均可看到，随着时间的增加，3种材料铁磁矩形板的固有频率会趋于定值。其原因在于，本文采用多尺度法求得的非线性固有振动频率式(40)中，存在一个含时间t的负指数衰减项，故当时间增大时，固有频率值将逐渐变小，最终会趋于一定常值，只在初始阶段固有频率随时间有明显变化，体现了系统的非线性振动特性。

图4中曲线表明，当磁场存在时，板厚越大，频率越大，且随着时间的增加而逐渐减小。由图5可知，当初值不同时，频率的初始值也不同，并且当初值越大时，频率初始值也越大；但是随着时间的增加，初值的影响越来越小，频率值快速下降，最终趋于一定值。图6中曲线表明，当上、下表面磁场强度均为零时，固有频率不随时间的增加而发生变化，此时相当于无外加磁场情况；当上表面磁场强度为零，而下表面磁场强度不为零时，其固有频率随时间的增加而逐渐减小。对比图6(a)～图6(c)中各材料的频率变化曲线可知，当上下表面磁场强度均为零，即无磁场情况时，马氏体钢和低碳钢材料矩形板的固有频率大小相当，而灰铸铁材料的固有频率明显偏小；根据表1可知，这是由材料物理参数的不同导致的。

(a) 低碳钢

通过龙格库塔法求解得到的不同初值时，3种不同材料矩形薄板的功率谱图，如图7所示。将各图中不同材料矩形板的固有频率与图5进行比较，结果基本一致，说明了本文解析解的可靠性。

(a) 低碳钢

4.3 频率随不同特征参数变化规律

3种不同材料的矩形薄板，当板厚不同时，其固有频率随初值变化的特性规律曲线图，如图8所示。由图8可知，3种材料的固有频率随初值的变化规律有相同之处：板厚越大，固有频率越大；随初值的增大，其振动频率也随之增大。通过对比图8(a)～图8(c)，即3种材料的频率变化关系曲线可知，其不同之处为：低碳钢材料矩形板的固有频率随初值增大而增大最多，其次是灰铸铁，最后是马氏体钢；且对于低碳钢和灰铸铁材料，板厚增大会使固有频率的增大幅度变小。出现上述的原因可根据固有频率表达式得到，当选定一种材料且时间及其他参数确定时，固有频率的大小主要由初值所在的衰减项决定，且衰减项为正，故初值越大固有频率越大；当其他参数和时间均相同时，可知固有频率的增大幅度主要受衰减项中指数项影响，对比3种材料的物理参数并考虑式(40)，故可得出各材料频率受初值影响大小的顺序依次为：低碳钢、灰铸铁、马氏体钢。

(a) 低碳钢

3种不同材料的矩形薄板，当取不同初值时，其固有频率随边长比g(矩形板短边长度与长边长度的比值)变化的特性规律曲线图，如图9所示。由图9可知，对于3种材料均有：在给定相同参数时，随矩形板边长比的增大，其固有频率随之减小。对于马氏体钢材料的矩形薄板，观察图9(c)中频率随边长比的变化关系曲线，分析频率表达式(40)中各参数之间的关系可知，当边长比增大到一定值时，与初值项相关的衰减项中会出现为零的情况，故不同初值的频率曲线会相交于一点，在交点的左侧，初值越大，固有频率越大；在交点的右侧，初值越大，固有频率反而越小；由低碳钢和灰铸铁材料的频率变化关系曲线可知，在边长比一定时，初值越大，其固有频率越大。

(a) 低碳钢

3种不同材料的矩形薄板，当取不同板厚时，其固有频率随边长比g变化的特性规律曲线图，如图10所示。由图10可知，对于3种材料均有：固有频率随边长比的增大而减小。对于马氏体钢材料，基于得出的固有频率表达式(40)可知，当边长比取特定值时，存在相同的固有频率值，此时3条曲线交于一点，并使得左、右侧的频率呈现不同变化规律。对于低碳钢和灰铸铁材料，由图10(a)和图10(b)可知，在边长比一定时，板厚越大，其固有频率越大。

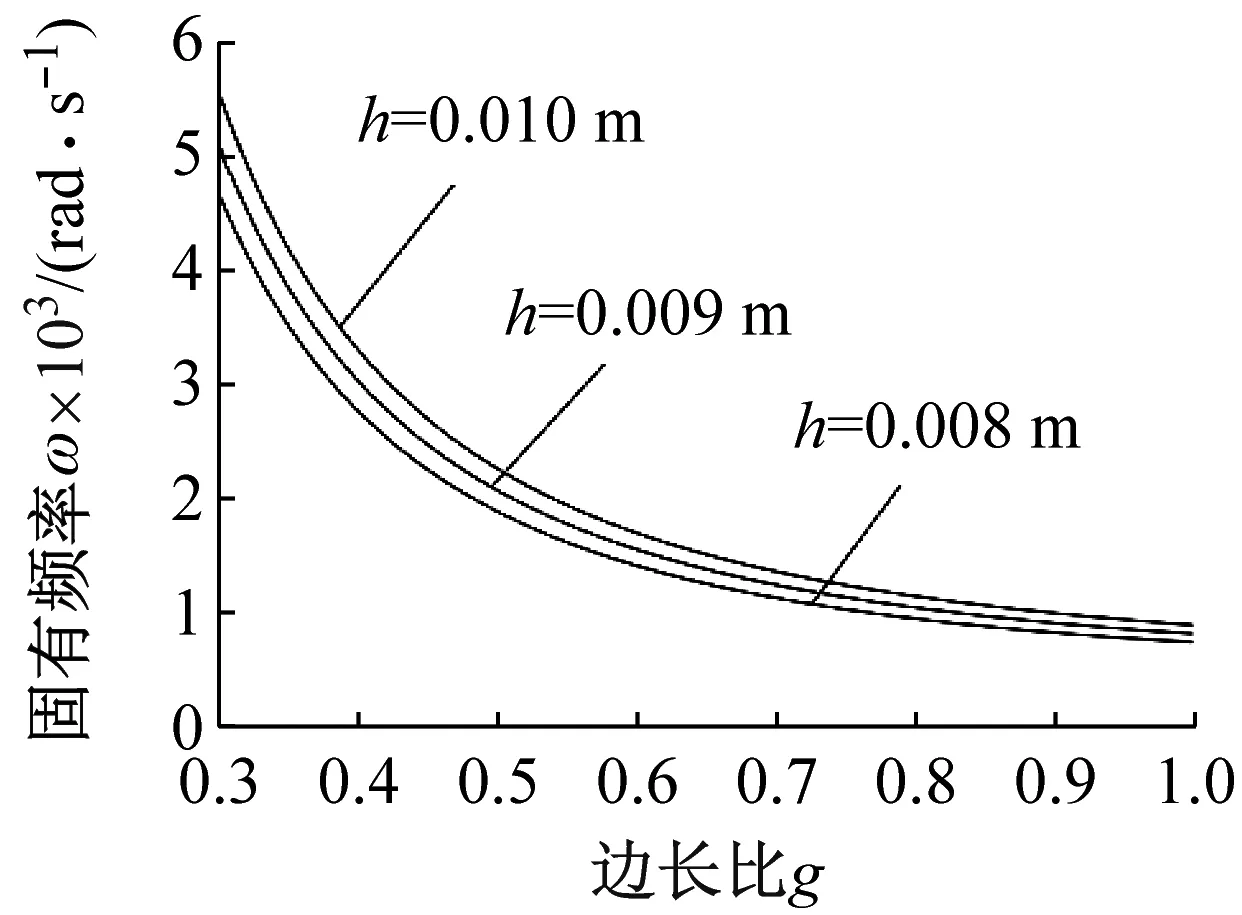
(a) 低碳钢

3种不同材料的矩形薄板，当其处于上、下表面磁场强度之和一定的磁场环境中，取不同初值和不同板厚时，其固有频率随下表面磁场强度变化的特性规律曲线图，如图11、图12所示。从两图中均可看出，低碳钢和灰铸铁材料在上述磁场条件下，其频率随下表面磁场强度的增大，并无明显变化。而材料为马氏体钢的矩形板固有频率随下表面磁场强度的增大有明显变化趋。

由图11知，当初值取值很小时，系统频率随磁场强度的增大先减小到最低点再增大，当初值取值超过一定数值时，系统频率会随磁场强度的增大而呈现相反趋势，先增大到最高点，然后再减小。出现这种情况的原因由固有频率表达式(40)可知，当其他参数确定并取上述磁场条件时，对于低碳钢和灰铸铁材料，随下表面磁场强度的增大其频率表达式中衰减项所受影响很小，故频率无明显变化；而对于马氏体钢材料，其衰减项所受影响较大，故曲线有明显变化；当上下表面磁场强度相等时，出现极值点，此时衰减项最大，频率达到峰值。

(a) 低碳钢

由图12可知，对3种材料均有：板厚越大，固有频率越大。对于马氏体钢材料矩形板，其固有频率随下表面磁场强度的增大呈现出先减小后增大的趋势。出现这种现象是因为，当其他条件确定，且取上述磁场条件时，对于低碳钢和灰铸铁材料，下表面磁场强度的增大对频率衰减项的影响很小，故曲线无明显变化；而对于马氏体钢材料，可知其频率表达式中衰减项受磁场强度的影响并不是很小，故可看出其变化。