钢纤维地质聚合物混凝土冲击力学性能研究
2023-02-22叶建峰刘宪成颜桂云黄冠骅庄金平
叶建峰, 刘宪成, 颜桂云, 黄冠骅, 庄金平
(福建工程学院 福建省土木工程新技术与信息化重点实验室, 福州 350118)
地质聚合物混凝土通过工业废弃物粉煤灰、矿渣为主要原料替代普通硅酸盐水泥,实现了废弃资源再利用,且地质聚合物混凝土具有早强快凝、结构较密、渗透率低、耐高温、隔热效果好等良好的性能[1-4],是环境友好型的绿色建筑材料,引起了许多国内外研究者的兴趣,成为国内外研究非常活跃的材料之一。
开展钢纤维地质聚合物混凝土抗冲击力学性能的研究对于结构安全具有重大意义。目前,各学者对于其动态力学行为进行了一定的探索。鲁强等[5]研究指出同普通混凝土类似,地质聚合物混凝土的峰值应力、峰值应变及抗压强度均有显著的应变率强化效应;杨健辉等[6]研究指出在混凝土中掺入纤维可改善结构力学性能,具有明显的强度及能量效应;王志坤等[7]研究发现应变率的对数同地质聚合物混凝土的DIF(dynamic increasing factor)呈明显的线性关系,而高温对于地质聚合物混凝土动态抗压强度有不利作用;陶鑫等[8]研究指出钢纤维掺量的提高会增强地质聚合物混凝土的强度、弹性模量及延性等力学性能;罗立峰[9]研究揭示了钢纤维聚合物改性混凝土具有良好的抗冲击性能可作为桥面铺装的理想复合材料;潘慧敏等[10]揭示了钢纤维对混凝土基体脆性的改善效应,其韧性系数最大提升近基准混凝土的10倍。已有研究表明,地质聚合物混凝土相较于普通硅酸盐混凝土而言,其脆性更为明显,加入钢纤维为解决其脆性等缺陷提供了可行的方法,但研究仍不充分,且缺少关于钢纤维地质聚合物混凝凝土的抗冲击应力-应变本构模型的研究。因此,有必要对钢纤维地质聚合物混凝土的抗冲击力学性能做进一步的研究。
本文通过控制粉煤灰、矿渣的用量配制不同基准强度的地质聚合物混凝土,再掺入不同体积量的钢纤维制备出钢纤维地质聚合物混凝土试件。采用直径为80 mm的霍普金森压杆(split Hopkinson pressure bar,SHPB)对在不同冲击气压(对应不同应变率)、不同体积钢纤维掺量的地质聚合物混凝土的抗冲击性能进行研究,探究钢纤维对试件的破坏形态、应力应变曲线、韧性指数等力学性能的影响,并建立钢纤维地质聚合物混凝土的动态应力-应变本构模型。
1 试验设计
1.1 试件制备
原材料:细骨料(细度模数为2.65,表观密度及堆积密度分别为2.65 g/cm3,1.55 g/cm3,含有少量杂质的中粗砂);粗骨料(粒径9~12 mm,表观密度及堆积密度分别为2. 72 g/cm3,1.68 g/cm3,吸水率0.65%,压碎指标为8.3%的天然碎石);高炉矿渣(密度2.92 g/cm3,比表面积460 m2/kg,28 d活性指数大于95%,含水量小于1.0%的高炉矿渣粉);粉煤灰(密度2.34 g/cm3,比表面积800 m2/kg,28 d活性指数大于65%,含水量小于5.0%的Ⅱ级F类粉煤灰);钢纤维(镀铜微丝型钢纤维,密度7.8 g/cm3,直径0.2 mm,长度13 mm,如图1所示);碱激发剂(采用纯度为99%的片状固体氢氧化钠(NaOH),模数为3.4,波美度为39°Bé,氧化钠、二氧化硅及水含量分别为7.4%,27.6%,65%的硅酸钠水玻璃,采用自来水作为拌合水)。
图1 镀铜微丝型钢纤维
试验共设置了15组普通地质聚合物混凝土配合比,钢纤维的掺入根据JGJ/T 221—2010《纤维混凝土应用技术规程》进行,其他材料的用量根据JGJ 55—2011《普通混凝土配合比设计规程》进行。经过合理配置获得所需基准强度配比后,将溶胶比控制在0.55,在此基础上,通过控制粉煤灰、矿渣用量和外掺体积率分别为0.3%,0.6%,0.9%,1.2%的钢纤维来配制不同强度的钢纤维地质聚合物混凝土。各组地质聚合物混凝土试件试验配合比,如表1所示。
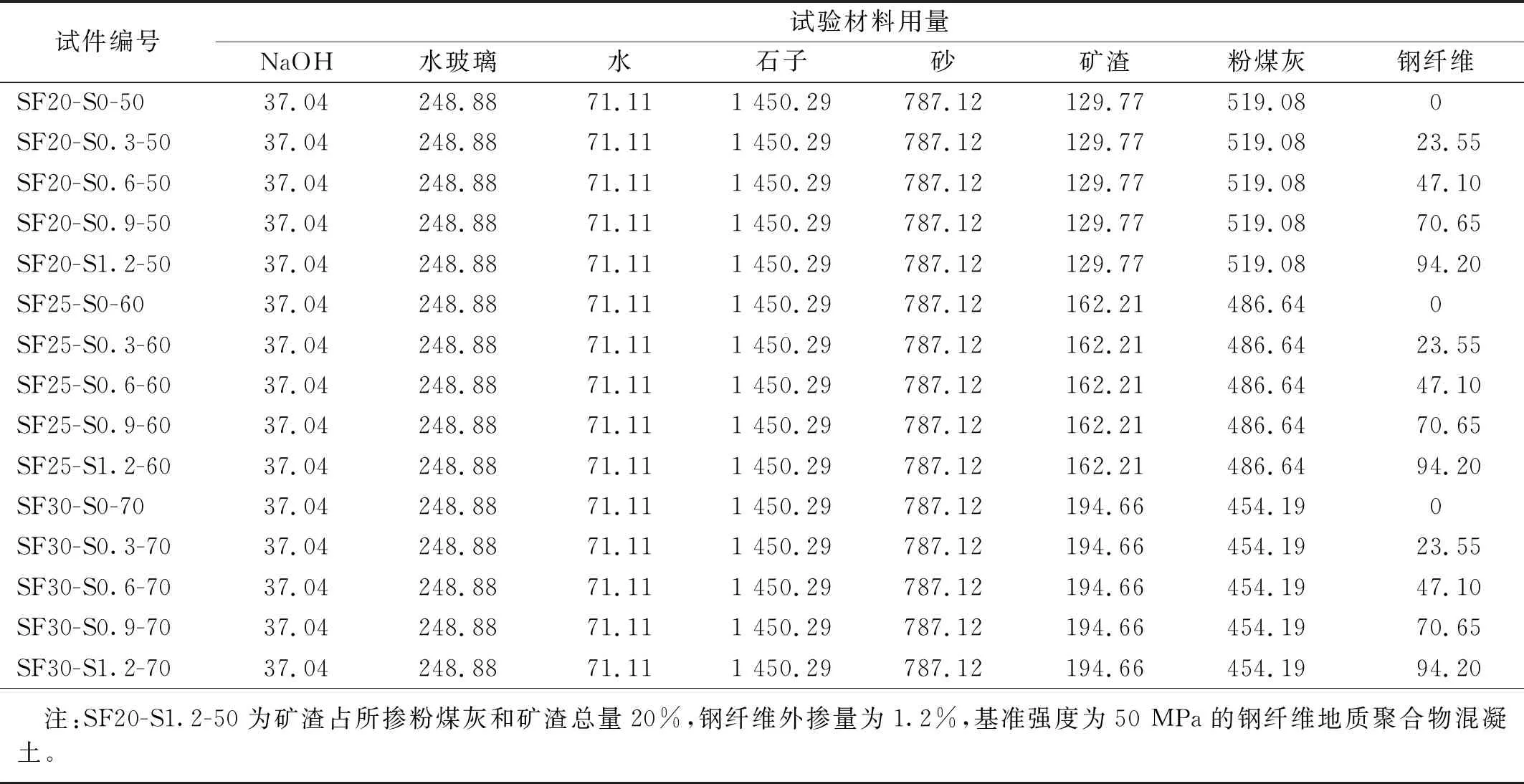
表1 各组地质聚合物混凝土试验配合比
试件制作尺寸为Φ72 mm×36 mm的圆柱体冲击试件15组,每组在3种不同冲击气压作用下重复试件3个,共计试件135个。经搅拌完成后,将事先准备好的PVC(polyvinyl chloride)管进行混凝土浇筑,并置于室外进行自然养护28 d。经加工脱模后的SHPB试件,如图2所示。

图2 SHPB试件
1.2 试验装置
分离式SHPB装置主要由试验加载装置、压杆系统、数据采集及处理系统三部分组成。
(1) 加载装置。主要由高压气瓶及气压控制系统两部分组成。通过气压调节系统可控制纯氮输入量来获得所需的冲击压缩气压值,进而可赋予撞击杆不同的冲击速度。
(2) 压杆系统。由撞击杆、入射杆、透射杆和吸收杆等部分组成,4种杆件等截面(即有相同的直径)所用的材质相同,如图3所示。试验过程中入射杆杆端需贴尺寸为Φ20 mm×1 mm的黄铜片减小横向惯性效应和波形弥散效应[11-13]。

(a) 试件放置
(3) 数据采集及处理系统。主要包括测速系统、电阻应变片、超动态应变仪等。
1.3 试验加载
为了试件的抗冲击性能,分别采用70 s-1,110 s-1,210 s-1作为试件的理论应变率,由文献[14]方法,确定不同理论应变率对应的冲击波速分别为15.3 m/s,19.9 m/s和22.9 m/s。通过测试该SHPB冲击速度与冲击气压的对应关系,最终获得当气压为0.35 MPa,0.45 MPa,0.55MPa时,满足理论应变率要求。因此,确定加载气压分别为0.35 MPa,0.45 MPa,0.55 MPa。
2 试验结果及分析
2.1 钢纤维地质聚合物混凝土试件应力-应变曲线
试件的动态抗压强度与应力-应变曲线由采集到的脉冲信号经分析后得到。各试件典型应力-应变曲线如图4所示,以SF20-S0-50-70 s-1-1标注为例:“SF20”为矿渣量占掺粉煤灰与矿渣总量的20%;S0为钢纤维体积掺量为0;“50”为基准强度为C50的普通地质聚合物混凝土;“70 s-1”为试件的应变率;“1”为重复试件编号。钢纤维地质聚合物混凝土SHPB力学特征量,如表2所示。
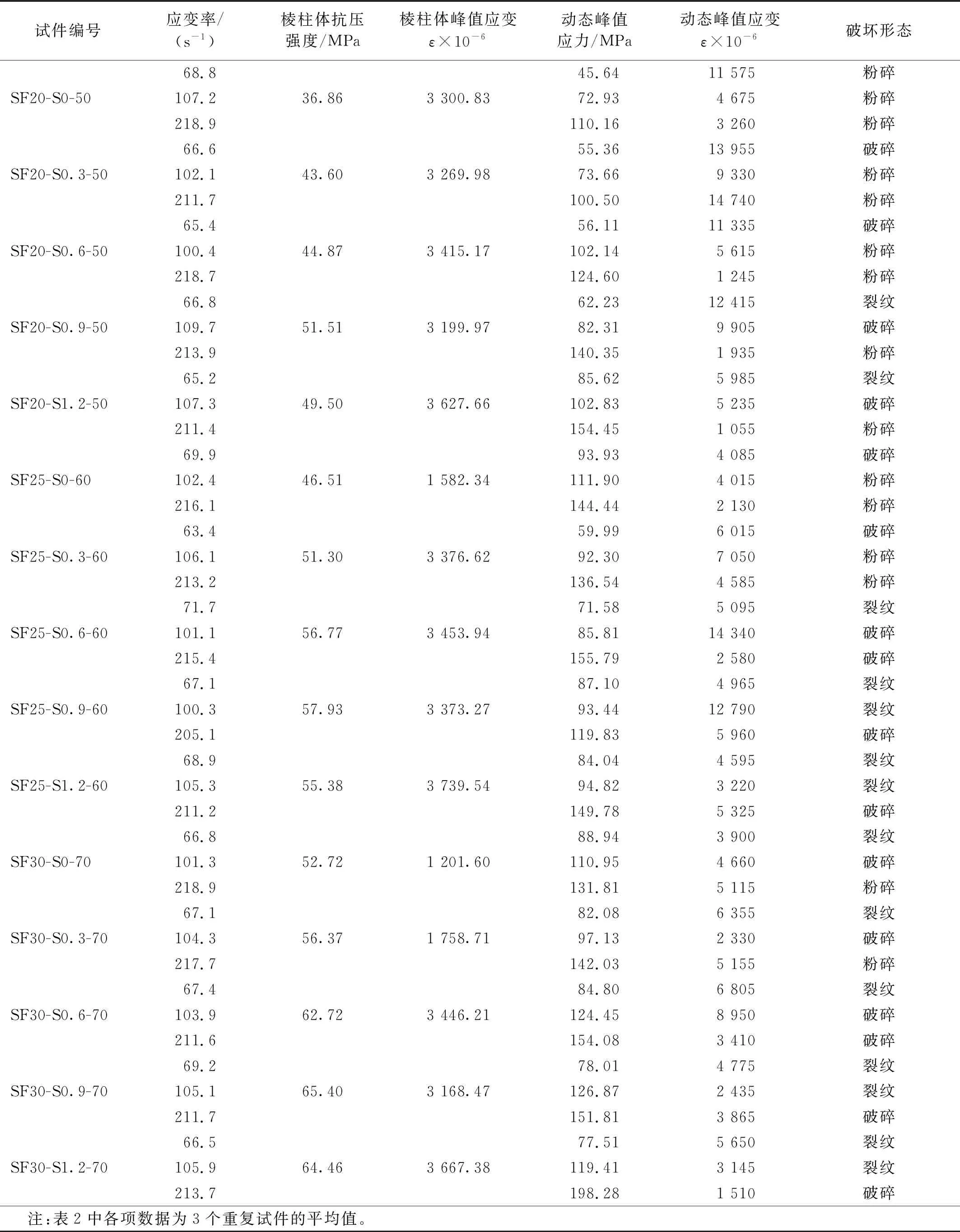
表2 钢纤维地质聚合物混凝土SHPB力学特征量

(a) SF20-S0-50
2.2 应变率对钢纤维地质聚合物混凝土动态抗压性能的影响
试件在不同应变率下动态抗压强度的变化,如图5所示。由图5可知,冲击荷载作用下钢纤维地质聚合物混凝土试件的动态抗压强度均随着应变率的增大呈现逐渐增大的趋势。以SF20-S0.6-50为例,当应变率为65.4 s-1,100.4 s-1,218.7 s-1时,试件对应的动态抗压强度分别为56.11 MPa,102.14 MPa,124.60 MPa。
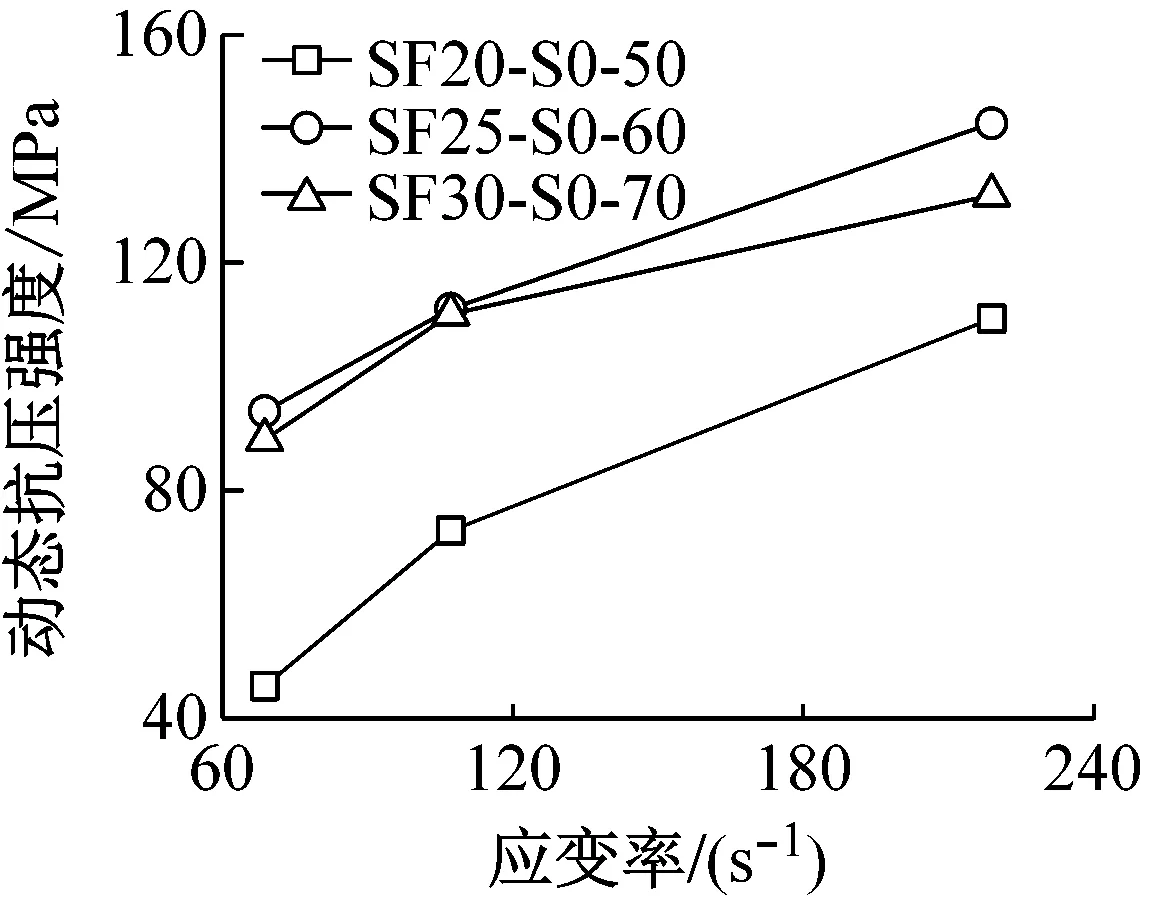
(a) 0钢纤维掺量
钢纤维参量0.6%、混凝土基准强度C50的试件在不同应变率下的破坏形态,如图6所示。由图6可知,随着应变率的提高,钢纤维地质聚合物混凝土试件的完整性逐渐变差,可知试件抗冲击性能的应变率相关性较高,与已有文献中对普通钢纤维混凝土的描述相一致[15]。试件整体由最初的小块碎屑脱落转变为开裂成诸多碎块,这是由于随着应变率的提高,试件通过开展更多的裂纹或破碎成块状来消耗冲击能量。

(a) 70 s-1
2.3 钢纤维掺量对钢纤维地质聚合物混凝土动态抗压强度的影响
钢纤维地质聚合物混凝土试件动态抗压强度与钢纤维掺量之间的关系,如图7所示。对于C50基准强度混凝土而言,其动态抗压强度随着钢纤维掺量的提高有着明显的增大趋势,当应变率为70 s-1时,随着钢纤维掺量的提高,试件动态抗压强度由最初的45.64 MPa增长到85.62 MPa,增幅87.6%;当应变率为210s-1时,随着钢纤维掺量的提高,试件动态抗压强度由最初的110.16 MPa增长到154.45 MPa,增幅40.2%。但对于C60和C70基准强度混凝土,随着钢纤维掺量的增大,其动态抗压强度变化不大。表明,钢纤维掺量对较低强度地质聚合物混凝土的动态抗压强度影响较大,而对强度较高的地质聚合物混凝土影响不大。
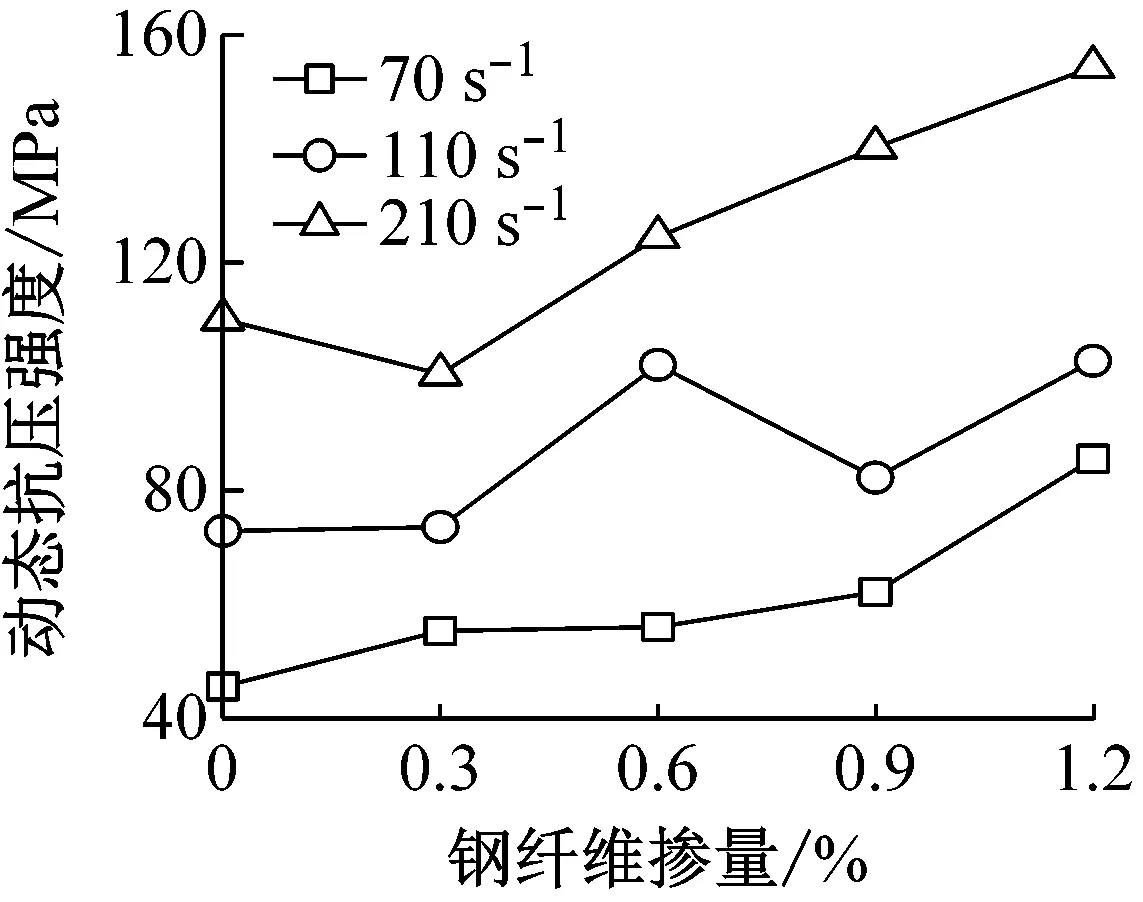
(a) C50基准强度混凝土
不同钢纤维体积掺量的试件在相同冲击气压下的破坏模态,如图8所示。由图8可知,随着钢纤维掺量的提高,试件的完整性逐渐提高。这是由于钢纤维地质聚合物混凝土试件在冲击荷载作用下,钢纤维可在裂缝处起到桥接作用,有效阻止裂缝进一步扩大,并通过自身的变形来消耗冲击能量,同时由于钢纤维与内部混凝土之间黏结力的存在,可使更多的内部混凝土参与到冲击耗能中,避免了试件出现破坏的贯穿裂缝,从而使试件在承受相同动态荷载下的破坏形态向较为完整的方向发展。

(a) S0
2.4 混凝土基准强度对钢纤维地质聚合物混凝土动态抗压强度的影响
试件混凝土基准强度对动态抗压强度的影响,如图9所示。由图9可知,随着混凝土基准强度的提高,钢纤维地质聚合物混凝土的动态抗压强度整体呈增大的趋势。当应变率为70 s-1,钢纤维掺量为0.6%时,3种混凝土基准强度对应的动态抗压强度分别为56.11 MPa,71.58 MPa,84.80 MPa,其动态抗压强度最大提高了51.1%;当应变率为110 s-1时,3种混凝土基准强度对应的动态抗压强度分别为102.14 MPa,85.81 MPa,124.45 MPa,其动态抗压强度最大提高了21.8%;当应变率为210 s-1时,3种混凝土基准强度对应的动态抗压强度分别为124.60 MPa,155.79 MPa,154.08 MPa,其动态抗压强度最大提高了23.7%。

(a) 0钢纤维掺量
在钢纤维掺量0.6%、应变率70 s-1下不同混凝土基准强度试件的破坏形态,如图10所示。由图10可知,随着混凝土基准强度的增加,冲击荷载作用下试件的整体性更好,抗冲击性能更高。主要由于随着矿渣含量的提高(亦即混凝土基准强度的提高),试件内部材料水化反应更为充分,大量的水化产物对结构内部薄弱区进行了填补,起到了很好的黏结作用,试件的完整性逐渐提高且力学性能得到了改善,整体的开裂碎块减少且碎块体积增大。

(a) C50
2.5 钢纤维地质聚合物混凝土的变形性能
采用ASTM C1018能量比值法获取钢纤维地质聚合物混凝土韧性指数,并探究混凝土基准强度、钢纤维掺量及应变率与韧性指数之间的关系。标准的ASTM C1018能量比值法体系示意图,如图11所示。εcr为0.85倍峰值应力对应的应变,用其表示试件初裂时的应变;I1为当应变为3εcr时对应的曲线包裹面积与当应变为εcr时对应曲线包裹面积的比值;I2为当应变为5εcr时对应的曲线包裹面积与当应变为εcr时对应曲线包裹面积的比值;I3为当应变为15.5εcr时对应的曲线包裹面积与当应变为εcr时对应曲线包裹面积的比值,计算公式如式(1)所示。
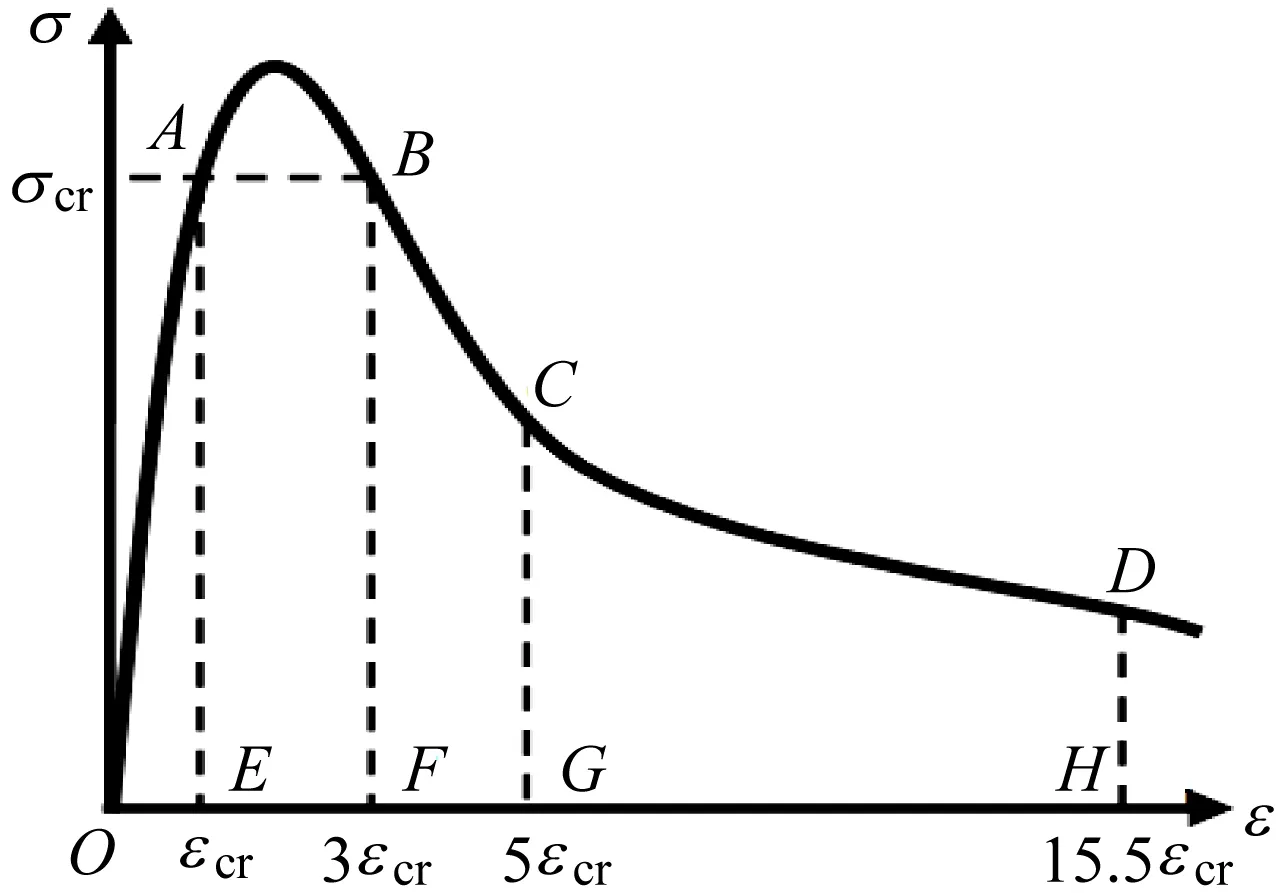
图11 ASTM C1018韧性指数评价法
(1)
采用式I1计算获得各组试件的韧性指数,韧性指数与钢纤维掺量、应变率及混凝土基准强度之间的关系,如图12所示。由图12可知,在相同应变率与混凝土基准强度下,随着钢纤维掺量的增加,试件的韧性指数整体呈现增大的趋势,说明钢纤维改善了试件的韧性性能。主要原因为:当钢纤维掺入地质聚合物混凝土试件后,钢纤维被结构内部的水化产物及砂浆充分包裹,在试件内部矿渣、粉煤灰等胶凝材料与骨料形成的界面过渡区及裂缝处起到了桥接作用,有效地阻止了试件内部裂缝发展,降低了试件内部裂缝数量,对试件的韧性起到了改善作用。

(a) SF20-C50
试件在相同混凝土基准强度与钢纤维掺量时,冲击荷载作用下的韧性指数随着应变率的增大而逐渐增大,以SF20-S0.3-50为例,当应变率为62.6 s-1,102.1 s-1,211.7 s-1时,其韧性指数分别为2.72,3.35,4.35。主要原因是由于试件在冲击荷载作用下,应变率越高,试件内部的裂缝开展来不及发展,试件在冲击荷载作用下表现出的动态抗压强度就越高,从而试件的韧性指数就越高。
在相同应变率下,随着混凝土基准强度的提高,各试件的韧性指数逐渐增大。以钢纤维掺量为0.6%为例,当应变率为70 s-1时,3种基准强度混凝土对应的韧性指数分别为2.94,4.19,4.98,其韧性指数最大提高了69.4%;当应变率为110 s-1时,3种基准强度混凝土对应的动态抗压强度分别为3.13,4.72,5.45,其韧性指数最大提高了74.1%;当应变率为210 s-1时,3种基准强度混凝土对应的韧性指数分别为4.33,5.39,6.17,其韧性指数最大提高了42.5%。同时也表明,试件的韧性指数也具有明显的应变率效应。
3 ABAQUS软件数值分析与验证
采用ABAQUS软件对钢纤维地质聚合物混凝土试件进行了SHPB数值模拟,与试验结果进行对比分析与验证。
3.1 有限元模型的建立
为了实现钢纤维三维的随机分布,采用 Python 编写了随机纤维分布模型代码子程序。采用蒙特卡洛方法,使用Python语言中的random命令,生成区间在(0,1)上的伪随机数,采用Truss单元作为钢纤维,进行部分体积的替代,Python编写的钢纤维随机分布三维图形,如图13所示。
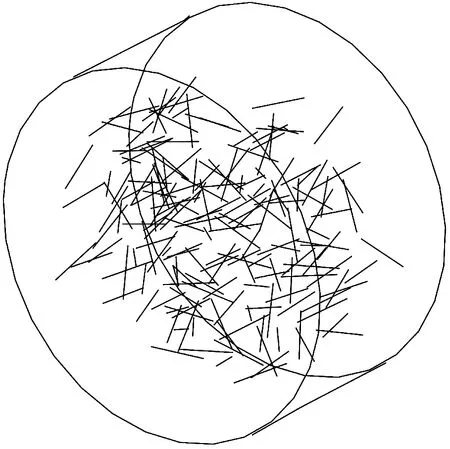
图13 钢纤维随机分布三维图
ABAQUS软件数值模型,如图14所示。图14中从左到右依次为入射杆、钢纤维地质聚合物混凝土试件和透射杆。在SHPB有限元模拟过程中,包含了两个接触条件,即入射杆与试件前表面的接触,透射杆与试件后表面的接触。在整个试验过程中,这两个接触面都均匀的涂满了凡士林,以减小试件与SHPB之间摩擦力的影响。因此,在有限元建模中,将这两对接触均定义为面面接触,法向接触定义为硬接触,切向接触则采用罚函数来定义摩擦,取摩擦因数为0.01。钢纤维地质聚合物混凝土的损伤演变采用混凝土损伤塑性模型。压杆系统在试验中呈弹性,定义压杆材料为各项同性,弹性模量为220 GPa,泊松比为0.20,密度为7 800 kg/m3。采用动力显式分析(Dynamic,Explicit)算法,总时间为0.000 6 s。所建立模型中各部件的尺寸信息、单元类型及各个部件单元个数如表3所示。
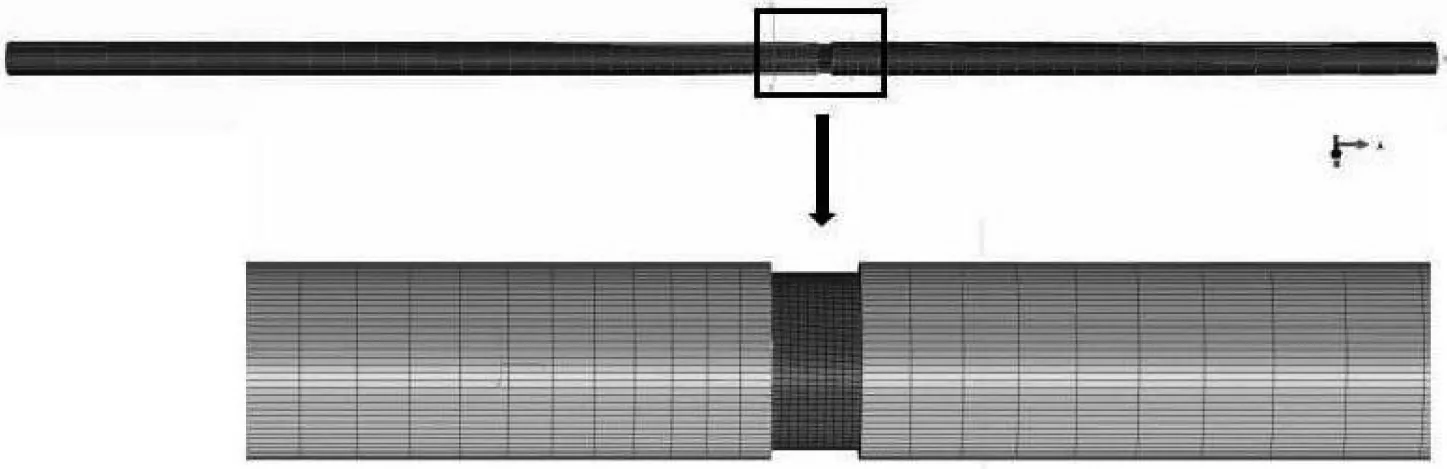
(a) SHPB有限元模型图

表3 模型各部件基本信息
由于在实际试验过程中,撞击杆(子弹)在整个试验过程中起到的作用为产生入射应力波,所以在有限元建模过程中省略了对撞击杆(子弹)的模拟,进而采用在实际试验过程中采集到的入射应力波,将其换算为力-时间曲线,作为均布荷载直接加载于入射杆的前端表面,典型的入射应力波如图15所示。

图15 SHPB入射波典型波形图
3.2 数值结果与分析
试件SF25-S0.6-60在210 s-1应变率冲击下的模拟破坏模态与实际试验破坏对比图,如图16所示。由图16可知,试件从边缘开始破坏,再逐步扩散至试件的中心,这与试验中得到的现象一致,试件的单元大多在320~500 μs内开始失效破坏,接着试件开始产生径向的膨胀,单元也逐渐开始剥离。

(a) t=200 μs
试件SF25-S0.6-60在210 s-1应变率下数值模拟应力应变曲线与试验应力应变曲线对比,如图17所示。由图17可知,数值模拟的应力应变曲线上升段及峰值应力与试验应力应变曲线吻合较好,而下降段应变的模拟与试验结果有一定的差异,主要是由于冲击试验的应力应变曲线下降段存在较大的离散型。总体而言,有限元分析结果与试验结果吻合较好,验证了结果的可靠性。

图17 试验与数值模拟应力应变曲线对比
4 钢纤维地质聚合物混凝土冲击应力-应变本构模型
钢纤维地质聚合物混凝土动态抗压应力-应变曲线关系采用过镇海[16]提出的分段式本构模型,如式(2)~式(4)所示。根据试验数据,通过数学手段进行统计回归,最终提出参数a,b、应变率θ与钢纤维体积掺量γ的关系如下
x=ε/εc
y=σ/fc
(2)
上升段
y=ax+(3-2a)x2+(a-2)x3
(3)
下降段
y=x/[b(x-1)x2+x]
(4)
式中:a=1+0.016 8θ;b=2e-0.35γ(1+0.001 2γ);fc=FDI-σ-σ·fc′,FDI-σ为应力动态增长因子,fc′为钢纤维地质聚合物混凝土棱柱体的静态轴心抗压强度;εc=FDI-ε-ε·εc′,FDI-ε为应变动态增长因子,εc′为峰值应变;θ为应变率;γ为钢纤维体积掺量。
为验证该冲击应力-应变本构模型的准确性,计算获得不同基准强度的钢纤维地质聚合物混凝土的应力-应变曲线,并与试验结果进行对比,结果如图18所示。由图18可知,本构计算曲线与试验曲线总体吻合良好,可预测冲击荷载下钢纤维地质聚合物混凝土的力学性能。
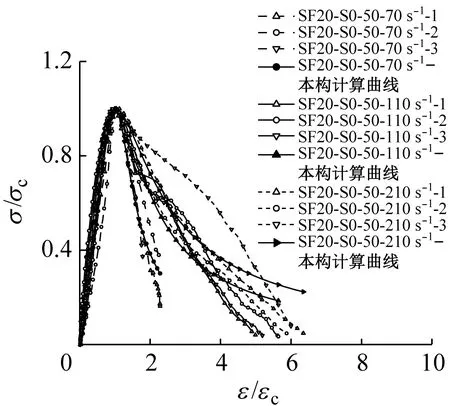
(a) SF20-S0-50
5 结 论
通过SHPB对不同冲击气压(对应不同应变率)、不同体积钢纤维掺量的地质聚合物混凝土进行抗冲击性能试验研究,得出以下结论:
(1) 钢纤维地质聚合物混凝土的动态抗压强度随着应变率、混凝土基准强度的提高逐渐增大,而钢纤维掺量仅对强度较低的地质聚合物混凝土产生较大影响。
(2) 应变率的提高使试件完整性逐渐变差,而随着钢纤维掺量与混凝土基准强度的提高,试件完整性逐渐变好,冲击耗能与韧性逐渐增加。
(3) 采用的SHPB有限元分析方法,计算结果与试验吻合较好,验证了结果的可靠性,同时还能为SHPB冲击试验的分析提供参考。
(4) 建立了钢纤维地质聚合物混凝土的抗冲击应力-应变曲线本构模型,本构计算结果与试验结果总体吻合较好,可预测冲击荷载下钢纤维地质聚合物混凝土的力学性能。
