基于数学模式探析数学竞赛中的数列问题

湖南师范大学数学与统计学院(410081) 吴仁芳 张立京

数列问题在竞赛数学中占有重要地位,对其进行细致研究将极大地丰富竞赛数学的内容,更有助于推动竞赛数学的纵向发展.数列常常是设计数列综合题的“中途点”、命制竞赛试题的“增长点”、解答思路的“突破点”,而且也是许多国内竞赛题和国际竞赛题的“关键点”.解决数列问题通常需要借助开阔的思维方式,可以通过如观察试验、归纳猜想、类比联想、一般与特殊、数形结合等思维方法,尤其在解决递推数列问题时解题思路主要有归纳、迭代和构造[1],并且具有特殊解法如特征根法、数学归纳法、不动点法、母函数法等[2],同时数列问题解决也渗透了如观察、探索、枚举、化归等现代数学的思想、解题策略等.灵巧变换地求解数列问题能拓展学生的逻辑思维和逻辑抽象,提高学科学习能力,为未来专业发展奠定良好基础;同时,深刻剖析竞赛数学中的数列问题有利于挖掘其内在联系、丰富其发展概貌.本文基于竞赛试题和相关文献分析,整理出数列问题中的常用解法包含化归法、错位相减法、裂项求和法、错项相消法、待定系数法、数学归纳法、不动点法、换元法、特征根法、母函数法等,为后续模式结构的分类作铺垫.

郑毓信认为模式之于数学具有特殊意义,数学的本质即是关于数学模式的科学[3],喻平认为各种基本概念、理论体系、命题、方法都归属于数学模式[4],于文华认为模式是有层次性的,可以有基本的数学模式,也可以有几种基本模式的叠加组合,各模式之间关系呈网状结构[5].因此对于数学的研究应注重模式观念,善于从模式的角度去发现和理解数学问题,以发挥数学的本质特征作用.策略意指总体的行动方针,而解题策略是在探索问题答案时采取的途径和方法,本文结合任樟辉、罗增儒等教授提出的解题策略[6][7],即以简驭繁、进退互用、化生为熟、动静转换、分合相辅、引参求变、正难则反,拟以解题策略为分类依据对数列问题中所涉及的模式进行划分,整合数学竞赛中常用求解数列问题的方法,整理出12 种模式结构,分别为换元模式、特征根模式、母函数模式、数学归纳法模式、放缩模式、化归模式、韦达定理模式、不动点模式、配方模式、拆合模式、待定系数模式、反证法模式.

以简驭繁策略意指用简单的观点去看待复杂的形式以便抓住形式所表现的数学问题本质,本文表现为换元模式、特征根模式、母函数模式;进退互用策略意指运用以进求退、以退求进的辩证关系转换数学问题,如一般与特殊、抽象与具体、高维与低维、强命题与弱命题,本文表现为数学归纳法模式、放缩模式;化生为熟策略意指把陌生问题通过适当变形转为熟悉问题来求解,本文表现为化归模式、韦达定理模式;动静转换策略意指可用动的观点来处理静的特征,也可用静的方法来处理动的过程,本文表现为不动点模式;分合相辅策略意指可以将求解问题进行分割处理,也可以进行添项处理以使得问题变为合理易求,本文表现为配方模式、拆合模式;引参求变策略意指通过参数的加入使得问题中量的关系变得明晰以此找到求解路径,本文表现为待定系数模式;正难则反策略意指当使用直接解法不能求解时转用间接证法使问题得以顺利解决,本文表现为反证法模式.

1 借助以简驭繁策略,构造数学模式

1.1 换元模式换元模式是指以局部整体的思想对所求量的表现形式进行变换,通过对新变量的成功求解,从而求得原所求量,中间过程要留意前后量的取值变化.其模式识别过程为:当问题解决者面对问题时,首先将其归类为数列问题,观察问题的整体结构和局部特征为了简化变量抓住问题本质,与自身认知结构中的换元模式相匹配,经由解题正向迁移使得问题成功求解.

换元法是换元模式的典型方法,使用换元法求数列的通项公式的基本思路是:恰当选择变换函数φ(x),使φ(x)的值域包含数列{an}的值域,并令an=φ(bn),代入{an}的递推式an=f(an-1)中,经过化简整理得到{bn}的一个新的递推式bn=g(bn-1).如果从bn=g(bn-1)能求出{bn}的通项公式,则{an}的通项公式即为an=φ(bn).

评注本题中所给的递推式含有根号,导致解题者无法直接对问题形成正确表征.因此需要应用换元模式,将递推式进行有理化,降低其外在认知负荷.然后经过简单运算即可完成对问题的表征,进而完成问题与内在认知中的基本数列结构的匹配,从而正确求解.由此可见,换元模式可降低解题者的外在认知负荷,同时也能简化问题表现形式,突出问题本质特征,便于解题者迅速与内在认知中的基本结构进行匹配.

1.2 特征根模式特征根模式是指针对具有常系数齐次线性方程特征的递归数列,运用其特征根的独特性质对数列进行求解.其模式识别过程为:当问题解决者面对问题时,先将其归类为递归数列问题,分析题干整体特征为了明晰变量特征抓住本质,与自身认知结构中特征根模式相适配,经由思维正向迁移使得问题得以求解.

特征根法是特征根模式的典型操作方法,也是求常系数齐次线性递归数列通项的重要方法.对于k阶常系数齐次线性递归数列

评注本题通过观察题目信息,获取到了常系数齐次线性方程的有关特征,以特征根的方式求出数列通项公式,注意到本题需要用到两次特征根法.由此可见,相对于构造简单数列结构求解数列通项,特征根模式为解题者提供了更一般的思路和结构,降低了问题表征难度,达到以简驭繁的效果.尤其是在解决高阶递归数列问题时,利用特征根模式可迅速完成问题表征,进而完成求解.

1.3 母函数模式母函数模式是指针对当前问题形式联系级数的相关特征,运用母函数的有关性质来求解得到数列通项公式.其模式识别过程为:当问题解决者面对问题时,将其归类为数列问题,观察题干所给信息发现特征结构为了将问题有关方法转化为较简的形式,与自身认知结构中的母函数模式相匹配,然后经过解题正向迁移最终求解数列通项.

母函数法是母函数模式的典型方法,在求解k阶线性递推式的数列通项时,常用到母函数法.对于数列{an}把下面形式的级数f(x)=a0+a1x+a2x2+···+anxn+···视为其母函数,然后运用函数与级数的有关性质变换求得通项公式.

例3数列{an}满足an+2=4an+1-4an,a1=3,a2=8,求数列{an}的通项公式.

解析设数列{an}的母函数为

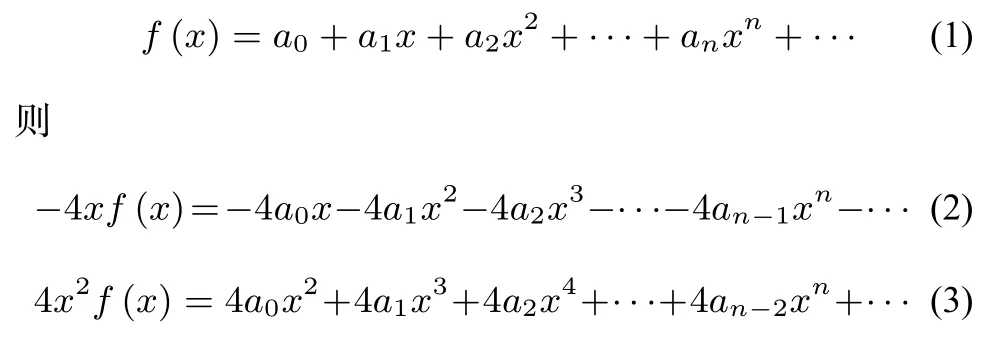
评注本题通过建立数列与母函数的对应关系,将问题简化后与解题者认知中的基本函数结构进行匹配,然后适配函数运算方法进行求解.由此可见,在应用母函数模式求解复杂数列问题时,只需通过函数之间的运算变形以及级数性质即可完成求解,因此母函数模式能大幅度减少解题者的思维量,让其能快速完成问题表征.

2 借助进退互用策略,构造数学模式

2.1 数学归纳法模式数学归纳法模式是指在发现某量之间的规律关系后,通过数学归纳法的固定步骤从特殊推往一般对问题进行证明求解.其模式识别过程为:当问题解决者面对问题时,归类为数列问题,观察题目信息发现特有规律为了以退求进实现从特殊到一般,与自身认知经验中的数学归纳法模式相匹配,经由正向迁移求解所给问题.

数学归纳法是数学归纳法模式的操作方法,利用数学归纳法求通项一般是通过计算找出数列前若干项的规律,给出通项的表达式的猜想,再由数学归纳法加以证明.

评注本题涉及数列{an},{bn}和实数A,B多个量,直接求解十分困难.故采取以退求进策略,先运用降维法将问题转化为证明只含数列{ki}与A的不等式,进而发现其规律,然后再结合数学归纳法问题即可迎刃而解.由此可见,数学归纳法模式可降低问题的表征复杂度,引导解题者明确规律关系,进而对问题进行方法适配,完成求解.

2.2 放缩模式放缩模式是指通过对某变量进行放大或缩小操作使得该变量特殊化、具体化,以便更易求解问题.其模式识别过程为:当问题解决者面对问题时,归类为数列问题,由题目信息发现不等式的有关特征,为了增强命题特征实现从一般到特殊,与自身认知经验中的放缩模式相匹配,经由解题迁移成功求解问题.

放缩法是放缩模式的操作方法.在数列不等式的证明过程中,要证明不等式A ＜B成立,有时可以将它的一边放大或缩小,寻找一个中间量,如将A放大成C,即A ＜C,后证C ＜B.放缩法在不等式型的证明中十分常见,关键是要对放缩尺度进行灵活把控.

例5(2012 年国际奥林匹克数学竞赛第二题) 设整数n≥3,正实数a2,a3,···,an满足a2a3···an=1.证明:(1+a2)2(1+a3)3···(1+an)n ＞nn.

解析利用均值不等式进行放缩,有

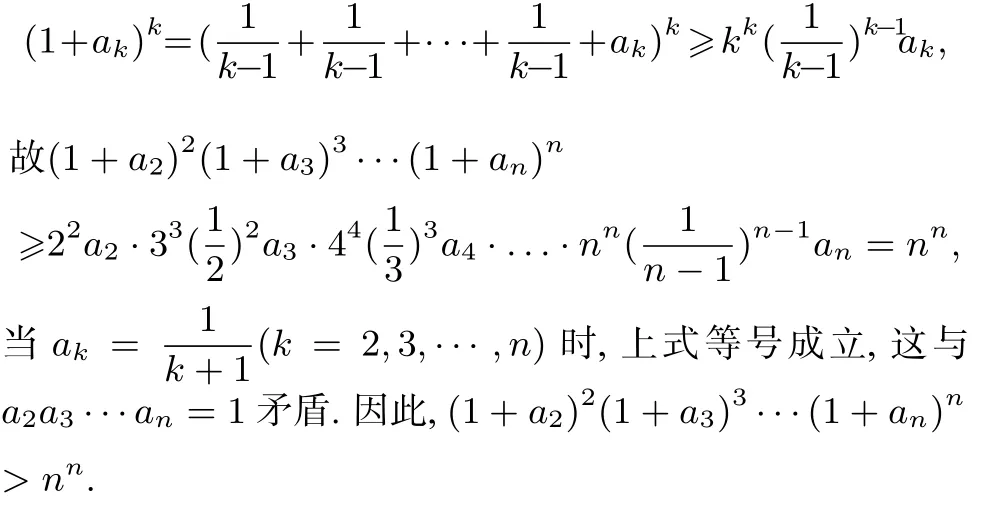
评注通过观察本题所证不等式的特征,可发现不等式左边是数列{(1+ak)k}各项的乘积,故可根据数列自身特征构造中间量(即运用均值不等式进行放缩)逐步逼近目标,然后再根据题设条件调整放缩尺度即可完成证明.由此可见,若将问题解决视为条件与结论之间因果关系的演绎,那么放缩模式可为解题者提供逼近目标的方向,同时结合进退互用策略可合理把握放缩尺度,进而完成问题证明.

3 借助化生为熟策略,构造数学模式

3.1 化归模式化归模式是指将未曾见过的特殊数列进行变形转化成为已学的等差数列、等比数列、常数列等来求解通项.其模式识别过程为:当问题解决者面对问题时,归类为数列问题,观察题目所给关系特征为了化难为易,与自身认知经验中的化归模式相匹配,经由解题迁移求解所给问题.

化归法是化归模式的操作方法,也是化归思想的主要方法,等差、等比数列的求和公式是基本知识,在遇到一些特殊数列的求和问题时,往往可以将这些特殊数列转化为等差、等比数列,再依据公式和已有的知识和条件进行求解.

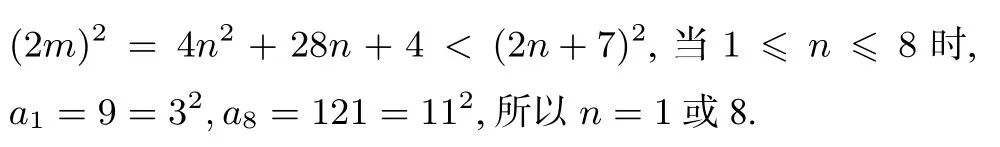
评注化归模式实质上是通过对特殊数列进行变形与构造,进而与解题者认知中的基本结构(如数列的线性关系结构)进行匹配,进而完成对问题表征.例如本题就通过对递推式an+1=进行了一系列的变形与构造,将其转化为一个常数列结构,使得问题得以解决.

3.2 韦达定理模式韦达定理模式是指针对具有一元二次方程型特征的式子对其运用根与系数的关系求解数列通项.其模式识别过程为:当问题解决者面对问题时,归类为数列问题,分析题目关系特征为了简易求解,与自身认知经验中的韦达定理模式相匹配,经由解题迁移求解所给问题.

韦达定理法是韦达定理模式的操作方法,主要是运用一元二次方程中根与系数的性质来求解问题.

评注由于数列是特殊的函数,而函数通常与方程相关联,因此在分析数列问题时可考虑从方程角度对其递推式进行表征.韦达定理模式实质上是从方程角度对数列递推式进行表征,从而与解题者认知中的韦达定理结构进行匹配,进而利用韦达定理对数列通项进行求解.如本题依据数列所给的条件,整理出方程结构特征,然后利用韦达定理找出数列的递推关系,从而解决数列中项的整数属性.

4 借助动静转换策略,构造数学模式

4.1 不动点模式不动点模式是指明确某一固定不动点,依据该点的特殊性对问题进行变形求解.其模式识别过程为:当问题解决者面对问题时,将其归类为数列问题,观察问题发现存在不动点,为了发挥静的特征作用,与自身认知经验中的不动点模式相匹配,经由解题正向迁移求得数列通项.

不动点法是定点模式的常用方法,其主要用来求形如数列an=f(an-1)(n ∈N*)的通项公式,求解过程相当于是求函数f(x)的n次迭代.

评注本题的递推公式属于不动点法中的类型,通过公式求得两个不动点,并将原式变形,得到新的数列把{bn},由于数列{bn}的性质相对明显,求得其递推公式后再带回到原数列{an},得到其通项公式.由此可见,不动点模式利用数列是特殊函数这一性质,通过不动点对数列进行构造,将问题结构转化为解题者已有认知的基本数列结构或具有明显规律的数列结构,进而顺利完成求解.

5 借助分合相辅策略,构造数学模式

5.1 配方模式配方模式是指通过添加量或式子使得变量的关系变得特殊具体,更易求解问题.其模式识别过程为:当问题解决者面对问题时,归类为数列问题,观察题目信息发现特征为了使问题更清晰明朗,与自身认知结构中的配方模式相匹配,经由解题正向迁移成功求解问题.

配方法是配方模式的操作方法,一般来说对于等差数列中的最值问题,可以考虑用配方法来解决,将隐藏的关系挖掘出来.

评注本题条件中含二次形式,而目标是求最值,解题者经过整体分析后即可与认知结构中的配方模式进行匹配,然后分别对条件和结论进行分析,进而形成合理的问题表征,并适配配方法完成求解.由此可见,配方模式应用过程先利用整体分析完成模式配对,然后分别处理条件和结论进行方法适配,两者相辅相成,进而促进解题者形成准确的表征.

5.2 拆合模式拆合模式是指通过将式子进行拆分或整合操作,以达到某种规律性的问题变形,从而使得问题易求.该种模式体现分解与组合的数学思想.其模式识别过程为:当问题解决者面对问题时,将其归类为数列问题,通过分析所给特征信息为了拆分式子发现规律,与自身认知经验中的拆合模式相匹配,经由正向迁移求解所给问题.拆合模式在数列问题中常用的操作方法有错位相减法、裂项求和法、错项相消法.

5.2.1 错位相减法错位相减法在数列求和的问题中被广泛应用,对于一个等差数列和一个等比数列的对应项相乘构成的数列,往往可以运用错位相减法求和.

例10(1990 年全国高中数学联赛题)n2(n≥4)个正数排列n行n列:

评注本题先从局部入手,利用基本数列性质,求出行数列和列数量的特征量,然后整体分析得出目标数列表达式,进而与错位相减法进行适配,完成求和.由此可见,基于错位相减法的拆合模式本质是多次运用分合策略,降低解题者认知负荷,并逐步寻求正确的表征途径,进而完成问题表征与求解.

5.2.2 裂项求和法裂项求和法即把一个数列的通项分成两项差的形式,在求和的过程中消去中间项,只剩下有限项,在运用的过程中将数列每项分解再重新组合,消去一些项达到最终求和.

5.2.3 错项相消法错项相消法主要用来求有关和式的递归式的通项公式.

评注基于错项相消法的拆合模式主要是通过整体分析递推公式,消去中间量,得出目标的规律表达式,进而完成问题表征.本题将已知条件进行分析,通过错项相消得到含奇偶项规律的递归式,从而求解数列.

6 借助引参求变策略,构造数学模式

6.1 待定系数模式待定系数模式是指通过引入特定参数形成具体表达式,运用表达性特有性质进行问题求解.其模式识别过程为:当问题解决者面对问题时,归类为数列问题,依据题目所给信息为了连接题中变量关系,与自身认知结构中的待定系数模式相匹配,经由解题迁移求解数列通项.

待定系数法是待定系数模式的操作方法,常用来解决一些特殊数列的通项问题.

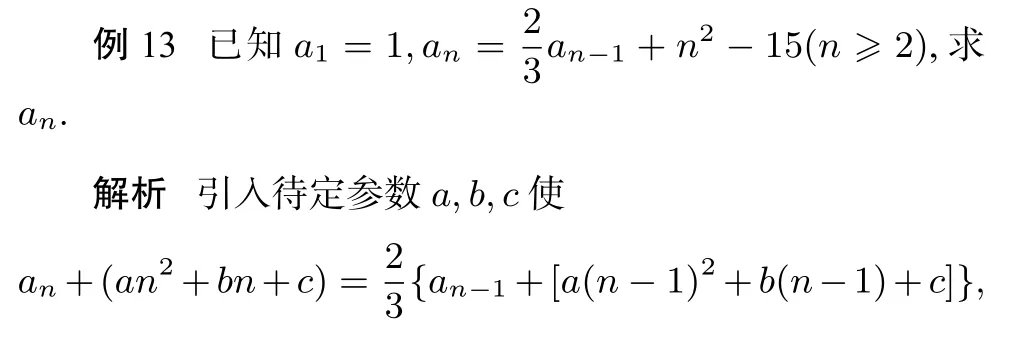
评注待定系数模式实质上是从解题者认知中的基本数列结构出发,通过类比其结构特征,引入参数将试题结构转化为与基本数列结构一致或相似的结构,进而完成问题求解.如本题通过引入参数,类比构造出等比数列的结构,使得变量间关系明确,从而求得结果.

7 借助正难则反策略,构造数学模式

7.1 反证法模式反证法模式是指对于不易直接求解的问题采用间接证法,以反证的方式推出矛盾从而求解问题.其模式识别过程为:当问题解决者面对问题时,归类为数列问题,观察题目信息为了简易求解,与自身认知经验中的反证法模式相匹配,经由解题迁移成功求解所给问题.反证法是极具特殊性的操作方法,常用于不易正向求解的数学问题.

例14(2002 年中国西部数学奥林匹克) 设S={a1,a2,···,an}是一个由0,1 组成的满足下述条件的最长数列:数列S中任意两个连续的5 项不同,即对任意1 ≤i ＜j ＜n-4,

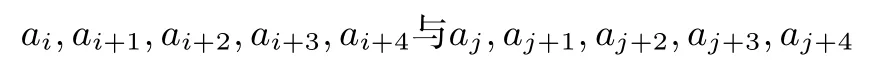
互不相同,证明:数列S最前面的4 项与最后面的4 项相同.

证明根据要证的结论的特点,考虑用反证法.若S最前面的4 项与最后面的4 项不相同,设S的最后4项为abcd,由于S为最长的具有题中性质的数列,从而在S后添加0 或1 后,所形成的5 数段abcd0 和abcd1必在S中出现,否则,新数列满足题中性质的数列与S={a1,a2,···,an}是最长的数列矛盾.即存在i/=j,i,j ∈{2,3,···,n-4},使得aiai+1ai+2ai+3ai+4=abcd0,ajaj+1aj+2aj+3aj+4=abcd1.

考虑ai-1,aj-1,an-4这三个数,其中必有2 个数相同:若ai-1=aj-1,则ai-1aiai+1ai+2ai+3=aj-1ajaj+1aj+2aj+3,从而,S中有2 个相同的5 数段,矛盾;若ai-1=an-4,则ai-1aiai+1ai+2ai+3=xabcd,而an-4an-3an-2an-1an=xabcd,矛盾;若aj-1=an-4,同理可以推出矛盾;命题得证.

评注分析题干发现本题利用已有条件难以直接对问题形成合适的表征,结合正难则反策略,与反证法模式进行匹配,再利用反证法即可完成证明.由此可见,反证法模式在解决特殊数列的证明问题时,可直接从方法角度完成对问题的表征,并且根据数列自身的规律性,可降低解题者的外在认知负荷,进而准确完成问题解决.

8 结语

数列问题是数学竞赛中的热点题型之一,试题难度一般较大,对于学生能力的考查较为综合.基于本文的分析与整理可以看出,在面对数学中比较难的题目时,学生要想正确而快速的解决问题,除了要具备深厚的数学知识以外还应具备多种能力,一是阅读理解能力,二是数学探究能力,三是应用能力,四是学习能力.其中,阅读理解能力即“读题”,要求学生读懂数学题目所讲的内容,最主要是挖掘出题目中的隐含条件;数学探究能力即“想题”,学生联想自己过去的解题经验,在已有认知结构中探寻解题思路;应用能力即“做题”,能将已有解题经验正向迁移到新环境中;学习能力即“思题”,能对一种新颖奇巧的解法或过程进行积极思考、主动学习来获取相关经验.对于数列问题的学习与思考应注重模式思想,体味模式解题的通达与简捷,如求公差、公比、首项、项数时的基本量模式思想,方程模式思想,巧用设而不求的方法进行整体代换的模式思想等.