美国数学月刊12214 题引发的探究

华南师范大学数学科学院(510631) 叶秀锦

贵州省毕节市七星关区第五实验学校(551700) 臧军

1 问题背景

原题(《美国数学月刊》12214 题[1]) 设x,y,z是三角形ABC三条中线的长度,三角形ABC的面积为S′.证明:

2 预备知识

引理1设D,E,F是三角形ABC三边BC,AC,AB的中点,三角形ABC的面积为S′,那么AD,BE,CF三边的长度可以构成三角形,并且这个新三角形的面积为

证明如图1 所示.连结AD,BE,CF,AD,BE,CF相交于I.延长FE到G,使得EG=FE,连结AG,CG.连结DG交AC于H.

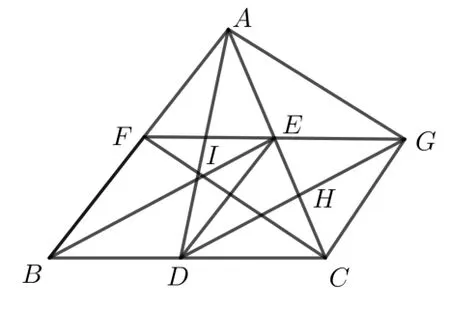
图1

引理2已知a,b,c都是正数,令p=a+b+c,q=ab+ac+bc,t=abc,那么有:(1)p2≥3q;(2)q2≥3pt;(3)pq≥9t;(4)p3≥27t;(5)p3-4pq+9t≥0.

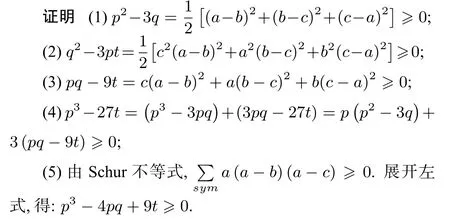
3 等价问题与加强问题

由引理1,可知x,y,z三边的长度可构成一面积为S的三角形,S=不难将原问题转化为如下的等价命题:

4 命题2 的两种证明

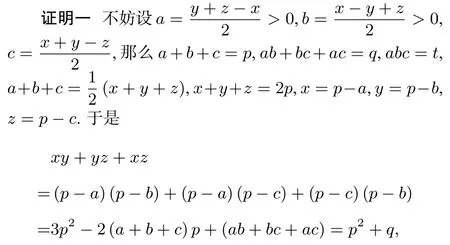
评注方法一通过代换转化为三元对称不等式问题,从而可以用上许多证明三元对称不等式的手段,是一种证明对称三角不等式的通法,易于证明比较强的结果,但对于证明一些比较弱的结果会显得比较复杂.方法二由于Gerretsen不等式的局限性,不适用于证明一些较强的结果,但对于证明一些比较弱的结果会显得比较方便.